高中物理机械波中的常见问题归纳例析专题辅导

机械波一、知识网络二、画龙点睛概念1、机械波(1)机械波：机械振动在介质中的传播，形成机械波。

(2)机械波的产生条件：①波源：引起介质振动的质点或物体②介质：传播机械振动的物质(3)机械波形成的原因：是介质内部各质点间存在着相互作用的弹力，各质点依次被带动。

(4)机械波的特点和实质①机械波的传播特点a．前面的质点领先，后面的质点紧跟；b．介质中各质点只在各自平衡位置附近做机械振动，并不沿波的方向发生迁移；c．波中各质点振动的频率都相同；d．振动是波动的形成原因，波动是振动的传播；e．在均匀介质中波是匀速传播的。

②机械波的实质a．传播振动的一种形式；b．传递能量的一种方式。

(5)机械波的基本类型：横波和纵波①横波：质点的振动方向跟波的传播方向垂直的波，叫做横波。

表现形式：其中凸起部分的最高点叫波峰，凹下部分的最低点叫波谷。

横波表现为凹凸相间的波形。

实例：沿绳传播的波、迎风飘扬的红旗等为横波。

②纵波：质点的振动方向跟波的传播方向在同一直线上的波，叫做纵波。

表现形式其中质点分布较稀的部分叫疏部，质点分布较密的部分叫密部。

纵波表现为疏密相间的波形。

实例：沿弹簧传播的波、声波等为纵波。

2、波的图象(1)波的图象的建立①横坐标轴和纵坐标轴的含意义横坐标x表示在波的传播方向上各个质点的平衡位置；纵坐标y 表示某一时刻各个质点偏离平衡位置的位移。

从形式上区分振动图象和波动图象，就看横坐标。

②图象的建立：在xOy坐标平面上，画出各个质点的平衡位置x 与各个质点偏离平衡位置的位移y的各个点(x，y)，并把这些点连成曲线，就得到某一时刻的波的图象。

(2)波的图象的特点①横波的图象特点横波的图象的形状和波在传播过程中介质中各质点某时刻的分布形状相似。

波形中的波峰也就是图象中的位移正向最大值，波谷即为图象中位移负向最大值。

波形中通过平衡位置的质点在图象中也恰处于平衡位置。

在横波的情况下，振动质点在某一时刻所在的位置连成的一条曲线，就是波的图象，能直观地表示出波形。

机械振动和机械波的几个相关问题内容提要：机械振动和机械波的问题是中学物理、普通物理、高能物理的重要内容之一，是高考的热点内容。

要使中学生比较深刻理解有关内容，牢固掌握它们两者的规律，就要对机械振动和机械波中的几个重点问题，有一个全面清晰的认识，掌握其处理方法。

现就这部分内容中出现的问题进行剖析，有利于同学们掌握该知识。

一、波的形成与传播过程中的问题物质（除场外）都是由分子组成的，分子之间有相互作用的引力和斥力。

如果物质中某一区域的分子从外界获得能量振动，那么这一区域的分子会通过分子之间的相互作用力带动周围的分子振动，这样，振动就会沿着物质由近及远的在物质中传播，同时波源的能量也随着波的传播而向周围的空间辐射。

所以，机械波既是波源的振动在物质中的传播，同时也是波源的能量在物质中的辐射。

由于机械波是波源的振动在物质中的传播，所以物质中的质点并不随波在物质中的传播而发生迁移。

传播的只是振动方式和能量。

由于机械波是依靠分子之间的相互作用力在物质中传播的振动，所以物质中任何一个质点的振动总是落后于波源的振动，任何一个质点的起振方向总是与波源的起振方向相同。

在物质中沿着波的传播方向总存在作振动情况（包括位移、速度、加速度）完全相同的点，相邻的这样两个点的距离叫波长。

相距整数个波长的两点振动情况总完全相同，相距半波长奇数倍的两点振动情况总是相反。

这就是振动和波的明显特征——周期性。

波在物质中的传播速度可用公式V ＝λf ＝λ/T计算，其中f 是质点的振动频率，由波源决定，V 是传播速度，由介质的物理特性决定，因为，λ=VT，所以波在一个周期内传播的距离等于一个波长。

波长λ由波源的振动频率和物质的物理特性共同决定。

因为，波在一个周期内沿传播方向传播一个波长的距离，所以，沿波的传播方向，波形也平移一个波长的距离。

【例1】如图-1所示，波源S 从平衡位置y=0开始振动，运动方向竖直向上（y 轴的正方向）振动周期T ＝0.01S ，同时产生向左、向右两个方向传播的简谐波，波速均为V ＝80m/s。

机械波多解问题归类分析机械波的多解问题历来是高考中的热门考点，无论是全国卷，还是上海卷，都屡屡出现。

同时本考点又是学生学习机械波时的难点所在。

其主要表现在无法正确判断多解问题的原因，从而造成错解。

本文将就机械波多解问题的源头──产生原因作简要的探讨，并结合最近几年高考中出现的考题说明对应的解题策略。

1 传播方向导致的多解问题波源起振后产生的波可以在介质中向四周传播。

若题中没有特别注明传播方向，则求解时必须讨论其传播方向，从而导致了波的多解问题。

例1（1987年全国高考题）如图所示，绳中有一列正弦横波，沿x轴传播，，b是绳上两点，它们在x轴上的距离小于一个波长，当点振动到最高点时，b点恰好经过平衡位置向上运动。

试在图上、b之间画出波形图。

分析：本题没有注明波的传播方向，所以需要对波向＋x轴，－x轴方向传播讨论。

由于、b间距离小于一个波长。

因此、b间不足一个波长，其图像如图乙所示，（1）为波向＋x轴传播时的波形；（2）是波沿－x轴传播时的波形。

2 波长大小导致的多解问题因题中没有给定波长的确切条件，故引起答案的不确定性导致多解问题。

例2 （1996年全国卷）如图甲所示，一根张紧的水平弹性长绳上的、b两点，相距14．0m。

b点在点右方，当一列简谐波沿此绳向右传播时，若点位移达到正向极大时，b点位移恰好为零，且向下运动。

经过1．00s后，点位移为零，且向下运动，而b点的位移恰好达到负向极大，则这列简谐波的波速可能等于：A．4．67m／s B．6m／s C．10m／s Ｄ．14m／s分析：此题虽然已说明了波的传播方向，但满足题设条件的、b两点可以有无数个可能位置，图乙中的b1、b2、b3……等。

只可以写出、b间距的通式；（n＝0、1、2……）。

从而波速的答案也是系列解答，经求解可知A、C为正确答案。

3 波形周期导致的多解问题简谐机械波是周期性的，每经过一个周期波形与原波形重复，从而导致了问题的多解性。

例3（1996年上海卷）一列横波在某时刻的波形图如图中实线所示，经0．02s后波形如图中虚线所示，则该波的波速和频率f可能是（）A．＝5m／s B．＝45m／s C．f＝50Hz D．f＝37．5Hz分析：此题波的传播方向不确定，需分向＋x轴和向－x轴传播两种情况讨论。

专题47机械波考点一波的形成及传播(1-2T)考点二波动图像(3-13T)考点三波动图像与振动图像的综合应用(14-20T)考点四波传播的周期性与多解性问题(21-28T)考点五波特有的现象：波的干涉、衍射多普勒效应(29-36T)考点一波的形成及传播1.机械波的形成条件：①有波源．②有介质．2.波的形成：波源的振动带动相邻的质点开始振动，这个质点又带动更远一些的质点，这样依次带动下去使后振动的质点依次重复前面质点的振动，从而在介质中形成机械波．由于每一个质点都在重复波源的振动所以每一个质点的起振方向都与波源起振方向相同．3.机械波向前传播的是振动这种运动形式，各质点只在各自的平衡位置附近振动，并不随波迁移．4.横波：质点的振动方向与波的传播方向相互垂直的波，横波有波峰和波谷．5.纵波：质点的振动方向与波的传播方向在同一直线上的波，纵波有密部和疏部．1．(多选)关于波的形成和特点，下列说法正确的是()A．随着波的传播，介质中各质点都在各自的平衡位置附近振动B．随着波的传播，介质中的各质点也将由近及远地迁移出去C．传播波的过程中相邻各质点间必有相互作用力D．某一横波在介质中沿水平方向传播，介质中的质点必沿竖直方向上下振动【答案】AC【解析】随着波的传播，介质中各质点都在各自的平衡位置附近来回振动，不随波迁移，故A正确，B错误；波源的振动使质点一个个被带动，且与波源振动形式相同，且总滞后于前一个质点，可知各质点间有力的作用，故C正确；某一横波在介质中沿水平方向传播，介质中的质点的振动方向与波的传播方向垂直，但不一定沿竖直方向，故D错误．2.关于横波和纵波，下列说法正确的是()A．对于横波和纵波，质点的振动方向和波的传播方向有时相同，有时相反B．对于纵波，质点的振动方向与波的传播方向一定相同C．形成纵波的质点随波一起迁移D．空气介质中只能传播纵波【答案】D【解析】横波中质点的振动方向与波的传播方向相互垂直，纵波中质点的振动方向总是与波的传播方向在同一直线上，有时相同，有时相反，故选项A、B 错误；无论是横波还是纵波，质点都是在平衡位置附近做往复运动，不会随波迁移，故选项C 错误；因为空气介质只能通过压缩而产生相互作用力，故空气介质中只能传播纵波，故选项D 正确．考点二波动图像1.波动图像表示在波的传播方向上，某一时刻各质点离开平衡位置的位移。

高中物理机械波分析题解析在高中物理学习中，机械波是一个重要的内容，也是考试中常见的题型。

本文将针对机械波的分析题进行解析，帮助高中学生和他们的父母更好地理解和应对这类题目。

一、题型分析机械波的分析题通常要求学生根据给定的条件，对波的性质、传播规律或其他相关内容进行推断和分析。

这类题目需要学生对机械波的基本概念和公式有一定的掌握，并能够运用所学知识解决实际问题。

二、解题思路解答机械波分析题的关键在于理清题目要求，运用所学知识进行推理和分析。

下面以几个具体的题目为例，介绍解题思路和方法。

1. 题目：一根长为1.5米的细绳，一端固定在墙上，另一端用手拿住并上下振动，当频率为30Hz时，在绳上沿着绳方向观察，相邻两个波峰之间的距离为0.5米。

求这根绳上的波速、波长和振动方向。

分析：根据题目给出的条件，我们可以得到频率f=30Hz，波峰间距d=0.5m。

首先，我们可以求得波速v，根据公式v=fλ，其中λ为波长。

代入已知条件，可得v=30Hz×0.5m=15m/s。

接着，我们可以求得波长λ，即λ=d=0.5m。

最后，根据观察绳的振动方向，可以确定振动方向为沿着绳的方向。

2. 题目：一根长为2米的弦上产生了频率为100Hz的驻波，波节间的距离为0.5米。

求弦上的波速、波长和频率。

分析：根据题目给出的条件，我们可以得到波节间距d=0.5m，频率f=100Hz。

首先，我们可以求得波速v，根据公式v=2fd，其中f为频率，d为波节间距。

代入已知条件，可得v=2×100Hz×0.5m=100m/s。

接着，我们可以求得波长λ，即λ=2d=1m。

最后，根据波速和波长的关系，可以求得频率f，即f=v/λ=100m/s/1m=100Hz。

三、解题技巧1. 理清题目要求：在解答机械波分析题时，首先要仔细阅读题目，理清题目要求和给出的条件。

只有明确了题目要求，才能有针对性地运用所学知识解答问题。

2. 运用公式：机械波分析题通常需要运用公式进行计算。

机械波多解问题归类分析1 传播方向导致的多解问题波源起振后产生的波可以在介质中向四周传播。

若题中没有特别注明传播方向，则求解时必须讨论其传播方向，从而导致了波的多解问题.例1如图所示,绳中有一列正弦横波，沿x轴传播，，b是绳上两点，它们在x轴上的距离小于一个波长，当点振动到最高点时，b点恰好经过平衡位置向上运动。

试在图上、b之间画出波形图。

2 波长大小导致的多解问题因题中没有给定波长的确切条件，故引起答案的不确定性导致多解问题.例2 如图甲所示,一根张紧的水平弹性长绳上的、b两点，相距14．0m。

b点在点右方，当一列简谐波沿此绳向右传播时，若点位移达到正向极大时，b点位移恰好为零，且向下运动。

经过1．00s后，点位移为零,且向下运动，而b点的位移恰好达到负向极大,则这列简谐波的波速可能等于：A．4．67m／s B．6m／s C．10m／s Ｄ．14m／s3 波形周期导致的多解问题简谐机械波是周期性的，每经过一个周期波形与原波形重复，从而导致了问题的多解性。

例3一列横波在某时刻的波形图如图中实线所示，经0．02s后波形如图中虚线所示,则该波的波速和频率f可能是（)A．＝5m／s B．＝45m／s C．f＝50Hz D．f＝37．5Hz4 质点振动方向导致的多解问题例4 一列简谐横波向右传播,波速为,沿波传播方向上有相距为的P、Q两质点，如图所示，某时刻P、Q两点都处于平衡位置,且P、Q间仅有一个波峰，经过时间t,Q质点第一次运动到波谷，则t的可能值有( ）A．1个B．2个C．3个D．4个5 传播时间导致的多解问题题目中所给定的时间条件不充分,可能比一个周期长，可能比一个周期短，从而导致了多解问题的出现.例5 一列横波在x轴上传播，t1＝0和t2＝0．005s时刻的波形分别如图中实线和虚线所示。

（1）求这列波的波速;(2）若波速为6000m／s，求波的传播方向.6 质点振动图像导致的多解问题例6 一列沿＋x轴传播的简谐波，在x1＝10cm和x2＝110cm处的两点振动图线分别如图中实线和虚线所示，试求质点振动周期和简谐波的波长。

关于机械波多解问题的例析山东临沂双月园学校（276017）刘忠涛机械波多解问题历来是各级各类考试中经常考察的热点，也是高中物理教学中的一个重点和难点。

学生在求解机械波问题时，往往由于对波动的实质理解不深刻、对题目中隐含条件挖掘不透彻、对已知条件使用不全面等，常常会出现解答不完整而造成漏解。

本文限于横波沿一条直线传播的情形，就常见的机械波多解问题通过剖析其成因进行归类例析，力求帮助学生掌握解决此类问题的根本。

一、波传播的“双向性”带来的多解问题机械波在同种介质中沿一条直线传播的情形下，波的传播方向有两种可能，这就是波传播的“双向性”。

当题目没有明确波的传播方向时，我们必须要考虑波传播的“双向性”，才能得出完整的答案。

例1如图1所示，一列简谐横波以速率v传播，t1时刻的波形为实线，t2时刻的波形为虚线。

已知△t= t2- t1=0.06s，且△t小于一个周期T。

则下列关于该列波传播的周期与速率的判断，可能正确的是( )。

A．T=0.24s，v=50m／sB．T=0.08s，v=150m／sC．T=0.24s，v=150m／sD．T=0.08s，v=50m／s解析：本题没有明确波的传播方向，因此需要考虑波传播的“双向性”。

由图1可知，该波的波长为λ=12m。

（1）若波沿+x方向传播，由图1可看出，波在△t内传播的最小距离为△S=λ／4。

又则波速大小v=△s／△t=λ／T =50m ／s.（2）若波沿－x 方向传播，同理可得另一组解T=0.08s ，v=150m ／s.故本题正确选项为A 、B 。

二、波传播的周期性带来的多解问题机械波在介质中传播的过程中，由于介质质点做周期性的振动，因而波的图像也具有周期性。

这种周期性表现在两个方面：时间上的周期性和空间上的周期性。

（一）波传播的时间上的周期性产生多解设某简谐波周期为T ，传播过程中在时刻t 各振动质点形成一波形，经过时间△t＝nT （n=0，1，2，3，……）各振动质点又回到t 时刻的位置。

高中物理波动机械波题详解波动是高中物理中一个重要的概念，涉及到机械波的传播和特性。

在考试中，波动题目常常是难倒学生的难题。

本文将详细解析几道典型的机械波题目，帮助学生理解波动的基本原理和解题技巧。

题目一：一根绳子上的横波传播速度为10m/s，频率为50Hz。

求波长。

解析：根据波动的基本公式v = λf，其中v为波速，λ为波长，f为频率。

已知v = 10m/s，f = 50Hz，代入公式可得λ = v/f = 10/50 = 0.2m。

因此，波长为0.2m。

这道题考察了波动的基本公式的应用，需要学生掌握波动的基本概念和公式，并能够根据已知条件求解未知量。

题目二：一根绳子上的纵波传播速度为20m/s，频率为100Hz。

求波长。

解析：与题目一类似，根据波动的基本公式v = λf，已知v = 20m/s，f = 100Hz，代入公式可得λ = v/f = 20/100 = 0.2m。

因此，波长为0.2m。

这道题同样考察了波动的基本公式的应用，但是与题目一不同的是，这里涉及到的是纵波的传播速度。

学生需要理解横波和纵波的区别，并能够根据已知条件求解未知量。

题目三：一根绳子上的横波传播速度为10m/s，频率为50Hz。

求波动的周期。

解析：根据波动的基本公式v = λf，已知v = 10m/s，f = 50Hz，代入公式可得λ = v/f = 10/50 = 0.2m。

因此，波长为0.2m。

波动的周期T与频率f的关系为T = 1/f，代入已知的f = 50Hz可得T = 1/50 = 0.02s。

因此，波动的周期为0.02s。

这道题目考察了波动的周期与频率的关系，学生需要理解波动的周期与频率的定义，并能够根据已知条件求解未知量。

通过以上三道题目的解析，我们可以看出，波动题目的解题思路基本相同，都是根据波动的基本公式进行计算。

关键是理解波动的基本概念和公式，并能够根据已知条件求解未知量。

在解题过程中，学生还需要注意单位的转换和计算的准确性。

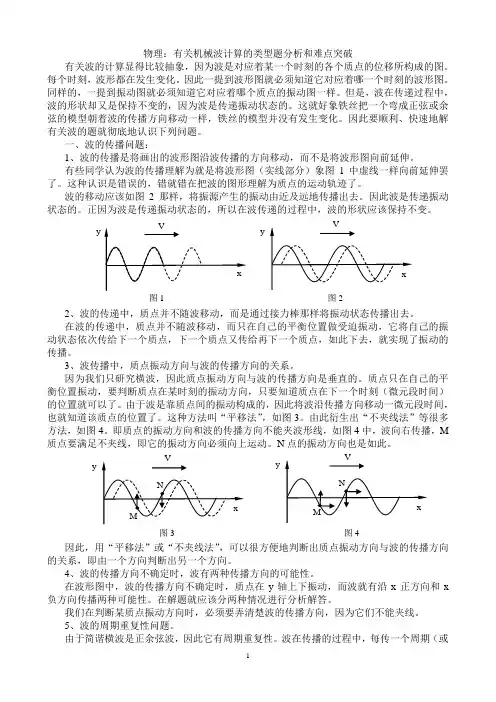
物理：有关机械波计算的类型题分析和难点突破有关波的计算显得比较抽象，因为波是对应着某一个时刻的各个质点的位移所构成的图。

每个时刻，波形都在发生变化。

因此一提到波形图就必须知道它对应着哪一个时刻的波形图。

同样的，一提到振动图就必须知道它对应着哪个质点的振动图一样。

但是，波在传递过程中，波的形状却又是保持不变的，因为波是传递振动状态的。

这就好象铁丝把一个弯成正弦或余弦的模型朝着波的传播方向移动一样，铁丝的模型并没有发生变化。

因此要顺利、快速地解有关波的题就彻底地认识下列问题。

一、波的传播问题：1、波的传播是将画出的波形图沿波传播的方向移动，而不是将波形图向前延伸。

有些同学认为波的传播理解为就是将波形图（实线部分）象图1中虚线一样向前延伸罢了。

这种认识是错误的，错就错在把波的图形理解为质点的运动轨迹了。

波的移动应该如图2那样，将振源产生的振动由近及远地传播出去。

因此波是传递振动状态的。

正因为波是传递振动状态的，所以在波传递的过程中，波的形状应该保持不变。

2、波的传递中，质点并不随波移动，而是通过接力棒那样将振动状态传播出去。

在波的传递中，质点并不随波移动，而只在自己的平衡位置做受迫振动，它将自己的振动状态依次传给下一个质点，下一个质点又传给再下一个质点，如此下去，就实现了振动的传播。

3、波传播中，质点振动方向与波的传播方向的关系。

因为我们只研究横波，因此质点振动方向与波的传播方向是垂直的。

质点只在自己的平衡位置振动，要判断质点在某时刻的振动方向，只要知道质点在下一个时刻（微元段时间）的位置就可以了。

由于波是靠质点间的振动构成的，因此将波沿传播方向移动一微元段时间，也就知道该质点的位置了。

这种方法叫“平移法”，如图3。

由此衍生出“不夹线法”等很多方法，如图4。

即质点的振动方向和波的传播方向不能夹波形线，如图4中，波向右传播，M 质点要满足不夹线，即它的振动方向必须向上运动。

N 点的振动方向也是如此。

因此，用“平移法”或“不夹线法”，可以很方便地判断出质点振动方向与波的传播方向的关系，即由一个方向判断出另一个方向。

高中物理机械波问题的解题技巧高中物理中，机械波是一个十分重要的概念，也是较为抽象和复杂的一部分内容。

掌握机械波问题的解题技巧，不仅对提高物理成绩和解题能力有着积极作用，而且对理解波动现象和应用具有重要意义。

本文将介绍几种常见的机械波问题，并解释相应的解题技巧。

一、波速和频率的关系机械波传播的速度称为波速，一般用v表示。

对于波速和频率的关系，可以通过以下公式计算：v = λf其中，λ表示波长，f表示频率。

根据公式，波长和频率之间成反比。

例如，某一波的频率为500Hz，波长为2m。

如果要求这一波在传播时的速度，可以使用上述公式进行计算：v = 2m × 500Hz = 1000m/s这一问题可通过公式计算得到波速。

二、超出开口处线宽的多普勒效应在介质中传播的波遇到开口时，波在开口处会出现衍射现象。

当波源接近开口时，波的波长会变短，频率增大，进而超出开口处线宽，这种现象称为多普勒效应。

解答此类问题时，可以使用以下公式：f ' = (v ± Vr) / (v ± Vs) × f其中，f '表示接收到的频率，v表示波速，Vr表示接收器相对于介质的速度，Vs表示波源相对于介质的速度，f表示波源的频率。

例如，一辆车以30m/s的速度向南行驶，它发出的声音频率为500Hz，求观察者在不同位置时接收到的频率。

首先，观察者向南行驶时，观察者速度Vr为正，波源速度Vs为零。

代入公式可得：f ' = (v + Vr) / (v + Vs) × f= (v + 30m/s) / v × 500Hz然后，在观察者远离波源的情况下，观察者速度Vr为负，波源速度Vs为零。

代入公式可得：f ' = (v - Vr) / (v - Vs) × f= (v - 30m/s) / v × 500Hz通过以上计算，我们可以得到观察者在不同位置时接收到的频率。

机械波一、波的形成和传播[考点1 机械波的形成和传播]1、如图所示为沿水平方向的介质中的部分质点,每相邻两质点的距离相等,其中O 为波源．设波源的振动周期为T,自波源通过平衡位置竖直向下振动时开始计时,经过T/4,质点1开始振动,则下列关于各质点的振动和介质中的波的说法中错误的是〔 B 〕A ．介质中所有质点的起振方向都是竖直向下的,且图中质点9起振最晚B ．图中所画出的质点起振时间都是相同的,起振的位置和起振的方向是不同的C ．图中质点8的振动完全重复质点7的振动,只是质点8振动时,通过平衡位置或最大位移的时间总比质点7通过相同位置时落后T/4D ．只要图中所有质点都已振动了,质点1与质点9的振动步调就完全一致,但如果质点1发生的是第100次振动,则质点9发生的就是第98次振动2、如图是某绳波形成过程的示意图,1、2、3、4……为绳上的一系列等间距的质点,绳处于水平方向.质点1在外力作用下沿竖直方向做简谐运动,带动2、3、4……各个质点依次上下振动,把振动从绳的左端传到右端.t =0时质点1开始竖直向上运动,经过四分之一周期,质点5开始运动.下列判断正确的是〔C 〕A ．质点6开始振动时的运动方向向下B ．2T t =时质点6的加速度方向向上 C ．43T t =时质点10的运动方向向上 D ．T t =时质点16开始运动[考点2 振动和波动的区别和联系]3、关于振动和波动的关系,下列说法正确的是〔 A 〕A 、振动是波的成因,波是振动的传播B 、振动是多个质点呈现的运动现象,波是许多质点联合起来呈现的运动现象C 、波的传播速度就是质点的振动速度D 、波源停止振动时,波立即停止传播4、关于质点的振动和波的传播,下列说法正确的是〔 C 〕A 、介质中的质点随波的传播而迁移B 、质点振动的方向总是垂直于波的传播方向C 、波不但传递能量,还能传递信息D 、一切波的传播均需要介质左 右1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 2 0 9二、波的图像[考点1 波图像的理解]5、如图所示是一列简谐横波某时刻t0的波形图,试根据波形图回答下列问题：〔1〕该时刻加速度最大的质点有哪些？〔2〕速度最大的质点有哪些？〔3〕振动方向相同的质点有哪些？这些点的分布有什么规律？〔4〕如果这列波沿x轴负方向传播,质点3受到合外力的方向如何？6、在均匀介质中有一个振源S,它以50H Z的频率上下振动,该振动以40m/s的速度沿弹性绳向左、右两边传播.开始时刻S的速度方向向下,试画出在t=0.03s时刻的波形.7.[13年高考]如图,t=0时刻,波源在坐标原点从平衡位置沿y轴正方向开始振动,S 振动周期为0.4s,在同一均匀介质中形成沿x轴正、负两方向传播的简谐横波.下图中能够正确表示t=0.6时波形的图是[ C ][考点2 振动图和波形图的综合应用]8.[12年高考]一列简谐波沿x轴传播,t=0时刻的波形如图甲所示,此时质点P正沿y轴负方向运动,其振动图像如图乙所示,则该波的传播方向和波速分别是[ A ]A．沿x轴负方向,60m/s B．沿x轴正方向,60m/sC．沿x轴负方向,30 m/s D．沿x轴正方向,30m/s9、如图所示为一列简谐横波在t = 0时刻的波形图,已知这列波沿x轴正方向传播,波速为20 m / s,P是离原点为2 m的一个质点,则t = 0.17 s时刻,质点P的运动情况是[ A ]A．速度和加速度都沿－y方向B．速度沿+y方向,加速度沿－y方向C．速度和加速度均在增大D．速度正在减小,加速度正在增大10、一列简谐横波沿x轴正向传播,传到M点时波形如图所示,再经0.6s,N点开始振动,则该波的振幅A和频率f [ D ]A．A=1m f=5HZ B．A=0.5m f=5HZC．A=1m f=2.5 HZ D．A=0.5m f=2.5 HZ11、一列波沿直线传播,在某一时刻的波形图如图所示,质点A的位置与坐标原点相距0.5 m,此时质点A沿y轴正方向运动,再经过0.02 s将第一次达到最大位移,由此无法判断[ B]A．这列波波长是2 mB．这列波频率是50 HzC．这列波波速是25 m/sD．这列波的传播方向是沿x轴的负方向12.一简谐横波在x 轴上传播,波源振动周期T =0.1 s,在某一时刻的波形如图所示,且此时a 点向下运动.则[ B ]A.波速为20 m/s,波沿x 轴正向传播B.波速为20 m/s,波沿x 轴负向传播C.波速为10 m/s,波沿x 轴负向传播D.波速为10 m/s,波沿x 轴正向传播三、波的多解问题[考点1 波的传播方向不确定性引起多解问题]13、[10年高考]一列简谐横波在t =0时刻的波形如图中的实线所示,t =0.02s 时刻的波形如图中虚线所示.若该波的周期T 大于0.02s,则该波的传播速度可能是[ ] A ．2m/s B ．3m/s C ．4m/s D ．5m/s14、横波如图所示,t 1时刻波形为图中实线所示；t 2时刻波形如图中虚线所示．已知Δt=t 2-t 1=0.5s,且3T ＜t 2-t 1＜4T,问：〔1〕如果波向右传播,波速多大？ 〔2〕如果波向左传播,波速多大？〔1〕如果波向右传播,则t 时间内传播了〔n+1/4〕T,即t=13/4T,T=4/13t 波长λ=4m 波速v=λ/T=26m/s〔2〕如果波向左传播,则t 时间内传播了〔n+3/4〕T,即t=15/4T,T=4/15t 波速v=λ/T=30m/s15、<10分>一列横波在x 轴方向传播,t 1=0时刻的波形图如图实线所示,t 2=0.5s 时刻的波形图如图虚线所示,已知波的周期大于0.5s,求这列波的波速.解：由Δt =0.5s ＜T,即ΔX ＜λ<1>如果波是向左传播的,从图可以看出虚线所示的波形相当于实线所示的波形向左移动了2m<1/4的波长>,则波速的大小V 1=ΔX /Δt=2/0.5<m/s>=4m/s<2> 如果波是向右传播的,从图可以看出虚线所示的波形相当于实线所示的波形向右移动了6m<3/4的波长>,则波速的大小V 2=ΔX /Δt=6/0.5<m/s>=12m/s[考点2 波的周期性形成多解问题]16、一列简谐横波沿直线传播,该直线上的a 、b 两点相距4.42 m.图中实、虚两条曲线分别表示平衡位置在a 、b 两点处质点的振动曲线.从图示可知[ C ]A ．此列波的频率可能是10HzOy /cmx /cm481216 t =0t =0.02s2-2x/mx/mB ．此列波的波长一定是0.1mC ．此列波的传播速度可能是34 m/sD ．a 点一定比b 点距波源近17.一列简谐横波沿直线由a 向b 传播,相距10.5 m 的a 、b 两处的质点振动图象如图中a 、b 所示,则 [ D ] A .该波的振幅可能是20 cmB .该波的波长可能是8.4 mC .该波的波速可能是10.5 m/sD .该波由a 传播到b 可能历时7 s18．如图所示是一列横波上A 、B 两质点的振动图象,该波由A 传向B,两质点沿波的传播方向上的距离Δx=4.0m,波长大于3.0m,求这列波的波速． [解析]由振动图象可知,质点振动周期T=0.4s取t=0时刻分析,质点A 经平衡位置向上振动,质点B 处于波谷,设波长为λ则14x n λλ∆=+〔n=0、1、2、3……〕 所以该波波长为416m4141x n n λ∆==++ 因为有λ>3.0m 的条件,所以取n ＝0,1当n ＝0时,116m λ=,波速1140m /s v Tλ==当n ＝1时,13.2m λ=,波速228.0m /s v Tλ==19、如图所示为一列简谐横波在t=0时刻的图象.此时质点P 的运动方向沿y 轴负方向,且当t=0.55s 时质点P 恰好第3次到达y 轴正方向最大位移处.问：〔1〕该简谐横波的波速v 的大小和方向如何？ 〔2〕从t=0至t=1.2s,质点Q 运动的路程L 是多少？〔3〕当t=1.2s 时,质点Q 相对于平衡位置的位移s 的大小是多少？ 〔1〕此波沿x 轴负向传播在t1=0到t2=0.55s 这段时间里,质点P 恰好第3次到达y 正方向最大位移处则有 <2+错误!>T=0.55s 解得 T =0.2sOy /cm5-50.20.4/s0.20.4t /sOy /cm5-5质点 质点y /cmx /m0 0.2 P-Q0.42.5由图象可得简谐波的波长为λ=0.4m则波速 v= 错误! =2m/s〔2〕在t1=0至t3=1.2s这段时间,质点Q恰经过了6个周期,即质点Q回到始点,由于振幅A=5cm 所以质点Q运动的路程为 L=4A×6=4×5×6cm=120cm〔3〕质点Q经过6个周期后恰好回到始点,则相对于平衡位置的位移为s=2.5cm20．图所示为一列简谐波在t1＝0时刻的图象．此时波中质点M的运动方向沿y轴负方向,且t2＝0.55 s时质点M恰好第3次到达y轴正方向最大位移处．试求：<1>此波沿什么方向传播？<2>波速是多大？<3>从t1＝0至t3＝1.2 s,质点N运动的路程和t3时刻相对于平衡位置的位移分别是多少？解析：<1>此波沿x轴负方向传播．<2>在t1＝0到t2＝0.55 s这段时间时,质点M恰好第3次到达沿y轴正方向的最大位移处,则有：<2＋错误!>T＝0.55 s,得T＝0.2 s.由图象得简谐波的波长为λ＝0.4 m,则波速v＝错误!＝2 m/s.<3>在t1＝0至t3＝1.2 s这段时间,波中质点N经过了6个周期,即质点N回到始点,所以走过的路程为s＝6×5×4 cm＝120 cm.相对于平衡位置的位移为2.5 cm.。

高中物理机械波题解析机械波是物理学中的重要概念，涉及到波动的传播和性质。

在高中物理中，机械波的题目常常出现，考察学生对波动方程、波速、频率等概念的理解和应用能力。

本文将通过几个具体的题目来解析机械波的相关知识点，帮助高中学生更好地理解和应对这类题目。

题目一：一根细绳，两端固定在两个固定点之间。

在细绳上有一个固定不动的点源，波源频率为f，波速为v。

当细绳上的波传播到距离固定点源的距离为d处时，波的相位差为π/2。

求细绳上的波长。

解析：根据题目中的描述，我们可以得到如下信息：波源频率为f，波速为v，波的相位差为π/2。

首先，我们需要知道波的相位差与波长之间的关系。

相位差是指两个波峰（或波谷）之间的相位差，而波长是指两个波峰（或波谷）之间的距离。

根据波的相位差与波长之间的关系，我们可以得到：相位差= 2π(Δx/λ)其中，Δx为两个波峰（或波谷）之间的距离，λ为波长。

根据题目中的描述，波的相位差为π/2，代入上述公式，可以得到：π/2 = 2π(d/λ)化简得到：λ = 4d所以，细绳上的波长为4d。

题目二：一根弦上的波动方程为y(x,t) = 0.1sin(4πt - 2πx)，其中x和t的单位分别为m和s。

求波速和频率。

解析：根据波动方程y(x,t) = Asin(2πft - 2πλx)，我们可以得到波速和频率的关系。

波速v表示波动在单位时间内通过的距离，频率f表示单位时间内波动的周期数。

根据波动方程中的参数，我们可以得到：波速v = λf其中，λ为波长，f为频率。

根据题目中的波动方程，我们可以看出波长为2π。

所以，波速v = 2πf。

根据题目中的波动方程，我们可以看出频率为4π。

所以，频率f = 4π。

综上所述，波速为2πf，频率为4π。

通过以上两个例题的解析，我们可以看到，在解决机械波的题目时，我们需要熟练掌握波动方程、波速、频率等概念，并能够根据题目中给出的条件进行计算。

此外，我们还需要理解波的相位差与波长之间的关系，以及波速和频率之间的关系。

高中物理力学中机械波问题的解题技巧机械波是高中物理力学中的重要内容之一，涉及到许多具体的解题技巧。

在本文中，我将为高中学生和他们的父母介绍一些解决机械波问题的方法，并通过具体的题目来说明每个问题的考点和解题思路。

首先，我们来看一道关于波速的题目。

题目如下：一根绳子上的波速为v，频率为f，求波长λ。

这是一道基础的波速公式题目，我们可以通过公式v = fλ来解决。

根据这个公式，我们可以得到波长λ = v / f。

通过这个例子，我们可以看到解决这类题目的关键是熟练掌握波速公式，并能够根据已知条件进行适当的代入计算。

接下来，我们来看一道关于波的叠加的题目。

题目如下：两个频率相同的波沿同一方向传播，相遇后产生了干涉现象。

当两个波的相位差为π/2时，产生了最大干涉效果。

求两个波的波长。

这是一道典型的波的叠加题目，我们可以通过波的叠加原理来解决。

根据叠加原理，当两个波的相位差为π/2时，产生最大干涉效果，即达到最大振幅。

而相位差为π/2对应着波长的一半，即λ/2。

所以，我们可以得到波长λ = 4π。

然后，我们来看一道关于驻波的题目。

题目如下：一根弦两端固定，产生了一个驻波。

当弦上某一点的振幅最大时，该点距离弦的一端的距离为1/4波长。

求弦上任意一点的振幅。

这是一道典型的驻波题目，我们可以通过驻波的特点来解决。

根据驻波的特点，振幅最大的点位于波节和波腹之间的中点，即距离弦的一端的距离为1/4波长。

所以，我们可以得到振幅最大的点距离弦的一端的距离为1/4波长。

而振幅最大的点位于波节和波腹之间的中点，所以振幅最大的点距离波节的距离为1/8波长。

通过这个例子，我们可以看到解决这类题目的关键是熟练掌握驻波的特点，并能够根据已知条件进行适当的代入计算。

最后，我们来看一道关于声音的题目。

题目如下：一位学生站在一个大厅的一端，他听到了另一位学生在大厅的另一端发出的声音。

已知声音的速度为340m/s，大厅的长度为17m，求学生听到声音的时间。

机械波的几种常见问题黄世波机械振动和机械波的问题在近年的高考理综中都有考查，这是高中物理力学板块中相对独立的一部分，根据题目的特点，在处理时有一些独特的方法。

机械波产生的机理可概括为“带动”二字，即波源的振动带动旁边质点的振动，旁边质点带动更远处质点振动，这样依次“带动”，就将波源产生的振动沿介质传播出去，形成机械波。

机械波的特点较多，诸如在波的传播方向上，各质点都重复波源的振动，离波源近的质点先开始振动，离波源远的质点后开始振动；在波的传播方向上，相距波长整数倍的质点振动步调一致，相距半波长奇数倍的质点振动步调相反；波传播的是振动和能量，而不是介质；经历一个周期的时间，波向外传播一个波长的距离；以及波速公式v＝λ/Ｔ等等，这些特点可以用来帮助分析机械波的有关问题。

下面就根据机械波的特点，以简谐横波为例介绍几种常见题型。

一、波的传播方向和质点的振动方向横波，波的传播方向和质点的振动方向是相互垂直的，常见题目已知其中一个方向而让我们判定另一个方向。

可以根据机械波形成的机理来进行分析，这里介绍一种“带动法”，即离波源近的质点先振动，带动离波源远的质点振动。

例1．如图1为一列沿x轴正向传播的简谐横波在某一时刻的波形曲线，试确定图中A、B质点的振动方向。

解析：波沿x轴正向传播，可知波源位于左侧，于是在A点的左侧（靠近波源一侧）附近．．选一点B’，认为A’点带动A点．．选一点A’，在B点的左侧（靠近波源一侧）附近振动，B’点带动B点振动。

如图2，选出A’点、B’点后，发现A’点在的A点上方，故带动A点向上振动；B’点在B点的下方，故带动B点向下振动。

如果已知波形和其中一个质点的振动方向，也可以判定波的传播方向。

如图3已知简谐横波的波形和A点的振动方向，可判定波的传播方向。

由于A点向上振动，故在A点上方附近选一点A’，认为是A’点带动A点振动，A’点离波源较近；选出A’点后，发现它在A点右侧，所以波源在右侧，波向左传播。

机械波的多解成因及解题策略机械振动在介质中传播形成机械波。

在波源附近，机械波以波源为中心向介质中各个方向传播，介质中各质点在各自的平衡位置附近上下振动；在传播过程中，波形图象每隔一定的时间和空间都会重复出现；在传播方向上，介质中两质点间距离与波长的关系不确定。

由于机械波在时间和空间上的周期性。

传播方向的双向性，质点振动方向的不确定性，以及波长、周期的不确定性，是导致波动习题多解的主要原因。

在解题中，如果不能透彻全面的分析题意，容易出现漏解或者用特解代替通解等现象，下面通过几个例子来说明解横波题中应注意的策略：一、介质中质点振动方向的不确定性是造成多解的原因介质中质点既可能向纵轴的正方向运动，也可能向纵轴负方向运动。

所以题中可能出现多解。

例1一列沿X轴传播的波，在t1和t2两时刻的波形图中的实线和虚线所示，设波速，则图中质点P在这段时间内通过的路程可能是（）A．10cm B．20cm C．30cm D．40cm解题策略：P质点可能向上振动，也可能向下振动，在这段时间内，P点可能完成（1/4+n）个全振动，也可能完成（3/4+n）个全振动，所以通过的路程S1＝40（n+1/4）cm，S2＝40（n+3/4）cm，（n＝0，1，2…），当n＝0时，S1＝10cm，S2＝30cm。

A、C选项正确。

二、传播方向的双向性造成波的多解的又一原因在一维空间传播的机械波，如果没有指明传播方向，则波有向两个方向传播的可能。

例2一列横波在X轴上传播，t1＝0和t2＝0．005S的波形如下图所示的实线和虚线，求（1）设周期大于t2－t1，求波速。

（2）设周期小于t2－t1，且，求波的传播方向。

解题策略：因△t＝t2－t1<T，所以波传播的距离可以直接，由图读出，若波向右传播，则在0．005s内传播了2米，则v右＝，若波向左传播，则左0．005内传播了6m，则，v左＝，（2）△t＝t2－t1>T，所以波传播的距离大于一个波长，在0．005S内传播的距离，即，故波向x轴负向传播。