机械波多解问题的成因及对策

机械波的多解成因及解题策略机械振动在介质中传播形成机械波。

在波源附近，机械波以波源为中心向介质中各个方向传播，介质中各质点在各自的平衡位置附近上下振动；在传播过程中，波形图象每隔一定的时间和空间都会重复出现；在传播方向上，介质中两质点间距离与波长的关系不确定。

由于机械波在时间和空间上的周期性。

传播方向的双向性，质点振动方向的不确定性，以及波长、周期的不确定性，是导致波动习题多解的主要原因。

在解题中，如果不能透彻全面的分析题意，容易出现漏解或者用特解代替通解等现象，下面通过几个例子来说明解横波题中应注意的策略：一、介质中质点振动方向的不确定性是造成多解的原因介质中质点既可能向纵轴的正方向运动，也可能向纵轴负方向运动。

所以题中可能出现多解。

例1一列沿X轴传播的波，在t1和t2两时刻的波形图中的实线和虚线所示，设波速，则图中质点P在这段时间内通过的路程可能是（）A．10cm B．20cm C．30cm D．40cm解题策略：P质点可能向上振动，也可能向下振动，在这段时间内，P点可能完成（1/4+n）个全振动，也可能完成（3/4+n）个全振动，所以通过的路程S1＝40（n+1/4）cm，S2＝40（n+3/4）cm，（n＝0，1，2…），当n＝0时，S1＝10cm，S2＝30cm。

A、C选项正确。

二、传播方向的双向性造成波的多解的又一原因在一维空间传播的机械波，如果没有指明传播方向，则波有向两个方向传播的可能。

例2一列横波在X轴上传播，t1＝0和t2＝0．005S的波形如下图所示的实线和虚线，求（1）设周期大于t2－t1，求波速。

（2）设周期小于t2－t1，且，求波的传播方向。

解题策略：因△t＝t2－t1<T，所以波传播的距离可以直接，由图读出，若波向右传播，则在0．005s内传播了2米，则v右＝，若波向左传播，则左0．005内传播了6m，则，v左＝，（2）△t＝t2－t1>T，所以波传播的距离大于一个波长，在0．005S内传播的距离，即，故波向x轴负向传播。

机械波多解问题分类解析及策略研究机械波的多解问题是教学难点，也是高考的热点。

考生往往不能正确判断多解问题的产生原因，从而造成漏解或错解。

本文就2008——2011年高考中出现的机械波多解试题作分类解析，探究机械波多解问题的解题策略。

１、传播方向不确定导致的多解问题波总是由波源出发，并由近及远地向前传播。

波在介质中传播时，介质中的各个质点的振动情况可以根据波的传播方向确定。

反之亦然。

但是，如果题中的已知条件不能确定波的传播方向或者不能确定质点的振动方向，则求解时必须分情况讨论，从而导致了波的多解。

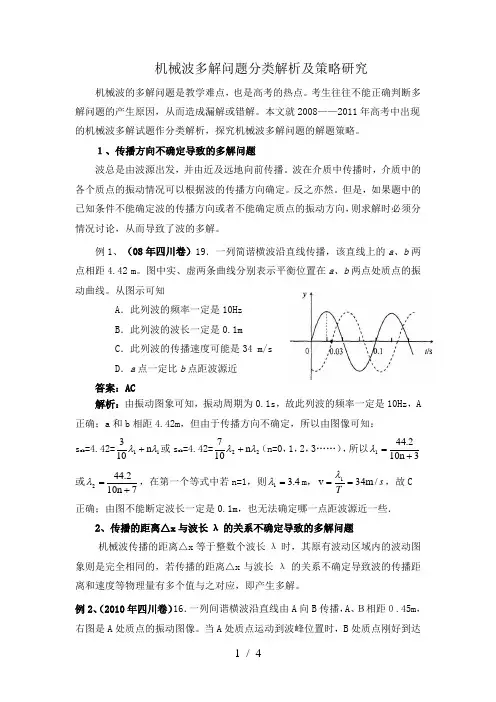
例1、（08年四川卷）19．一列简谐横波沿直线传播，该直线上的a 、b 两点相距4.42 m 。

图中实、虚两条曲线分别表示平衡位置在a 、b 两点处质点的振动曲线。

从图示可知A ．此列波的频率一定是10HzB ．此列波的波长一定是0.1mC ．此列波的传播速度可能是34 m/sD ．a 点一定比b 点距波源近答案：AC解析：由振动图象可知，振动周期为0.1s ，故此列波的频率一定是10Hz ，A 正确；a 和b 相距4.42m ，但由于传播方向不确定，所以由图像可知：s ab =4.42=11n 103λλ+或s ab =4.42=22n 107λλ+（n=0，1，2，3……），所以3n 102.441+=λ或7n 102.442+=λ，在第一个等式中若n=1，则4.31=λm ，s T /m 34v 1==λ，故C 正确；由图不能断定波长一定是0.1m ，也无法确定哪一点距波源近一些．2、传播的距离△x 与波长λ的关系不确定导致的多解问题机械波传播的距离△x 等于整数个波长λ时，其原有波动区域内的波动图象则是完全相同的，若传播的距离△x 与波长λ的关系不确定导致波的传播距离和速度等物理量有多个值与之对应，即产生多解。

例2、（2010年四川卷）16．一列间谐横波沿直线由A 向B 传播，A 、Ｂ相距０.45m ，右图是A 处质点的振动图像。

关于机械波多解问题的例析山东临沂双月园学校（276017）刘忠涛机械波多解问题历来是各级各类考试中经常考察的热点，也是高中物理教学中的一个重点和难点。

学生在求解机械波问题时，往往由于对波动的实质理解不深刻、对题目中隐含条件挖掘不透彻、对已知条件使用不全面等，常常会出现解答不完整而造成漏解。

本文限于横波沿一条直线传播的情形，就常见的机械波多解问题通过剖析其成因进行归类例析，力求帮助学生掌握解决此类问题的根本。

一、波传播的“双向性”带来的多解问题机械波在同种介质中沿一条直线传播的情形下，波的传播方向有两种可能，这就是波传播的“双向性”。

当题目没有明确波的传播方向时，我们必须要考虑波传播的“双向性”，才能得出完整的答案。

例1如图1所示，一列简谐横波以速率v传播，t1时刻的波形为实线，t2时刻的波形为虚线。

已知△t= t2- t1=0.06s，且△t小于一个周期T。

则下列关于该列波传播的周期与速率的判断，可能正确的是( )。

A．T=0.24s，v=50m／sB．T=0.08s，v=150m／sC．T=0.24s，v=150m／sD．T=0.08s，v=50m／s解析：本题没有明确波的传播方向，因此需要考虑波传播的“双向性”。

由图1可知，该波的波长为λ=12m。

（1）若波沿+x方向传播，由图1可看出，波在△t内传播的最小距离为△S=λ／4。

又则波速大小v=△s／△t=λ／T =50m ／s.（2）若波沿－x 方向传播，同理可得另一组解T=0.08s ，v=150m ／s.故本题正确选项为A 、B 。

二、波传播的周期性带来的多解问题机械波在介质中传播的过程中，由于介质质点做周期性的振动，因而波的图像也具有周期性。

这种周期性表现在两个方面：时间上的周期性和空间上的周期性。

（一）波传播的时间上的周期性产生多解设某简谐波周期为T ，传播过程中在时刻t 各振动质点形成一波形，经过时间△t＝nT （n=0，1，2，3，……）各振动质点又回到t 时刻的位置。

高中物理：机械波多解问题机械波的多解问题产生的根本原因是由于机械波图形的周期性重复。

因此我们在求解该类问题时，要重视图像的功能，对图像进行分析，挖掘隐含条件，结合传播方向，利用波动知识解决问题。

1、传播方向导致的多解问题波源起振后产生的波可以在介质中向四周传播。

若题中没有特别注明传播方向，则求解时必须讨论其传播方向，从而导致了波的多解问题。

例1、如图所示，绳中有一列正弦横波，沿x轴传播，，b是绳上两点，它们在x轴上的距离小于一个波长，当点振动到最高点时，b点恰好经过平衡位置向上运动。

试在图上、b之间画出波形图。

分析：本题没有注明波的传播方向，所以需要对波向＋x轴，－x 轴方向传播讨论。

由于、b间距离小于一个波长。

因此、b间不足一个波长，其图像如图乙所示，（1）为波向＋x轴传播时的波形；（2）是波沿－x轴传播时的波形。

2、波长大小导致的多解问题因题中没有给定波长的确切条件，故引起答案的不确定性导致多解问题。

例2、如图甲所示，一根张紧的水平弹性长绳上的、b两点，相距14．0m。

b点在点右方，当一列简谐波沿此绳向右传播时，若点位移达到正向极大时，b点位移恰好为零，且向下运动。

经过1．00s后，点位移为零，且向下运动，而b点的位移恰好达到负向极大，则这列简谐波的波速可能等于：A．4．67m/sB．6m/sC．10m/sＤ．14m/s分析：此题虽然已说明了波的传播方向，但满足题设条件的、b 两点可以有无数个可能位置，图乙中的b1、b2、b3……等。

只可以写出、b间距的通式；（n＝0、1、2……）。

从而波速的答案也是系列解答，经求解可知A、C为正确答案。

3、波形周期导致的多解问题简谐机械波是周期性的，每经过一个周期波形与原波形重复，从而导致了问题的多解性。

例3、一列横波在某时刻的波形图如图中实线所示，经0．02s后波形如图中虚线所示，则该波的波速和频率f可能是（）A．＝5m／sB．＝45m／sC．f＝50HzD．f＝37．5Hz分析：此题波的传播方向不确定，需分向＋x轴和向－x轴传播两种情况讨论。

专题机械波的多解问题一．造成多解的原因以及处理方法1 原因：波的传播方向不确定。

解决方法：分两种情况分别讨论2.原因:时间与周期的关系不确定造成多解。

解决方法：找出时间与周期的对应关系。

常见题型：波形变化题3.原因:一列波上不同的两个振动质点之间的距离与波长的关系不确定造成多解解决方法：画某一时刻(如t=0时刻）的波形图,找出两质点可能的位置，确定距离与波长的对应关系。

常见题型：题目中会给出两个质点的振动情况二．确定时间与周期或者距离与波长的关系时，有两个思路:其一是根据质点振动确定关系；其二是根据波的平移确定关系。

注意：灵活运用对应关系：振动一个周期的时间,波传播一个波长的距离.振动半个周期的时间，波传播半个波长的距离。

振动1/4个周期的时间，波传播1/4个波长的距离.振动几分之几个周期的时间,波传播几分之几个波长的距离。

三．例题：1．如图所示,一列简谐波在x轴上传播,实线和虚线分别表示前后间隔1s的两个时刻的波形图，则这列简谐波的波速可能是A.0.60m/sB. 0。

75m/sC. 1。

05m/s D。

1.15m/s2．如图所示，实线是一列简谐横波某时刻的波形，虚线是经过0。

5s后的波形．已知波的周期为T，而且0。

25s＜T＜0.5s,下列说法中正确的是A。

当波向x轴的正方向传播时，该波的波速为7m/sB。

当波向x轴的正方向传播时，在这0.5s内，x=1。

5m处的质点通过的路程为50cmC. 当波向x轴负方向传播时，x=1。

5m的质点M比x=1。

75m的质点N在0.5s内通过的路程少D. 当t＝0.1s时.x＝1.5m处的质点的位移一定是03．一列沿x轴正方向传播的简谐横波，t=0时刻的波形如图中实线所示,t=0。

2s时刻的波形如图中的虚线所示,则正确的是( ）A。

质点P的运动方向沿y轴正方向B。

波的周期可能为0.27sC。

波的频率可能为8.75HzD。

波的传播速度可能为150m/s4．一列简谐横波沿x轴正方向传播，在x=12m处的质点的振动图线如图1所示，在x=18m处的质点的振动图线如图2所示。

机械波多解问题详解引言机械波是指由振动物体产生的波动现象。

在机械波的传播过程中，经常会遇到多解问题，即存在不止一种解释或解决办法。

本文将深入探讨机械波多解问题，并提供详细解释和示例。

什么是机械波多解问题？机械波多解问题指的是，在机械波传播过程中，存在多种可能的解释或解决办法。

这些解释或解决办法可能会导致不同的波动现象或结果。

机械波多解问题在物理学和工程学中都具有重要的意义。

机械波多解问题的原因机械波多解问题的产生主要是由于以下原因：1. 边界条件的不确定性在机械波传播过程中，边界条件的不确定性可能导致多解问题。

边界条件是指波传播过程中的边界或限制条件，如波的幅度、波速、波长等。

不同的边界条件可能会导致不同的波动效果。

2. 环境中存在多种影响因素机械波的传播环境中常常存在多种影响因素，如介质的性质、外界的扰动等。

这些因素可能会对波动过程产生影响，并导致多种解释或解决办法。

3. 不完全的物理模型在研究机械波的传播过程中，我们通常会使用一定的物理模型来进行分析。

然而，由于模型的简化或忽略了一些细节，可能会导致多种解释或解决办法。

机械波多解问题的应用机械波多解问题的研究对于物理学和工程学领域有着广泛的应用，以下是几个典型的应用领域：1. 声波传播在声学研究中，机械波多解问题的研究能够帮助我们更好地理解声波在不同介质中的传播规律。

通过探究声波的多解问题，可以更好地解释和预测声音的传播情况，这对于声学工程和声学设计有着重要的意义。

2. 地震波传播地震波是一种特殊的机械波，其传播过程中也存在多解问题。

研究地震波的多解问题有助于预测地震的传播路径、强度和震中位置等。

这对于地震预警和地震工程有着重要的应用价值。

3. 光波传播光波是另一种机械波，其在光学领域中的传播过程也存在多解问题。

通过研究光波的多解问题，可以改善光学器件的设计和性能，为光学通信、激光技术等领域的发展提供支持。

机械波多解问题的解决方法对于机械波多解问题的解决，常用的方法包括以下几种：1. 理论推导和模型分析通过理论推导和模型分析，可以对机械波多解问题进行深入研究。

形成机械波的多解问题原因与应试对策作者：胡朝平来源：《中学生理科应试》2021年第11期机械波的多解问题是高中物理的一个难点，也是历来高考中的热点.学生在求解机械波问题时，往往由于对波动的实质理解不深刻、对题目中隐含条件挖掘不透彻、对已知条件使用不全面等，常常会出现解答不完整而造成漏解.本文限于横波沿一条直线传播的情形，就常见的机械波多解问题通过剖析其成因进行归类例析，力求帮助大家掌握解决此类问题的方法.一、造成波动问题多解的原因有传播方向、波长大小、波形周期、质点振动方向、传播时间、质点振动图像.1.传播方向导致的多解问题波源起振后产生的波可以在介质中向四周传播.若题中没有特别注明传播方向，则求解时必须讨论其传播方向，从而导致了波的多解问题.例1 一列简谐横波在t=0时刻的波形如图1中的实线所示，t=0.02 s时刻的波形如图1所示中虚线所示.若该波的周期T大于0.02 s，则该波的传播速度可能是（）.A.1 m/sB.2m/sC.3m/sD.5 m/s图1解析由于该波的周期大于0.02 s，则波沿传播方向传播的距离小于一个波长，即Δx<8 cm.若波向右传播，则Δx=2 cm，v=ΔxΔt=0.020.02 m/s=1 m/s若波向左传播，则Δx=6 cm，v=ΔxΔt=0.060.02 m/s=3 m/s故A、C正确.答案：AC2.波长大小导致的多解问题因题中没有给定波长的确切条件，故引起答案的不确定性导致多解问题.例2 一列简谐横波沿直线传播，某时刻该列波上正好经过平衡位置的两质点相距6 m，且这两质点之间的波峰只有一个，则该简谐波可能的波长为（）.A.4 m、6 m和8 mB.6 m、8 m和12 mC.4 m、6 m和12 mD.4 m、8 m和12 m解析画出符合条件的所有可能波形，如图2所示.分别有λ2 =6 m，λ=6 m，3λ2=6 m，则λ可能为4 m、6 m和12 m，C正确.图2答案：C3.波形周期导致的多解问题简谐机械波是周期性的，每经过一个周期波形与原波形重复，从而导致了问题的多解性.例3 如图3所示中实线是一列简谐波在某一时刻的波形图线，虚线是0.2s后它的波形图线.这列波可能的传播速度是.图3解析从图上可以看出λ=4m，当波沿x正方向传播时，两次波形之间间隔的时间为：14T，114T，214T，…，4n+14T.而4n+14T=0.2sT=4×0.24n+1s由波速公式v=λT代入数据得：v=4n+30.2 m/s=20n+5 m/s （n=0，1，2，…）;当波沿x负方向传播时，两次波形之间间隔的时间为：34T，134T，234T，…，4m+34T4m+34T=0.2，T=4×0.24m+3，由波速公式v=λT代入数据得：v′=4m+30.2 m/s=20m+15 m/s （m=0，1，2，…）此题的答案为：（20n+5） m/s，（n=0，1，2，…）和（20m+15） m/s，（m=0，1，2，…）.答案：（20n+5）m/s，（n=0，1，2，…）和（20m+15） m/s，（m=0，1，2，…）4.质点振动方向导致多解问题例4 一根张紧的水平弹性长绳上的a、b两点，相距14.0 m，b点在a点的右方，如图4所示.当一列简谐横波沿此长绳向右传播时，若a点的位移达到正极大时，b点的位移恰为零，且向下运动，经过1.00 s后，a点的位移为零，且向下运动，而b点的位移达到负极大，则这简谐横波的波速可能等于（）.A.4.67 m/sB.6 m/sC.10 m/sD.14 m/s图4 图5解析由于波向右传播，据“a点位移达正极大时，b点的位移恰为零，且向下运动”，可画出此时a、b间的最简波形，如图5所示.因未明确a、b距离与波长的约束关系，故a、b间的距离存在“周期性”.即n1+34λ=ab=14m （n1=0，1，2，…）因所给定时间与周期的关系未知，故运动时间也存在“周期性”.即（n2+14）T=Δt=1.00 s （n2=0，1，2，…）因此可能的波速为v=λT=14（4n2+1）4n1+3m/s当n2=0，n1=0时，v=4.67 m/s;当n2=0，n1=1時，v=2 m/s;（n2=0，v随n1增大还将减小.）当n2=1，n1=0时，v=23.3 m/s;（n1=0，V随n2的增大而增大.）当n2=1，n1=1时，v=10 m/s;据以上计算数据，不可能出现B和D选项的结果，故选项A、C正确.答案：AC5.传播时间导致的多解问题题目中所给定的时间条件不充分，可能比一个周期长，可能比一个周期短，从而导致了多解问题的出现.例5 某时刻的波形图如图6所示，波沿x轴正方向传播，P点的横坐标x=0.32 m.从此时刻开始计时.图6（1）若P点经0.4 s第一次达到最大正位移，求波速.（2）若P点经0.4 s到达平衡位置，波速又如何？解析（1）依题意，经时间Δt=0.4 s，波向右传播的距离Δx=0.32 m-0.2 m=0.12 m，此时P 点恰好第一次达到最大正位移波速v=ΔxΔt=0.120.4 m/s=0.3 m/s.（2）波向右传播Δx′=0.32 m，P点恰好第一次达到平衡位置，由波的周期性可知，波可能传播的距离Δx′=0.32+λ2n，（n=0、1、2、3…）波速v′=Δx′Δt=0.32+0.82n0.4 m/s=（0.8+n） m/s，（n=0、1、2、3…）答案：（1）0.3 m/s （2）（0.8+n） m/s，（n=0、1、2、3…）6.波动图像上和质点运动导致的多解问题在波动问题中，往往只给出完整波形的一部分，或给出几个特殊点，而其余信息均处于隐含状态.这样波形就有多种情况，形成波动问题的多解性.例6 一列正弦横波在x轴上传播，a、b是x轴上相距sab=6m的两质点，t=0，b点正好振动到最高点而a点恰好经过平衡位置向上运动，已知这列波的频率为25 Hz.（1）设a、b在x轴上的距离小于一个波长，试求出该波的波速.（2）设a、b在x轴上的距离大于一个波长，试求出该波的波速，若波速为40 m/s时，求波的传播方向.图7解析（1）若波向右传播，a和b两质点应于如图7所示的a1和b1的两位置，sab=34λ1=6m，λ1=8m，向右传播的波速v1=λ1f=200 m/s.若波向左传播，a和b两质点应分别位于图7中a2和b1两位置，sab=14λ2=6 m，λ2=24 m，向左传播的波速v2=λ2f=600 m/s.（2）因a，b在x轴上的距离大于一个波长，若波向右传播，a质点若位于图7中a1的位置，则b质点可位于b1，b2，…等位置，此时，sab=34λ右+nλ右=6 m，（n=1，2，3，…），λ右=244n+3 m，向右传播的波速v右=λ右f=6004n+3 m/s，（n=1，2，3，…）若波向左传播，a质点若位于图7中的a2的位置，则b质点可位于b1，b2，…等位置，此时，sab=34λ左+nλ左=6 m，λ左=244n+1 m.向左传播的波速 v左=λ左f=6004n+1 m/s，（n=1，2，3，…）当波速为40 m/s时，该波向左传播，应有：6004n+1 =40，n=144，无整数解，故不可能向左.设波向右传播，有6004n+3=40，n=3，故可以判定当波速为40 m/s时，波传播的方向是由左向右.答案：（1）600 m/s （2）40 m/s例7 一简谐横波沿水平绳沿x轴负方向以v=20 m/s的波速传播.已知t=0时的波形如图8所示，绳上两质点M、N的平衡位置分别是xM=5 m、xN=35 m.从该时刻开始计时，求：（1）质点N第一次回到平衡位置的时间t;（2）平衡位置在x=20m的质点，其振动的位移随时间变化的表达式（用余弦函数表示）;（3）经过多长时间，质点M、N振动的速度相同.图8解析（1）机械波在均匀介质中匀速传播，波沿x轴负方向传播，平衡位置的振动状态距N点t=Δxv=50-3520s，解得t=0.75 s;（2）由题知A=2 m，λ=40 m，T=λv=2 s，ω=2πT=π（rad/s）该质点与原点的距离为20 m=12λ，则该质点的初相位为φ0=12×2π=π，故该质点的振动表达式为y=Acosωt+φ0=2cos（πt+π）（m）或y=-2cosπt（m）;（3）当某质点位于平衡位置时，其两侧与它平衡位置间距相等的质点速度相同，平衡位置的振動状态传播到MN中点的距离Δx′=λ4+nλ2（n=0，1，2…）经过的时间t′=Δx′v，解得t′=（n+0.5）（s），（n=0，1，2…）答案：（1）0.75s;（2） y=-2cosπt（m）;（3）t′=（n+0.5）（s），（n=0，1，2…）二、解决波的多解问题的思路一般采用从特殊到一般的思维方法，即找出一个周期内满足条件的关系Δt或Δx，若此关系为时间，则t=nT+Δt（n=0，1，2，…）;若此关系为距离，则x=nλ+Δx（n=0，1，2…）.三、波的多解问题的一般解题步骤（1）根据初末两时刻的波形图确定传播距离与波长的关系通式.（2）根据题设条件判断是唯一解还是多解.（3）根据波速公式v=ΔxΔt或v=λT=λf求波速.（收稿日期：2021-09-10）。