8.2 含有耦合电感电路的分析

格式：pdf
大小：538.68 KB
文档页数：19

下载文档原格式

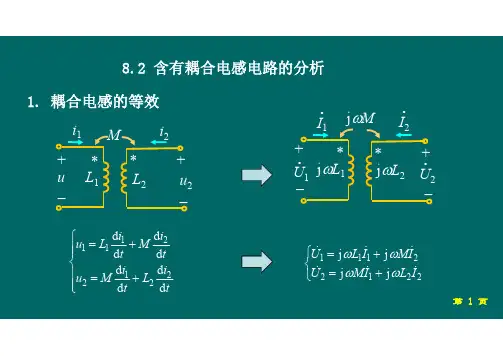
8.2 含有耦合电感电路的分析

第 12 页
例题：
.
I
两个电感线圈按如图所示连接，正弦稳态 +
电压源电压U=50V，角频率=10rad/s，求
R1
开关S在断开和闭合两种状态下各个支路的电流，并求开关S在闭合状态下两个线圈的复功率。
*
jL1 .
.
I2
U jM .
I1
R1 3Ω R2 5Ω L1 0.75H
L2 1.25H M0.6H
8+j32 32.9875.96
_
. I
R1 *
jL1 .
I2=0
jM .
I1 R2 *
jL2
第 14 页
（2）开关S闭合状态下 . I
+
R1
*
jL1 .
.
I2 0
U jM .
I1
R2
*
jL2
_
解法一：互感消去法 . I
+
R1
j(L1+M) .
.
I2
U
.
I1 -jM
R2
_
j(L2+M)
第 15 页
I1
3.47150.30
A
I2
11.09
-
44.85
A
*
U2
jL2 _
_
第 18 页
两个线圈的复功率：
S1 UI* 500 7.7951.50 389.551.50 242.5 + j304.8
S2 U2I1* 0 3.47150.30 0
. I +
R1
*
jL1 .
.
I2
U jM .
i + u1 *– +* u2 –

含耦合电感电路的分析

厶鲁± 鲁ｌ
Ｊｄｔ
堕
ｄｔ
（１）
１．１耦合电感的串联
当两耦合电感异名端相接（即首尾相接）、
且流过同一电流时，称为耦合电感顺串。当两
耦合电感同名端相接（即首首相接或尾尾相
接）、且流过同一电流时，称为耦合电感反串。
可以证明，其去耦等效电感为：
将表达式中的互感系数Ｍ变为．Ｍ即可。
１２６ ·电子技术与软件工程ＥｌｅｃｔｒｏｎｉｃＴｅｃｈｎｏｌｏｇｙ＆ＳｏｆｔｗａｒｅＥｎｇｉｎｅｅｒｉｎｇ
ＥｌｅｃｔｒｏｎｉｃＴｅｃｈｎｏｌｏｇｙ· 电子技术
图３：空芯变压器的相量模型
图７：考虑绕组电阻和铁芯损耗的变压器等效电路
Ｚ２：
图４：空芯变压器去耦等效电路
“１＝＋ｎｕ２Ｊ
ｆ２＝￣－ｎｉ，Ｊ
图（７）中，变压器二次侧电阻损耗和漏
（６）电感已折合到一次侧
式（６）中，当两绕组电压正极性端为同５结语
名端（如图５中所示）时，电压取 “＋”号，
电流取 “．”号；当两绕组电压正极性端为异
式（１）中，Ｍ前取 “＋”号。对正弦交流电路，式（１）可以用相量形式表示，对应的受控源去耦等效电路如图１（ｂ）所示。
（２）两端口电流参考方向从异名端流入。此时，是将电路模型图ｌ（ａ）中Ｌ的同名端标记在下端。同样可得基尔霍夫电压方程如式（１）所示，只是Ｍ前取 “一” 号。对正弦交流电路，其对应的受控源去耦等效电路，只需将图１（ｂ）中受控源的极性反向标记即可。用受控源去耦等效电路求解，虽然比较直观、容易理解，但需列写复杂电路方程，尤其对于不同连接形式的耦合电感，电路方程及解题过程更加麻烦。以下分析几种耦合电感在

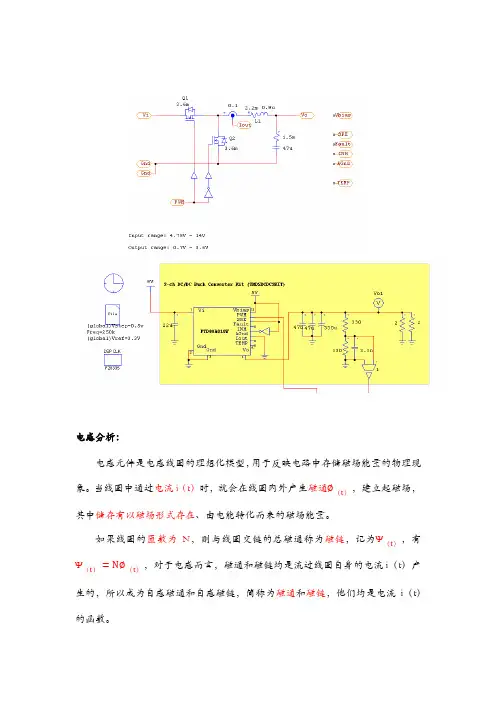
耦合电感的剖析

电感分析：电感元件是电感线圈的理想化模型，用于反映电路中存储磁场能量的物理现象。

当线圈中通过电流i（t）时，就会在线圈内外产生磁通∅（t），建立起磁场，其中储存有以磁场形式存在、由电能转化而来的磁场能量。

如果线圈的匝数为N，则与线圈交链的总磁通称为磁链，记为Ψ（t），有Ψ（t）=N∅（t），对于电感而言，磁通和磁链均是流过线圈自身的电流i（t）产生的，所以成为自感磁通和自感磁链，简称为磁通和磁链，他们均是电流i（t）的函数。

Ψ（t ）=L ∗i （t ）U （t ）=-e （t ）=d ψ（t ）dt=Nd ∅（t ）dt=Ldi （t ）dt其中，U （t ）是电感的端电压，e （t ）是感应电动势。

一般电流和端电压关联，和感应电动势相反。

上面解释了，电感电流的跃变必然伴随着电感储能的跃变。

电感储能与电压无关，和电流有关。

耦合电感：电感仅仅考虑了流过一个线圈本身的时变电流所产生的磁通在自己内部引起的感应电压即自感电压。

但是根据法拉第电磁感应定律，若两个或多个线圈相互邻近，则任一个线圈所载电流变化所产生的磁通，不仅能和自身交链，引起自感电压，而且还会有一部分与邻近的线圈交链，在该线圈上产生互感电压。

耦合电感与电感在开关电源中功能分析：对于电感，感值和匝数恒定，那么伏秒定则的含义是电感磁芯的磁通不变（或者是电流变化不变）。

根据Ψ t =N ∅（t ），Ψ t =L ∗i （t ），电感端电压感应电动势U （t ）=-e （t ）=d ψ（t ）dt=Ldi （t ）dt。

可得UL ∆t =d ψ（t ）∆t Ldt===》d ψ t =∆ψ t =∆N ∅（t ），由于电感匝数恒定，事实上是磁通变化量∆∅（t ）恒定。

而在耦合电感中由于值存在原边、副边、互感，匝数有原边匝数、副边匝数，那么伏安关系变为磁通变化量的恒定。

耦合电感:1拓扑结构的演进文献“非隔离三电平变换器中分压电容均压的一种方法2003.10 中国电机工程学报”中提出了三电平变换器分压电容均压的一种方法，其中三电平BOOST型变换器具有开关管电压应力低，且可获得三电平波形使得滤波元件的大小可大大减小。

电工原理之含有耦合电感电路介绍课件

频率响应分析：通过分析频率响应曲线，可以了解电路的滤波特性、增益、相位等参数，从而优化电路设计。
频率响应的应用：耦合电感电路的频率响应分析在电子技术、通信工程、电力电子等领域具有广泛的应用。
3
耦合电感电路的应用实例
耦合电感电路在滤波器中的应用
01 滤波器类型：低通滤波器、高通滤波器、带通滤波器等
03
耦合电感的大小与线圈的几何形状、相对位 04
耦合电感在电路中起到能量传递、信号处
置、绕线方式等因素有关。
理等作用。
耦合电感的作用
1
耦合电感是电路中两个或多个电感之间的
相互影响
3Байду номын сангаас
耦合电感可以减小电路的噪
声干扰
2
耦合电感可以增强电路的滤
波性能
4
耦合电感可以提高电路的功
率传输效率
耦合电感的分类
电工原理之含有耦合电感电路介绍课件
目录
01. 耦合电感电路的基本概念 02. 耦合电感电路的分析方法 03. 耦合电感电路的应用实例
1
耦合电感电路的基本概念
耦合电感的定义
01
耦合电感是两个或多个电感线圈之间通过
02
耦合电感是电路中一种重要的元件，常用于
磁场相互影响的现象。
滤波、调谐、阻抗匹配等电路中。
自感耦合：两个电感线圈之间通过磁场相互耦合
变压器耦合：两个电感线圈之间通过变压器相互耦合
互感耦合：两个电感线圈之间通过电流相互耦合
电容耦合：两个电感线圈之间通过电容相互耦合
2
耦合电感电路的分析方法
电路分析的基本方法
电路图分析：了
1 解电路的结构和功能

含有耦合电路分析经典篇

含有耦合电路分析经典篇
• 耦合电路的基本概念 • 耦合电路的分析方法 • 耦合电路的经典案例 • 耦合电路的优化设计 • 耦合电路的未来发展
01
耦合电路的基本概念
耦合电路的定义
01
耦合电路是指由两个或多个电路之间存在相互作用的电路，这种相互作用是通过元件之间的耦合实现的。
02
耦合电路中的元件可以是电阻、电容、电感等，这些元件之间通过耦合关系相互影响，从而形成一个整体的系统。
频率响应分析方法
通过频率域分析方法，将时域的耦合电路转换为频域表示，进行频谱分析和滤波器设计。
3
频率响应的应用
用于分析信号在耦合电路中的传输特性，以及设计具有特定频率响应的滤波器和振荡器等电子器件。
03
耦合电路的经典案例
变压器耦合电路
变压器耦合电路是一种常见的耦合电路，通过变压器实现信号的
电感器耦合电路的特点是能够实现信号的无损耗传递，同时具有滤波作用，能够抑制高频
噪声干扰。
电容器耦合电路
01
电容器耦合电路是一种利用电容器实现信号传递的耦合电路。
02
电容器耦合电路常用于高频信号传输，如无线通信、雷达等。
03
电容器耦合电路的特点是能够实现信号的隔直流传递，同时具有选频作用，能够选择特定频率的信号进行传输。
等效电路的构建
将耦合电感用等效的电感和电阻替代，形成一个等效的RC或RL 电路。
等效电路的应用
用于简化电路分析，将复杂的耦合电路转换为简单的单端口网络，便于计算和性能分析。
等效电路的局限性
等效电路的精度受限于耦合系数的计算精度和电路近似程度。
耦合电路的频率响应分析
1 2

含有耦合电路要点

第10章含有耦合电感的电路（小结）1、耦合电感的概念理解耦合电感是线性电路中一种重要的多端元件。

分析含有耦合电感元件的电路问题，重点是掌握这类多端元件的特性，即耦合电感的电压不仅与本电感的电流有关，还与其它耦合电感的电流有关，这种情况类似于含有电流控制电压源的电路。

2、含有耦合电感电路的分析分析含有耦合电感的电路一般采用的方法有列方程分析和应用等效电路分析两类。

考虑到耦合电感的特性，在分析中要注意以下特殊性：（1）耦合电感上的电压、电流关系式的形式与其同名端位置有关，与其上电压、电流参考方向有关。

认识到这一点是正确列写方程及正确进行去耦等效的关键。

（2）由于耦合电感上的电压是自感电压和互感电压之和，因此列方程分析这类电路时，如不采用去耦等效，则多采用网孔法回路法，不宜直接应用结点电压法。

（3）应用戴维宁定理（或诺顿定理）分析时，等效内阻抗应按含受探源电路的内阻抗求解法。

但当负载与有源两端网络内部有耦合电感存在时，戴维宁定理（或诺顿定理）不便使用。

3、理想变压器的三个理想化条件理想变压器是在耦合电感元件基础上加进3个理想化条件而抽象出的一类多端元件。

这3个理想化条件是：（1）全耦合，即耦合系数k=1；（2）参数无穷大，即L1，L2，M →∞，但满足L1/L2=常数；（3）无损耗。

4、理想变压器的主要性能在满足上述三个理想化条件下，具有如下性能：（1）变电压。

即元件的初、次级电压满足代数关系22211nu u N N u ±=±=（n 为初次级线圈匝数比）。

（2）变电流。

即元件的初、次级电流满足代数关系211i n i ±=。

（3）变阻抗。

即由理想变压器初级端看进去的输入阻抗为L in Z n Z 2=。

（4）理想变压器在任何时刻吸收的功率为零，是不储能、不耗能、只起能量传输作用的无记忆元件。

5、理想变压器在应用上述性能时需注意以下事项：（1）理想变压器的变压关系式u 1、u 2的参考极性及同名端位置有关。

【电路第五版邱关源】第八章含有耦合电感的电路和谐振电路

对互感电压，因产生该电压的电流在另一线圈上，因此，要确定其符号，就必须知道两个线圈的绕向。这在电路分析中显得很不方便。
引入同名端可以解决这个问题。
同名端：当两个电流分别从两个线圈的对应端子流入，
其所产生的磁场相互加强时，则这两个对应端子称为同名端。同名端用“*”或“”表示。
同名端表明了线圈的相互绕法关系。

U 1 R1 jL1 I jM I
“-”反接

Z1

ZM

I
R
1
I
j L1 M
Z 1 R 1 j L 1 线圈1阻抗

U1
R2
Z M j M 互感阻抗

U

U 2 R2 j L2 I j M I

U2 j L2 M
22
21

L2
di2 dt

M
d i1 dt
二、互感线圈的同名端具有互感的线圈两端的电压包含自感电压和互感电压。表达式的符号与参考方向和线圈绕向有关。
对自感电压，当u, i 取关联参考方向，i与符合右螺旋定则，
其表达式为
u11

d Ψ11 dt

N1
d Φ11 dt

L1
di1 dt
上式说明，对于自感电压由于电压电流为同一线圈上的，只要参考方向确定了，其数学描述便可容易地写出，可不用考虑线圈绕向。对线性电感，用u,i描述其特性，当 u,i取关联方向时，符号为正；当u,i为非关联方向时，符号为负。
2'
同名端的实验测定： R S1i *
1'
*2

含有耦合电感的电路分析

参数表示
耦合电感的参数包括自感、互感、耦合系数等，这些参数用于描述耦合电感的电气特性。
02
耦合电感的等效电路
耦合电感的串联等效电路
总结词
在串联等效电路中，耦合电感被视为一个整体，其等效阻抗由两个电感线圈的互感和总自感共同决定。
详细描述
在串联等效电路中，耦合电感器被视为一个整体，其等效阻抗由两个电感线圈之间的互感和总自感共同决定。互感是指一个线圈的磁场对另一个线圈产生感应电动势的能力，总自感则是每个线圈单独存在时的自感之和。
戴维南定理是电路分析的重要定理之一，适用于含有耦合电感的电路。通过将复杂电路等效为简单电路，简化分析过程。
详细描述
在含有耦合电感的电路中，将电路划分为待求支路和入端电阻网络。然后通过设定入端电阻网络的参考方向，利用戴维南定理求出等效电源电动势和内阻，从而得到待求支路的电压和电流。
04
耦合电感在电路中的应用
成持续的振荡波形。
设计要素
02
振荡器的设计需要考虑反馈系数、放大倍数、选频网络等要素。
耦合电感在振荡器中的作用
03
耦合电感作为选频网络的一部分，决定了振荡器的振荡频率和
稳定性。
THANKS
05
含有耦合电感的电路实例分析
变压器的工作原理分析
变压器原理
变压器是利用耦合电感原理，通过磁场传递能量，实现电压、电流和阻抗的变换。
工作过程
当交流电源施加在变压器的一次绕组时，产生交变磁场，在二次绕组中产生感应电动势，从而实现了电压的变换。
变压比
变压器一次绕组与二次绕组的匝数比决定了输出电压与输入电压的比值。
耦合电感在电路中的作用
1 2
3
实现电能转换

电路分析电子教案耦合电感电路

耦合电感的串联与并联分析
串联分析
当两个耦合电感串联时，其等效阻抗等于两个耦合电感的阻抗之和。
并联分析
当两个耦合电感并联时，其等效阻抗等于两个耦合电感的倒数之和的倒数。
耦合电感的电压电流关系
电压电流关系
在耦合电感电路中，电压和电流之间存在一定的相位差，相位差的大小取决于耦合电感的类型和参数。
在逆变器中，耦合电感电路的应用可以实现直流电向交流电的转换，为家用电器和工业设备提供稳定的电源。
THANKS
感谢观看
02
耦合电感电路的分析方法
耦合电感的等效变换法
等效变换法
通过等效变换，将耦合电感电路转换为简单的电阻电路，从而简化分析过程。
互感系数的等效变换
电压电流的等效变换
通过等效变换，将原电路中的电压电流关系转换为新的电压电流关系，便于分析计算。
将原电路中的互感系数等效变换为新的电阻值，实现电路的等效变换。
具有重要作用。
通过合理设计变压器绕组匝数和排列方式，可以实现对电压和电流的变换，提高电力传输的
效率和稳定性。
耦合电感电路的应用，使得变压器能够实现磁通量在两个或多个绕组之间的传递，从而实现了电压和电流的变换。Leabharlann 无线通信系统中的耦合电感应用
在无线通信系统中，耦合电感电路被广泛应用于天线和信号处理中。
频域分析方法包括频率响应函数法、网络函数法等，这些方法
03
可以通过解析或数值方法求解电路的频率响应。
04
耦合电感电路的稳定性分析
耦合电感电路的稳定性定义
稳定性定义
耦合电感电路在正常工作条件下，能够保持其性能参数（如电压、电流、阻抗等）稳定不变的能力。

《含耦合电感的电路》课件

耦合电感是两个或多个电感器件之间相互耦合的一种电路形式。本节将介绍耦合电感的定义以及耦合系数的概念。
耦合电路的研究
耦合电路具有多种基本形式和特点，需要采用相应的分析方法进行研究。本节将介绍耦合电路的基本形式、特点以及分析器等电子设备中有广泛的应用。本节将介绍耦合电路在这些设备中的具体应用。
实验
通过设计实验，可以更好地理解和应用耦合电路的知识。本节将介绍耦合电路的实验设计、实验结果的分析，以及可能遇到的问题和解决方法。
总结
含耦合电感的电路不仅在电子工程领域中具有重要性，还有着广阔的应用前景。本节将对其重要性、应用前景以及未来发展趋势进行总结。
《含耦合电感的电路》 PPT课件
这个PPT课件介绍了含耦合电感的电路的基本知识和应用。通过学习这个课件，您将了解电感的定义、耦合电感的特点以及耦合电路在放大器、振荡器和滤波器中的应用。
电感简介
电感是电路中重要的元件之一，它可以存储和释放磁场能量。本节将介绍电感的定义和常见的分类。
耦合电感简介

8-含有耦合电感的电路

(L2M)dd2itMddti
i = i1 +i2
i -M
画等效电路：
+
i1
i2
u (L1L2 M2) di L1L2 2Mdt
u –
L1+M
L2+M
三.去耦等效法（消耦法）
M 同正异负
3
M
3
使用条
件：三
L1
L2
L1M
L2M 端联接
同减异加
的两个
1
2
12
耦合电
M
感必须
3
3
有一侧
R1 M
R2
* L1 * L2
②施感电流i1、i2的流入端与另一线圈的端口电压u2、u1
的正极性端是同名端时互感电压u12、u21取正，否则取
负。
2.相量形式：在正弦交流电路中，其相量形式的方程为：
•
•
•
U1 jL1I1jMI2
•
•
•
U2 jL2I2jMI1
应用举例
例：8-1 写出图中各电路的电压、电流关系式。
i1 M i2
+• u_1 L1
第8章含有耦合电感的电路
本章内容
8.1
互感
8.2 含有耦合电感电路的计算
8.3
空心变压器
8.4
理想变压器
佳木斯大学信息电子技术学院
本章学习目的及要求
耦合电感在工程中有着广泛的应用。本章主要介绍了磁耦合现象、互感和互感电压、有互感电路的计算、空心变压器和理想变压器的电压电流关系。重点： 1.互感和互感电压的概念及同名端的含义； 2.含有互感电路的计算； 3.含有空心变压器和理想变压器的电路的

第8章含耦合电感的电路

对应端子称为该两互感线圈的同名端。
? 11
?s
?0
i1 *? N1 i2 ?△ N2 i3
N3 *△
+ u11 – + u21 – + u31 –
u21
?
M21
di1 dt
u31
?
? M31
di1 dt
注线圈的同名端是对于两个互感线圈中的一对端子而言的，
意因此必须每两个线圈分别成对确定。
11
5.4 确定同名端的两类方法
即有
? 1 ? ? 11 ? L1i1
称L1为自感系数，单位亨(H)。
（2）两个线圈的情况
当两个线圈都有电流时，每一线圈的磁链为自磁链与互
磁链的代数和：
? 1 ? ? 11 ? ? 12 ? L1i1 ? M12i2
? 2 ? ? 22 ? ? 21 ? L2i2 ? M21i1
称M12、M21为互感系数，单位亨(H)。
5.2 互感电压的确定必须了解线圈绕向
对互感电压，因产生该电压的的电流在另一线圈上，因此，
要确定其符号，就必须知道两个线圈的绕向。这在电路分析中显
10
得很不方便。为解决这个问题引入同名端的概念。
5.3同名端
当两个电流分别从两个线圈的对应端子同时流入或流出，若所
产生的磁通方向相同而“相助”，即磁通相互加强时，则这两个
?
?
?
U 1 ? j? L1 I1? j? M I 2
?
?
?
U 2 ? ? j? M I1 ? j? L2 I 2
在以上式子中，两线圈的自感磁链和互感磁链“相助”，
注
则互感电压取正，否则取负。这表明，自感磁链和互感磁

第10章含有耦合电感的电路分析

例i
1*

*2
* 1

2
3
1'
2' 1'
2'*

3'
(2)当随时间增大的时变电流从一线圈的一端流入时，将会引起另一线圈相应同名端的电位升高。
同名端的实验确定
+
R S 1i i *
1'
2 *

+
V
2'
–
如图电路，当闭合开关 S 时，i 增加，
di dt
0,
u22'

M
di dt
0
电压表正偏。
+ u11 – + u21 – – u31 +
意义：若电流i1由N1的“ • ”端流入，则在N2中产生的互感电压u21的正极在N2的“• ”端。
11 L1
L2
i1 +
N1 u11
– i2 +
N2 u21
–
21
电路模型
i1
M
+
*
u1 _
L1
i2
*
+
L2
_u2
确定同名端的方法
(1)当两个线圈中电流同时由同名端流入(或流出)时，两个电流产生的磁场相互增强。

L2
di2 dt
写出图示电路电压、电流关系式
2) 用CCVS表示的耦合电感电路
ห้องสมุดไป่ตู้
i1
M
+
*
u1 _
L1
i2
*
+
L2
_u2

电路分析课件-含有耦合电感的电路

u1 L1
i1(t )
di1 dt 1 L1
M
0
t
0 u1(
di2 dt
)d
M L1
i2 (t )
i1 nM:1 i2
+* u_1 L1
*+ L2 _u2
理想變壓器模型
考慮到理想化條件：k 1 M L1L2 L1 , L1 L2 N1 N2 n
M L2 1 L1 L1 n
i1 1
生的互感電壓：
•
•
U oc
jM U S
Z11
•
jMY11U S
一次側對二次側的反映阻抗：
Zeq (M )2Y11
從而可得從負載端看出去的戴維寧等效電路。
例10-21 L1=L2=0.1mH , M=0.02mH , R1=10 , C1=C2=0.01F ,
C1
j M
C2
106rad/s, U s 100o V
+* u_1 L1
_
L2 u2 *+
寫出圖示電路電壓、電流關係式
例已知 R1 10, L1 5H, L2 2H, M 1H,求u(t)和u2(t)
M
+ R1 *
u _
i1 L1
* R2 +
L2
u2
_
i1/A
10
0 1 2 t/s
解
u2 (t )
M
di1 dt
101V0V 0
含有耦合電感的電路
重點 1.互感 2.含有耦合電感電路的計算 3.變壓器原理 4.理想變壓器
10.1 互感
在實際電路中，如收音機、電視機中的中周線圈、振盪線圈，整流電源裏使用的變壓器等都是耦合電感元件。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Leq L1 + L2 2M L1 + L2 2 L1L2 ( L1 L2 )2
4M 顺接
Leq=
0 逆接
第7页
（3）T型联接耦合电感的等效
1）同侧联接
I
jM
I 2
1
**
2
jL1
jL2
I 1
1
j(L1-M)
I
33
I2 I3 - I1
3
U 13
jL I + 11
jMI 2
jω(L1 - M )I1 +
M
耦合系数 k
1
LL 12
M L1L2
互感不可能大于两个自感乘积的均方根值。
第5页
利用耦合电感的顺（正）、逆（反）联接可以测量耦合电感的大小顺接一次，反接一次，就可以测出互感：
L L + L + 2M 顺12
L 逆
L1
+
L2
-
2M
L -L M 顺逆
4
第6页
全耦合时 M L L 12
当 L1 = L2时 , M= L1 = L2
I 2
j(L2+M)
第 10 页
jM
**
jL1 jL2
jM
**
jL1 jL2
jM
**
jL1 jL2
j(L1-M) j(L2-M)
jM
第 11 页
2. 含有耦合电感电路的分析第一种方法： (1) 消去耦合电感(耦合电感等效)； (2) 在正弦稳态下采用相量分析法。
第二种方法： (1) 正弦稳态下采用相量分析法，直接建立含有耦合电感的电路方程。 (2) 注意耦合电感的电压除自感电压外，还应包含互感电压。
8+j32 32.9875.96
_
. I
R1 *
jL1 .
I2=0
jM .
I1 R2 *
jL2
第 14 页
（2）开关S闭合状态下 . I
+
R1
*
jL1 .
.
I2 0
U jM .
I1
R2
*
jL2
_
解法一：互感消去法 . I
+
R1
j(L1+M) .
.
I2
U
.
I1 -jM
R2
_
j(L2+M)
第 15 页
_
I U 500 7.79 - 51.50 A Z 6.4251.50
R1
j(L1+M) .
I2 .
I1 -jM
R2
j(L2+M)
第 16 页
分流公式
I1
- jM
R2 +j L2 + M
-
jM
I
- j10 0.6
7.79 - 51.50
5+j10 1.25 + 0.6 - j10 0.6
I1 +
R2 .
*
U2
jL2
_
_
第 19 页
.
I 总阻抗：
Z R1+jL1 + M +R2+jL2 + M / /-jM
+
R1+j
L1
+
M
+
R2+jL2 + M-jM
R2+jL2 + M - jM
. U
5+j101.25 + 0.6 -j10 0.6
3+j100.75+0.6 + 5+j101.25+0.6 - j100.6
6.4251.50Ω
3.47150.30 A
分流公式
I2
R2 +j L2 + M R2 +j L2 + M - jM
I
5+j10 1.25 + 0.6
7.79 - 51.50
5+j10 1.25 + 0.6 - j10 0.6
11.09 - 44.85 A
. I +
. U
_
R1
j(L1+M) .
I2 .
jMI3
U jL I + jMI
23
22
1
jω(L2 - M )I2 + jMI3
I I - I
1
3
2
I 2 2
j(L2-M)
jM
I3
第8页
2）异侧联接
I 1
1
jL1
jM I 2
*
2
jL2
*
I 3
3
I 1
1
j(L1+M)
I 2 2
j(L2+M)
I2 I3 - I1
-jM
3 I3
U jL I - jMI
I1 -jM
R2
j(L2+M)
第 17 页
.
I 解法二：直接利用互感元件伏安方程 +
R1I+jL1I + jMI1 U
R1
R2I1+jL2I1 + jMI U2 0
.
I I1 + I2
U
联立求解上述方程组得支路电流：
*
jM
jL1 .
I2
. I1 +
R2 .
I 7.79 - 51.50 A
第1页
（1）用受控源等效电路替代耦合电感的作用
U1 jL1I1 + jMI2 U2 jMI1 + jL2I2
. I1
+
.
jL1
U1
.+
jM I2 _
_
. I2
+
jL2
.
+
. U2
_ jM I1
_
第2页
(2)串联联接耦合电感的等效
1）顺接(正接)
L1 M L2
i
+ * u1 –
* +
u2
–
+
u
13
11
2
jω(L1+M )I1 - jMI3
U jL I - jMI
23
22
1
jω(L2 +M )I2 - jMI3
I I - I
1
3
2
第9页
举例
i
M
+
i1 * * i2
u
L1
L2
–
i
M
+
i1 *
i2
u
L1
L2
–
*
I
jM
I1
I 2
j(L1－M)
j(L2－M)
I
-jM j(L1+M)
I 1
R2 S
*
jL2
_
第 13 页
解： U 500 V
+ （1）开关S断开状态下
U R1 + R2 I+j L1 + L2 + 2M I
I
U
R1 + R2 +j L1 + L2 + 2M
. 等效电感 U
500
8+j10 0.75 +1.25 + 2 0.6
500
500
1.52 - 75.96 A
i + u1 *– +* u2 –
i
+
u
–
+
去耦等效电路 Leq
u–
u
L1
di dt
-
M
di dt
+
L2
di dt
-
M
di dt
(L1
+
L2
-
2M
)
di dt
=Leq
di dt
u1
u2
第4页
根据逆接(反接)时的等效电感
L L + L - 2M 0 eq 1 2
M
1 2
(
L1
+
L2 )
即互感不可能大于两个自感的算术平均值。
8.2 含有耦合电感电路的分析
1. 耦合电感的等效
i1 M
i2
+* * +
u L1 _
L2
u2 _
.
.
I1 jM I2
+ .
*
U_1 jL1
*
+.
jL2 U2
_
u1
L1
di1 dt
+
M
di2 dt
u2
M
di1 dt
+
L2
di2 dt
U1 jL1I1 + jMI2 U2 jMI1 + jL2I2
第 12 页
例题：
.
I
两个电感线圈按如图所示连接，正弦稳态 +
电压源电压U=50V，角频率=10rad/s，求
R1
开关S在断开和闭合两种状态下各个支路的电流，并求开关S在闭合状态下两个线圈的复功率。
*
jL1 .
.
I2
U jM .
I1
R1 3Ω R2 5Ω L1 0.75H
L2 1.25H M0.6H
–
Leq L1 + L2 + 2M 去耦等效电路
Leq i
+u –
u L di + M di + L di + M di 1 dt dt 2 dt dt

8.2 含有耦合电感电路的分析

合集下载