当前位置：文档之家 › 含有耦合电感的电路(学生用)

含有耦合电感的电路(学生用)

  • 格式：doc
  • 大小：678.01 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

10章 含有耦合电感的电路

10章 含有耦合电感的电路

jω L2 (支路 支路3)L ± 同侧取 同侧取“ 支路 3=±M(同侧取“＋”,异 异
R2
侧取“ 侧取“－”) (支路 1’=L1 m M，M前所取符 支路1)L 支路 ， 前所取符 号与L 号与 3中的相反 (支路 2’=L2 m M，M前所取 支路2)L 支路 ， 前所取 符号与L 符号与 3中的相反
反相串联无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
Z = Z1 + Z 2 = R1 + R2 + jω ( L1 + L2 − 2 M )
R1
L1 u1
2、顺向串联 、 每一耦合电感支路的阻抗为： 每一耦合电感支路的阻抗为：
Z1 = R1 + jω ( L1 + M )
两个耦合线圈的磁通链可表示为： 两个耦合线圈的磁通链可表示为：
ψ 1 = ψ 11 ± ψ 12
= L1i1±Mi2
ψ 2 = ±ψ 21 + ψ 22
= ±Mi1+L2i2 上式表明， 上式表明 ， 耦合线圈中的磁通链与施感电流 线性关系 关系， 成 线性 关系 ， 是各施感电流独立产生的磁通链叠 加的结果。 加的结果。
di di u2 = R2i + ( L2 −M ) dt dt di = R2i + ( L2 − M ) dt
无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
di u = u1 + u 2 = ( R1 + R2 )i + ( L1 + L2 − 2 M ) dt
L1 N1 L2 N2

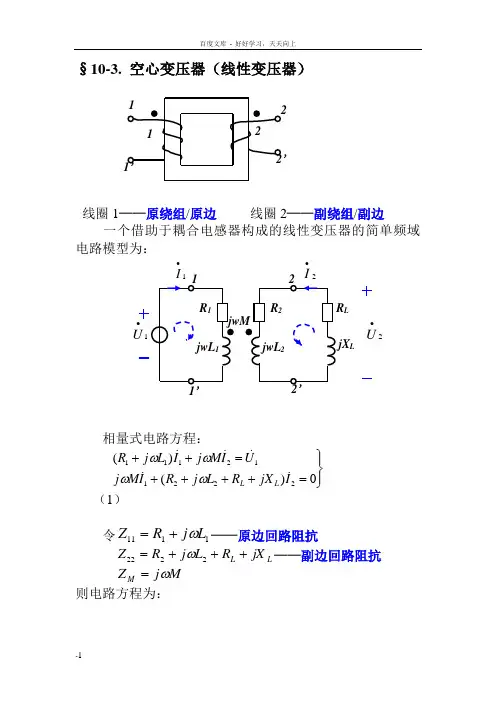
含有耦合电感电路(学生用)2

含有耦合电感电路(学生用)2

§10-3. 空心变压器（线性变压器）线圈1──原绕组/原边 线圈2──副绕组/副边一个借助于耦合电感器构成的线性变压器的简单频域电路模型为：相量式电路方程：⎪⎭⎪⎬⎫=++++=++0)()(222112111I jX R L j R I M j U I M j I L j R L L ωωωω （1）令1111L j R Z ω+=──原边回路阻抗L L jX R L j R Z +++=2222ω──副边回路阻抗 M j Z M ω= 则电路方程为：’LjX L1•U 2•U 1•I 2•I⎪⎭⎪⎬⎫=+=+022*******I Z I Z U I Z I Z M M（2）解方程（2）得2221112221111)(Z M Z U Z Z Z U I M ω+=-+=••（3）11222111112221112)(Z M Z U Z M j Z Z Z U Z Z I M M ωω+-=--=••（4）由（3）得原边等效电路：()222Z M ω──引入阻抗/反射阻抗（reflected impedance ）即副边的回路阻抗通过互感反映到原边的等效阻抗。

注意：反射阻抗的性质与Z22相反； 由（4）得变压器副边的等效电路：1•U 1Z 11()222Z M ω2Z eq111•U Z M j ω•L11222)(Z M L j R Z eq ωω++=例1. 一线性变压器副边接有负载，原边由电压源tv u s sin 210=激励。

变压器参数为Ω=11R ，H M L L 121===，电路如图所示，试就 （1）负载短接（2）负载为C=1F 的电容器分别计算电流1i 与2i解：（1）负载短接u S•MR 1•L 1 S U •1 R 1 22)(L j M ωω •22)(L j R M L j ωωω++︒∠=++︒∠=++=•01011010)(222111j j L j M L j R U I sωωω A1122112)(L j R M L j U L j R M j I sωωωωω+++-=•︒∠=︒∠-=++︒∠⋅+-=180100101101012jj j j∴ A t i sin 2101=A t i )180sin(2102︒+= （2）负载为电容C=1FCj L j M L j R U I sωωωω1)(22111+++=•S U •R 1•2 1122)(1L j R M C j L j ωωωω+++2•IA jj j 01110102=+++︒∠=1122112)(1L J R M C j L j U L j R M j I s ωωωωωω++++-=•A j jj j j j ︒∠-=︒∠-=+++︒∠⨯+-=901001011101012∴ A i 01=A t i )90sin(2102︒+-=例2. 含有线性变压器的电路如图所示L L L jX R Z +=可以自由改变，其余参数有定值，当Ω-=5.15.2j Z L 时，有P Lmax = 5W 。

电路第十章含有耦合电感的电路

电路第十章含有耦合电感的电路
则，自感磁通和互感磁通方感向磁通方向相反，故1，3端
.. . . .. .. . . .. 一致，故1，4是同名端，（不2是，同名端，1，4是同名端，
3也是同名i1 端） i2 （2，3也是同名端i1 ） i2
1 23 4
1 23 4
同名端只与线圈的绕向有关，与电流方向无关。 只要知道线圈的绕向，就能标出同名端。
L L1L2 M2 L1 L2 2M
M2 L1L2
M L1L2 M L1 L2
2
几何平均值（小） 算术平均值（大）
除非两电感相同，一般：几何平均值< 算术平均值
∴用几何平均值求M更严格
∴互感M必须满足 M L1L2 的要求 ∴ M的最大值 Mmax L1L2
3.耦合系数 k M M max
最大值
i(t)
••
u ( t ) L1 L2
i(t)
u(t)
L1 -
di
M
dt +
L2
+
M
di
- dt
utL1d d ti Md d ti L2d d ti Md dti
L1
L2
2Mdi
dt
L
di dt
反接时，串联电感值为
LL1L22M
电感贮能 WL 12LiL2 0
即L一定为正值
L1L22M
M L1 L2 2
实际值
M L1 L 2
0k1
k 反应了磁通相耦合的程度
k=1 k→1 k<0.5 k=0
全耦合
线圈中电流产生的磁通全部与另一个线 圈交链达到使M无法再增加
紧耦合，强耦合
松耦合，弱耦合
无耦合
4.耦合电感的T型等效

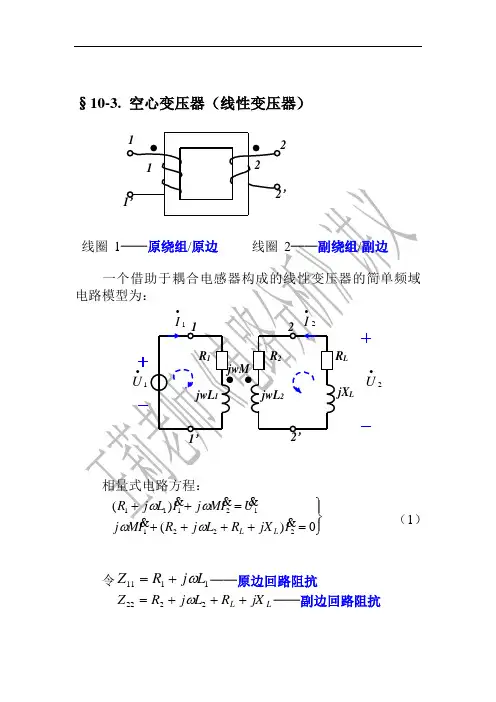
含有耦合电感的电路学生用2

含有耦合电感的电路学生用2

§10-3. 空心变压器（线性变压器）⎭2221L L令1111L j R Z ω+=──原边回路阻抗L L jX R L j R Z +++=2222ω──副边回路阻抗M j Z M ω= 则电路方程为：⎪⎭⎪⎬⎫=+=+022*******I Z I Z U I Z I Z M M （2）解方程（2）得22Z ──引入阻抗/反射阻抗（reflected impedance ）即副边的回路阻抗通过互感反映到原边的等效阻抗。

注意：反射阻抗的性质与Z22相反； 由（4）得变压器副边的等效电路：2Z eq 11∙U Z M j ω∙LL jX222)(MLjRZeqωω++=L1SU∙22)(LjMωω︒∠=++︒∠=++=∙01011010)(222111j j L j M L j R U I sωωω A2112)(M U L j R M j I sωωω+-=∙Cj L j L j R ωωω1211+++ S U ∙112)(L j R M ωω++A jj j 01110102=+++︒∠=2112U L j R M j I s ωω+-=∙采用戴维南定理与最大功率传输定理。

解法1： 副边的去耦合等效电路其开路电压2M 最大功率（传输）为505.015.24142222max ==+⨯==S s M ocL U jU jX R U P∴ VU s 10=耦合系数Z L111S L M U jX R jX ∙+222ML X jX R ++2221121=⨯==L L M X X X k解法2：直接用受控源解 （1）移去L Z 后的电路如图示：等效阻抗 1122L L out jX R +j X j R M +++=1)(222)22(2222MMX j X R -++=R 1R 2当电路实现最大功率传输时5.15.2j Z Z L out +== 由实部、虚部分别相等，得⎪⎪⎪⎨⎧+=-=+5.125.22222M M X X R原边匝数N 1副边匝数N 2电路模型：1将(3)代入（2）得：221212∙∙∙∙+-=I L j L j I M j U M j U ωωωω 1 2i i22122112∙∙∙∙+-=I L j L I M j L U M U ωω由于理想变压器是全耦合变压器,耦合因数k=1，即21L L M =铁芯变压器是近似的理想变压器，广泛用于电力和电子工业中。

10第十章 含有耦合电感的电路

10第十章 含有耦合电感的电路

上 页
下 页
例1-1
i1
M
i2 * + L2 u2 _
i1
M
i2
+ * u1 L1 _
+ * u1 L1 _
L2 *
+ u2 _
试写出图示电路电压、电流关系式
解：
di1 di2 u1 L1 M dt dt
di1 di2 u2 M L2 dt dt
di1 di2 u1 L1 M dt dt di1 di2 u2 M L2 dt dt
R R1 R2
L L1 L2 2M
注意 L L1 L2 2M 0
M 1 ( L1 L2 ) 2
返 回 上 页 下 页
互感的测量方法：
顺接一次，反接一次，就可以测出互感：
L顺 L反 M 4
全耦合时
M L1L2
当 L=
L1=L2 时 , M=L
L L1 L2 2 M L1 L2 2 L1 L2 ( L1 L2 )
注意 耦合系数 k 与线圈的结构、相互几何位置、空
间磁介质有关。
返 回 上 页 下 页
互感现象
利用——变压器：信号、功率传递 避免——干扰
克服：合理布置线圈相互位置或增加屏蔽减少互感 作 用。
返 回
上 页
下 页
4. 耦合电感上的电压、电流关系
i2 2 M 当i1 为时变电流时，磁通也将随时间变化，从
用耦合系数k 表示两个线 圈磁耦合的紧密程度。
M 1 k L1L2
def
k=1 称全耦合: 漏磁 F 1 =F 2=0 满足：
k
def
F11= F21 ，F22 =F12

大学电路耦合电感电路(1)

大学电路耦合电感电路(1)








Leq L1 L2 2M
可见反接时等效电感减少！
两个有互感的线圈反接串联

反接串联时等效电感减少，说明反接 时有削弱电感的作用，互感的这种作 用称为互感的“容性”效应。在这种 效应的作用下可能会出现其中一个电 感小于互感M，但不可能都小，整个 电路仍呈感性。
21 M 21 i1 M 12 12 i2 M 21 M 12 M
耦合系数k
M k L1 L2

L1、L2为线圈1和线圈2的自感；M为两个 线圈的互感。 k 称为耦合系数，取值范 围为 0≤k≤1。 k的大小与线圈的结构、两 线圈的相对位置以及周围的磁介质有关。
k与线圈的相对位置有关
di1 di2 u1 L1 M dt dt di2 di1 u2 L2 M dt dt
令i1 2I1 cos(t 1 ) i2 2I 2 cos(t 2 )
U 1 jL1 I 1 jM I 2 U 2 jL2 I 2 jM I 1

可见顺接时等效电感增加！
2、反接串联
U U 1U 2 ( R1 jL1 ) I jM I ( R2 jL2 ) I jM I
[( R1 R2 ) j ( L1 L2 2 M )] I ( Req jLeq ) I Z eq I
如何确定互感元件的约束方程？
互感元件的电压中包含两部分电压，即自 感电压项uL1 、uL2和互感电压项uM1 、uM2 。 确定互感元件约束方程的方法如下： ① 如果两个线圈中的电流都是从同名端流入 （或流出），则自感电压项与互感电压项 同号；否则异号。 ② 如果线圈1的u1与i1为关联参考方向，则自 感电压项uL1为正，否则为负。线圈2的自 感电压项判断方法同上。

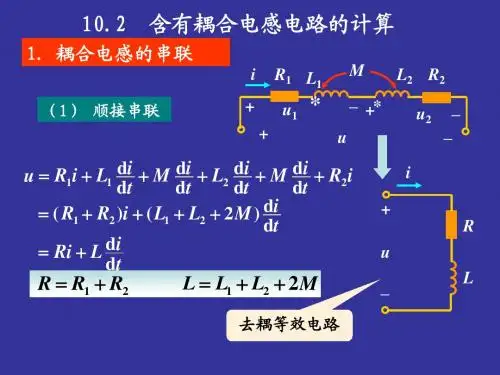
10.2含有耦合电感的电路

10.2 含有耦合电感电路的计算
1. 耦合电感的串联
i （1） 顺接串联 + + R1 L1 u1 M – +* u i + R u L – L2 R2 u2 – –
*
u = R i + L di + M di + L2 di + M di + R2i 1 1 dt dt dt dt = ( R + R2 )i + (L + L2 + 2M) di 1 1 dt = Ri + L di dt
求图示电路的开路电压。 例2 求图示电路的开路电压。
& I1 R1 • L1
∆
M12 L2 • *
解1
+
& US
+ _
M31
L3 M23 ∆ *
& Uoc
_
& US I1 = R + jω(L + L3 − 2M31) 1 1 & & & & & U0c = jωM12I1 − jωM23I1 − jωM31I1 + jωL3I1
•
I1
jω M * *
•
•
•
I2
2 jωL2
I1
I2
2 jω(L2-M) jωM 3
•
1 jω(L1-M)
1 jωL1
•
3
•
I
• • •
I
•
U13 = jωL I1 + jωM I 2 = jω L − M) I1 + jωM I ( 1 1 U23 = jωL2 I 2 + jωM I1 = jω L2 − M) I 2 + jωM I (

大学电路课件——08第八章含有耦合电感的电路和谐振电路


N1
i2
N2
+ u1 –
+ u2 –
12
22
11
i1
N1
i2
N2
+ u1 –
+ u2
1 11 12 11 自感磁链
2 21 22 22 自感磁链
21
–
12 互感磁链 21 互感磁链
12
22
11
i1
N1
21
N2
i2
1 11 12
+ u1 –
u2

M
di1 dt

L2
di2 dt
u1

L1
di1 dt

M
di2 dt
u2

M
di1 dt

L2
di2 dt

jM

I1
I2

U1
jL1

jL2 U 2

jM

I1
I2

U1
jL1

jL2 U 2
在正弦交流电路中，其相量形式的方程为



U 1 jL1 I 1 jM I 2
这种一个线圈的磁通交链另一线圈的现象称为磁耦合。
11：自感磁通
21 11
21：耦合磁通（互感磁通）
i1：施感电流
2、互感电压
当i1为时变电流时，磁通也将随时间变化，从而在线圈 两端产生感应电压。
11 21
i1变化
i1
N1
N2
+ u11 –
11变化 21变化
+ u21 – 电磁感应定律 和楞次定律 u11自感电压

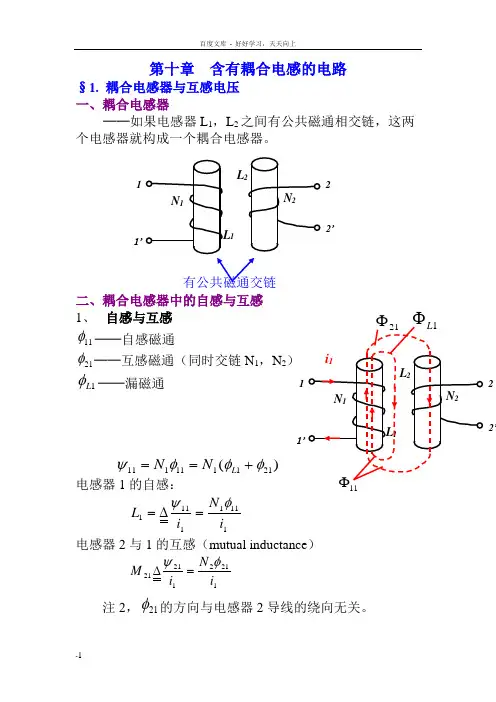
含有耦合电感的电路(学生用)

百度文库 - 好好学习，天天向上第十章 含有耦合电感的电路§1. 耦合电感器与互感电压 一、耦合电感器──如果电感器L 1，L 2之间有公共磁通相交链，这两个电感器就构成一个耦合电感器。

有公共磁通交链 二、耦合电感器中的自感与互感 1、 自感与互感 11φ──自感磁通21φ──互感磁通（同时交链N 1，N 2） 1L φ──漏磁通)(211111111φφφψ+==L N N电感器1的自感：11111111i N i L φψ=∆=电感器2与1的互感（mutual inductance ）121212121i N i M φψ=∆注2，21φ的方向与电感器2导线的绕向无关。

1 1’22’1 L 11’22’11电感器2的自感：22222222i N i L φψ=∆电感器1与2的互感212121212i N i M φψ=∆同样，12φ的方向与电感器1导线的绕向无关。

物理学中已证明。

M M M ∆=2112单位：亨利H 2. 耦合系数k──表明两个电感器之间磁耦合的紧密程度。

22211112ψψψψ⋅∆k21 L L M k =),,,(12121222221111Mi Mi i L i L ====ψψψψ1≤k1=k ──全耦合电感器（相当于021==L L φφ无漏磁通）实际中：当双线并绕时，耦合最强，1→k 。

当两个耦合电感器相距甚远，或彼此垂直时，其间耦合较弱，0→k 。

⎩⎨⎧><称强耦合时称弱耦合时,5.0,5.0k k 21112111Mi i L +=+=ψψψ 12221222Mi i L +=+=ψψψ表明：在该种绕线方式中，互感磁链与自感磁链方向一致，称为互感的“增助”作用。

改变电感器2的绕线方式：31113111Mi i L -=-=ψψψ 13331333Mi i L -=-=ψψψ表明：在这种绕线方式中，互感磁链与自感磁链方向相11’22’ΦΦ11’3’3ΦΦ反，称为互感的“削弱”作用。

第十章--含有耦合电感的电路


正值表示自感磁链与互感磁链方向一致，互感起
增助作用，负值表示自感磁链与互感磁链方向相 反，互感起削弱作用。
2024年7月17日星期
11
三
3. 同名端的概念及其判断方法！
通过线圈的绕向、 位置和施感电流的
F12
参考方向，用右手
螺旋法则，就可以 F11 判定互感是“增助”
还是“削弱” 。
但实际的互感线圈 往往是封闭的，看 不出绕向；
三
§10-1 互感
1. 互感的概念 一个电感线圈的情况
L1 N1
i1产生的磁通为F11。
i1与F11的参考方向符 F11
合右手螺旋法则，为
关联的参考方向。
i1
1' -
u11
1 +
F11穿越自身线圈时，
产生的自感磁通链用
若u11与i1取关联参考方向
Y11表示：Y11= L1i1
当i1变化时，将产生 自感电压u11。
第十章 含有耦合电感的电路
学习要点 熟练掌握互感的概念； 具有耦合电感电路的计算方法：
①直接列写方程的支路法或回路法。 ②受控源替代法。 ③互感消去法。 掌握空心变压器和理想变压器的应用。
2024年7月17日星期
1
三
重点
互感和互感电压的概念及同名端的含义； 含有互感电路的计算； 空心变压器和理想变压器的电路模型。
名端要用不同的符号一对一对标记。
L2
M
L1 *
* L2
2'பைடு நூலகம்
1 i1
+
M
i2 2
+
M
L3 M
u1
-
L1
1'
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十章 含有耦合电感的电路
§1. 耦合电感器与互感电压 一、耦合电感器
──如果电感器L 1，L 2之间有公共磁通相交链，这两个电感器就构成一个耦合电感器。

1、11φ21φ1L φ
电感器2与1的互感（mutual inductance ）
1
21
212121i N i M φψ=∆
注2，21φ的方向与电感器2导线的绕向无关。

2
2’
1=k ──全耦合电感器（相当于021==L L φφ无漏磁通） 实际中：
当双线并绕时，耦合最强，1→k 。

当两个耦合电感器相距甚远，或彼此垂直时，其间耦合较弱，0→k 。

⎩
⎨⎧><称强耦合时称弱耦合时,5.0,5.0k k
1ψ2ψ
1ψ13331333Mi i L -=-=ψψψ
表明：在这种绕线方式中，互感磁链与自感磁链方向相反，称为互感的“削弱”作用。

ΦΦ3’
3
问题：在电路分析中，在确定互感电压时，是否一定要知道耦合电感器的实际绕向呢？
同名端──在耦合电感器各自一个端钮上通进电流，如果它们产生的互感磁通同方向，这两个端钮就称为同名端。

在同名端上打上标记“。

”、“.”、“*”或“∆”均可。

标有同名端，并用参数表示的耦合电感器的电路符号为：
3.
21i i 、为时变函数时：
dt di M dt di L dt Mi i L d dt d u 2
1121111)(+=+==ψ
dt
di M dt di L dt Mi i L d dt d u 1
2212222)(+=+==ψ
当21i i 、为同频率正弦量时，在正弦稳态情况下：
2
111I M j I L j U ωω+=∙
1
222I M j I L j U ωω+=∙
M ω──互感抗
开关S 闭合瞬间，若直流微安表正偏，表明端钮1与2为同名端。

1 2’ ∙
例：已知：tA i H M H L H L R s sin 210,5.0,2,1,1211====Ω= 试确定稳态开路电压u oc 。

∴ V t u oc )135sin(5︒-=
§2 含有耦合电感器的电路的计算
一、耦合电感器的串联
u1
u1
二、耦合电感的并联──去耦合等值电路
对
即
将i
思考：1. 电压u 12有无改变？
2. 通过去耦合等值电路确定电感器顺、反串时的等值电
感？
注乙几个问题：
① 只有当耦合电感器有一端相接时，才有其去耦合等值电
I == 分流： A j I M
j M L j M j I 2122
)(=-+-= ωωω
A j I I I 6213-=-=
时域电流为 A t i )90sin(241︒-=
A t i )90sin(222︒+=
A t i )90sin(263︒-=
例2 计算图中的电流1∙
I 、2∙
I。