一次函数的图象与性质

一次函数的定义和性质一次函数是指形如y=ax+b的函数，其中a和b为常数，且a不等于零。

它也被称为线性函数，因为它的图像是一条直线。

一次函数是数学中的基础概念之一，具有一些重要的性质和应用。

一. 定义一次函数是指以x为自变量，以y为因变量的函数，其表达式为y=ax+b，其中a和b为实数，且a不等于零。

其中，a称为一次项的系数，b称为常数项。

当x取不同的值时，y的取值也相应地发生变化，这种对应关系可以通过一条直线来表示。

二. 图像特征1. 直线特征：一次函数的图像总是一条直线，因此它具有线性特征；2. 斜率特征：一次函数的斜率表示为常数a，描述了图像在x轴正方向上的倾斜程度。

斜率为正时，表示图像向上倾斜；斜率为负时，表示图像向下倾斜；3. 截距特征：一次函数的截距表示为常数b，描述了图像与y轴的交点位置。

截距为正时，表示图像与y轴正半轴交于正值点；截距为负时，表示图像与y轴负半轴交于负值点。

三. 性质1. 单调性：一次函数的单调性由斜率的正负决定。

当a大于零时，函数单调递增；当a小于零时，函数单调递减；2. 定义域和值域：一次函数的定义域为所有实数；值域为所有实数，即函数的取值范围没有限制；3. 零点：一次函数的零点即为函数的根，表示当x取某个值时，函数的值等于零。

对于一次函数，当且仅当x=-b/a时，函数的值为零；4. 最值：一次函数没有最大值和最小值，因为它的图像是一条直线；5. 平移：通过给定一次函数的表达式，可以进行平移操作来得到新的函数。

平移操作可以在x轴和y轴上分别进行，通过改变常数a和b的值，可以使图像在平面上发生移动。

四. 应用一次函数在现实生活中有着广泛的应用，例如：1. 财务收入：一些经济指标和统计数据的变化趋势可以通过一次函数来表示，如年度收入的增长率；2. 运动模型：一次函数可以表示一些常见的运动模型，如匀速运动的位移和速度关系；3. 经济学模型：在经济学中，一次函数可以用来表示供求关系、成本和收益关系等；4. 工程预测：一次函数可以用来进行工程测量、预测物理量的变化趋势等。

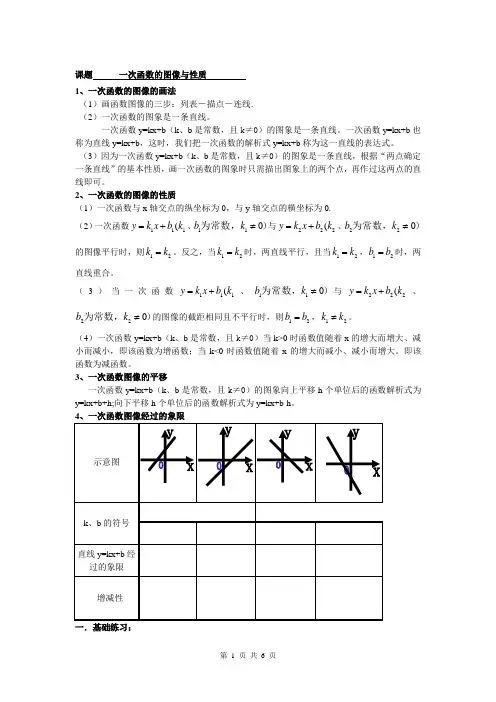
课题 一次函数的图像与性质1、一次函数的图像的画法（1）画函数图像的三步：列表－描点－连线. （2）一次函数的图象是一条直线。

一次函数y=kx+b （k 、b 是常数，且k ≠0）的图象是一条直线。

一次函数y=kx+b 也称为直线y=kx+b ，这时，我们把一次函数的解析式y=kx+b 称为这一直线的表达式。

（3）因为一次函数y=kx+b （k 、b 是常数，且k ≠0）的图象是一条直线，根据“两点确定一条直线”的基本性质，画一次函数的图象时只需描出图象上的两个点，再作过这两点的直线即可。

2、一次函数的图像的性质（1）一次函数与x 轴交点的纵坐标为0，与y 轴交点的横坐标为0.（2）一次函数111(y k x b k =+、110b k ≠为常数，）与222(y k x b k =+、220b k ≠为常数，）的图像平行时，则12k k =。

反之，当12k k =时，两直线平行，且当12k k =，12b b =时，两直线重合。

（3）当一次函数111(y k x b k =+、110b k ≠为常数，）与222(y k x b k =+、220b k ≠为常数，）的图像的截距相同且不平行时，则12b b =，12k k ≠。

（4）一次函数y=kx+b （k 、b 是常数，且k ≠0）当k>0时函数值随着x 的增大而增大、减小而减小，即该函数为增函数；当k<0时函数值随着x 的增大而减小、减小而增大。

即该函数为减函数。

3、一次函数图像的平移一次函数y=kx+b （k 、b 是常数，且k ≠0）的图象向上平移h 个单位后的函数解析式为y=kx+b+h;向下平移h 个单位后的函数解析式为y=kx+b-h 。

4、一次函数图像经过的象限示意图k 、b 的符号直线y=kx+b 经过的象限增减性一．基础练习：1.一次函数y=3x-6的图像是，它与x轴的交点坐标是，它与y轴的交点坐标是2.将直线y=x向下平移4个单位，得到直线3.将直线y=-3x-5向上平移4个单位，得到直线4.若直线y=3x-5与直线y=kx-4相互平行，则k=5.若直线y=-2x-5与直线y=6x+b相交于y轴上同一点，则b=6. 请你在不同的平面直角坐标系中画出下列函数的图像（1）y=2x+6 （2）1722 y x=+（3）4833y x=--（4）1344y x=--7,做一做：画出函数y=-2x+2 的图像，结合图象回答下列问题：（ 1 ）这个函数中，随着x 的增大，y 将增大还是减小？（ 2 ）当x 取何值时，y=0 ？当y 取何值时，x=0 ？（ 3 ）当x 取何值时，y>0 ？（ 4 ）函数的图像不经过哪个象限？8、完成下列各题：（1）下列函数中，y的值随着x的增大而减小的是（）A.y=2x-7B.y=0.5x+2C.y=(2-1)x+3D.y=-0.3x+1（2）函数y=4x-3中，y的值随着x值的增大而____（3）函数y=(2m-1)x+2的函数值随x的增大而减小，则m的值为______ （4）一次函数y=2x+4的图像上有两点A(3,a)，B(4,b)，请判断a与b的大小（5）y=x+5与y=2x-5的增减性（y 随着x 的增加而增加，还是随着x 的增加而减小）是否一样？（6）y=-2x+5与y=-2x-5的增减性是否一样？（7）A(a,6)和B(b,-2)在函数y=2x-5的图像上，请你判断a ，b 的大小关系 9、已知一次函数2(2)28y k x k =--+，分别根据下列条件求k 的值或k 的取值范围： （1）它的图像经过原点（2）它的图像经过点（0,－2）（3）它的图像与y 轴的交点在x 轴上方 （4）y 随着x 的增大而减小（5）这条直线经过一、二、三象限10、要使一次函数y=-3x+4的函数值大于4，求自变量x 的取值范围。

一次函数图像性质
一次函数图像性质
1.y=kx时(即b等于0，y与x成正比，此时的图象是一条经过原点的直线)
当k>0时，直线必通过一、三象限，y随x的增大而增大;
当k<0时，直线必通过二、四象限，y随x的增大而减小。

2.y=kx+b(k,b为常数，k≠0)时：
当k>0,b>0,这时此函数的图象经过一，二，三象限;
当k>0,b<0,这时此函数的图象经过一，三，四象限;
当k<0,b>0,这时此函数的图象经过一，二，四象限;
当k<0,b<0,这时此函数的图象经过二，三，四象限。

当b>0时，直线必通过一、二象限;
当b<0时，直线必通过三、四象限。

特别地，当b=0时，直线通过原点O(0，0)表示的是正比例函数的图象。

这时，当k>0时，直线只通过一、三象限，不会通过二、四象限。

当k<0时，直线只通过二、四象限，不会通过一、三象限。

3.直线y=kx+b中k、b的关系
k>0,b>0：经过第一、二、三象限
k>0,b<0：经过第一、三、四象限
k>0,b=0：经过第一、三象限(经过原点)
结论：k>0时，图象从左到右上升，y随x的增大而增大。

k<0b>0：经过第一、二、四象限
k<0,b<0：经过第二、三、四象限
k<0,b=0：经过第二、四象限(经过原点)
结论：k<0时，图象从左到右下降，y随x的增大而减小。

一次函数的图像和性质一次函数是一个代数函数，也称为线性函数或直线函数。

它是最简单的一种函数形式，在数学和物理等领域中都有广泛的应用。

一次函数的一般形式为y = ax + b，其中a和b是常数，且a≠0。

一次函数的图像是一个直线，在平面直角坐标系中表示为一根斜率为a的直线，并且通过点(0,b)。

斜率a表示函数的变化率，即y随x的变化速度。

当a>0时，表明随着x增大，y也增大；当a<0时，表明随着x增大，y减小；当a=0时，函数是一个常数函数。

一次函数图像的性质包括斜率、截距、与坐标轴的交点等。

1.斜率：一次函数的斜率表示函数图像在x轴方向每单位变化时，y轴方向的变化量。

斜率的计算可以通过选择两个不同的x值，计算对应的y值的差异，然后除以对应x值的差异。

即斜率a=Δy/Δx。

斜率为正的函数图像向上倾斜，斜率为负的函数图像向下倾斜，斜率为零的函数图像是水平的。

2. 截距：一次函数的截距表示函数图像与y轴的交点，它的值可以从函数的形式y=ax+b中得到。

当x=0时，y=b，因此截距为b。

3. 与坐标轴的交点：一次函数的图像与x轴的交点为y=0时的x值，可以通过令y=0，解方程ax+b=0，得到x=-b/a。

图像与y轴的交点已经在上述截距部分提到，为(0, b)。

4.平行：两个斜率相等的一次函数图像是平行的，它们可能在坐标轴上的交点不同，但是平行于同一直线。

5. 垂直平分线：对于一次函数y = ax + b，它的垂直平分线为x =-a/2、如果两个函数的图像关于该直线对称，那么它们是互为反函数。

6. 对称轴：对于一次函数y = ax + b，它的对称轴为x = -b/(2a)。

如果交换a和b的位置，可以得到该函数关于y轴对称函数。

如果交换x和y的位置，可以得到原函数的倒数。

7.等差数列：一次函数的图像可以表示等差数列，其中公差为斜率a。

数列的第一个项为截距b。

8.增长率：一次函数的增长率等于斜率a的绝对值。

一次函数的图象和性质一、知识要点：1、一次函数：若两个变量x,y存在关系为y=kx+b (k≠0, k,b为常数)的形式，则称y是x的函数。

注意：（1）k≠0,否则自变量x的最高次项的系数不为1；（2）当b=0时，y=kx，y叫x的正比例函数。

2、图象：一次函数的图象是一条直线（1）两个常有的特殊点：与y轴交于（0，b）；与x轴交于（- ，0）。

（2）正比例函数y=kx(k≠0)的图象是经过（0，0）和（1，k）的一条直线；一次函数y=kx+b(k≠0)的图象是经过（- ，0）和（0，b）的一条直线。

（3）由图象可以知道，直线y=kx+b与直线y=kx平行，例如直线：y=2x+3与直线y=2x-5都与直线y=2x平行。

3、一次函数图象的性质：（1）图象在平面直角坐标系中的位置:（2）增减性：k>0时，y随x增大而增大；k<0时，y随x增大而减小。

4、求一次函数解析式的方法求函数解析式的方法主要有三种：一是由已知函数推导，如例题1；二是由实际问题列出两个未知数的方程，再转化为函数解析式，如例题4的第一问。

三是用待定系数法求函数解析式，如例2的第二小题、例7。

其步骤是：①根据题给条件写出含有待定系数的解析式；②将x、y的几对值或图象上几个点的坐标代入上述的解析式中，得到以待定系数为未知数的方程或方程组；③解方程，得到待定系数的具体数值；④将求出的待定系数代入要求的函数解析式中。

二、例题举例：例1、已知变量y与y1的关系为y=2y1,变量y1与x的关系为y1=3x+2，求变量y与x的函数关系。

分析：已知两组函数关系，其中共同的变量是y1,所以通过y1可以找到y与x 的关系。

解：∵y=2y1y1=3x+2,∴y=2(3x+2)=6x+4,即变量y与x的关系为：y=6x+4。

例2、解答下列题目（1）（甘肃省中考题）已知直线与y轴交于点A，那么点A的坐标是（）。

（A）（0，–3）（B）（C）（D）（0，3）（2）(杭州市中考题)已知正比例函数，当x=–3时，y=6．那么该正比例函数应为（）。

一次函数的图像与性质一次函数，也被称为线性函数，是指一个变量与另一个变量之间的关系可以表示为 y = ax + b 的函数形式，其中 a 和 b 是常数。

本文将探讨一次函数的图像及其相关性质。

I. 一次函数的图像一次函数的图像是一条直线，在直角坐标系中表示为一条斜率为a、截距为 b 的直线。

斜率 a 决定了直线的倾斜方向和角度。

若 a > 0，则直线向右上方倾斜；若 a < 0，则直线向右下方倾斜；若 a = 0，则直线为水平直线。

截距 b 则表示了直线与 y 轴的交点。

II. 一次函数的性质1. 斜率一次函数的斜率 a 表示了直线的倾斜程度。

斜率的绝对值越大，则直线越陡峭；斜率为正值时表示直线上升，为负值时表示直线下降；斜率为零时表示直线水平。

通过斜率，我们可以判断一次函数的增减性。

2. 截距截距 b 表示了一次函数与 y 轴的交点，即当 x = 0 时，函数的取值。

截距的正负决定了直线在 y 轴上的位置，正值表示与 y 轴正向交点在上方，负值则在下方。

截距的大小也影响了直线与坐标轴的交点。

3. 零点一次函数的零点是指函数取值为零的点，也就是使得y = 0 的x 值。

通过求解一次函数的零点，我们可以求得函数与 x 轴的交点。

4. 增减性一次函数的增减性由斜率来决定。

当斜率a > 0 时，函数单调递增；当斜率 a < 0 时，函数单调递减；当斜率 a = 0 时，函数为常数函数，不具有增减性。

5. 定义域与值域一次函数的定义域为所有实数，因为 x 可以取任意实数值；值域则由斜率和截距来决定。

当斜率 a > 0 时，值域为 (-∞, +∞)；当斜率 a < 0 时，值域为(+∞, -∞)；当斜率 a = 0 时，值域只有截距 b。

6. 图像平移一次函数的图像可以通过改变斜率或截距来进行平移变换。

增加或减小截距 b 可以使得图像上下平移，增加或减小斜率 a 则使得图像左右平移。

考点三一次函数的图像与性质知识点整合一、正比例函数的概念一般地，形如y=kx（k是常数，k≠0）的函数，叫做正比例函数，其中k叫做正比例系数．二、一次函数1.一次函数的定义一般地，形如y=kx+b(k，b为常数，且k≠0)的函数叫做x的一次函数.特别地，当一次函数y=kx+b中的b=0时，y=kx（k是常数，k≠0）．这时，y叫做x的正比例函数．2.一次函数的一般形式一次函数的一般形式为y=kx+b，其中k，b为常数，k≠0．一次函数的一般形式的结构特征：（1）k≠0，（2）x的次数是1；（3）常数b可以为任意实数.3.注意（1）正比例函数是一次函数，但一次函数不一定是正比例函数.（2）一般情况下，一次函数的自变量的取值范围是全体实数.（3）如果一个函数是一次函数，则含有自变量x的式子是一次的，系数k不等于0，而b可以为任意实数．（4）判断一个函数是不是一次函数，就是判断它是否能化成y=kx+b（k≠0）的形式.（5）一次函数的一般形式可以转化为含x、y的二元一次方程.三、一次函数的图象及性质1．正比例函数的图象特征与性质正比例函数y=kx（k≠0）的图象是经过原点（0，0）的一条直线．k的符号函数图象图象的位置性质k>0图象经过第一、三象限y随x的增大而增大k<0图象经过第二、四象限y随x的增大而减小2.一次函数的图象特征与性质（1）一次函数的图象一次函数的图象一次函数y=kx+b(k≠0)的图象是经过点(0，b)和(-b k，0)的一条直线图象关系一次函数y=kx+b(k≠0)的图象可由正比例函数y=kx(k≠0)的图象平移得到；b>0，向上平移b个单位长度；b<0，向下平移|b|个单位长度图象确定因为一次函数的图象是一条直线，由两点确定一条直线可知画一次函数图象时，只要取两点即可（2）一次函数的性质函数字母取值图象经过的象限函数性质y=kx+b(k≠0)k>0，b>0一、二、三y随x的增大而增大k>0，b<0一、三、四y=kx+b(k≠0)k<0，b>0一、二、四y随x的增大而减小k<0，b<0二、三、四3.k，b的符号与直线y=kx+b（k≠0）的关系在直线y=kx+b（k≠0）中，令y=0，则x=-bk，即直线y=kx+b与x轴交于（–bk，0）．①当–bk>0时，即k，b异号时，直线与x轴交于正半轴．②当–bk=0，即b=0时，直线经过原点．③当–bk<0，即k，b同号时，直线与x轴交于负半轴．4.两直线y=k1x+b1（k1≠0）与y=k2x+b2（k2≠0）的位置关系：①当k1=k2，b1≠b2，两直线平行；②当k1=k2，b1=b2，两直线重合；③当k1≠k2，b1=b2，两直线交于y轴上一点；④当k1·k2=–1时，两直线垂直．四、待定系数法1．定义：先设出函数解析式，再根据条件确定解析式中未知数的系数，从而得出函数解析式的方法叫做待定系数法．2．待定系数法求正比例函数解析式的一般步骤（1）设含有待定系数的函数解析式为y=kx（k≠0）．（2）把已知条件（自变量与函数的对应值）代入解析式，得到关于系数k的一元一次方程．（3）解方程，求出待定系数k．（4）将求得的待定系数k的值代入解析式．3．待定系数法求一次函数解析式的一般步骤（1）设出含有待定系数k、b的函数解析式y=kx+b．（2）把两个已知条件（自变量与函数的对应值）代入解析式，得到关于系数k，b的二元一次方程组．（3）解二元一次方程组，求出k，b．（4）将求得的k，b的值代入解析式．五、一次函数与正比例函数的区别与联系正比例函数一次函数区别一般形式y=kx+b（k是常数，且k≠0）y=kx+b（k，b是常数，且k≠0）图象经过原点的一条直线一条直线k，b符号的作用k的符号决定其增减性，同时决定直线所经过的象限k的符号决定其增减性；b的符号决定直线与y轴的交点位置；k，b的符号共同决定直线经过的象限求解析式的条件只需要一对x，y的对应值或一个点的坐标需要两对x，y的对应值或两个点的坐标联系比例函数是特殊的一次函数．②正比例函数图象与一次函数图象的画法一样，都是过两点画直线，但画一次函数的图象需取两个不同的点，而画正比例函数的图象只要取一个不同于原点的点即可．③一次函数y=kx+b（k≠0）的图象可以看作是正比例函数y=kx（k≠0）的图象沿y 轴向上（b>0）或向下（b<0）平移|b|个单位长度得到的．由此可知直线y=kx+b（k≠0，b≠0）与直线y=kx（k≠0）平行．④一次函数与正比例函数有着共同的性质：a．当k>0时，y的值随x值的增大而增大；b．当k<0时，y的值随x值的增大而减小．六、一次函数与方程（组）、不等式1．一次函数与一元一次方程任何一个一元一次方程都可以转化为kx+b=0(k，b为常数，且k≠0)的形式．从函数的角度来看，解这个方程就是寻求自变量为何值时函数值为0；从函数图象的角度考虑，解这个方程就是确定直线y=kx+b与x轴的交点的横坐标．2．一次函数与一元一次不等式任何一个一元一次不等式都能写成ax+b>0（或ax+b<0）（a，b为常数，且a≠0）的形式．从函数的角度看，解一元一次不等式就是寻求使一次函数y=ax+b（a≠0）的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=ax+b（a≠0）在x轴上（或下）方部分的点的横坐标满足的条件．3．一次函数与二元一次方程组一般地，二元一次方程mx+ny=p（m，n，p是常数，且m≠0，n≠0）都能写成y=ax+b（a，b为常数，且a≠0）的形式．因此，一个二元一次方程对应一个一次函数，又因为一个一次函数对应一条直线，所以一个二元一次方程也对应一条直线．进一步可知，一个二元一次方程对应两个一次函数，因而也对应两条直线．从数的角度看，解二元一次方程组相当于考虑自变量为何值时，两个函数的值相等，以及这两个函数值是何值；从形的角度看，解二元一次方程组相当于确定两条直线的交点坐标，一般地，如果一个二元一次方程组有唯一解，那么这个解就是方程组对应的两条直线的交点坐标．考向一一次函数和正比例函数的定义1．正比例函数是特殊的一次函数．2．正比例函数解析式y=kx（k≠0）的结构特征：①k≠0；②x的次数是1．典例引领二、填空题变式拓展6．已知y 与1x +成正比，当1x =时，2y =．考向二一次函数的图象及性质1．通常画正比例函数y=kx（k≠0）的图象时只需取一点（1，k），然后过原点和这一点画直线．2．当k>0时，函数y=kx（k≠0）的图象从左向右，呈上升趋势；当k<0时，函数y=kx（k≠0）的图象从左向右，呈下降趋势．3．正比例函数y=kx中，|k|越大，直线y=kx越靠近y轴；|k|越小，直线y=kx越靠近x轴．4．一次函数图象的位置和函数值y的增减性完全由b和比例系数k的符号决定．典例引领【答案】A【分析】本题考查的是一次函数的性质．根据一次函数的性质以及图像上点的坐标特征对各选项进行逐一判断即可．【详解】解：A 、当0x =时，2y =，图象必经过点()0,2，故本选项符合题意；B 、∵10k =-<，20b =>，∴图象经过第一、二、四象限，故本选项不符合题意；C 、∵10k =-<，∴y 随x 的增大而减小，故本选项不符合题意；D 、∵y 随x 的增大而减小，当2x =-时，0y =，∴当2x >时，0y <，故本选项不符合题意；故选：A ．4．若一次函数21y x =-+的图象经过点()13,y -，()24,y ，则1y 与2y 的大小关系（）A ．12y y <B ．12y y >C ．12y y ≤D ．12y y ≥【答案】B【分析】本题主要考查了比较一次函数值的大小，根据函数解析式得到y 随x 增大而减小，据此可得答案．【详解】解：∵一次函数解析式为21y x =-+，20-<，∴y 随x 增大而减小，∵一次函数21y x =-+的图象经过点()13,y -，()24,y ，34-<，∴12y y >，故选：B ．5．已知一次函数(2)=-+y k x k ，且y 随x 的增大而减小，则k 的取值范围是（）A ．2k >B ．0k <C ．2k <D ．2k ≤【答案】C【分析】此题主要考查一次函数的性质，根据一次函数的增减性即在y kx b =+中，k >0时y 随x 的增大而增大；k <0时，y 随x 的增大而减小即可求解．【详解】依题意得20k -<，解得2k <故选C ．变式拓展三、解答题9．已知一次函数(2)312y k x k =--+．(1)k 为何值时，函数图象经过点(0,9)？(2)若一次函数(2)312y k x k =--+的函数值y 随x 的增大而减小，求k 的取值范围．【答案】(1)1(2)2k <【分析】（1）将点(0,9)代入一次函数(2)312y k x k =--+，可得关于k 的一元一次方程，求解即可获得答案；（2）根据该函数的增减性，可得20k -<，求解即可获得答案．【详解】（1）解：将点(0,9)代入一次函数(2)312y k x k =--+，可得3129k -+=，解得1k =，∴当1k =时，函数图象经过点(0,9)；（2）若一次函数(2)312y k x k =--+的函数值y 随x 的增大而减小，则有20k -<，解得2k <，∴k 的取值范围为2k <．【点睛】本题主要考查了求一次函数解析式、根据一次函数的增减性求参数、解一元一次方程和解一元一次不等式等知识，熟练掌握一次函数的图象与性质是解题关键．10．已知2y -与x 成正比，且当2x =-时，8y =．(1)求y 与x 的函数关系式；(2)当x 取什么范围时，4y >-．【答案】(1)32y x =-+(2)2x <【分析】本题考查待定系数法求解析式，一次函数图象及性质．（1）设y 与x 的函数关系式为2y kx -=，再待定系数法求解即可；（2）利用一次函数图象及性质，代入4y =-后即可得到本题答案．【详解】（1）解：设y 与x 的函数关系式为2y kx -=，将当2x =-时，8y =代入2y kx -=中得：822k -=-，即：3k =-，∴32y x =-+；（2）解：∵32y x =-+，∴30k =-<，y 随x 增大而减小，当4y =-时，432x -=-+，即：2x =，∴4y >-时，2x <，综上所述：当2x <时，4y >-．考向三用待定系数法确定一次函数的解析式运用待定系数法求一次函数解析式的步骤可简单记为：一设，二代，三解，四回代．典例引领1．《国务院关于印发全民健身计划（2021-2025年）的通知》文件提出，加大全民健身场地设施供给，建立健全场馆运营管理机制，提升场馆使用效益．某健身中心为答谢新老顾客，举行大型回馈活动，特推出两种“冬季唤醒计划”活动方案．方案1：顾客不购买会员卡，每次健身收费30元．方案2：顾客花200元购买会员卡，每张会员卡仅限本人使用一年，每次健身收费10元．设王彬一年内来此健身中心健身的次数为x （次），选择方案1的费用为1y （元），选择方案2的费用为2y （元）．(1)分别写出1y ，2y 与x 之间的函数关系式；(2)在如图的平面直角坐标系中分别画出它们的函数图象；(3)预计王彬一年内能来此健身中心12次，选择哪种方案比较合算？并说明理由．【答案】(1)130y x =，210200y x =+(2)见解析(3)他选择方案二比较合算，理由见解析【分析】（1）本题主要考查了列函数关系式，根据两种方案分别列出函数关系式即可，理解题意是解题的关键；（2）本题主要考查了画函数图像，分别确定两个函数图像上的两个点，然后连接即可；理解函数图像上的点满足函数解析式是解题的关键；（2）本题主要考查了不等式的应用，解不等式3010200x x <+，即可确定来此健身中心12次费用较小的方案．正确求解不等式是解题的关键．【详解】（1）解：根据题意得：130y x =，210200y x =+；所以12y y ，与x 之间的函数表达式分别为130y x =，210200y x =+．（2）解：当0x =时，10y =，2200y =；当4x =时，1120y =，2240y =．据此描点、连线画出函数图像如下：（3）解：王斌择方案二比较合算，理由如下：解不等式3010200x x >+，解得：10x >，所以当10x >时，方案二优惠，因为1210>，王斌择方案二比较合算．2．已知4y +与3x -成正比例，且1x =时，0y =(1)求y 与x 的函数表达式；(2)点(1,2)M m m +在该函数图象上，求点M 的坐标．【答案】(1)22y x =-+(2)点M 的坐标为(1,0)【分析】（1）利用正比例函数的定义，设4y +=(3)k x -，然后把已知的对应值代入求出k 即可；（2）把(1,2)M m m +代入（1）中的解析式得到关于m 的方程，然后解方程即可．【详解】（1）设y 与x 的表达式为4(3)y k x +=-，把1x =时，0y =代入4(3)y k x +=-得24k -=，解得2k =-，由题意，得52024x x ≥⎧⎨-≥⎩，解这个不等式组，得58x ≤≤，因为x 为整数，所以x 的值为5，6，7，8．所以安排方案有4种：方案一：装运食品5辆、药品10辆，生活用品5辆；方案二：装运食品6辆、药品8辆，生活用品6辆；方案三：装运食品7辆、药品6辆，生活用品7辆；方案四：装运食品8辆、药品4辆，生活用品8辆．【点睛】本题考查了列出实际问题中的函数关系式和一元一次不等式组的应用，正确理解题意、列出函数关系式和不等式组是解题的关键．5．习主席在二十大报告中提到“中国人的饭碗必须牢牢掌握在咱们自己手中”．为优选品种，提高产量，某农业科技小组对甲、乙两个水稻品种进行种植对比实验研究．去年甲、乙两个品种各种植了100亩，收获后甲、乙两个品种的售价均为2.8元/千克，且甲的平均亩产量比乙的平均亩产量低100千克，甲、乙两个品种全部售出后总收入为644000元．(1)请求出甲、乙两个品种去年平均亩产量分别是多少；(2)今年，科技小组加大了水稻种植的科研力度，在甲、乙种植亩数不变的情况下，预计甲、乙两个品种平均亩产量将在去年的基础上分别增加20x 千克和10x 千克．由于甲品种深受市场的欢迎，预计售价将在去年的基础上每千克上涨0.05x 元，而乙品种的售价将在去年的基础上每千克下降0.1x 元．若甲、乙两个品种全部售出后总收入为y 元，请写出y 与x 的关系式；若今年甲、乙两个品种全部售出后总收入比去年增加9500元，水x 的值．【答案】(1)甲水稻品种去年平均亩产量是1100千克，乙水稻品种去年平均亩产量是1200千克(2)x 的值为5【分析】（1）设甲水稻品种去年平均亩产量是m 千克，乙水稻品种去年平均亩产量是n 千克，根据：甲的平均亩产量比乙的平均亩产量低100千克，甲、乙两个品种全部售出后总收入为644000元，即可求解；（2）根据总收入等于甲乙两个品种的收入之和即可列出y 与x 的关系式，进而得到关于x 的方程，解方程即得答案．【详解】（1）设甲水稻品种去年平均亩产量是m 千克，乙水稻品种去年平均亩产量是n 千克，根据题意得1002.8100 2.8100644000n m m n -=⎧⎨⨯+⨯=⎩，解得m 11001200n =⎧⎨=⎩．答：甲水稻品种去年平均亩产量是1100千克，乙水稻品种去年平均亩产量是1200千克．（2）根据题意得：()()()()2.80.0510******* 2.80.1100120010y x x x x =+⨯++-⨯+，整理得1900644000y x =+，∴y 与x 的关系式1900644000y x =+．∵今年甲、乙两个品种全部售出后总收入比去年增加9500元，可得6440095001900644000x +=+，解得5x =．答：x 的值为5．【点睛】本题考查了二元一次方程组的应用，列出实际问题中的函数关系式，正确理解题意、找准相等关系是解题的关键．变式拓展c<时，如图2．②当0综上所述，d的取值范围是t≥时：当x t=时，①当0之间的关系如图所示．(1)求出图中a 、b 、c 的值；(2)在乙出发多少秒后，甲、乙两人相距60米？【答案】(1)8a =，92b =，123c =；(2)乙出发68秒或者108秒后，甲、乙两人相距60米．【分析】（1）由函数图象可以分别求出甲的速度为4米/秒，乙的速度为5米/秒，就可以求出乙追上甲的时间a 的值，b 表示甲跑完全程时甲、乙之间的距离，c 表示乙出发后多少时间，甲走完全程就用甲走完全程的时间−2就可以得出结论；（2）分别求出8秒到100秒和100秒到123秒的解析式，再把60y =代入即可解出x 值．【详解】（1）解：由题意及函数图象可以得出：甲的速度为：824÷＝（米/秒），乙的速度为：500÷100＝5（米/秒），8548a ÷-＝（）＝（秒）；500410292b -⨯＝＝（米），50042123c ÷-＝＝（秒），所以8,92,123a b c ===．（2）设8~100秒和100~123秒的解析式分别为11y k x b =+和22y k x b =+，把()()8010092，、，代入11y k x b =+得11110892100k b k b =+⎧⎨=+⎩解得1118k b =⎧⎨=-⎩，把()()123010092，、，代入22y k x b =+得2222012392100k b k b =+⎧⎨=+⎩解得224492k b =-⎧⎨=⎩，8~100秒解析式：8y x =-，100~123秒的解析式4492y x =-+，当60y =时，则68108x =或者，所以在乙出发68秒或者108秒后，甲、乙两人相距60米∵0＜x ≤1000，∴860≤x ≤1000．故答案为：y 1＝0.5x ；y 2＝0.3x +40；0＜x ≤200；200≤x ≤860；860≤x ≤1000．（2）根据题意可得，推出优惠活动后，y 1＝0.5a +0.25（x ﹣a ）＝0.25x +0.25a ，则有，0.257000.250.3700400.258600.250.386040a a ⎧⨯+≥⨯+⎨⨯+≤⨯+⎩解得300≤a ≤332．∴此时a 的取值范围为：300≤a ≤332．【点睛】本题主要考查了一元一次不等式组的应用，明确题意，列出不等式组是解题的关键．考向四一次函数与方程、不等式1．方程ax +b =k （a ≠0）的解⇔函数y =ax +b （a ≠0）中，y =k 时x 的值.2．方程ax +b =k （a ≠0）的解⇔函数y =ax +b （a ≠0）的图象与直线y =k 的交点的横坐标．3.一次函数y =ax +b （a ≠0）与一元一次不等式ax +b >0（或ax +b <0）的关系：ax +b >0的解集⇔y =ax +b 中，y >0时x 的取值范围，即直线y =ax +b 在x 轴上方部分图象对应的x 的取值范围；4.ax +b <0的解集⇔y =ax +b 中，y <0时x 的取值范围，即直线y =ax +b 在x 轴下方部分图象对应的x 的取值范围．5．二元一次方程kx -y +b =0（k ≠0）的解与一次函数y =kx +b （k ≠0）的图象上的点的坐标是一一对应的．6．两个一次函数图象的交点坐标，就是相应二元一次方程组的解，体现了数形结合的思想方法．典例引领1．直线1l ：1y kx b =+过点()0,4A 和()1,3D ，直线2l ：225y x =-和y 轴交于点B 和直线1l 交于C 点．(1)求两条直线交点C 的坐标及ABC 的面积；(2)x 取何值时，120y y >>．∵()0,4A ，()0,5B -，()3,1C ，∴9AB =，3CN =，∴112793222ABC S AB CN =⋅=⨯⨯= ．（2）∵14y x =-+，225y x =-，∴当120y y >>时，4250x x -+>->，解得：532x <<．2．已知直线443y x =-+与x 轴，y 轴分别交于点且把AOB 分成两部分．(1)若AOB 被分成的两部分面积相等，求k 与b ；⎩3．如图，在平面直角坐标系中，直线轴于点C和点D，两条直线交于点(1)求点A的坐标；(2)在直线CD上求点M【答案】(1)点A的坐标为(2)点M的坐标为44⎛∵3ABC MAB S S = ，∴23MBC ABC S S =△△，∵12ABC A S BC y =⋅△，121∵3ABC MAB S S = ，∴43MBC ABC S S =△△，(1)求点C的坐标；(2)求AOB的面积；(3)点D在直线122y x =+求点D的坐标．变式拓展(1)求点A，B，C的坐标．(2)若点P在直线1l上，且(3)根据图象，直接写出当【答案】(1)48, A⎛-(1)直接写出点A的坐标为。

一次函数的图象性质一次函数，又称为一次方程，是一个特殊的函数形式，由形如y =ax + b的方程所表示，其中a和b为常数，而x和y则为变量。

一次函数的图象性质在数学中具有重要的地位，对于理解线性关系、解决实际问题以及推导其他函数的性质都具有指导作用。

在本文中，将探讨一次函数的图象性质，并从图像的倾斜度、截距和交点着手进行分析。

一、图像的倾斜度一次函数的图象通常表现为一条直线，其倾斜度能够反映函数的性质。

对于y = ax + b这样的一次函数来说，a被称为斜率，用来描述图象的倾斜程度。

当a大于0时，图象向右上方倾斜；当a小于0时，图象向右下方倾斜；当a等于0时，图象为一条水平直线。

斜率的绝对值越大，图象的倾斜程度越大。

倾斜度的大小决定了一次函数在平面上的变化速度。

斜率的正负决定了函数是否单调增减，当斜率大于0时，函数单调增加；当斜率小于0时，函数单调减少；当斜率等于0时，函数保持水平。

当斜率为正或者负无穷大时，函数表现为垂直于x轴或y轴的直线。

二、截距一次函数的截距是指函数图象与坐标轴的交点位置。

根据函数的形式y = ax + b，我们可以得到两个重要的截距：x轴截距和y轴截距。

x轴截距，即函数与x轴的交点的横坐标，可以通过令y等于0解方程得到：0 = ax + b，解得x = -b/a。

同理，y轴截距可以通过令x等于0解方程得到：y = a*0 + b，解得y = b。

截距与函数在图像上的位置有密切的关系。

x轴截距决定了函数图像与x轴的交点位置，在平面上表现为函数图像与x轴的交点横坐标。

y轴截距则决定了函数图像与y轴的交点位置，在平面上表现为函数图像与y轴的交点纵坐标。

三、交点对于两条一次函数来说，它们可能有一个、两个或者不存在交点。

交点是两条函数图像相交处的坐标点，也是两个方程的解。

通过求解两个方程，我们可以确定交点的位置。

当两条函数图像有一个交点时，表示两个方程存在唯一解；当两条函数图像有两个交点时，表示两个方程存在两个解；当两条函数图像没有交点时，表示两个方程无解。

一次函数的图象和性质一、知识要点：1、一次函数：形如y=kx+b (k≠0, k, b为常数)的函数。

注意：（1）k≠0,否则自变量x的指数为1；（2）当b=0时，y=kx，y叫x的正比例函数。

2、图象：一次函数的图象是一条直线，（1）两个特殊点：y=kx+b 与y轴交于（0，b）；与x轴交于（-，0）y=kx （0，0）；（1，k）（2）由图象可以知道，直线y=kx+b与直线y=kx平行，它可以看作由直线 y=kx 平移｜b｜个单位长度而得到（当b>0时向上平移；当b<0时向下平移）例如直线：y=2x+3与直线y=2x-5都与直线y=2x平行。

3、性质：(1)图象的位置:k>0时直线y=kx经过一、三象限，从左向右上升Y随着x的增大而增大；k<0时直线y=kx经过二、四象限，从左向右下降Y随着x的增大而减小k>0 b>0时直线y=kx+b经过一、二、三象限，从左向右上升y随着x的增大而增大；k>0 b<0时直线y=kx+b经过一、三、四象限，从左向右上升y随着x的增大而增大k<0 b>0时直线y=kx+b经过一、二、四象限，从左向右下降y随着x的增大而减小k<0 b<0时直线y=kx+b经过二、三、四象限，从左向右下降y随着x的增大而减小4．求一次函数解析式的方法求函数解析式的方法主要有三种(1)由已知函数推导或推证(2)由实际问题列出二元方程，再转化为函数解析式，此类题一般在没有写出函数解析式前无法（或不易）判断两个变量之间具有什么样的函数关系。

(3)用待定系数法求函数解析式。

“待定系数法”先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法。

本单元构造方程一般有下列几种情况：①利用一次函数的定义构造方程组。

②利用一次函数y=kx+b中常数项b恰为函数图象与y轴交点的纵坐标，即由b来定点；直线y=kx+b平行于y=kx，即由k来定方向。

一次函数的性质和图像目录一、函数的定义（一）、一次函数的定义函数。

（二）、正比例函数的定义二、函数的性质（一）、一次函数的性质（二）、正比例函数的性质三、函数的图像（一）、一次函数和正比例函数图像在坐标上的位置（二）、一次函数的图像1、一次函数图像的形状2、一次函数图像的画法（三）、正比例函数的图像1、正比例函数图像的形状2、正比例函数图像的画法3、举例说明正比例函数图像的画法四、k、b两个字母对图像位置的影响K、b两个字母的具体分工是：（一次项系数）k决定图象的倾斜度。

（常数项）b决定图象与y轴交点位置。

五、解析式的确定（一）一个点坐标决定正比，两个点坐标决定一次（二）用待定系数法确定解析式六、两条函数直线的四种位置关系两直线平行，k1= k2，b1≠b2两直线重合，k1= k2，b1=b2两直线相交，k1≠k2两直线垂直，k1×k2=－1（一）两条函数直线的平行（二）两条函数直线的相交（三）两条函数直线的垂直一次函数、反比例函数中自变量x前面的字母k称为比例系数这一节我们要学习正比例函数和一次函数。

一次函数的解析式是y=kx+b，如果当这个式子中的b=0时，式子就变成了正比例函数y=kx。

因此，正比例函数是一次函数当b=0时的特殊情况。

正是因为正比例函数实际上就是一次函数，所以把正比例函数和一次函数结合在一起来学习。

在正比例函数y=kx和反比例函数y=k/x中，由于函数y与自变量x之间有比例关系，就要在自变量x前面用字母系数k表示它们之间的比例关系，因而字母k就取名为比例系数。

确定了比例系数k就可以直接确定正比例函数或反比例函数的解析式。

但是，在一次函数y=kx+b和二次函数y=ax2+bx+c中，我们从观察解析式就可以看出，函数y与自变量x之间没有相直接对应的比例关系，因此这两种函数自变量x前面的k，就不能叫比例系数，只能叫常数。

若欲确定一次函数或二次函数的解析式时，题意仅已知常数k还不行，还需要其他常数如b、c等常数的协助。

一次函数图像及其性质一、一次函数图像1、一次函数y=kx+b 的k 、b 的值对一次函数图象的影响：① ② ③ ④①k ﹥0,b ﹥0, y ＝kx +b 的图象在一、二、三象限；②k ﹥0, b ﹤0, y ＝kx +b 的图象在一、三、四象限； ③k ﹤0,b ﹥0, y ＝kx +b 的图象在一、二、四象限；④k ﹤0, b ﹤0, y ＝kx +b 的图象在二、三、四象限。

2、一次函数的性质⑴正比例函数y=kx(k≠0)是特殊的一次函数，当k>0时，图象过一、三象限，y 随x 的增大而_增大__； 当k<0时，图象过__二、四__象限；y 随x 的增大而_减小___.⑵一次函数y=kx ＋b(k ≠ 0)的图象平行于直线y = kx ,可由它平移而得，当k>0时，y 随x 的增大而_增大_； 当k<0时，y 随x 的增大而__减小_k>0时，k 越大，y 增长得越快；k<0时，k 越大，减小得越快；⑴在一次函数y=kx ＋b 中，令y=0，得一元一次方程kx ＋b=0，它的根就是一次函数y=kx ＋b 的图象与x 轴交点的横坐标.⑵一元一次不等式kx ＋b>0(或kx ＋b<0)的解集可以看作一次函数y=kx ＋b 当函数值大于或小于0时相应的自变量x 值的取值范围.⑶两直线交点的坐标，就是由这两条直线的解析式组成的二元一次方程组的解.题型考点一：一次函数的增减性例1、已知关于x 的一次函数2(3)2y m x m =-++-．(1) m 为何值时，函数的图象和直线y=－x 平行? (2)m 为何值时，y 随x 的增大而减小？【变式】已知一次函数y=（3-k ）x-2k 2+18. （1）k 为何值时，它的图象经过原点？ （2）k 为何值时，它的图象经过点（0，-2）?（3）k 为何值时，它的图象与y 轴的交点在x 轴的上方？ （4）k 为何值时，它的图象平行于直线y=x ？ （5）k 为何值时，y 随x 的增大而减小？题型考点二：一次函数图像与象限关系例2、直线y=x+b （b>0）与直线y=kx （k<0）的交点位于（）A 、第一象限B 、第二象限C 、第三象限D 、第四象限【练习】若实数a ，b 满足ab ＜0，且a ＜b ，则函数y=ax+b 的图象可能是（ ）题型考点三：一次函数图像的交点例3、如图，在平面直角坐标系中，线段AB 的坐标为A （-2,4），B （4,2），直线y=kx-2与线段AB 有交点，则k 的值不可能是（） A 、-5 B 、-2 C 、3 D 、5【练习】如图，直线l ：233y x =--与直线y a =（a 为常数）的交点在第四象限， 则a 可能在（）A 、1<a<2B 、-2<a<0C 、32a -≤≤-D 、-10<a<-4二、一次函数与一元一次方程的关系直线y b k 0kx =+≠（）与x 轴交点的横坐标，就是一元一次方程b 0(0)kx k +=≠的解。