正方形的性质和判定定理
- 格式:doc
- 大小:32.00 KB
- 文档页数:2

正方形的性质和判定定理
根据以上的关系图,得到正方形、矩形和菱形三者的关系:正方形既是矩形也是菱形。
同时利用维恩图表示:
(1)选择题(正方形的性质)1、正方形具有而矩形不一定具有
师:从问题出发,求角的度数有什么思路?此处用到正方形何性质?
)证明题(正方形判定和
第一问在教师引导下解决完,提出以下问题:
本课主要学习了正方形的定义、性质、判定方法,正方形既是特殊的平行四边形,也是特殊的矩形,还
1、必做题
如图,四边形ABCD中,AD//BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形.
(2)如果BE=BC 且
、选做题。



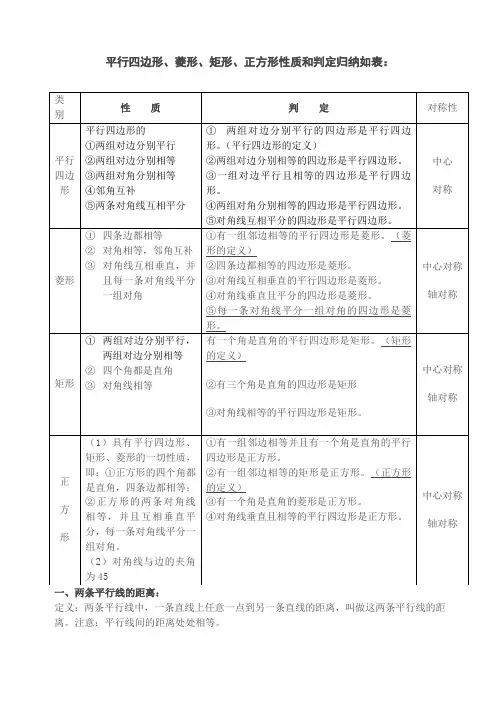
平行四边形、菱形、矩形、正方形性质和判定归纳如表:
定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线的距离。
注意:平行线间的距离处处相等。
二、矩形的一条对角线把矩形分成两个直角三角形,与之相联系的还有以下性质:(1)直角三角形的两个锐角互余。
(2)直角三角形两直角边的平方和等于斜边的平方。
(即勾股定理)
(3)直角三角形斜边上的中线等于斜边的一半。
(4)直角三角形中30 角所对的直角边等于斜边的一半。
四种特殊四边形的性质
四种特殊四边形常用的判定方法:
一组邻
一组邻
边相等对角线相
对角线
垂直
对角线
相等
对角线垂
直。



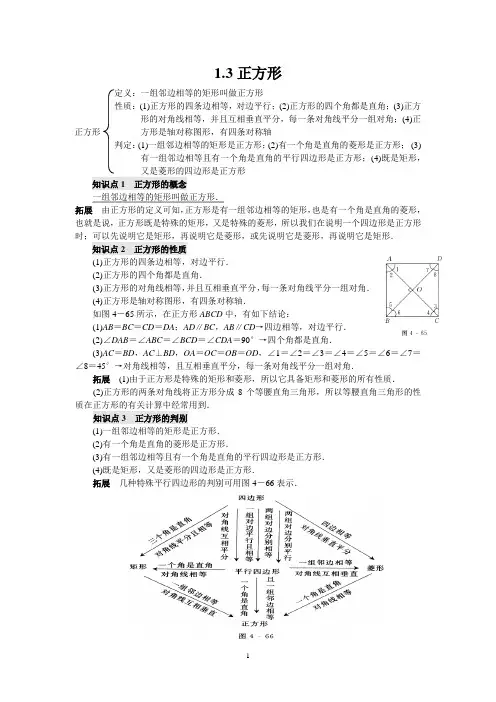
1.3正方形定义:一组邻边相等的矩形叫做正方形性质:(1)正方形的四条边相等,对边平行;(2)正方形的四个角都是直角;(3)正方形的对角线相等,并且互相垂直平分,每一条对角线平分一组对角;(4)正方形是轴对称图形,有四条对称轴判定:(1)一组邻边相等的矩形是正方形;(2)有一个角是直角的菱形是正方形;(3)有一组邻边相等且有一个角是直角的平行四边形是正方形;(4)既是矩形,又是菱形的四边形是正方形知识点1 正方形的概念一组邻边相等的矩形叫做正方形.拓展由正方形的定义可知,正方形是有一组邻边相等的矩形,也是有一个角是直角的菱形,也就是说,正方形既是特殊的矩形,又是特殊的菱形,所以我们在说明一个四边形是正方形时;可以先说明它是矩形,再说明它是菱形,或先说明它是菱形,再说明它是矩形.知识点2 正方形的性质(1)正方形的四条边相等,对边平行.(2)正方形的四个角都是直角.(3)正方形的对角线相等,并且互相垂直平分,每一条对角线平分一组对角.(4)正方形是轴对称图形,有四条对称轴.如图4-65所示,在正方形ABCD中,有如下结论:(1)AB=BC=CD=DA;AD∥BC,AB∥CD→四边相等,对边平行.(2)∠DAB=∠ABC=∠BCD=∠CDA=90°→四个角都是直角.(3)AC=BD,AC⊥BD,OA=OC=OB=OD,∠1=∠2=∠3=∠4=∠5=∠6=∠7=∠8=45°→对角线相等,且互相垂直平分,每一条对角线平分一组对角.拓展(1)由于正方形是特殊的矩形和菱形,所以它具备矩形和菱形的所有性质.(2)正方形的两条对角线将正方形分成8个等腰直角三角形,所以等腰直角三角形的性质在正方形的有关计算中经常用到.知识点3 正方形的判别(1)一组邻边相等的矩形是正方形.(2)有一个角是直角的菱形是正方形.(3)有一组邻边相等且有一个角是直角的平行四边形是正方形.(4)既是矩形,又是菱形的四边形是正方形.拓展几种特殊平行四边形的判别可用图4-66表示.正方形规律方法小结从一般到特殊的思想:从四边形到平行四边形再到菱形、矩形,再到正方形,就是从一般情况到特殊情况的认识,体现了从一般到特殊的思想.四边形、平行四边形、矩形、菱形、正方形之间的关系如图4—67所示.1、如图4-70所示,在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连接AE交CD于F,则∠E=.2、如图4-72所示,△ABC中,∠ACB=90°,CD平分∠ACB,交AB于0,DE⊥AC,D F⊥BC,E,F是垂足,那么四边形DECF是正方形吗?说明理由.3、如图4-74所示,四边形ABCD是正方形,E,F是AD,DC上的点,且∠EBF=45°,则EF与CF+AE相等吗?说明理由.4、如图4-76所示,将矩形ABCD中的△AOB沿着射线BC的方向平移线段AD的距离,(1)画出△AOB平移后的图形;(2)设(1)中O点平移后的对应点为E,试判断四边形CODE的形状,并说明理由;(3)当四边形ABCD是什么四边形时,(2)中的四边形C00E是正方形?并说明你的理由.体验中考 1、如图4-80所示,将边长为8 cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的长是 ( )A .3 cmB .4 cmC .5 cmD .6 cm2、如图4-8l(1)所示,把一个长为m ,宽为n 的长方形(m >n )沿虚线剪开,拼接成图(2),成为在一个角去掉—个小正方形后的一个大正方形,则去掉的小正方形的边长为 ( )A .2m nB .m -nC .2m D .2n 3、如图4-82所示,正方形ABCD 内有两条相交线段MN ,EF ,M ,N ,E ,F 分别在边AB ,CD ,AD ,BC 上,小明认为:若MN =EF ,则MN ⊥EF ;小亮认为:若MN ⊥EF ,则MN =EF .你认为 ( )A. 仅小明对 B .仅小亮对 C .两人都对 D .两人都不对作业1.顺次连接菱形各边中点所得的四边形一定是( ) A.等腰梯形 B.正方形 C.平行四边形 D.矩形 2. 在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的是( ) A 、AC=BD ,∠A=∠B ,∠C=∠D B 、∠ABD=∠CBD ,AB=CD ,∠A=∠B C 、AO=CO ,BO=DO ,∠A=∠B D 、AO=CO=BO=DO ,AB=BC3.如图1,已知正方形ABCD 的边长为,E 为DC 边上一点,∠EBC=30°,则BE 的长为( )A 、cm 5B 、cm 52C 、5cmD 、10cm4.如图4-4-2,等边三角形ABE 与正方形ABCD 有一条公共边,则∠AED 等于( ) A 、10°B 、12.5°C 、15°D 、20°5.如图4-4-3,E 是正方形ABCD 内一点,且△EAB 是等边三角形,则∠ADE 等于cm 35图1图3BA DCB O( )A 、70° B 、72.5° C 、75° D 、77.5°6.如图所示,菱形中,对角线相交于点,若再补充一个条件能使菱形成为正方形,则这个条件是 (只填一个条件即可)7. 如图(1),在正方形ABCD 的边BC 的延长线上取一点E ,使CE =AC ,连结AE 交CD 于F ,则∠AFC =(1) (2)8.如图(2),E 是正方形ABCD 内一点,如果△ABE 是等边三角形,那么∠DCE =,如果DE 的延长线交BC 于G ,则∠BEG =9.已知:如图,正方形ABCD 中,延长AD 到E ,使DE=AD ,再延长DE 到F ,使DF=BD ,连接BF ,交CE 于M ,交DC 于N.求证:MD=MN.10.如图,△ABC 中,点O 是AC 上一动点,过点O 作直线MN ∥BC ,设Mn 交∠ACB 的平分线于点E ,交∠ACH 的平分线于点F 。
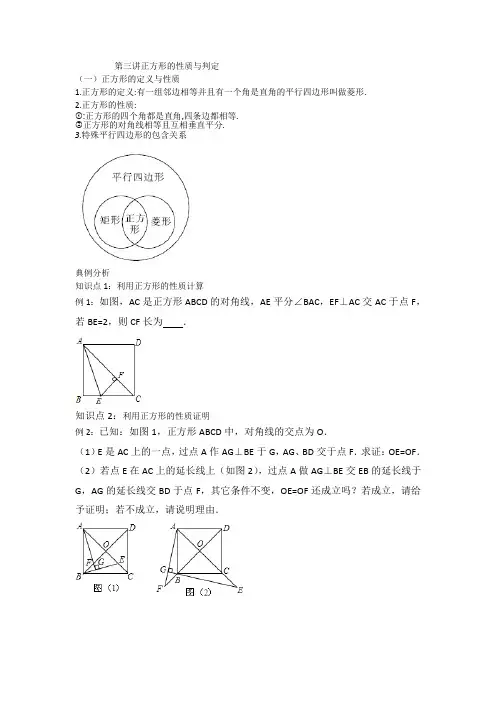
第三讲正方形的性质与判定(一)正方形的定义与性质1.正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做菱形.2.正方形的性质:①:正方形的四个角都是直角,四条边都相等.②正方形的对角线相等且互相垂直平分.3.特殊平行四边形的包含关系典例分析知识点1:利用正方形的性质计算例1:如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为.知识点2:利用正方形的性质证明例2:已知:如图1,正方形ABCD中,对角线的交点为O.(1)E是AC上的一点,过点A作AG⊥BE于G,AG、BD交于点F.求证:OE=OF.(2)若点E在AC上的延长线上(如图2),过点A做AG⊥BE交EB的延长线于G,AG的延长线交BD于点F,其它条件不变,OE=OF还成立吗?若成立,请给予证明;若不成立,请说明理由.知识点3:利用正方形的性质求面积例3:(1)如图,正方形ABCD的边长为2,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是.例3(1)图例3(2)图(2)如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG 的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为()A.a2B.a2 C.a2D.a2知识点4:利用正方形解决最短路径问题例4:如图,正方形ABCD的边长为6,E为BC上的一点,BE=2,F为AB上的一点,AF=3,P为AC上一点,则PF+PE的最小值为.(二)正方形的判定1.正方形的判定定理.(1)有一组邻边相等的矩形是正方形.(2)有一个角是直角的菱形是正方形.(3)对角线垂直的矩形是正方形.(4)对角线相等的菱形是正方形.2..判定一个四边形是矩形的方法与思路是:典例分析知识点5:先证矩形再证正方形例5.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.知识点6:先证菱形再证正方形例6:如图,已知在▱ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.(1)求证:四边形ABCD是菱形;(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.(三)中点四边形1.定义:以四边形的各边中点为顶点所组成的新四边形2.决定中点四边形EFGH的形状的主要因素是原四边形ABCD的对角线的长度和位置关系.(1)若原四边形的对角线相等,则中点四边形EFGH为菱形;(2)若原四边形的对角线互相垂直,则中点四边形EFGH为矩形;(3)若原四边形的对角线既相等又垂直,则中点四边形EFGH为正方形;(4)若原四边形的对角线既不相等也不垂直,则中点四边形EFGH为平行四边形知识点7:中点四边形形状的确定例7:(1)以四边形的各边中点为顶点可以组成一个什么图形?如果以菱形或矩形各边的中点为顶点呢?:(2)如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别为AB、BC、CD、DA的中点.(1)求证:四边形EFGH为正方形;(2)若AD=1,BC=3,求正方形EFGH的边长.(四)正方形的性质与判定的综合应用例8:如图,正方形ABCD边长为6.菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,且AH=2,连接CF.(1)当DG=2时,求证:菱形EFGH为正方形;(2)设DG=x,试用含x的代数式表示△FCG的面积.例9:如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?例10:如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=BC=1.(1)求证:CE=CF;(2)若G在AD上,连接GC,且∠GCE=45°,求∠GCF的度数;(3)在(2)的条件下,求GC的长度.例11:如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.(1)求证:AD=AF;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.例12:(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC 延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.(下面请你完成余下的证明过程)(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=时,结论AM=MN仍然成立.(直接写出答案,不需要证明)夯实基础:1.下列说法中,正确的是()A.有一个角是直角的四边形是菱形B.对角线互相垂直的菱形是正方形C.对角线相等的平行四边形是矩形D.一组邻边相等的平行四边形是正方形2.已知正方形的边长为2cm,则其对角线长是()A.4cm B.8cm C.cm D.2cm3.如图,直线l过正方形ABCD的顶点B,点A、C至直线l的距离分别为2和3,则此正方形的面积为()A.5 B.6 C.9 D.13第3题第4题第5题4.如图,在正方形ABCD中,AB=1,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为()A.B.4 C.2 D.5.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是()A.3 B.4 C.5 D.66.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°第6题第7题7.如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为()A.﹣4+4B.4+4 C.8﹣4D.+18.如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为()A.2B.3C.D.第8题第9题9.如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2=.10.已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF ∥BE.求证:四边形BECF是正方形.11.如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF ⊥AC,垂足分别为E,F.(1)求证:△BED≌△CFD;(2)当∠A=90°时,试判断四边形DFAE是何特殊四边形?并说明理由.13..如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且交边CD于点E.(1)求证:PB=PE;(2)过点E作EF⊥AC于点F,如图2,若正方形ABCD的边长为2,则在点P 运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.14.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)。
青岛版数学八年级下册《正方形的性质和判定定理》教学设计一. 教材分析《正方形的性质和判定定理》是青岛版数学八年级下册的教学内容。
本节课的主要内容是让学生了解正方形的性质和判定定理,掌握正方形的特点和判定方法,为后续学习正多边形和圆的知识打下基础。
教材通过丰富的图片和实例,引导学生探究正方形的性质,并通过推理和证明,使学生掌握正方形的判定定理。
二. 学情分析学生在七年级时已经学习了矩形、菱形等四边形的性质,对平行四边形的性质有一定的了解。
但正方形与这些四边形有所不同,它的特殊性质和判定定理需要学生通过探究和证明来掌握。
因此,在教学过程中,教师需要关注学生的学习兴趣,激发学生的探究欲望,引导学生通过自主学习和合作交流,理解和掌握正方形的性质和判定定理。
三. 教学目标1.了解正方形的性质,并能运用这些性质解决相关问题。
2.掌握正方形的判定定理,并能运用判定定理判断一个四边形是否为正方形。
3.培养学生的观察能力、推理能力和证明能力。
4.激发学生对数学的兴趣,培养学生的合作意识和创新精神。
四. 教学重难点1.正方形的性质和判定定理的理解和运用。
2.正方形性质和判定定理的证明过程。
五. 教学方法1.引导探究法:教师引导学生通过观察、操作、推理和证明,自主探究正方形的性质和判定定理。
2.合作交流法:学生分组进行探究,分享学习成果,互相学习和交流。
3.案例分析法:教师通过展示正方形的实际应用案例,引导学生理解和运用正方形的性质和判定定理。
六. 教学准备1.教学PPT:包含正方形的性质和判定定理的相关内容,以及实际应用案例。
2.教学素材:正方形的图片、实物模型等。
3.练习题:用于巩固学生对正方形性质和判定定理的理解和运用。
七. 教学过程1.导入(5分钟)教师通过展示一些正方形的实际应用案例,如正方形地毯、正方形桌面等,引导学生关注正方形的特点,激发学生的学习兴趣。
2.呈现(10分钟)教师通过PPT呈现正方形的性质和判定定理,引导学生观察和思考,引导学生用自己的语言描述正方形的特点。
正方形的判定和性质探索活动1、思考:你能类比矩形、菱形的概念给正方形下个定义吗?正方形的概念:____________并且____________的_________是正方形。
2、探究:(1)比较平行四边形、矩形、菱形、正方形之间的关系(2)探索正方形的性质请大家思考正方形有哪些性质?正方形是一个特殊的平行四边形,正方形形具有平行四边形的所有性质;正方形还是特殊的矩形,也是特殊的菱形,所以正方形具有矩形、菱形的所有性质正方形的性质:从对称性看:正方形既是轴对称图形,又是中心对称图形从边看:正方形的四边相等,对边平行从角看:正方形4个角都是直角从对角线看:正方形的两条对角线相等且互相垂直平分;每一条对角线平分一组对角思考:正方形具有而一般矩形不具备的性质:正方形具有而一般菱形不具备的性质:探索正方形的判定方法:问题:有一个角是直角的是正方形;有一组邻边相等的是正方形;对角线相等的是正方形;对角线垂直的是正方形;对角线的四边形是正方形。
思路:(1)先说明这个平行四边形是,再说明这个矩形也是;(2)先说明这个平行四边形是,再说明这个菱形也是。
归纳总结例1.如图,四边形ABCD 和四边形CEFG 都是正方形,试探索BG 与DE 的关系.例2.在正方形ABCD 中,点E、F、G、H 分别在各边上,且AE=BF=CG=DH.四边形EFGH 是正方形吗?为什么?题型一:正方形的性质-求角度1.如图,正方形ABCD O,则AOB ∠的度数是()A.30︒B.45︒C.60︒D.90︒【答案】D 【详解】解:∵四边形ABCD 是正方形,∴AC BD ⊥,∴90AOB ∠=︒,故选:D.2.如图,在正方形ABCD 中,E 为AD 上一点,连接BE ,BE 交对角线AC 于点F,连接DF ,若35ABE ∠=︒,则CFD ∠的度数为()A.80°B.70°C.75°D.45°【答案】A 【详解】解:∵四边形ABCD 是正方形,∴,45BC CD BAC ACB ACD =∠=∠=∠=︒,∵35ABE ∠=︒,∴80BFC ABE BAC ∠=∠+∠=︒,在BCF △和DCF 中,BC CD ACB ACD CF CF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BCF DCF ≌△△,∴80CFD CFB ∠=∠=︒,故选:A.3.如图,在正方形ABCD 的外侧,作等边ADE V ,则AEB ∠=.【答案】15︒【详解】解:∵四边形ABCD 是正方形,∴AB AD =,90BAD ∠=︒,∵ADE 是等边三角形,,∴AD AE =,60DAE ∠=︒,∴AB AE =,150BAE ∠=︒,∴()1180150152AEB ∠=︒-︒=︒,故答案为:15︒.4.如图,正方形ABCD 中,E 在BC 延长线上,AE,BD 交于点F,连接FC,若32E ∠= ,那么BCF ∠的度数是.【答案】58°【详解】解:∵在正方形ABCD,AD=CD,∠ADF=∠CDF=45°,DF=DF,∴△ADF≌△CDF(SAS),∴∠DAF=∠DCF,又∵AD∥BC,∠E=32°,∴∠DAF=32°,∴∠DCF=32°,∴∠BCF=∠DCB-∠DCF=90°-32°=58°.故答案为:58°.5.如图,在正方形ABCD 中,M 是正方形内一点,且MC MD AD ==.求BAM ∠的度数.【答案】15︒【详解】解:在正方形ABCD 中,90ADC BAD ∠=∠=︒,AD DC =,MC MD AD ==,AD DC MD MC ∴===,在DMC 中,DM DC MC ==,则DMC 是等边三角形,60MDC ∴∠=︒,30MDA ∴∠=︒,在ADM △中,30ADM ∠=︒,MD AD =,则()118030752DAM ∠=︒-︒=︒;90907515BAM DAM ∴∠=︒-∠=︒-︒=︒.6.如图,BF 平行于正方形ADCD 的对角线AC,点E 在BF 上,且AE=AC,CF∥AE,求∠BCF.【答案】105°【详解】作AO⊥FB 的延长线,BQ⊥AC∵BF∥AC,∴AO∥BQ 且∠QAB=∠QBA=45°∴AO=BQ=AQ=12AC ∵AE=AC ∴AO=12AE∴∠AEO=30°∵BF∥AC∴∠CAE∠AEO=30°∵BF∥AC,CF∥AE∴∠CFE∠CAE=30°∵BF∥AC∴∠CBF∠BCA=45°∠BCF=180°-∠CBF-∠CFE=180°-45°-30°=105°题型二:正方形的性质-求长度1.正方形的一条对角线长为8,则正方形的边长为()A.2B.4C.D.【答案】C【详解】解:设正方形的边长为a,∵正方形的一条对角线之长为8,a a+=,∴2228∴a=,故选C.2.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和3,则正方形的边长是..【详解】试题分析:∵四边形ABCD是正方形,∴AB=CD,∠ABM+∠CBN=90°.∵AM⊥MN,CN⊥BN,∴∠BAM=∠CBN,∠AMB=∠CNB=90°.∴△AMB≌△BCN(AAS).∴BM=CN.∵点A、C到直线L的距离分别是1和3,即AM=1,CN=3,∴BM=3.∴AB ==3.如图,在边长为ABCD 中,30∠=︒CDE ,DE CF ⊥则AF 的长为()A.4-B.4C.4-D.4-【答案】D 【详解】解∶∵四边形ABCD 是正方形,∴90FBC DCE CD BC ∠=∠=︒==,Rt DCE V 中,30∠=︒CDE ,∴12CE DE =,设CE x =,则2DE x =,根据勾股定理得∶222DC CE DE +=,即(()2222x x +=,解得∶4x =±(负值舍去),∴4CE =,∵DE CF ⊥,∴90DOC ∠=︒,∴60DCO ∠=︒,∴906030BCF CDE ∠=︒-︒=︒=∠,∵DCE CBF CD BC ∠=∠=,,∴()ASA DCE CBF ≌,∴4BF CE ==,∴4AF AB BF =-=-.故选∶D.4.如图,边长为6的正方形ABCD 中,M 为对角线BD 上的一点,连接AM 并延长交CD 于点P.若PM PC =,则AM 的长为()A.)31B.)32C.)61D.)62【答案】C【详解】∵边长为6的正方形ABCD ,∴,,90BA BC ABM CBM DAB ADC BCD =∠=∠∠=∠=∠=︒,∵BA BC ABM CBM BM BM =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABM CBM ≌,∴BAM BCM ∠=∠,∴9090BAM BCM ︒-∠=︒-∠,∴DAM DCM ∠=∠,∵PM PC =,∴PMC DCM ∠=∠,∴22APD PMC DCM DCM DAM ∠=∠+∠=∠=∠,∴390APD DAM DAM ∠+=∠=︒,∴30DAP ∠=︒,∴2AP DP =,∵222AP DP AD =+∴()22226DP DP =+,解得DP =∴262AP DP PM PC CD DP ====-=-∴)661AM AP PM =-==,故选C.5.如图,在正方形ABCD 中,将边BC 绕点B 逆时针旋转至BC ',连接CC ',DC ',若90CC D '∠=︒,5AB =,则线段C D '的长度为.【详解】解:过点B 作BE CC '⊥于点E ,四边形ABCD 是正方形,BC CD ∴=,90BCD ∠=︒,90BCE C CD '∴∠+∠=︒,90BCE CBE ∠+∠=︒ ,C CD CBE '∴∠=∠,又BEC CC D '∠=∠ ,在BCE 和'CDC △中,CBE C CD BEC CC D BC CD ∠=∠⎧⎪∠=∠='⎨'⎪⎩,()AAS BCE CDC '∴≌ ,CE C D '∴=,将边BC 绕点B 逆时针旋转至BC ',5BC BC CD '∴===,又BE CC '⊥ ,CE C E C D ''∴==,222C D C C CD ''+= ,2525C D '∴=,C D '∴=,6.如图,正方形ABCD 的对角线交于点O ,点E 是线段OD 上一点,连接EC ,若BF CE ⊥于点F ,BF 是DBC ∠的角平分线,6AB =,则OE 的长为.【答案】6-【详解】解: 四边形ABCD 是正方形,6BC AB ∴==,90ABC ∠=︒,在Rt ABC △中,AC === 正方形ABCD 的对角线AC ,BD 交于点O,1122BO BD AC ∴===BF CE ⊥ 于点F ,90BFE BFC ∴∠=∠=︒,BF 是DBC ∠的角平分线,EBF CBF ∴∠=∠,在BFE △和BFC △中,90EBF CBF BF BF BFE BFC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴(ASA)BFE BFC ≌ ,6BE BC ∴==,6OE BE BO ∴=-=-故答案为:6-.题型三:正方形的性质-求周长和面积1.正方形一条对角线为2,则正方形的面积为.【答案】2【详解】解: 正方形的一条对角线的长为2,∴这个正方形的面积21222=⨯=.故答案为:2.2.如图,边长为2的正方形ABCD 的对角线相交于点O,过点O 的直线分别交AD 、BC 于E、F,则阴影部分的面积是.【答案】1【详解】解:在正方形ABCD 中,AD BC ∥,OD OB =,∴ODE OBF ∠=∠,又DOE BOF ∠=∠,∴()ASA DEO BFO ≌△△,DEO BFO S S ∴=△△,阴影面积=BOC S 12112=⨯⨯=.故答案为:1.3.如图,正方形ABCD 中,AB=1,点P 是对角线AC 上的一点,分别以AP、PC 为对角线作正方形,则两个小正方形的周长的和是.【答案】4cm.【详解】解:设小正方形的边长为x,则较大的正方形的边长为1-x,故两个小正方形的周长和=4x+4(1-x)=4cm.4.如图,正方形ABCD 和正方形EFGO 的边长都是2,正方形EFGO 绕点O 旋转时,两个正方形重叠部分的面积是()A.1B.2C.3D.4【答案】A 【详解】解:如图,设AB 与OE 交点N,BC 与OG 交点M,∵四边形ABCD 和四边形EFGO 都是正方形,∴,45,90OB OC OBA OCB BOC EOG =∠=∠=︒∠=∠=︒,∴BON MOC ∠=∠.在OBN △与OCM 中,OBN OCM OB OC BON COM ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ASA OBN OCM ∴≌ ,OBN OCM S S ∴= ,1122144OBC ABCD OMBN S S S ∴===⨯⨯=正方形四边形 .故选:A.5.正方形ABCD 的边长为2,将该正方形绕顶点A 在平面内旋转45︒,则旋转后的图形与原图形重叠部分的面积为()A.4B.4-C.10-D.8-【答案】A 【详解】解:设C D ''交BC 于点M ,连AM ,四边形ABCD 是边长为2的正方形,2AD AB ∴==,90D B BAD ∠=∠=∠=︒,由旋转得AD AD '=,D D '∠=∠,45DAD '∠=︒,AD AB '∴=,90D B '∠=∠=︒,45BAD BAD DAD ''∠=∠-∠=︒,在Rt AD M '△和Rt ABM 中,AM AM AD AB=⎧⎨'=⎩,∴Rt Rt (HL)AD M ABM '△≌△,122.52MAD MAB BAD ''∴∠=∠=∠=︒,在AB 上截取BE BM =,连接EM ,则45BEM BME ∠=∠=︒,22.5EMA BEM MAB ∴∠=∠-∠=︒,EMA MAB ∴∠=∠,AE ME ∴=,∴2BE +=,2BM BE ∴==,1122)222AD M ABM S S AB BM '∴==⋅=⨯⨯=-△△,224AD M ABM S S S '∴=+=-+-=-△△阴影,故选:A.6.如图,已知正方形,ABCD G 为CD 边上一点(不与端点重合),以CG 为一边作正方形CGFE ,连接,,BD BF DF ,若4AB =,则BDF V 的面积为.【答案】8【详解】解:连接CF ,∵四边形ABCD 和四边形CGFE 是正方形,∴45DBC FCE ∠=∠=︒,∴BD CF ∥,∴1144822BDF BDC ABCD S S S ===⨯⨯= 正方形,故答案为:8.7.如图,边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为1S 、2S ,则12S S +的值为.【答案】68【详解】解:如图所示,连接BQ FH EG ,,,过点F 作FR AD ⊥于点R ,过点G 作GK CD ⊥于点K ,∵四边形ABCD ,四边形EFGH ,四边形BPQS 是正方形,AC 是对角线,BQ 是对角线,∴90SQP CSQ QPA ∠=∠=∠=︒,45BCA BAC CQS PQA SQB PQB SBQ PBQ ∠=∠=∠=∠=∠=∠=∠=∠=︒,∴,,,APQ QPB BQS CSQ △△△△是等腰直角三角形,且APQ QPB BQS CSQ ≌≌≌△△△△,同理,,,,,,,,,ARF ERF EOF EOH EDH HOG HKG GKC GOF △△△△△△△△△是等腰直角三角形,且ARF ERF EOF EOH EDH HOG HKG GKC GOF ≌≌≌≌≌≌≌≌△△△△△△△△△,∴149ADC S S =△,212ABC S S =△,12ADC ABC ABCD S S S +=正方形△△,∴124111121212123236689222S S +=⨯⨯⨯+⨯⨯⨯=+=,故答案为:68.题型四:正方形的性质运用1.菱形、矩形、正方形都具有的特点是()A.对角线互相垂直B.对角线相等C.对角线互相平分D.对角线平分对角【答案】C【详解】解:A.矩形的对角线不一定互相垂直,故不符合题意;B.菱形的对角线不一定相等,故不符合题意;C.菱形、矩形、正方形的对角线互相平分,故符合题意;D.矩形的对角线不一定平分对角,故不符合题意;故选:C.2.下列性质中,平行四边形,矩形,菱形,正方形共有的性质是()A.对角线相等B.对角线互相垂直C.对角线互相平分D.对角线平分内角【答案】C【详解】解:∵平行四边形的对角线互相平分,∴矩形,菱形,正方形的对角线也必然互相平分.故选:C.3.在学习了“中心对称图形——平行四边形”之后,平行四边形、矩形、菱形、正方形的关系可以用下面的关系图表示,则②处所填图形的名称应为.【答案】正方形【详解】解:由题意可知,④是平行四边形,①和③分别是矩形和菱形,②是正方形.故答案为:正方形.4.如图,以ABC 的边AB 、AC 为边分别向外作正方形ADEB 、ACGF ,连接DC 、BF 相交于M ,DC 、AB 相交于N .(1)从旋转的角度看,ADC △是绕点逆时针旋转度,可以得到ABF △;(2)CD 与BF 有何关系,请说明理由.【答案】(1)A ,90(2)CD BF =,DC BF ⊥,理由见解析【详解】(1)解:由题意知,从旋转的角度看,ADC △是绕点A 逆时针旋转90度,可以得到ABF △;故答案为:A ,90;(2)解:CD BF =,CD BF ⊥,理由如下:∵四边形ADEB 、四边形ACGF 均为正方形,∴90AD AB AC AF DAB CAF ==∠=︒=∠,,,∴DAB BAC CAF BAC ∠+∠=∠+∠,即DAC BAF ∠=∠,∵AD AB DAC BAF AC AF =∠=∠=,,,∴()SAS DAC BAF ≌,∴CD BF =,CDA FBA ∠=∠,∵180CDA DAN DNA FBA BMN BNM ∠+∠+∠=︒=∠+∠+∠,DNA BNM ∠=∠,∴90BMN DAN ∠=∠=︒,∴DC BF ⊥.题型五:最值问题1.如图,四边形ABCD 为正方形,M ,N 分别是AB ,BC 边的中点,请在对角线AC 上找一点P ,使PM PN +的值最小(不写作法,保留作图痕迹).【答案】见解析【详解】解:如图所示,点P 即为所求.连接BD 交AC 于O,连接NP 并延长交AD 于T,由正方形的对称性可知M T 、关于AC 对称,∴PM PT =,∴PM PN PT PN +=+,∴当P T M 、、三点共线时,PT PN +最小,即PM PN +最小,此时点P 与点O 重合.2.如图所示,正方形ABCD 的面积为9,ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P,使PD PE +的和最小,则这个最小值为()A.4.5B.9C.2.5D.3【答案】D 【详解】解:设BE 与AC 交于点P',连接BD ,DP ',∵点B 与D 关于AC 对称,∴''P D P B =,∴''''P D P E P B P E BE +=+=∵正方形ABCD 的面积为9,∴3AB =,又∵ABE 是等边三角形,∴3BE AB ==.故选:D3.正方形ABCD 中,点E 在AB 上,3AE =,1BE =,点P 在AC 上,EP BP +的最小值.【答案】5【详解】如图,连接BD 交AC 于点O ,连接ED 与AC 交于点P,连接PB ,∵四边形ABCD 是正方形,∴BD AC ⊥,且OB OD =,∴BP PD =,则BP EP ED +=,此时最短,∵3AE =,134AD =+=,∴根据勾股定理得22222234255ED AE AD =+=+==,∴5ED BP EP =+=,即BP EP +的最小值为:5,故答案为:5.4.如图,正方形ABCD 的边长为2,E 是CD 的中点,在对角线AC 上有一点P,则PD PE +的最小值是.【详解】连接BP ,BE ,因为正方形ABCD 关于对角线AC 对称,点B 与点D 是对称点,∴PB PD =,PD PE PB PE+=+当点P 在线段BE 上时,PD PE PB PE BE +=+=,为最小值.∵正方形ABCD 的边长为2,∴2BC CD ==,∵点E 是CD 的中点,∴112CE CD ==,∵在正方形ABCD 中,90BCD ∠=︒,∴在Rt BCE 中,BE ==∴PD PE +5.如图,在正方形ABCD 中,点E AB 上一点,且2AE =,4BE =,点P 是边AD 上的动点(P 与A ,D 不重合),则PE PC +的最小值是.【答案】10【详解】解:作点E 关于AD 的对称点E ',连接CE '交AD 于点P ,∴PE PE '=,AE AE '=,∴PE PC PE PC CE ''+=+≥,即PE PC +的最小值为CE ',∵四边形ABCD 是正方形,∴AB BC =,90CBA ∠=︒,∵2AE =,4BE =,∴4228BE BE AE AE ''=++=++=,642B E C AB BE A +=+===,在Rt BCE '△中,10CE '===,∴PE PC +的最小值是10.故答案为:10.题型六:正方形的判定定理1.如图,四边形ABCD 的对角线AC ,BD 交于点O,且OA OC =,OB OD =,下列说法错误的是()A.若AC BD ⊥,则ABCD 是菱形B.若AC BD =,则ABCD 是矩形C.若AC BD ⊥且AC BD =,则ABCD 是正方形D.若90ABC ∠=︒,则ABCD 是正方形【答案】D【详解】解:∵OA OC =,OB OD =,∴四边形ABCD 是平行四边形,若AC BD ⊥,则四边形ABCD 是菱形,故A 选项不符合题意;若AC BD =,则四边形ABCD 是矩形,故B 选项不符合题意;若AC BD ⊥且AC BD =,则四边形ABCD 是正方形,故C 选项不符合题意;若90ABC ∠=︒,则四边形ABCD 是矩形,故D 选项符合题意;故选:D.2.如图所示,在ABC 中,在90ACB ∠=︒,CD 平分ACB ∠,DE AC ⊥于E,DF BC ⊥于F,求证:四边形CEDF 是正方形.【答案】∵CD 平分ACB ∠,,DE AC DF BC ⊥⊥,∴DE DF =,90DFC DEC ∠=∠=︒,又∵90ACB ∠=︒,∴四边形CEDF 是矩形,∵DE DF =,∴矩形CEDF 是正方形.3.矩形ABCD 四个内角平分线组成四边形MFNE ,求证:四边形MFNE 是正方形.【答案】 四边形ABCD 是矩形,90BAD ADC BCD ABC ∴∠=∠=∠=∠=︒,AD BC =,AM ,DM ,CN ,BN 分别是四个内角平分线,45BAE EAD ADM CDM DCN BCN CBN ABN ∴∠=∠=∠=∠=∠=∠=∠=∠=︒,AE BE ∴=,90AEB N DFC AMD ∴∠=∠=∠=∠=︒,∴四边形MFNE 是矩形,在ADM △和BCN △中,MAD CBN AD BC ADM BCN ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ASA ADM BCN ∴ ≌,AM BN ∴=,AM AE BN BE ∴-=-,EN EM ∴=,∴矩形MFNE 是正方形.4.如图,已知Rt△ABC 中,∠ACB=90°,先把△ABC 绕点C 顺时针旋转90°至△EDC 后,再把△ABC 沿射线BC 平移至△GFE,DE、FG 相交于点H.(1)判断线段DE、FG 的位置关系,并说明理由;(2)连接AG,求证:四边形ACEG 【答案】(1)DE⊥FG,理由见解析(2)见解析【详解】(1)解:DE⊥FG,理由如下:∵把△ABC 绕点C 顺时针旋转90°至△EDC,∴∠BAC=∠CED,∵把△ABC 沿射线BC 平移至△GFE,∴∠ABC=∠GFE,∵∠BAC+∠ABC=90°,∴∠CED+∠GFE=90°,∴∠FHE=90°,∴DE⊥GF;(2)解:∵把△ABC 沿射线BC 平移至△GFE,∴AC=GE,AC∥GE,∴四边形ACEG 是平行四边形,∵把△ABC 绕点C 顺时针旋转90°至△EDC,∴AC=CE,∠ACE=90°,∴四边形ACEG 是正方形.5.如图:已知:AD 是ABC 的角平分线,DE AC ∥交AB 于E ,DF AB ∥交AC 于F .(1)求证:四边形AEDF 是菱形;(2)当ABC 满足什么条件时,四边形AEDF 是正方形?【答案】(1)见解析(2)90BAC ∠=︒【详解】(1)解:证明://DE AC ,//DF AB ,//DE AF ∴,//DF AE ,∴四边形AEDF 是平行四边形(有两组对边相互平行的四边形是平行四边形),EAF EDF ∴∠=∠(平行四边形的对角相等);又AD 是ABC ∆的角平分线,∴∠EAD=∠FAD,∵DE∥AC,∴∠EDA=∠FAD,EAD EDA ∴∠=∠,AE DE ∴=(等角对等边),∴四边形AEDF 是菱形(邻边相等的平行四边形是菱形);(2)解:由(1)知,四边形AEDF 是菱形,当四边形AEDF 是正方形时,90EAF ∠=︒,即90BAC ∠=︒,ABC ∴∆的90BAC ∠=︒时,四边形AEDF 是正方形.课后练习1.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,下列说法错误的是()A.若AC⊥BD,四边形ABCD是菱形B.若AB=BC,AC=BD,四边形ABCD是正方形C.若AC=BD,四边形ABCD是矩形D.若∠ABC=90°,四边形ABCD是正方形【答案】D【详解】解:∵四边形ABCD的对角线AC,BD相交于点O,且OA=OC,OB=OD,∴四边形ABCD为平行四边形.A.∵AC⊥BD,∴平行四边形ABCD是菱形,故该选项不符合题意;B.∵AB=BC,∴平行四边形ABCD是菱形,∵AC=BD,∴菱形ABCD是正方形;故该选项不符合题意;C.∵AC=BD,∴平行四边形ABCD是矩形,故该选项不符合题意;D.∵∠ABC=90°,∴平行四边形ABCD是矩形,故该选项符合题意;故选:D.2.如图,在正方形ABCD外作等边ADE∠=︒.,则BED【答案】45【详解】解: 四边形ABCD 是正方形,90BAD ∴∠=︒,AB AD =,又ADE 是等边三角形,AE AD ∴=,60AED DAE ∠=∠=︒,AB AE ∴=,9060150BAE ∠=︒+︒=︒,15ABE AEB ∴∠=∠=︒.BED AED ABE ∴∠=∠-∠45=︒,故答案为45∶.3.如图,在正方形ABCD 中,E,F 是对角线BD 上的点,且AB BF DE ==,求EAF ∠的度数.【答案】45︒【详解】解:在正方形ABCD 中,AB AD =,90BAD ∠=︒,45ABD ADB ∠=∠=︒.又∵AB BF DE ==,∴AD DE =,AB BF =,∴18(27)06.5DAE DEA ADB ∠=∠=︒-∠÷=︒,18(27)06.5BAF BFA ABD ∠=∠=︒-∠÷=︒,∴180180267.545EAF BFA DEA ∠=︒-∠-∠=︒-⨯︒=︒.4.如图,在正方形ABCD 中,延长BC 至E ,使CE CA =.求CAE ∠的度数.【答案】22.5︒【详解】解: 在正方形ABCD 中,90BCD ∠=︒,对角线AC 平分BCD ∠,∴90DCE BCD ∠=∠=︒,45ACB ∠=︒,CE CA =,ACE ∴ 是等腰三角形,ACB ∠ 是ACE △的一个外角,2ACB CAE E CAE ∴∠=∠+∠=∠,即245CAE ∠=︒,解得22.5CAE ∠=︒,故答案为:22.5︒.5.在正方形ABCD中,两条对角线相交于O,∠ACD的平分线交BD于P,若正方形ABCD的周长是16cm,则PB=___________cm.【答案】46.如图,正方形ABCD 的面积为2,菱形AMCN 的面积为1,则,M N 两点间的距离为()A.1B.2【答案】A【详解】解:如图,连接AC ,∵正方形ABCD 的面积为2,∴2122AC =,解得:2AC =,∵菱形AMCN 的面积为1,∴⋅=112AC MN ,即⨯⨯=1212MN ,解得:1MN =.故选:A.7.如图,已知正方形ABCD ,E 是AD 上一点,过BE 上一点O 作BE 的垂线,交AB 于点G ,交CD 于点H .6BE =,则GH =.【答案】6【详解】解:过点A 作GH 的平行线,交DC 于点F,如图所示:∵ABCD 是正方形,∴AG FH ∥,BA AD =,90BAE D ∠=∠=︒,∴90FAD AFD ∠+∠=︒,∵GH BE ⊥,AF GH ∥,∴AF BE ⊥,四边形AFHG 是平行四边形,∴90FAD BEA ∠+∠=︒,∴BEA AFD ∠=∠,∴()AAS BAE ADF ≌,∴BE AF =,∴GH AF =,∴6GH BE ==,故答案为:6.8.如图,直线1l ,2l ,3l 分别过正方形ABCD 的三个顶点A ,D ,C ,且相互平行,若1l ,2l 的距离为1,2l ,3l 的距离为2,则正方形的边长为.【详解】解∶如图,过点D 作1EF l ⊥交1l 于点E,交3l 于点F,∵123l l l ∥∥,∴32,EF l EF l ⊥⊥,∴90AED ADC CFD ∠=∠=∠=︒,1,2DE DF ==,∴90,90ADE DAE ADE CDF ∠+∠=︒∠+∠=︒,∴DAE CDF ∠=∠,∵四边形ABCD 是正方形,∴AD CD =,∴ ≌ADE DCF ,∴2,1AE DF DE CF ====,AD ==9.如图,有三个正方形ABCD ,DEFG ,FHMN ,点B ,C ,G ,H ,M 都在同一直线l 上,若正方形ABCD ,DEFG 的面积分别为3和8,则正方形FHMN 的面积为()A.4B.5C.6D.11【答案】B 【详解】解:∵四边形ABCD ,DEFG ,FHMN 都是正方形,∴DG FG =,90DCG GHF DGF ∠∠∠===︒;∴90CDG CGD CGD HGF ∠∠∠∠+=+=︒,∴CDG HGF ∠∠=,∴CDG HGF ≌(AAS ),∴CD GH =,CG FH =,∵正方形ABCD ,DEFG 的面积分别为3和8,∴2238CD DG ==,,∴正方形FHMN 的面积22835FH CG ===-=.故选∶B.10.若正方形的边长为a ,M 是BC 的中点,则图中阴影部分的面积是多少?【答案】213a 【详解】解:设ABE S S =△,M 是BC 中点,又因为ABE 和△同高,∴12BME S S =△,2311244AMB ABCD S S S a ===△正方形,则216S a =,∴阴影部分的面积2211263a a =⨯=.11.如图,正方形ABCD 的边长为2,H 在CD 的延长线上,四边形CEFH 也为正方形,则△DBF 的面积为()A.4C.D.2【答案】D 【详解】解:设正方形CEFH 的边长为a,根据题意得:21114422222()()BDF S a a a a a ∆=+-⨯---+22211222a a a a a =+-+--=2.故选:D.12.如图,在矩形ABCD 中,BE 平分ABC ∠,CE 平分DCB ∠,//,//BF CE CF BE .求证:四边形BFCE 是正方形.【答案】∵//,//BF CE CF BE ,∴四边形BECF 是平行四边形.∵四边形ABCD 是矩形,∴90ABC ∠=︒,90DCB ∠=︒.又∵BE 平分ABC ∠,CE 平分DCB ∠,∴1145,4522EBC ABC ECB DCB ∠=∠=︒∠=∠=︒.∴EBC ECB ∠=∠.∴EB EC =.∴BECF 是菱形(菱形的定义).在EBC 中,∵45,45EBC ECB ∠=︒∠=︒,∴90BEC ∠=︒.∴菱形BECF 是正方形(有一个角是直角的菱形是正方形).13.如图,ABC 中,AB AC =,AD 是BAC ∠的角平分线,点O 为AB 的中点,连接DO 并延长到点E,使OE OD =.连接AE ,BE .(1)求证:四边形AEBD 是矩形;(2)当90BAC ∠=︒时,猜想四边形AEBD 是什么图形?说明理由.【答案】(1)证明:∵点O 为AB 的中点,OE OD =,∴四边形AEBD 是平行四边形,AB AC = ,AD 是BAC ∠的角平分线,AD BC ∴⊥,90ADB ∴∠=︒,∴平行四边形AEBD 是矩形;(2)解:当90BAC ∠=︒时,四边形AEBD 是正方形,理由如下:AB AC = ,AD 是BAC ∠的角平分线,BD CD ∴=,90BAC ∠=︒ ,12AD BC BD \==,由(1)可知,四边形AEBD 是矩形,∴矩形AEBD 是正方形.14.已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.(1)求证:△BCG≌△DCE;(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.【答案】(1)证明:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°.∵∠BCD+∠DCE=180°,∴∠BCD=∠DCE=90°.又∵CG=CE,∴△BCG≌△DCE.(2)解:四边形E′BGD是平行四边形.理由如下:∵△DCE绕D顺时针旋转∴CE=AE′.∵CE=CG,∴CG=AE′.∵四边形ABCD是正方形,∴BE′∥DG,AB=CD.∴AB﹣AE′=CD﹣CG.即BE′=DG.∴四边形E′BGD是平行四边形.15.已知:如图,在ABC中.(1)分别以AB 、AC 为边向形外作正方形ABDE 、ACFG .求证:①CE BG =;②CE BG ⊥;(2)分别以AB 、AC 为边向形外作正三角形ABD △、ACE △.求证:①CD BE =;②求CD 和BE 所成的锐角的度数.【答案】证明:①在正方形ABDE ACFG 中,AE AB =,AC AG =,90EAB GAC ∠=∠=︒,∴EAC BAG ∠=∠,在EAC 和BAG △中,EA BA EAC BAG AC AG =⎧⎪∠=∠⎨⎪=⎩,∴()SAS EAC BAG ≌,∴CE BG =,②如图,记BG ,CE 的交点为H ,BG ,AC 的交点为T ,∵EAC BAG △≌△,∴ACE AGB ∠=∠,∵90AGT ATG ∠+∠=︒,ATG CTH ∠=∠,∴90ACE CTH ∠+∠=︒,∴1809090GHC ∠=︒-︒=︒,∴CE BG ⊥.(2)①如图,记CD ,BE 的交点为O ,∵等边ABD △和等边ACE△∴AE AC =,AD AB =,60CAE BAD ADB ABD ∠==∠=∠=︒,∵BAE BAC CAE ∠=∠+∠,CAD BAC BAD ∠=∠+∠,∴BAE CAD ∠=∠,∴ABE ADC △≌△,∴CD BE =;②∵ABE ADC△≌△∴ABE ADC ∠=∠,∴60BDO ABE BDO ADC ADB ∠+∠=∠+∠=∠=︒∴()18018060DOB DBO BDO ABD ABE BDO ∠=︒-∠-∠=︒-∠-∠+∠=︒∴CD 和BE 所成的锐角的度数为60︒.16.在学习对称的知识点时,我们认识了如下图所示的“将军饮马”模型求最短距离.问题提出:(1)如图1所示,已知A,B 是直线l 同旁的两个定点.在直线l 上确定一点P,并连接AP 与BP ,使PA PB +的值最小.问题探究:(2)如图2所示,正方形ABCD 的边长为2,E 为AB 的中点,P 是AC 上一动点.连接EP 和BP ,则PB PE +的最小值是___________;问题解决:(3)某地有一如图3AOB ,已知45AOB ∠=︒,P 是AOB 内一点,连接PO 后测得10PO =米,现当地政府欲在三角形空地AOB 中修一个三角形花坛PQR ,点Q R ,分别是OA OB ,边上的任意一点(不与各边顶点重合),求PQR 周长的最小值.【详解】(1)解:如图所示,当P 点在如图所示的位置时,PA PB +的值最小;(2)解:如下图所示,∵四边形ABCD 是正方形,∴AC 垂直平分BD ,∴PB PD =,由题意易得:PB PE PD PE DE +=+≥,当D、P、E 共线时,在ADE V 中,根据勾股定理得,DE =(3)解:如下图所示,分别作点P 关于OA ,OB 的对称点M N ,,连接OM ON MN ,,,MN 交OA ,OB 于点Q R ,,连接PR PQ ,,此时PQR 周长的最小值等于MN .由轴对称性质可得,10OM ON OP MOA POA NOB POB ===∠=∠∠=∠,,,∴224590MON AOB ∠=∠=⨯︒=︒,在Rt MON △中,MN =即PQR 周长的最小值等于。
《正方形的判定》的教学设计
教学目的:使学生掌握正方形的定义、性质和判定,会用正方形的概念和性质进行有关的论证和计算,理解正方形与平行四边形、矩形、菱形的内在联系和区别,进一步加深对“特殊与一般的认识。
教学重点:正方形的定义.
教学难点:正方形与矩形、菱形间的关系.
教学方法:双边合作如:在教学时可播放转换动画使学生获得生动、形象的可视思维过程,从而掌握判定一个四边形是正方形的方法.为了活跃学生的思维,可以得出下列问题让学生思考:
(1)对角线相等的菱形是正方形吗?为什么?
(2)对角线互相垂直的矩形是正方形吗?为什么?
(3)对角线垂直且相等的四边形是正方形吗?为什么?如果不是,应该加上什么条件?
(4)能说“四条边都相等的四边形是正方形”吗?为什么?
(5)说“四个角相等的四边形是正方形”,对吗?
教学过程:
让学生将事先准备好的矩形纸片,按要求对折一下,裁出正方形纸片.
问:所得的图形是矩形吗?它与一般的矩形有什么不同?
所得的图形是菱形吗?它与一般的菱形有什么不同?
所得的图形在小学里学习时称它为什么图形?它有什么特点?
由此得出正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
(一)新课
由正方形的定义可以得知:正方形是有一组邻边相等的矩形,又是有一个角是直角的菱形,因此正方形具有矩形的性质,同时又具有菱形的性质.
请同学们推断出正方形具有哪些性质?
性质1、(1)正方形的四个角都是直角。
(2)正方形的四条边相等。
性质2、(1)正方形的两条对角线相等。
(2)正方形的两条对角线互相垂直平分。
(3)正方形的每条对角线平分一组对角。
例1 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.已知:四边形ABCD是正方形,对角线AC、BD相交于点O.
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=CO=BO=DO
(正方形的两条对角线相等,并且互相垂直平分).
∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,并且△ABO≌△
BCO≌△CDO≌△DAO.
问:如何判定一个四边形是正方形呢?
正方形的判定方法:
1.先判定四边形是矩形,再判定这个矩形是菱形;
2.先判定四边形是菱形,再判定这个菱形是矩形.
例2 已知:如图,点A′、B′、C′、D′分
别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′.
求证:四边形A′B′C′D′是正方形.
分析:根据正方形的四条边相等,四个角都是直角及已知条件,可以得到四个全等的直角三角形,它们的斜边都相等,从而判定四边形A′B′C′D′是菱形,再利用直角三角形两锐角互余证明菱形是矩形.
证明:(略)
(二)练习
1.已知正方形的边长为2cm,求这个正方形的周长、对角线长和正方形的面积.
2.正方形的对角线和它的边所成的角是多少度?为什么?
3.如果一个菱形的两条对角线相等,那么它一定是正方形,为什么?
4.如果一个矩形的两条对角线互相垂直,那么它一定是正方形,为什么?
三小结
矩形、菱形、正方形都是特殊的平行四边形而且正方形还是特殊的矩形、特殊的菱形,它们的包含关系如图:
四作业
1.已知正方形的一条对角线长4cm,求它的边长和面积.
2.两条对角线互相垂直平分且相等的四边形是正方形.
3.求证:正方形对边中点的连线将正方形分成四个小正方形.
4.求证:矩形的各内角平分线组成的四边形是正方形.。