2-3 管槽内层流对流换热特征
工程上存在大量的管槽内对流换热问题。
本节对管槽内层流强制对流换热的流动与换热特征进行分析。
一、流动特征
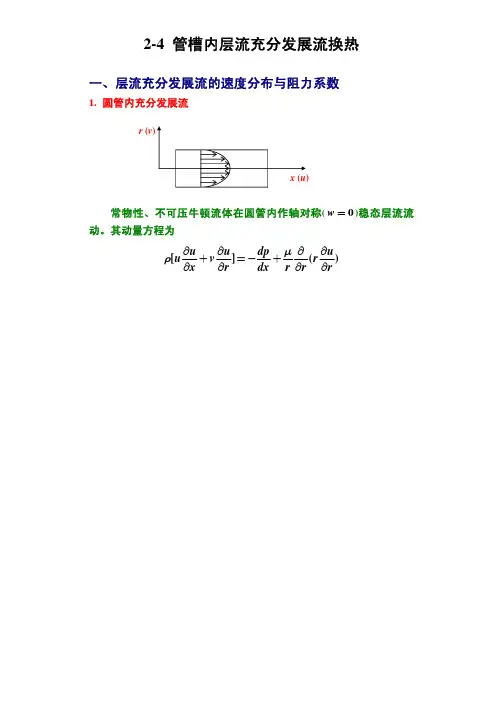
当流体以截面均匀的流速0u 进入管道
后，由于粘性，会在
管壁上形成边界层。
边界层内相同r 处的轴向流速随δ的增加
而降低，导致对管中心势流区的排挤作用，使势流区流速增加。
当边界层厚度δ达到管内半径时，势流区消失，边界层汇合于管轴线处，同时截面内速度分布不再变化。
u o
将管入口截面至边界层汇合截面间的流动区域称为入口段，或称为未充分发展流、正在发展流。
该区域内，速度分布不断变化，
(,)u u x r =，同时存在径向速度(,)v x r 。
边界层汇合截面以后的流动速度不再变化，()u u r =，而径向速度
0v =，这段流动区域称为充发展段或充分发展流。
所以，管内流动存在特征不同的两个区域：入口段，充分发展段。
充分发展流动又分为：简单充分发展流、复杂充分发展流两种。
1). 简单充分发展流
是指只存在轴向速度分量，而其它方向速度分量为零的充分发展流动。
对圆管： ()u u r =，0v w ==； 对矩形管道：(,)u u x y =，0v w ==。
简单充分发展流任意横截面上压力均匀，沿轴向线性变化，即
dp
const dx
=
证明：对简单充分发展流，径向速度0v =，根据径向动量方程：
222211()v v p v v v u v x r r r r x r
νρ∂∂∂∂∂∂+=−+++∂∂∂∂∂∂ ⇒ 0p r ∂=∂，
即任意横截面上压力均匀，压力仅沿轴向变化。
于是，轴向动量方程为：
222211(u u dp u u u
u v x r dx r r x r
νρ∂∂∂∂∂+=−+++∂∂∂∂∂
又发展流0u
x
∂=∂（速度分布不变，或由连续方程得出）⇒
220u
x
∂=∂、()u u r =。
动量方程变为：
2
21()dp u u dx r r r
ρν∂∂=+∂∂ 由于上式右端与与x 无关，所以必然有：
dp
dx
=常数，而与x 无关，或说压力沿轴向线性分布。
2). 复杂充分发展流
是指在垂直于流动方向的截面上，速度分量v 、w 不为零，但不
随x 变化，即：
0u x
∂=∂，而且0v w
x x ∂∂==∂∂。
譬如：矩形管道中的湍流充分发展流、弯曲管道中的充分发展流(二次环流)，以及受浮力影响的充分发展流等。
工程中的充分发展流动大多属于复杂充分发展流，但分析较困难，理论研究时多简化为简单充分发展流。
3). 简单充分发展流动的主要特征
(a). 沿流动方向的速度分布不变：0u
x
∂=∂； (b). 横截面内速度分量为零：0v w ==；
(c). 沿流动方向的压力梯度为常数：dp
const dx =；
(d). 局部摩擦系数f c 不随x 变化，即Re f c const ⋅=；
(e). 圆管及平行平板通道内速度分布呈抛物线状(Poiseullie 分布)。
二、管槽内层流换热特征
与流动类似，管槽内换热也存在特征不同的两个区域。
温度均匀的流体进入管道后，形成热边界层，其温度分布发生变化。
边界层内温度由w T 向0T 过渡，中心势流区维持入口温度0T ，当热边界层汇合后，整个截面上的温度都开始发生变化，但其无量纲温度分布不再变化，即截面内各点的温度保持按一定规律同步变化，这导致流体与壁面的换热强度不变化。
o w T T −
我们把热边界层汇合前的区域称为热起始段(热正在发展流，thermally developing flow)，而把热边界层汇合后的区域称为热充分发展段(热充分发展流，thermally developed flow)。
1. 热起始段特征
由于热边界层正在形成发展，且横截面内存在径向流动使其换热强度高，对流换热系数由入口开始逐渐下降。
2. 热充分发展段特征
由于热边界层已充分发展，各截面内无量纲温度分布相同，换热强度不变，即：
(a).
(0w
w
T T x T T −∂Θ∂==∂∂−； (b).x h const = ( 对w q const =与w T const =情况)
证明： x w r R
T
h T T r
=∂=
⋅−∂λ
式中， ()()w w w w T T T T T T T r r T r
∂−−∂∂Θ
=⋅=−∂∂−∂ 于是，
x r R
h r λ=∂Θ
=∂
又
0x
∂Θ
=∂，即()f r Θ=；所以r R const r =∂Θ=∂；从而证明： x x r R h d Nu d const r λ
=∂Θ=
=⋅=∂ (2.3.2)
(c). 温度分布特征
由w
w
T T T T −Θ=
−，这里(,)T T x r =、()w w T T x =、()T T x =, 得： (,)()[)()]w w T x r T x T x T x =+Θ−
[]()w w w dT dT T dT T T x dx dx dx x
∂∂Θ
=+Θ−+−∂∂
由0x
∂Θ
=∂得: []w w
T dT dT dT x
dx dx dx ∂=+Θ⋅−
∂ 对w q const =，w T const =两种情况，有温度分布特殊关系。
∆∆
w q const =时：
由(w x w q h T T =− ⇒ ()()w
w x
q T x T x const h −==，求导得：
0w
dT dT dx dx
−= 则:
(,)()()w T x r dT x dT x x
dx dx ∂===∂常数 (2.3.3) 上式表明，在w q const =情况下：管内充分发展流的轴向温度变化率与径向位置r 无关。
通过热平衡分析可得出该轴向温度变化率常数值。
考虑一微元段：
2
2w p q R dx R u c dT ππρ⋅⋅=⋅⋅， 得：
2w p
q dT dx Ru c ρ= (2.3.4) (,)()()w T x r dT x dT x x dx dx ∂===∂2w p
q Ru c ρ (2.3.5)
220T
x
∂=∂ (2.3.6) 即：w q const =时，管内充分发展流的轴向温度线性分布，与r 无关。
则能量方程中，轴向的导热项或沿轴向导热的影响为零，但
0x T q x
λ∂=−≠∂。
相应地，
轴向动量扩散影响为零。
将2w p q dT dx c uR
ρ=积分⇒ 02()w
p q T x T x c uR
ρ=+
⋅ (2.3.7)
∆∆ w T const =时： 0w
dT dx
=，有： (,)w w T T T x r dT dT
x dx T T dx
−∂=Θ⋅=⋅∂− (2.3.8) 即：w T const =时，轴向温度梯度与r 有关。
∆
其换热温差 ()()w T T x T x ∆=−按指数规律衰减。
由能量平衡：
2
2x p h T Rdx c u R dT πρπ⋅∆⋅=⋅⋅
即 2()
x w p dT h T T dx c u R
ρ⋅−=⋅ 或
2x p d T h dx T c u R ρ∆=−∆⋅ 积分
⇒
2T
x
x
p T d T h dx T c u R
ρ∆∆∆=−∆⋅∫
∫ ⇒
00()()2()exp()(0)w x w p T x T x h T x x T T T c uR
ρ−∆==−⋅∆− (2.3.9)。
