高等传热学讲义
- 格式:pps
- 大小:791.00 KB
- 文档页数:52

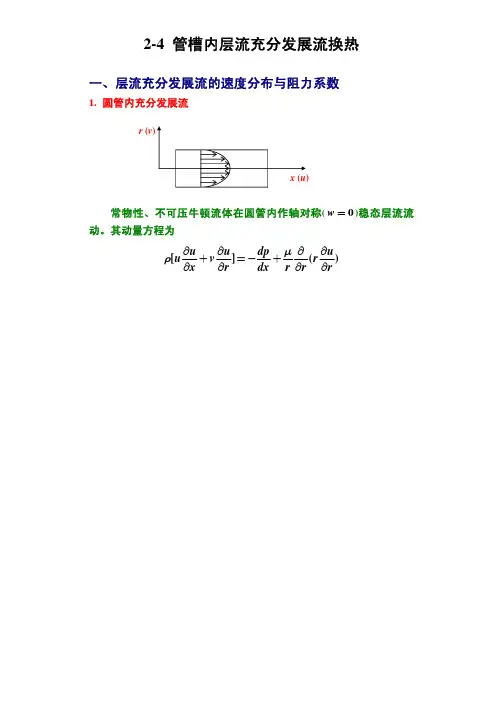
)(2=Φ+∇=Φ+∇∙∇∙∙λλt t )(12133212dx dt h h h dx d h h h t =∇高等传热学稳态导热第二讲: 稳态导热 1. 控制方程:B a s i c E q s当导热系数为常量时:P o i s s i o n E q . v 当 1-D 时: 其中拉梅系数 h 1,h 2,h 32.1D ,有内热源,3r d B .C 时的解 【1】1D ,内热源为常数,3r d B .C 时的解若沿传热方向r 传热面积A 的变化规律为A =C r n ,有边界条件:其解为: 2222(1)R r t t m hR R λλ∞Φ-=+- 其中: n m =2(n +1) V /A =R /(n +1)0 2 R 1 4 R /2 2 6 R /3202(1)R t t m hRλλ∞Φ-=+在r=R(外表面)处的温度: 2w R t t hm ∞Φ-= 导热体最大温差:20w R t t m λΦ-= 。
温差正负取决于内热源,加热为正,吸热为负。
外表面热流与内热源关系:/()/(1)w w q V A h t t R n ∞=Φ=-=Φ+ Spheren Cylinder n Plate n dr dt r n dr t d 210022====Φ++∙λ0,0,()w dt r dr dt hr R t t dr λ∞====--当h =∞, t ∞=t w :相当于外表面是第一类边界条件222(1)R r t t m Rλ∞Φ-=-【2】.1D ,内热源为温度线性函数a bt Φ=+ ,3r d B .C 时的解: 一般有:20t a bt λ∇++=,叫H e l m h o t z e q s将:a bt Φ=+ 代入H e l m h o t z e q s ,得:2/0b λ∇Φ+Φ= 。
1D :220d n d b dr r dr λ∙∙∙ΦΦΦ++=))A B Φ=+ 平壁 B =0, /()))A h h ∞=Φ- 00))AJ BY Φ=+ 圆筒壁 B =0, ))A B Φ=+ 可用于通电导线、核燃料的计算。



第一章 导热理论基础本章重点:准确理解温度场、温度梯度、导热系数等基本概念,准确掌握导热基本定律及导热问题的基本分析方法。
物质内部导热机理的物理模型:(1)分子热运动;(2)晶格(分子在无限大空间里排列成周期性点阵)振动形成的声子运动;(3)自由电子运动。
物质内部的导热过程依赖于上述三种机理中的部分项,这几种机理在不同形态的物质中所起的作用是不同的。
导热理论从宏观研究问题,采用连续介质模型。
第一节 基本概念及傅里叶定律1-1 导热基本概念一、温度场(temperature field)(一)定义:在某一时刻,物体内各点温度分布的总称,称为即为温度场(标量场)。
它是空间坐标和时间坐标的函数。
在直角坐标系下,温度场可表示为:),,,(τz y x f t = (1-1)(二)分类:1.从时间坐标分:① 稳态温度场:不随时间变化的温度场,温度分布与时间无关,0=∂∂τt ,此时,),,(z y x f t =。
(如设备正常运行工况) 稳态导热:发生于稳态温度场中的导热。
② 非稳态温度场:随时间而变化的温度场,温度分布与时间有关,),,,(τz y x f t =。
(设备启动和停车过程)非稳态导热:在非稳态温度场中发生的导热。
2.从空间坐标分: ① 三维温度场:温度与三个坐标有关的温度场,⎩⎨⎧==稳态非稳态),,(),,,(z y x f t z y x f t τ ② 二维温度场:温度与二个坐标有关的温度场,⎩⎨⎧==稳态非稳态),(),,(y x f t y x f t τ∆tt-∆tgrad t③ 一维温度场:温度只与一个坐标有关的温度场,⎩⎨⎧==稳态非稳态,)()(x f t x f t τ 二、等温面与等温线1.等温面(isothermal surface):在同一时刻,物体内温度相同的点连成的面即为等温面。
2.等温线(isotherms):用一个平面与等温面相截,所得的交线称为等温线。
为了直观地表示出物体内部的温度分布,可采用图示法,标绘出物体中的等温面(线)。

第2章边界层方程第一节Prandtl 边界层方程一.边界层简化的基本依据外:粘性和换热可忽略)(t δδ,l l t <<<<δδ或内:粘性和换热存在)(t δδ特征尺寸—l二.普朗特边界层方程常数性流体纵掠平板,层流的曲壁同样适用)。
δvlu ∞∞∞u lv v l u δδ~~,可见,0=∂∂+∂∂yv x u )()((x x R δ>>曲率半径yxuv∞∞T u ,wT ∞∞T u ,δl)(12222yu x u x p y u v x u u ∂∂+∂∂+∂∂-=∂∂+∂∂νρδδ∞∞u u llu u ∞∞2l u ∞ν2δν∞u )(2lu ∞除以无因次化11Re12))(Re 1(δl因边界层那粘性项与惯性项均不能忽略,故项可忽略,且说明只有Re>>1时,上述简化才适用。
)(12222yv x v y p y v v x v u ∂∂+∂∂+∂∂-=∂∂+∂∂νρ1~))(Re 1(2δllδ;可见2222xuy u ∂∂>>∂∂δδ1)(2∞u l l u lu /)(∞∞δ2/)(lu l ∞δν2/)(δδν∞u l :除以lu 2∞)(Re 1lδ))(Re 1(δl lδ可见,各项均比u 方程对应项小得多可简化为于是u 方程压力梯度项可写为。
)(2222yTx T a y T v x T u ∂∂+∂∂=∂∂+∂∂,0=∂∂yp dxdpρ1-),(lδ乘了δθδwu l )(∞lu w θ∞2lawθ除以:lu w θ∞Pe/12)(/1δlPe 12δθwa 1)(∞-=T T w w θPr)Re (⋅====∞∞贝克列数—导热量对流热量w w p lk u c a l u Pe θθρ边界层方程:。
时或当可忽略可见,)1,1~)(1(222>>∂∂Pe l Pe x T a δ0=∂∂+∂∂yvx u )(12222yu x u x p y u v x u u ∂∂+∂∂+∂∂-=∂∂+∂∂νρ)(2222yT x T a y T v x T u ∂∂+∂∂=∂∂+∂∂其中,压力的变化由主流速度的变化确定:,0=∴=∞dxdpdx du 对于平板,gf e d c b a y x yy xy xx =+++++φφφφφφ(主流柏努利方程)dxdu u dx dp ∞∞=ρ1(主流速度可按势流问题求解得到)二.普朗特边界层方程定义:对于二元二阶线性偏微分方程(a 、b 、c 、d 、e 、f 、g 均为x ,y 的已知函数)当,称为双曲型的,(无粘超音速流问题);当,称为抛物型的;当,称为椭圆型的。




第2章边界层方程第一节Prandtl 边界层方程一.边界层简化的基本依据外:粘性和换热可忽略)(t δδ,l l t <<<<δδ或内:粘性和换热存在)(t δδ特征尺寸—l二.普朗特边界层方程常数性流体纵掠平板,层流的曲壁同样适用)。
δvlu ∞∞∞u lv v l u δδ~~,可见,0=∂∂+∂∂yv x u )()((x x R δ>>曲率半径yxuv∞∞T u ,wT ∞∞T u ,δl)(12222yu x u x p y u v x u u ∂∂+∂∂+∂∂-=∂∂+∂∂νρδδ∞∞u u llu u ∞∞2l u ∞ν2δν∞u )(2lu ∞除以无因次化11Re12))(Re 1(δl因边界层那粘性项与惯性项均不能忽略,故项可忽略,且说明只有Re>>1时,上述简化才适用。
)(12222yv x v y p y v v x v u ∂∂+∂∂+∂∂-=∂∂+∂∂νρ1~))(Re 1(2δllδ;可见2222xuy u ∂∂>>∂∂δδ1)(2∞u l l u lu /)(∞∞δ2/)(lu l ∞δν2/)(δδν∞u l :除以lu 2∞)(Re 1lδ))(Re 1(δl lδ可见,各项均比u 方程对应项小得多可简化为于是u 方程压力梯度项可写为。
)(2222yTx T a y T v x T u ∂∂+∂∂=∂∂+∂∂,0=∂∂yp dxdpρ1-),(lδ乘了δθδwu l )(∞lu w θ∞2lawθ除以:lu w θ∞Pe/12)(/1δlPe 12δθwa 1)(∞-=T T w w θPr)Re (⋅====∞∞贝克列数—导热量对流热量w w p lk u c a l u Pe θθρ边界层方程:。
时或当可忽略可见,)1,1~)(1(222>>∂∂Pe l Pe x T a δ0=∂∂+∂∂yvx u )(12222yu x u x p y u v x u u ∂∂+∂∂+∂∂-=∂∂+∂∂νρ)(2222yT x T a y T v x T u ∂∂+∂∂=∂∂+∂∂其中,压力的变化由主流速度的变化确定:,0=∴=∞dxdpdx du 对于平板,gf e d c b a y x yy xy xx =+++++φφφφφφ(主流柏努利方程)dxdu u dx dp ∞∞=ρ1(主流速度可按势流问题求解得到)二.普朗特边界层方程定义:对于二元二阶线性偏微分方程(a 、b 、c 、d 、e 、f 、g 均为x ,y 的已知函数)当,称为双曲型的,(无粘超音速流问题);当,称为抛物型的;当,称为椭圆型的。
042>-ac b 042=-ac b 042<-ac b抛物型方程特点例:一维非稳态导热22xT a t T ∂∂=∂∂无影响,对,则坐标:若)()(1212t T t T t t t >t 称为单向坐标。
x 称为双向坐标。
的、受两侧温度坐标:)()()(210x T x T x T x 1x 0x 2x )(1x T )(0x T )(2x T椭圆型问题特点例:二维非稳态导热02222=∂∂+∂∂yTx T某一点的温度受其周围各点温度的影响,x 、y 均为双向坐标。
椭圆型问题必须整场求解。
1.u 方程特点:①抛物型方程,x 为单向坐标。
②p(x)为已知函数,或由势流方程求得。
未知量只有u 、v 。
2.T 方程特点:①也是抛物型的,x 为单向坐标。
②常物性且速度场已知时,为线性方程。
第二节粘性流体匹配渐进展开理论简介一.Prandtl边界层理论的不足1.Re不很大时,略去纵向扩散会造成较大误差,且修正办法不明。
2.只考虑了外流对边界层的影响,未考虑边界层对外流的影响。
二.匹配渐进展开法第三节旋转对称和轴对称边界层方程)()(x x r δ>>0=∂∂θ。
可认为离轴距离仍为,由于微元体离壁距离)()(x r x r y <<0=θv 旋转对称:旋成体轴对称:进一步有∞∞T u ,yδx)(x r θ第四节圆管内的边界层方程式(2.30),(2.32)第五节边界层积分方程例:壁面有喷注或吸入的轴对称旋成体边界层连续性积分方程和能量积分方程:壁面喷入:顶面流入:⎰=Yx urdyM 0ρrdx v w w ρrdx v dx urdy dx d w w Yρρ-=⎰][0rdx v M dx dxdM M M w w x xx Y ρ--+=yx1=δθdx)(δ>Y rwv dx dxdrr +dxurdy dx d urdy dx dx dM M M YY x x dxx ][00⎰⎰+=+=+ρρp dxdxdp p +δθr δθdx dxdr21δθdx dxdr21p dx pdx能量积分方程:忽略宏观运动动能的变化;不可压缩流和理想气体。
顶面流入:壁面传入:由能量守恒关系得:对于一般可压缩流,且宏观动能变化不可忽略时,则要将式中换成。
⎰=Yp x uTrdyc E 0ρ)(])([10∞∞∞∞---=⎰T C T C v rdy T C T C u dx d r q p w pw w w Yp p w ρρrdxT C v q w pw w w w )(ρ+λT C p dxuTrdy c dx d uTrdy c dx dx dE E E Yp Y p x x dx x ][00⎰⎰+=+=+ρρrdxT C v dx rdy uT c dx d T C M p w w Yp p Y ∞∞∞∞∞∞-=⎰ρρ][0221u H +第3章非耦合外部层流边界层换热第一节求解边界层微分方程的经典方法——仿射相似一.仿射相似的概念例:半无限大物体非稳态导热精确解:热层厚度令,则,可见,x ,t 可综合为一个自变量,原偏微分方程可化为关于的常微分方程。
atx4=ηη)4(1),(0at xerf T T T t x T ii -=--at4∝δ)(),(0ηf T T T t x T ii=--)(ηT 1δ2δ3δxT iT ),(3t x T ),(2t x T ),(1t x T——相似性变量几何意义:t 时刻的温度分布线相当于将时刻的温度分布线保持纵坐标不变,横坐标按的比例变化而得到的曲线。
如果以为横坐标绘出分布图,则任何时刻的图形都相同,重合于一条曲线。
这样的分布图形称作仿射相似图形。
二.存在仿射相似的条件及相似变量的导出:结论:1.存在仿射相似的条件(速度场):边界层外缘速度:(绕流楔形体的势流速度满足这一规律)2t 11144at at x x ==δδηη)(ηT mCx x U =)(2.相似变量及方程:ηx x U yν)()(ηf 动量方程)(x xU νψxx U m yν)(21+)(12x xU m ν+ψ0)1(221='-+''+'''+f m f f f m 0)1(2='-+''+'''f f f f β12+=m m βm ,β只取决于楔夹角3.温度场仿射相似条件及能量方程:速度场仿射相似,以及=∞Tννx C T T w =-∞常数=w T 常数(或)且η)(ηθ能量方程x x U yν)(xx U m yν)(21+∞∞--T T T T w ∞∞--T T T T w 0Pr Pr 21='-'+''θγθθf f 0Pr Pr 12='-'+''+θθθγf f m 0)1(Pr Pr 12=-'-'+''+θθθγf f m 或)(常数=∞T )(常数=w T第二节纵向绕流平壁和楔形体的摩擦和换热)()0(2=∂∂''=y fxyU f C ηρμdxC l C lfx f ⎰=01221UC wx fx ρτ=1.摩擦求解动量方程(可用打靶法:P71-72),得到由及可得f f f '''、、0=∂∂=y wxyu μτ(局部)(平均);dx h l h lx ⎰=01khl Nu =k xT T q k x h Nu yTkq w wx x x y w ∞=-==∂∂-='以及由、0,ϑθ2.换热求解能量方程得到可得0)()0(=∂∂'=y x yx Nu ηθ3.速度场相似而壁温任意变化时利用能量方程为线性方程,满足迭加原理的特性进行求解。
(P97、98:式(3.35))第三节绕流物体滞止区域换热(驻点附近)二维滞止区:P83:图3.7;P94;轴对称滞止区:P99:图3.14,3.15第四节壁面有抽吸和喷注时的换热(P104~111)第5章通道内非耦合层流换热第一节流动起始段和充分发展段一.充分发展段(full developed flow )1.圆管基本特征:0=∂∂xu 0==θv v r (X 为流动方向)(简单充展流)Re f常数,==∂∂=∂∂=∂∂dxdp x p p r p 0θfx C Re f C 由基本特征可推出另外3个特征:①②圆管及平行平板通道速度分布为抛物面③或f与x无关,(或)=常数2.非圆截面通道与圆管充分发展流特性基本相同,但流速分布不再是抛物面型。
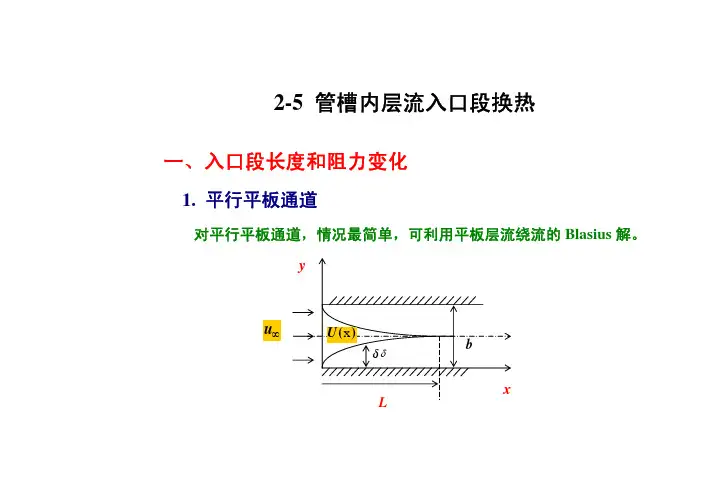
)]/()[(2s m kg ⋅质量流速e d μνeeav Gd d u ==Re W f d ce 4=其中,Reavcu f m G ρ== 数通常以当量直径定义:流通截面积—c f 湿周长—W二.流动起始段(developing flow )边界层型问题,一般不具有相似解,往往用近似法或数值法求解。
圆管::1500Re :1000Re 20===d d mmd68.184==d L h h L 056.0Re /1==C dL dh md L h 12.156==起始段长度:例:dfxC Redd x Re /056.01=C 起始段充分发展段第二节热起始段和充分发展段一.热充分发展段特征截面流体平均温度—b T0=∂Θ∂xbw w T T T T --=Θ⎰⎰=ApApb udAC uTdAC T ρρ基本特征:其中:常量=∂∂--=)(10r r b w rTT T无关常量,与x h x =常量,即=∂∂∴=0r r rΘ:),(0代入上式得而-b w x wx r r T T kh k q rT -==∂∂=常量常量,即==x xh kh )(,0r xΘΘΘ==∂∂即 可推出一下特征:①(1)cav p x c av p w b f u C TWh f u C Wq dx dT ρρ∆==时:C q w =dxdT dx dT C T T h q b w b w x w =∴=-=,)( 常量得:、再由式===∂∂dxdT dx dT x T bw )3()2()(0dxdT dx dT dx dT x T x b w w-Θ-=∂∂⇒=∂Θ∂②由以及微段热平衡式可得:a)(3)(2)T C dxTd ∆-=∆1时:C T w =xC i eT T 1-∆=∆p xc av p x C mWh f u C Wh C ==ρ1其中,按指数规律变化:或可得b T T ∆b)式(3)可改写为:再由式(2)可知:常量≠Θ=∂∂dxdT x Tb二.热起始段特征常数≠≠∂Θ∂x h x,0tL xxh 热起始段热充分发展段热起始段、或随的具体变化关系还取决于流动是否充分发展了。