下载文档原格式
高等传热学课件对流换热高等传热学课件对流换热一、概述湍流模型是半阅历、半理论的争论方法，其目的是将湍流的脉动相关项与时均量联系起来，使时均守恒方程封闭。
自1925年Prandtl提出混合长度理论，各国学者对湍流模型进行了大量争论，提出了许多模型。
W.C.Regnolds建议按模型中所包含的微分方程数目进行分类，成为目前适用的湍流模型分类方法。
一般将湍流模型分为：z 零方程模型（代数方程模型）z 一方程模型z 二方程模型z 多方程模型争论（Morkovin 莫尔科文）表明：当M5时，流体的可压缩性对湍流结构不起主导影响，因此我们仅参考不行压缩状况。
依据大量的试验争论结果，湍流边界层对流换热的强弱主要取决在内层区：由相像原理分析得出，Prt近似是一个常数（Prt≈0.9）这样，只要确定了νt，即可简洁地得到αt，所以在介绍湍流模型时，只给出νt或t时均量的关系式。
二、零方程模型（代数方程模型）零方程模型中不包含微分方程，而用代数关系式将νt与时均量关联起来。
Prandtl混合长度理论是最早的代数方程模型。
它适用于：充分进展的湍流剪切流边界层内层，y≤0.2δ。
对外层区，一些学者争论后仍沿用Prandtl混合长度的模型关系式：但，L=λδ（3.7.1）试验常数λ在0.08~0.09之间。
Von Kármán、Deissler、Van Driest、Taylor等人先后提出了更完善的代数方程模型。
(1) Von Kármán模型Von Kármán假设湍流内各点的脉动相像（局部相像），即各点之间只有长度尺度与空间尺度的.差别。
对平行流流场，若对某点（y0处）四周的时均速度进行Taylor开放：（a）若流淌相像，则必有尺度L与速度u0（u0＝u(y0)）使上式无量纲后成为通用分布。
u(y0)y令 Y=； U(Y)= u0L则有无量纲形式：（b）若上式是相像的通用速度分布，则式中各系数之比应与位置无关，而是一个常数。
对流部分思考题参考答案热动硕士1501 吕凯文1、简述对流换热问题的各种求解方法。
答：对流换热问题的求解方法有：（1）分析法，PDE ，B.L.PDE ，B.L.IDE 等；（2）实验法，相似理论，量纲分析；（3）比拟法，雷诺比拟，切尔顿－柯尔朋比拟，Plant Analogy, 卡门比拟；（4）数值法，差分法，有限元法等。
第二种答案：答：①数学解析法：理论求解或数值求解描述对流换热过程的微分方程组，得到精确解或相似解；②模拟实验法：根据相似理论，将描述对流换热过程的微分方程组通过数学、物理简化成准数方程的形式，然后根据实验确定准数方程的具体关系。
2、能量方程的五种表达形式；边界层微分方程的特点和前提条件。
答：能量方程的五种表达形式： ①总能形式的能量方程：W dxdydz q q q dxdydz D De s r +++∙-∇=*)(τρ ②热力学能形式的能量方程：ηφτρ+∙∇-++∙-∇=V P q q q D De s r ③焓形式的能量方程：i=e+P/ρηφττρ++++∙-∇=D DP q q q D Di s r ④定压比热形式的能量方程：ηφτβτρ++++∙-∇=D DP T q q q D DT C s r p P T)(1∂∂-=ρρβ体胀系数 ⑤定容比热形式的能量方程：ηφτρρ+∙∇∂∂-++∙-∇=V T P T q q q D DT C s r v)( 边界层微分方程的特点：前提条件：①流体为不可压缩的牛顿流体，稳定流动；②常物性，无内热源；③忽略由黏性摩擦而产生的耗散热。
3、相似原理理论求解对流换热问题的原理、步骤及应用。
答：原理：凡是相似的物理现象，其物理量的场一定可以用一个统一的无量纲的场来表示；凡是彼此相似的现象，描写该现象的同名特征数——准数对应相等。
步骤：①写出所写研究对象的微分方程组；②根据相似原理，利用置换的方法，找出相似准数；③将所研究的问题用准数方程的形式表示出来；④用物理实验的方法，找出准数函数的具体函数关系；⑤将函数关系推广应用。
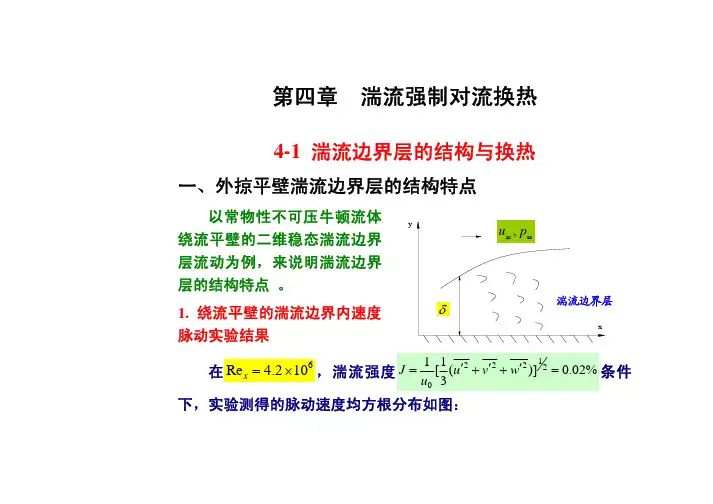
第四章 湍流强制对流换热4-1 湍流边界层的结构与换热一、外掠平壁湍流边界层的结构特点以常物性不可压牛顿流体绕流平壁的二维稳态湍流边界层流动为例，来说明湍流边界层的结构特点 。
1. 绕流平壁的湍流边界内速度脉动实验结果在6Re 4.210x =×下，实验测得的脉动速度均方根分布如图：y湍流边界层内脉动速度的均方根值变化由实验结果发现：a）由于受壁面束缚作用，壁面附近的脉动速度很小，时均速度梯度很大；（分子粘性应力占主导）。
b）随着离开壁面距离的增加，脉动速度增大，达到最大值后又减小，而时均速度分布趋于平坦；（雷诺应力增大又减小）。
c ）在沿壁面的法线方向上，湍流边界层可大致分为内层区和外层区两个区域，又称壁区和尾迹区。
d ）内层区约占边界层厚度的20％，（0.2y δ≤），内层区的大部分处于湍流状态，时均速度梯度较大。
在靠近壁面处，因受壁面影响，湍流脉动速度减小，雷诺应力大大减弱，粘性应力占主要作用，把壁区内紧靠壁面的这一薄层称为粘性底层；e ）在外层区，脉动受壁面影响较弱，湍流应力仍处主要作用，但由于时均速度梯度比内层区小，使外层区的湍流生成项所占比例也减小。
f ）外层区与边界层外主流区的界面并不整齐，存在着间歇的湍流脉动，随着接近主流，湍流脉动逐渐减小。
g ）实验还表明：在内层区，流线基本上平行于壁面，流动近似具有剪切流的特性，即沿x 方向，u2. 时均守恒方程组及在内层区的简化（4.1.1）采用Boussinesq假设，湍流附加应力为：（a）动量方程可写作：（4.1.2）式中，τ是湍流总应力，等于分子粘性应力与湍流附加应力之和。
（4.1.3）内层区流动的动量方程简化由连续性方程0u v x y ∂∂+=∂∂，对内层区流动，因其剪切流特性，0u x∂=∂，0v y∂⇒=∂，yv v dy y∂=∂∫ ⇒于是，动量方程：()u u u v x y yτρ∂∂∂+=∂∂∂可化简为：. w ττ⇒= （4.1.4）即：在内层区，湍流总应力与离开壁面的距离无关，等于壁面处的切应力w τ。
4-2 管内湍流充分发展流对流换热一、管内湍流充分发展流对常物性、不可压牛顿流体的管内湍流充分发展流，有：0ux∂=∂，0v =，0p r ∂=∂ 于是，其二维稳态的动量方程化简为：（4.2.1）（4.2.2） 积分得到：（4.2.3）上式表明：管内湍流充分发展流的总切应力沿径向是线性分布的。
当w r r =时，w ττ=，于是：（4.2.4）） 定义：y 是沿半径方向离开壁面的距离，则w y r r =−。
于是τ可表示为：y（4.2.4）采用无量纲参数：u u u τ+=, y u y τν+⋅=, u τ=（4.2.5）与平壁湍流边界层的无量纲速度关系式：（内层区）所以，管内湍流充分发展流的近壁区与扰流平壁的湍流边界近壁区都遵循通用速度分布。
△另外，在管内充分发展湍流中，不存在平壁湍流边界层边缘那.种间歇湍流脉动，因而，在近壁区外，速度分布规律偏离壁面规律不像平壁湍流边界层那样显著。
这样，可近似地用通用速度分布来描述整个管截面内的速度场。
正如前面一节提到的，Von Kármán的三层结构通用速度分布也适用于管内湍流，即：（4.2.6）但也存在以下缺点：>时，用上式计算管内湍流对流换热结果不满意，（1）当Pr30原因是完全忽略了粘性底层中的脉动（t ν＝0）；（2出的结果不为零，这不符合实际。
赖卡特（H.Reichardt ），对此进行了改进，提出了公式：（4.2.7） 由上式可以看出，当50y +≤时，t νν随y +减小而减小，在壁面处，t νν＝0（y +＝0）；在中心线处，w y r =将上式代入动量方程：(1)1t wdu y dy r νν+++++=−得（4.2.8）当0r =时，00r dudr ==。
最终可得无量纲通用速度分布：（4.2.9）工程上更多地直接采用尼古拉兹提出的速度分布。
尼古拉兹对36410Re 3.210×<<×范围内的管内湍流阻力与速度分布进行了广泛的实验研究，认为管内的湍流速度分布可表示为：（4.2.10） 其中，max u 是管中心线处速度，指数n 随Re 的变化（Re m u dν⋅=），如下表：施里希延（Schlichting.H.）推荐下面的速度分布式：（4.2.11）系数()c n 随n 的变化如下表:Re5105510× 61.310× 63.210×n78 9 10 ()c n8.749.7110.611.5普朗特基于通用速度分布，并综合实验数据修正，得出了通用的管内充分发展湍流阻力公式：（4.2.12） 上式称为光滑圆管的普朗特通用阻力公式，适用于6Re 3.410<×。
