反弯点法计算方法实例

《反弯点法》例题详解在数学中，反弯点法是一种求函数曲线的凹凸性质的方法。

通过求函数的导数和二阶导数，可以确定函数的凹凸区间和反弯点。

下面我们以一个例题来详细介绍反弯点法的具体步骤和求解过程。

例题：已知函数f(x) = x^3 - 3x^2 + 2x - 1，求函数的凹凸区间和反弯点。

步骤一：求函数的一阶导数f'(x)。

f'(x) = 3x^2 - 6x + 2步骤二：求函数的二阶导数f''(x)。

f''(x) = 6x - 6步骤三：求f''(x) = 0的解，即求二阶导数的零点。

6x - 6 = 0x = 1步骤四：求f''(x)在x < 1和x > 1两个区间的符号。

当x < 1时，取一个小于1的数代入f''(x)，比如x = 0，计算得f''(0) = -6，符号为负。

当x > 1时，取一个大于1的数代入f''(x)，比如x = 2，计算得f''(2) = 6，符号为正。

步骤五：根据f''(x)的符号确定函数的凹凸性质。

当f''(x) > 0时，函数在该区间上凹。

当f''(x) < 0时，函数在该区间上凸。

根据步骤四的计算结果，可以得出以下结论：当x < 1时，函数在该区间上凸。

当x > 1时，函数在该区间上凹。

步骤六：求函数的反弯点。

根据步骤三的计算结果，x = 1是函数的一个反弯点。

综上所述，函数f(x) = x^3 - 3x^2 + 2x - 1在x < 1时凸，在x > 1时凹，且有一个反弯点x = 1。

通过以上例题的详细解答，我们可以了解到反弯点法的求解过程和应用方法。

通过求函数的导数和二阶导数，我们可以确定函数的凹凸区间和反弯点，从而更好地理解和分析函数的性质。

水平荷载作用下采用反弯点法计算反弯点法是一种常用于计算水平荷载作用下的结构弯矩和剪力的方法。

在使用这种方法时，首先需要通过结构的截面特性和材料特性来确定结构的内力分布。

然后，通过计算不同截面的弯矩与剪力平衡点，找到结构的反弯点位置。

最后，通过分析反弯点处的内力分布，计算结构在水平荷载作用下的弯矩和剪力。

下面以梁为例，来介绍水平荷载作用下采用反弯点法计算的过程。

首先，给定一根梁的长度L和受力情况。

为了简化问题，我们假设梁的截面形状为矩形，截面高度为h，宽度为b，材料的弹性模量为E。

梁所受外力为均布荷载q。

接下来，我们根据梁的受力分析，计算出梁在距离x处的弯矩M和剪力V的分布式函数。

在这种情况下，由于梁是均布荷载作用的，所以梁上的弯矩和剪力都是连续变化的线性函数。

根据弯矩和剪力的定义，我们可以得到：M(x) = -qx^2/2 + C1x + C2V(x) = -qx + C1其中，C1和C2是根据边界条件得出的常数，用于确定梁的受力状态。

接下来，我们需要确定梁的反弯点位置。

反弯点是梁上由抗力导致的弯矩的变号点。

在这个点上，弯矩由正变为负，或由负变为正。

在反弯点附近，梁的内力状态发生了较大变化。

为了确定反弯点位置，我们可令M(x)=0，解得反弯点的位置为x=r。

将x=r代入V(x)的方程中，我们可以计算出反弯点处的剪力为V(r)=-qr+C1根据反弯点的定义，剪力也应该为零，因此可以得到C1=qr。

将C1=qr代入M(x)的方程中，我们可以计算出反弯点处的弯矩为M(r)=-qr^2/2+C2根据反弯点的定义，弯矩也应该为零，因此可以得到C2=qr^2/2最后，我们可以得到反弯点处的弯矩和剪力分布：M(r) = -qr^2/2 + qr^2/2 = 0V(r) = -qr + qr = 0这意味着在反弯点处，梁的弯矩和剪力都为零，这是一个特殊的位置。

通过计算反弯点的位置和反弯点处的内力分布，我们可以了解结构在水平荷载作用下的受力状态。

混凝土反弯点法计算题例题混凝土反弯点法是一种用于计算混凝土梁的强度和刚度的方法。

它基于混凝土在受拉应力作用下的裂缝性质，将混凝土截面分为受压区和受拉区。

在混凝土的受拉区出现第一根裂缝时，混凝土截面的强度随之降低，这个裂缝的位置就是梁的反弯点。

以下是一个混凝土反弯点法计算题的例题：【例题】一根混凝土矩形梁的截面宽度为b=200mm，高度为h=400mm，长度为L=4m。

梁的配筋已经确定，钢筋面积为As=2515mm2，混凝土强度等级为C30，梁的工作状态为常规状态。

使用混凝土反弯点法计算梁的极限承载力。

解题思路：1. 计算混凝土截面面积Ac和受拉区高度a。

$$Ac=bh=200mm\times400mm=80000mm^2$$根据混凝土抗拉强度σc和配筋率ρ，可以计算出混凝土受拉区高度a。

$$a=\frac{\sigma_c}{0.85f_y}\frac{1-\sqrt{1-2\rho}}{1.6}h$$其中，fy为钢筋的屈服强度，ρ为配筋率。

根据题目中的数据，可以计算出a的值为：$$a=\frac{2.6\times10^6Pa}{0.85\times300\times10^6Pa}\frac{1-\sqrt{1 -2\times\frac{2515mm^2}{200mm\times400mm}}}{1.6}\times400mm=7 7.57mm$$2. 计算混凝土受拉区的受拉力N和弯矩M。

根据梁的几何尺寸和工作状态，可以计算出梁上的荷载为：$$q=\frac{1.5kN}{m^2}$$其中，kN为单位长度的荷载。

因此，梁上的集中荷载为：$$P=qL=1.5kN/m^2\times4m=6kN$$根据静力平衡条件，可以计算出混凝土受拉区的受拉力N和弯矩M。

$$N=P=\frac{6kN}{2}=3kN$$$$M=\frac{PL}{4}=6kN\times4m/4=6kNm$$3. 计算混凝土受拉区的应力σ1和混凝土截面的极限承载力M1。

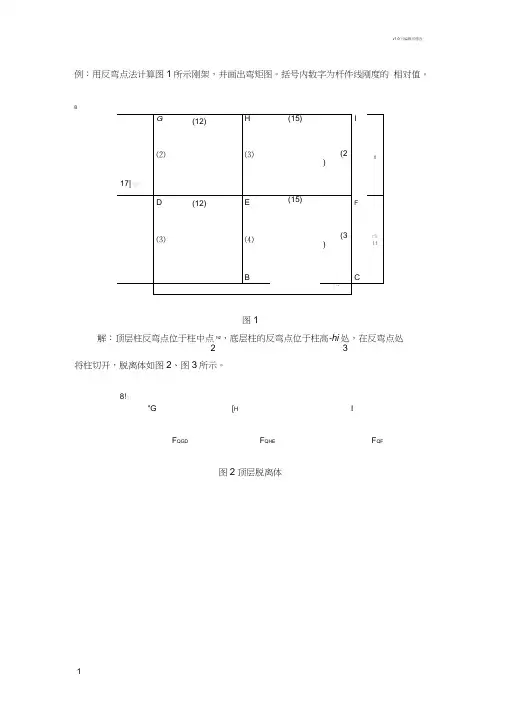
例：用反弯点法计算图1所示刚架，并画出弯矩图。

括号内数字为杆件线刚度的相对值。

8图1解：顶层柱反弯点位于柱中点h2，底层柱的反弯点位于柱高-hi处，在反弯点处2 3将柱切开，脱离体如图2、图3所示。

8!怡"G [H IF QGD F QHE F QF图2顶层脱离体图3底层隔离体顶层:底层:IFF QAD F QBE8IDA FC0.3 40.43 2 4(2)计算各柱剪力：EB0.286 8kN 2.29kNFQHE0.428 8kN 3.42kN FQADF QCF 0.3 25kN 7.5kN F QBE0.4 25kN10kN(3)计算杆端弯矩， 以节点E 为例说明杆端弯矩的计算F QIFF QGD杆端弯矩:M EHF QHEh 223.42kN ^^m 5.64 kN m （反弯点位于空处）2 2F QCF(1)求各柱剪力分配系数k k k k iGDIF-0.286 2 2 3 HE-0.428 3M EB F QBE匕 10kN 36 m 12 kN m3 32（反弯点位于柱汕处）计算梁端弯矩时, 先求出节点柱端弯矩之和为:M M EH EB17.64 kN m按梁刚度分配:12 M ED27 15M E F 刃17.64 17.64 图3是刚架弯矩图。

8i173.787.84 9.8 kN mkN m 3.783.783.133.7893.785.649.82・51 5.647.84123.7812.7812.781824图3弯矩图（单位kN m ）18。

反弯点法计算方法实例咱今儿就来唠唠这反弯点法计算方法实例。

嘿，你可别小瞧了它，这可是结构力学里挺重要的一块儿呢！比如说咱有个框架结构，就像搭起来的积木房子似的。

那这反弯点法呀，就是帮咱搞清楚这个“积木房子”受力之后会咋变形的。

咱先看看柱子，柱子上不是有好些个节点嘛，嘿，这节点可就有意思了，就像关节一样，能活动能弯曲。

那反弯点呢，就是柱子上那么一个特别的点，在这儿啊，柱子弯曲的方向会变。

咱来举个具体例子哈。

就说有个两层的框架，柱子啊梁啊都齐全。

那咱咋用反弯点法算呢？先找那些个关键的节点，看看它们的受力情况。

然后呢，根据一些个规则，确定反弯点的位置。

哎呀，你想想看，这就好比是走迷宫，得找到正确的路才能走出去。

咱找反弯点也是一样，得找对了，后面的计算才能顺顺利利的。

算的时候呢，要把柱子分成几段，每一段的内力都不一样。

这就好像切蛋糕，每一块的大小味道都有点不一样。

然后呢，根据反弯点的位置，算出每一段的弯矩呀剪力呀啥的。

这过程中可得细心点，别弄错了。

不然就像做饭放错调料一样，那味道可就不对啦！你说这反弯点法神奇不神奇？它能让咱清楚地知道这结构在受力的时候到底会怎么个变化法。

再比如说，要是这个框架受到了风的吹呀，或者别的啥外力，咱用反弯点法就能算出柱子和梁会怎么变形，会不会承受得住。

这就好像给这个“积木房子”做了个体检，看看它健不健康。

咱学这反弯点法，就像是掌握了一把钥匙，能打开结构力学里好多知识的大门呢！你要是学会了，那以后遇到啥结构问题，都能心里有底，知道该咋去分析解决。

反正我觉着吧，这反弯点法挺有用的，咱得好好学，好好研究。

别觉得它难就退缩了呀，多琢磨琢磨，多做做例子，肯定能搞明白的。

你说是不是？咱可不能被这点小困难给难住了呀，得勇往直前，把这知识给拿下！就这么干，准没错！。