结构力学中反弯点法计算例题2

《反弯点法》例题详解在数学中，反弯点法是一种求函数曲线的凹凸性质的方法。

通过求函数的导数和二阶导数，可以确定函数的凹凸区间和反弯点。

下面我们以一个例题来详细介绍反弯点法的具体步骤和求解过程。

例题：已知函数f(x) = x^3 - 3x^2 + 2x - 1，求函数的凹凸区间和反弯点。

步骤一：求函数的一阶导数f'(x)。

f'(x) = 3x^2 - 6x + 2步骤二：求函数的二阶导数f''(x)。

f''(x) = 6x - 6步骤三：求f''(x) = 0的解，即求二阶导数的零点。

6x - 6 = 0x = 1步骤四：求f''(x)在x < 1和x > 1两个区间的符号。

当x < 1时，取一个小于1的数代入f''(x)，比如x = 0，计算得f''(0) = -6，符号为负。

当x > 1时，取一个大于1的数代入f''(x)，比如x = 2，计算得f''(2) = 6，符号为正。

步骤五：根据f''(x)的符号确定函数的凹凸性质。

当f''(x) > 0时，函数在该区间上凹。

当f''(x) < 0时，函数在该区间上凸。

根据步骤四的计算结果，可以得出以下结论：当x < 1时，函数在该区间上凸。

当x > 1时，函数在该区间上凹。

步骤六：求函数的反弯点。

根据步骤三的计算结果，x = 1是函数的一个反弯点。

综上所述，函数f(x) = x^3 - 3x^2 + 2x - 1在x < 1时凸，在x > 1时凹，且有一个反弯点x = 1。

通过以上例题的详细解答，我们可以了解到反弯点法的求解过程和应用方法。

通过求函数的导数和二阶导数，我们可以确定函数的凹凸区间和反弯点，从而更好地理解和分析函数的性质。

混凝土反弯点法计算题例题混凝土反弯点法是一种用于计算混凝土梁的强度和刚度的方法。

它基于混凝土在受拉应力作用下的裂缝性质，将混凝土截面分为受压区和受拉区。

在混凝土的受拉区出现第一根裂缝时，混凝土截面的强度随之降低，这个裂缝的位置就是梁的反弯点。

以下是一个混凝土反弯点法计算题的例题：【例题】一根混凝土矩形梁的截面宽度为b=200mm，高度为h=400mm，长度为L=4m。

梁的配筋已经确定，钢筋面积为As=2515mm2，混凝土强度等级为C30，梁的工作状态为常规状态。

使用混凝土反弯点法计算梁的极限承载力。

解题思路：1. 计算混凝土截面面积Ac和受拉区高度a。

$$Ac=bh=200mm\times400mm=80000mm^2$$根据混凝土抗拉强度σc和配筋率ρ，可以计算出混凝土受拉区高度a。

$$a=\frac{\sigma_c}{0.85f_y}\frac{1-\sqrt{1-2\rho}}{1.6}h$$其中，fy为钢筋的屈服强度，ρ为配筋率。

根据题目中的数据，可以计算出a的值为：$$a=\frac{2.6\times10^6Pa}{0.85\times300\times10^6Pa}\frac{1-\sqrt{1 -2\times\frac{2515mm^2}{200mm\times400mm}}}{1.6}\times400mm=7 7.57mm$$2. 计算混凝土受拉区的受拉力N和弯矩M。

根据梁的几何尺寸和工作状态，可以计算出梁上的荷载为：$$q=\frac{1.5kN}{m^2}$$其中，kN为单位长度的荷载。

因此，梁上的集中荷载为：$$P=qL=1.5kN/m^2\times4m=6kN$$根据静力平衡条件，可以计算出混凝土受拉区的受拉力N和弯矩M。

$$N=P=\frac{6kN}{2}=3kN$$$$M=\frac{PL}{4}=6kN\times4m/4=6kNm$$3. 计算混凝土受拉区的应力σ1和混凝土截面的极限承载力M1。

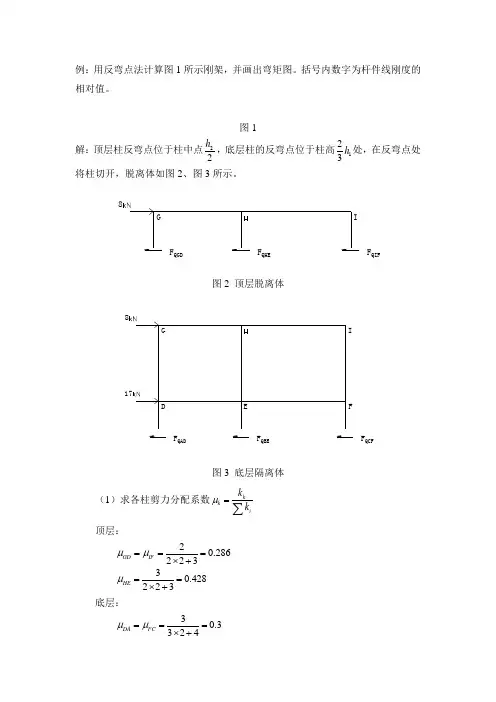
例：用反弯点法计算图1所示刚架，并画出弯矩图。

括号内数字为杆件线刚度的相对值。

图1解：顶层柱反弯点位于柱中点22h ，底层柱的反弯点位于柱高123h 处，在反弯点处将柱切开，脱离体如图2、图3所示。

F QIF图2 顶层脱离体F QAD F QBE F QCFGIFED817图3 底层隔离体（1）求各柱剪力分配系数kk ik k μ=∑ 顶层：20.286223GD IF μμ===⨯+30.428223HE μ==⨯+底层：30.3324DA FC μμ===⨯+40.4324EB μ==⨯+（2）计算各柱剪力：0.2868kN 2.29kN QGD QIF F F ==⨯= 0.4288kN 3.42kN QHE F =⨯= 0.325kN 7.5kN QAD QCF F F ==⨯= 0.425kN 10kN QBE F =⨯=（3）计算杆端弯矩，以节点E 为例说明杆端弯矩的计算 杆端弯矩：2 3.33.42kN 5.64kN m 22EH QHE h M F m =-⨯=-⨯=-⋅（反弯点位于22h 处）1 3.610kN 12kN m 33EB QBE h M F m =-⨯=-⨯=-⋅（反弯点位于柱123h 处） 计算梁端弯矩时，先求出节点柱端弯矩之和为：17.64kN m EH EB M M M =+=-⋅按梁刚度分配：1217.647.84kN m 27ED M =⨯=⋅ 1517.649.8kN m 27EFM =⨯=⋅ 图3是刚架弯矩图。

8 173.782.515.643.783.133.783.783.78912.785.649.87.841212.783.781824189图3 弯矩图（单位kN m）。

反弯点法计算方法实例反弯点法（BPM）是一种用于计算杆件等高耸结构的弯曲曲线和最大挠度的方法。

它被广泛运用于建筑和桥梁工程的设计和分析中。

本文将为您介绍反弯点法的计算方法，并提供一个实例来说明如何使用该方法。

反弯点法是一种基于弯矩的方法，它通过将结构模型离散为一系列杆件，并在节点处计算弯矩和反弯力，来确定结构的弯曲曲线。

通过计算结构中每个杆件的弯矩和反弯力，可以得到结构的整体弯曲曲线。

使用反弯点法计算结构的最大挠度时，可以在确定的点上计算出具有最大挠度的情况，从而更好地了解结构的性能。

接下来，我们将以一个悬臂梁为例，详细介绍反弯点法的计算步骤：1.构建模型：首先，我们需要根据实际情况绘制出悬臂梁的结构模型，并确定悬臂梁的几何形状、受力情况和材料性能参数等。

2.离散化：将悬臂梁离散为一系列杆件，并在节点处添加支座。

3.确定支反力：根据外部受力情况，可以计算出支座的反力。

在这个例子中，我们假设悬臂梁的一端受到水平荷载，并在另一端有一个固定支座。

因此，我们可以计算出固定支座的水平反力。

4.计算弯曲曲线：在每个节点处，根据杆件的长度、杨氏模量和截面惯性矩等参数，可以计算出弯矩和反弯力。

使用弯矩-转角关系式，可以计算出每个节点上的弯曲曲线。

5.确定反弯点：通过计算整个结构中的弯曲曲线，可以确定具有最大挠度的位置。

在这个例子中，我们将选取距离固定端0.3倍梁长的位置作为反弯点。

6.计算最大挠度：在选定的反弯点上，可以计算出具有最大挠度的情况，即该位置的挠度最大值。

7.结果分析：根据计算结果，可以进行结构的优化设计或评估。

在这个例子中，我们可以选择增加悬臂梁的截面尺寸或添加额外的支撑来减小最大挠度。

通过上述步骤，我们可以使用反弯点法计算出悬臂梁的弯曲曲线和最大挠度，并据此对结构进行进一步优化。

当然，这只是一个简单的例子，实际工程中可能涉及更复杂的结构和计算。

需要指出的是，反弯点法只是众多结构分析方法之一，它的适用范围和局限性需要结合具体情况来判断。

水平荷载作用下采用反弯点法计算反弯点法是结构力学中一种常用的计算方法，用于计算水平荷载作用下的结构变形和受力状态。

通过找出结构中的反弯点，即弯矩变化方向以及弯矩大小变化的位置，可以得到结构中各个截面的内力和变形情况。

本文将介绍反弯点法的基本原理和计算步骤，并用一个实例进行具体分析。

反弯点法的基本原理是假设结构在水平荷载作用下呈现弯矩分布曲线的形状是一条抛物线。

这条抛物线有一个最高点，称为反弯点。

利用这个假设，可以将结构截面沿着水平方向划分为两部分，即反弯点之前和反弯点之后。

反弯点之前的部分为正弯矩区域，反弯点之后的部分为负弯矩区域。

通过计算这两个区域的弯矩大小和位置，可以得到结构中各个截面的内力和变形。

对于一个梁的水平荷载作用下的反弯点法计算，具体步骤如下：1.画出结构的截面和荷载图，确定结构的几何形状和载荷情况。

2.假定结构的反弯点在梁的中点位置，即距离梁两端等分。

若已知反弯点的位置，可直接进行下一步骤的计算。

3.计算反弯点之前的正弯矩区域的弯矩大小和位置。

利用弯矩方程可以得到：M1 = (wl^2)/8其中，M1为反弯点之前的正弯矩，w为单位长度的均布荷载，l为梁的长度。

4.计算反弯点之后的负弯矩区域的弯矩大小和位置。

利用弯矩方程可以得到：M2 = (wl^2)/8其中，M2为反弯点之后的负弯矩。

5.通过计算得到的弯矩大小和位置，可以得到结构中各个截面的内力和变形。

根据梁的受力平衡条件，可以计算出梁的剪力和弯矩分布。

根据弹性力学理论，可以得到梁的挠度曲线和变形情况。

下面以一个简单的例子来说明反弯点法的具体应用。

假设有一根长度为6m的梁，受到均布荷载q=10kN/m作用。

我们要计算梁在水平荷载作用下的内力和变形情况。

首先，确定反弯点的位置。

由于荷载是均布荷载，梁的长度等分为两个部分，所以反弯点的位置在梁的中点，即3m处。

然后，计算反弯点之前的正弯矩区域的弯矩大小和位置。

根据反弯点法的计算公式，可以得到：M1=(q*l^2)/8=(10*3^2)/8=11.25kNm再计算反弯点之后的负弯矩区域的弯矩大小和位置，也得到：M2=(q*l^2)/8=(10*3^2)/8=11.25kNm最后，根据梁的受力平衡条件和弹性力学理论，可以计算出梁的剪力和弯矩分布，以及梁的挠度曲线和变形情况。

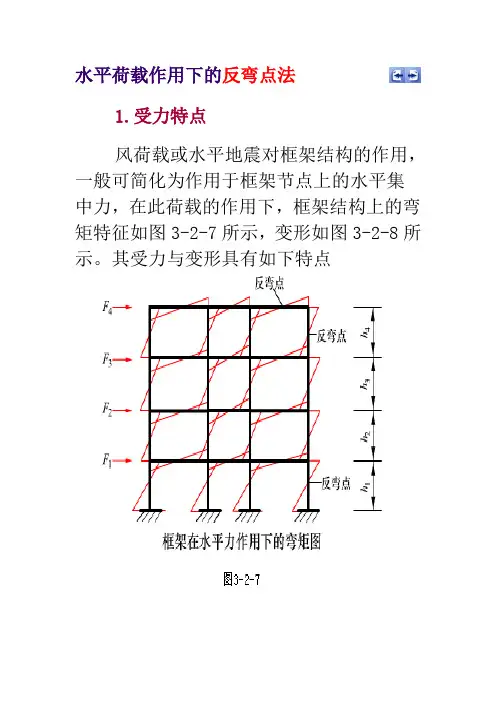
水平荷载作用下的反弯点法1.受力特点风荷载或水平地震对框架结构的作用，一般可简化为作用于框架节点上的水平集中力，在此荷载的作用下，框架结构上的弯矩特征如图3-2-7所示，变形如图3-2-8所示。

其受力与变形具有如下特点（1）各杆的弯矩为直线分布，且每个杆均有一个零弯矩点即反弯点；（2）在固定端处，角位移为零,但上部各层节点均有转角存在,节点的转角随梁柱线刚度比的增大而减小；（3）如忽略梁的轴向变形，同层内各节点具有相同的侧向位移，同层各柱具有相同的层间位移。

2.解题思路鉴于框架结构在水平荷载作用下具有上述受力变形特点，如能求出各柱的反弯点位置及反弯点处的剪力，就可以利用静力平衡条件求出各杆件的内力。

因此解题的关键是确定各柱反弯点的位置及反弯点处的剪力。

3.基本假定由受力特点可知，框架受力后节点会产生转角和侧移，但根据分析，当梁与柱的线刚度之比大于3时，节点转角很小，对内力影响不大，故可忽略即转角 =0（图3-2-9），实际上这等于是把框架梁简化为一刚性梁。

基本假定如下：（1）在求各柱子的剪力时，假定梁与柱的线刚度比为无穷大，即各节点转角为零；（2）在确定柱的反弯点位置时，假定除底层以外的其余各柱，受力后上下两端转角相同；(图3-2-10)（3）梁端弯矩可按梁的线刚度进行分配。

4.柱的反弯点高度——反弯点高度，指反弯点至柱下端的距离。

对于底层以上的各层柱，根据假定（2），各柱的上下端转角相等,则柱的上下端弯矩也应相同,所以反弯点在柱中部。

对于底层柱,当柱脚固定时,柱下端转角为零(图3-2-11(a))，上端转角为，因此柱上端弯矩比下端弯矩小,其反弯点则偏离柱中点而向上移,可取在层高处。

各柱反弯点的高度为：底层柱其余各柱5.各柱反弯点处的剪力设框架结构共有n层，每一层有m 个柱子，框架节点上作用有水平荷载、……，如图3-2-12(a)所示。

（1）第j层所受到的总剪力将框架沿第j层各柱的反弯点处切开，代以剪力和轴力，如图3-2-12(b)所示，本层总剪力为。

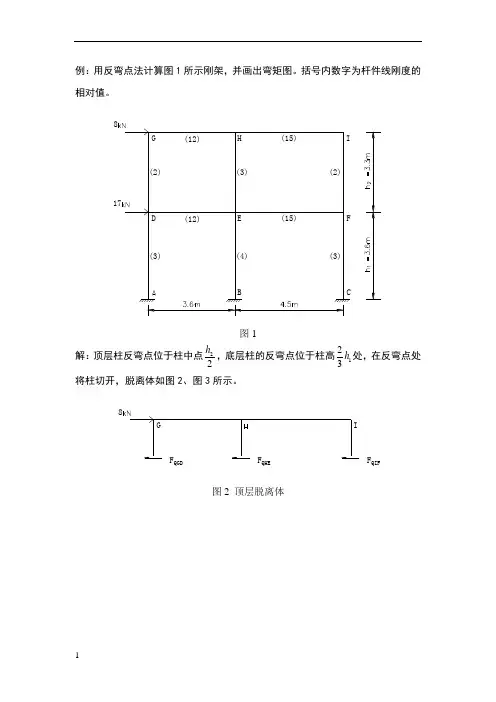
例：用反弯点法计算图1所示刚架，并画出弯矩图。

括号内数字为杆件线刚度的相对值。

图1解：顶层柱反弯点位于柱中点22h ，底层柱的反弯点位于柱高123h 处，在反弯点处将柱切开，脱离体如图2、图3所示。

F QIFQHE QGD图2 顶层脱离体F QAD F QBE F QCFGIFED817图3 底层隔离体（1）求各柱剪力分配系数kk ik k μ=∑ 顶层：20.286223GD IF μμ===⨯+30.428223HE μ==⨯+底层：30.3324DA FC μμ===⨯+40.4324EB μ==⨯+（2）计算各柱剪力：0.2868kN 2.29kN QGD QIF F F ==⨯= 0.4288kN 3.42kN QHE F =⨯= 0.325kN 7.5kN QAD QCF F F ==⨯= 0.425kN 10kN QBE F =⨯=（3）计算杆端弯矩，以节点E 为例说明杆端弯矩的计算 杆端弯矩：2 3.33.42kN 5.64kN m 22EH QHE h M F m =-⨯=-⨯=-⋅（反弯点位于22h 处）1 3.610kN 12kN m 33EB QBE h M F m =-⨯=-⨯=-⋅（反弯点位于柱123h 处） 计算梁端弯矩时，先求出节点柱端弯矩之和为：17.64kN m EH EB M M M =+=-⋅按梁刚度分配：1217.647.84kN m 27ED M =⨯=⋅ 1517.649.8kN m 27EFM =⨯=⋅ 图3是刚架弯矩图。

8173.782.51 5.643.783.133.783.783.78912.785.649.87.841212.783.781824189图3 弯矩图（单位kN m ⋅）。