第三章--位错理论

基于位错模型正演出地表的重力变化和重力梯度变化，是利用时变重力和梯度数据反演海底地震参数的基础。

在假定为各项同性的弹性半空间 （介质）中，设地下埋深 处有一点源(0，0， _3 )，如图2所示：()()()()()()()()()()21331133233333333333331233123233313313321;;2;;x R x G r G R R x R R R x x G r G R R x x R x r G R R x x r G Rερψερεεεεερψερεεψερεεψερ⎧⎡⎤+-⎪∆=--⎢⎥+-+-⎪⎢⎥⎣⎦⎪-⎪∆=-⎪⎨+-⎪∆''=-⎪+-⎪⎪⎪∆=⎩ (1.1)式中：R = ， ρ为介质密度，G 为牛顿引力常数有了点源位错的结果，就可以将其扩展为有限矩形断层震源计算。

位错的滑动矢量和其法矢量可以表示为：12312323(,,)(,cos sin ,sin cos )u u u u U U U U U δδδδ∆=∆∆∆=---(1.2)123(,,)(0,sin ,cos )n n n n δδ==--(1.3)然后对断层面进行积分，即：'''''120(,cos ,sin )LLij i j d d d x x u n δδξηψξηη∆---∆⎰⎰(1.4)最后结果用双竖线约定符号标示为简洁模式：1111(,)||(,)(,)(,)(,)f f p f p W f L p f L p W x x x x ξη=----+--(1.5)所以得引力位变化和重力变化的最后计算公式如下： 引力位变化：()()()()1233123(,,){[,,,],}||G S D T G C U U U U x x x ψρξηξηξηρξη∆=+++∆(1.6)22010(,)tan 2sec tan S R qI I ξηδδξδ=-++(1.7) 30210(,)tan 2sin [lg()2tan ]D R x q I I I ξηξδδξδ=---++(1.8)2230120(,)sin lg()2()(,)tan tan T R C x q I I I ξηξδδξδξη=-++++ (1.9)2(,)lg()lg()2C R R q I ξηξηηξ=-+-+-(1.10)式中：(,)lg()sin lg()R R d Iξηξδ=+-⋅+(1.11)11cos (1sin )()(,)()cos tan q R I δδηξηξδ--+++=(1.12)12(,)()tan R qI ξηξη-++= (1.13)R =(1.14) 23sin ()cos q d x x δδ=--(1.15) 03cos q q x δ=-(1.16)sin cos d q ηδδ=-(1.17)空间固定点的重力变化：()()()()()123312,{[,,,],}||g g g g g G G U S U U U C D T x x ρξηξηξηρξη∆=+++∆(1.18)参数，(,,,)ggggS CD T 是对(,,,)S D T C 进行微分到的，即 (,,,)(,,,)g g g g S D T C S C D T =Γ(1.19)3333(,,)|xq p q x x x η=Γ=∂∂∂∂∂---∂∂∂∂∂(1.20)具体的表达式为2sin cos (,)()g q q R R R S δδξηη=-++ (1.21)2(,)2sin ()g qdD I R R ξηδξ==-+(1.22)2cos (,)2cos ()()g q y q T I R R R R ξδξηδξη==++++(1.23)2(,)2cos sin lg()g R C I ξηδδξ==-+(1.24)cos sin y q ηδδ=+(1.25)这里G即为式1.18，f有数据反演的参数包括：倾角 ，长度L，宽度W，深度d，滑动角等。

金属位错理论位错的概念最早是在研究晶体滑移过程时提出来的。

当金属晶体受力发生塑性变形时，一般是通过滑移过程进行的，即晶体中相邻两部分在切应力作用下沿着一定的晶面晶向相对滑动，滑移的结果在晶体表面上出现明显的滑移痕迹——滑移线。

为了解释此现象，根据刚性相对滑动模型，对晶体的理论抗剪强度进行了理论计算，所估算出的使完整晶体产生塑性变形所需的临界切应力约等于G/30，其中G为切变模量。

但是，由实验测得的实际晶体的屈服强度要比这个理论值低3~4数量级。

为解释这个差异，1934年，Taylor，Orowan和Polanyi 几乎同时提出了晶体中位错的概念，他们认为：晶体实际滑移过程并不是滑移面两边的所有原子都同时做刚性滑动，而是通过在晶体存在着的称为位错的线缺陷来进行的，位错再较低应力的作用下就能开始移动，使滑移区逐渐扩大，直至整个滑移面上的原子都先后发生相对滑移。

按照这一模型进行理论计算，其理论屈服强度比较接近于实验值。

在此基础上，位错理论也有了很大发展，直至20世纪50年代后，随着电子显微镜分析技术的发展，位错模型才为实验所证实，位错理论也有了进一步的发展。

目前，位错理论不仅成为研究晶体力学性能的基础理论，而且还广泛地被用来研究固态相变，晶体的光、电、声、磁和热学性，以及催化和表面性质等。

一、位错的基本类型和特征位错指晶体中某处一列或若干列原子有规律的错排，是晶体原子排列的一种特殊组态。

从位错的几何结构来看，可将他们分为两种基本类型，即刃型位错和螺型位错。

1、刃型位错刃型位错的结构如图1.1所示。

设含位错的晶体为简单立方晶体，晶体在大于屈服值的切应力 作用下，以ABCD面为滑移面发生滑移。

多余的半排原子面EFGH犹如一把刀的刀刃插入晶体中，使ABCD 面上下两部分晶体之间产生了原子错排，故称“刃型位错”。

晶体已滑移部分和未滑移部分的交线EF就称作刃型位错线。

图1.1 含有刃型位错的晶体结构刃型位错结构的特点：（1）刃型位错有一个额外的半原字面。

材料科学基础位错理论位错理论是材料科学领域中的重要概念之一、它是位错理论与晶体缺陷之间相互关联的核心。

本文将从位错的定义、分类和特征出发，进一步介绍位错理论的基本原理和应用。

首先，位错是固体晶体结构中的一种缺陷。

当晶体晶格中发生断裂、错位或移动时，就会形成位错。

位错可以被看作是晶体中原子排列的异常，它具有一定的形态、构型和特征。

根据位错发生的方向和类型，位错可分为直线位错、面位错和体位错。

直线位错是沿晶体其中一方向上的错排，常用符号表示为b。

直线位错一般由滑移面和滑移方向两个参数来表征。

滑移面是指位错的平移面，滑移方向是位错在晶体中的移动方向。

直线位错可以进一步分为边位错和螺位错。

边位错的滑移面为滑移方向的垂直面，螺位错则是在滑移面上存在沿位错线方向扭曲的位错。

面位错是晶体晶格上的一次干涉现象，即滑移面上的两部分之间发生错排。

面位错通常由面位错面和偏移量来描述。

面位错可以是平面GLIDE面位错、垂直GLIDE面位错或螺脚面位错。

体位错是沿体方向上的排列不规则导致的位错。

体位错通常是由滑移面间的晶体滑移产生的。

位错理论的基本原理是通过研究位错在晶体中的移动机制和相互作用，来理解材料的塑性变形和力学行为。

位错理论最早由奥斯勒(Oliver)于1905年提出，他认为材料的塑性变形是由于位错在晶体中游走和相互作用所引起的。

这一理论为后来的位错理论奠定了基础。

位错理论的应用非常广泛。

在材料加工和设计中，位错理论被广泛用于控制材料的力学性能和微观结构。

通过控制位错的生成、运动和相互作用，可以获得理想的材料性能。

同时，位错理论也被用于研究材料的磁性、电子输运和热传导性能等方面。

此外，位错理论也在材料的缺陷工程和腐蚀研究中发挥着重要作用。

通过控制位错的形态和分布，在材料中引入有利于抵抗腐蚀的位错类型，可以提高材料的抗腐蚀性能。

位错理论也可以用于解释材料的断裂行为和疲劳寿命等方面。

总结起来，位错理论是材料科学基础中的重要内容。

位错理论铝合⾦⽣产中的冷热变形微观组织绪论：铝及铝合⾦在实际⽣产中，主要以挤压形式进⾏⽣产，随着加⼯⼯艺和⽣产技术得到飞速发展，⼈们对铝及铝合⾦轧板的要求⽇益增多。

对于变形铝合⾦来说，由于所含的合⾦元素不同，需要不同的变形⽅式：冷变形和热变形。

这⾥简单介绍在这两种变形的微观组织。

关键词：铝及铝合⾦，变形铝合⾦，冷变形和热变性。

⽬录铝合⾦⽣产中的冷热变形微观组织 (1)绪论 (1)⼀、冷变形中铝合⾦微观组织 (3)1.1亚结构 (3)1 .2变形织构 (3)⼆、热变形中的纤维组织 (5)2.1铝合⾦热变形中的动态回复 (5)2.2铝合⾦热变形中的再结晶 (6)三、铝合⾦变形微结构的分类 (6)参考⽂献 (8)⼀、冷变形中铝合⾦微观组织铝材冷加⼯后，随着外形的改变．晶粒皆沿最⼤主变形发展⽅向被拉长、拉细或压扁。

冷变形程度越⼤，品粒形状变化也越⼤。

在晶粒被拉长的同时，晶间的夹杂物也跟着拉长，使冷变形后的⾦属出现纤维组织。

1.1亚结构亚结构包括两种类型：较低温度下产⽣的胞状结构以及变形后因回复形成的亚晶[1]。

⾦属晶体经过较⼤的冷塑性变形后，由于位错密度增⼤和发⽣交互作⽤，⼤量的位错堆积在局部区域，并相互缠结形成不均匀的分布，在晶粒内部出现了许多取向不同、⼤⼩约为10-3～10-6cm 的⼩晶块，这些⼩晶块(或⼩晶粒间)的取向差不⼤(⼩于1°)，所以它们仍然维持在同⼀个⼤晶粒范围内，这些⼩晶块称为亚晶[2]，这种组织称为亚结构。

在冷轧变形中，随着应变量的增加，晶粒发⽣分裂，内部就⽣成亚结构[3]。

亚晶的⼤⼩、完整程度、取向差与材料的纯度及形量和变形温度有关。

当材料中含有杂质和第⼆相时，在变形量⼤和变形温度低的情况下，所形成的亚晶⼩，亚晶间的取向差⼤，亚晶的完整性差(即亚晶内晶格的畸变⼤)。

冷变形过程中，亚晶结构对⾦属的加⼯硬化起重要作⽤，由于各晶块的⽅位个同，其边界⼜为⼤量位错缠结，对晶内的进⼀步滑移起阻碍作⽤。

一、影响扩散系数的因素有哪些？1、温度：温度越高，扩散越快2、晶体结构：结构不同，扩散系数不同3、固溶体类型：不同类型的固溶体，溶质原子扩散激活能不同，间隙原子扩散激活能比置换原子的小所以扩散速度比较快4、晶体缺陷：晶界，位错，空位都会对扩散产生影响。

5、固体浓度：浓度越大，扩散越容易二、什么是柯肯达尔效应，如何解释柯肯达尔效应。

（1）由置换互溶原子因相对扩散速度不同而引起标记移动的不均衡现象称为柯肯达尔效应。

（2）把Cu ，Ni 两金属对焊在一起，并在焊接面钨丝作为晶界标志，加热且长时间保温后，晶界向Ni 一侧移动了一段距离，表明Ni 向Cu 一侧扩散过来的原子数目比Cu 向Ni 一侧扩散过来的原子数目多，过剩的Ni 原子使Cu 侧发生点阵膨胀，而Ni 侧原子减少的地方发生点阵收缩导致界面向Ni 一侧漂移，这就是柯肯达尔效应三、若已知跳跃频率为ν，晶格常数为a ，求简单立方晶格金属和面心立方晶格金属的自扩散系数。

设浓度分别为C 1和C 2，扩散的单位间距为α则面密度为n 1=C 1α n 2=C 2α扩散通量为()dx dC k dx dC k C C k n k n k J 22121ναανανανν-=⎪⎭⎫ ⎝⎛-∙=-=-= 其中k 为原子跳过扩散面的概率又根据菲克第一定律：J=-D dxdC ,则2ναk D = 在简单立方晶格中，k=1/6，a =α，所以D=1/62a ν在面心立方晶格中，k=1/4，a 33=α，所以D=1/122a ν 四、位错反应的条件是什么，面心立方晶格金属中[][]a a a 110211121266-⎡⎤→+⎢⎥⎣⎦能否进行？ 1，几何条件：根据柏氏矢量b r 守恒性，反应后诸位错的柏氏矢量k b 之和应等于反应前诸位错 的柏氏矢量i b 之和 即 k b ∑=ib ∑ 能量条件：位错反应必须是一个伴随着能量降低的过程即反应后各位错能量之和小于反应 前各位错能量之和，由于位错能量正比于其柏氏矢量的平方故2i b ∑>2k b ∑2，几何条件a a a 1=21266⨯⨯+⨯ a a a 1=12266⨯⨯+⨯ a a a 0=11266⨯⨯-⨯从几何条件看b r =1b r +2b r 满足，从能量条件看2a 2>2a 6+2a 6=2a 3。

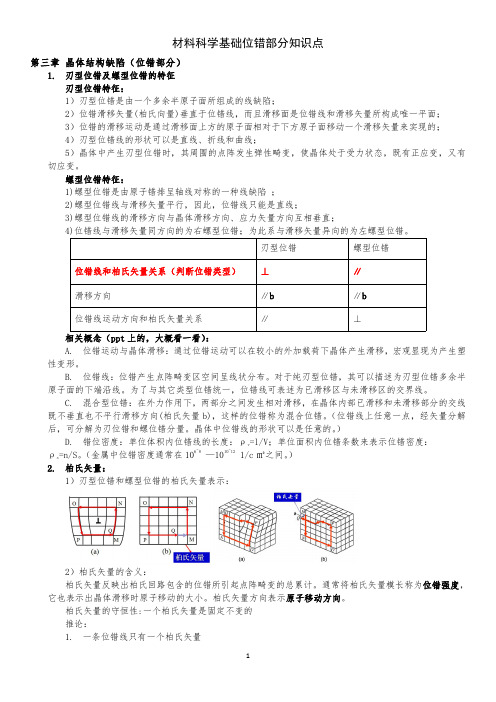
材料科学基础位错部分知识点第三章晶体结构缺陷（位错部分）1.刃型位错及螺型位错的特征刃型位错特征：1）刃型位错是由一个多余半原子面所组成的线缺陷；2）位错滑移矢量(柏氏向量)垂直于位错线，而且滑移面是位错线和滑移矢量所构成唯一平面；3）位错的滑移运动是通过滑移面上方的原子面相对于下方原子面移动一个滑移矢量来实现的；4）刃型位错线的形状可以是直线、折线和曲线；5）晶体中产生刃型位错时，其周围的点阵发生弹性畸变，使晶体处于受力状态，既有正应变，又有切应变。

螺型位错特征：1)螺型位错是由原子错排呈轴线对称的一种线缺陷；2)螺型位错线与滑移矢量平行，因此，位错线只能是直线；3)螺型位错线的滑移方向与晶体滑移方向、应力矢量方向互相垂直；4)位错线与滑移矢量同方向的为右螺型位错；为此系与滑移矢量异向的为左螺型位错。

刃型位错螺型位错位错线和柏氏矢量关系（判断位错类型）⊥∥滑移方向∥b∥b位错线运动方向和柏氏矢量关系∥⊥相关概念（ppt上的，大概看一看）：A.位错运动与晶体滑移：通过位错运动可以在较小的外加载荷下晶体产生滑移，宏观显现为产生塑性变形。

B.位错线：位错产生点阵畸变区空间呈线状分布。

对于纯刃型位错，其可以描述为刃型位错多余半原子面的下端沿线。

为了与其它类型位错统一，位错线可表述为已滑移区与未滑移区的交界线。

C.混合型位错：在外力作用下，两部分之间发生相对滑移，在晶体内部已滑移和未滑移部分的交线既不垂直也不平行滑移方向(柏氏矢量b)，这样的位错称为混合位错。

（位错线上任意一点，经矢量分解后，可分解为刃位错和螺位错分量。

晶体中位错线的形状可以是任意的。

）=l/V；单位面积内位错条数来表示位错密度：D.错位密度：单位体积内位错线的长度：ρv=n/S。

（金属中位错密度通常在106~8—1010~121/c㎡之间。

）ρs2.柏氏矢量：1）刃型位错和螺型位错的柏氏矢量表示：2）柏氏矢量的含义：柏氏矢量反映出柏氏回路包含的位错所引起点阵畸变的总累计。