小学四年级奥数专项练习(八)数线段与长方形

四年级奥数思维训练专题-数数图形专题简析：当线段、角、三角形、长方形等图形重重叠叠地交错在一起时就构成了复杂的几何图形.要想准确地计数这类图形中所包含的某一种基本图形的个数，必须注意以下几点：1，弄清被数图形的特征和变化规律.2，要按一定的顺序数，做到不重复，不遗漏.例1：数一数下图中共有多少个三角形.分析：以AD上的线段为底边的三角形也是1+2+3=6个；以EF上的线段为底边的三角形也是1+2+3=6个.所以图中共有6×2=12个三角形.试一试1：数一数下面各图中各有多少个三角形.（）个三角形（）个三角形例2：数一数下图中有多少个长方形.·分析：数长方形与数线段的方法类似.可以这样思考，图中的长方形的个数取决于AB或CD边上的线段，AB边上的线段条数是1+2+3=6条，所以图中有6个长方形.试一试2：数一数下面各图中分别有多少个长方形.（）个长方形数数图形（二）专题简析：“数图形”时，既可以逐个计数，也可以把图形分成若干个部分，先对每部分按照各自构成的规律数出图形的个数，再把他们的个数合起来.例1：数一数下图中有多少个长方形？分析：AB边上有线段1+2+3=6条，把AB边上的每一条线段作为长，AD边上的每一条线段作为宽，每一个长配一个宽，就组成一个长方形，所以，图中共有6×3=18个长方形.即：长边线段数×宽边线段数=长方形的个数试一试1：数一数，下图中有( )个长方形.例2：数一数，下图中有多少个正方形？（每个小方格是边长为1的正方形）分析：图中边长为1个长度单位的正方形有3×3=9个，边长为2个长度单位的正方形有2×2=4个，边长为3个长度单位的正方形有1×1=1个.所以图中的正方形总数为：1+4+9=14个.经进一步分析可以发现，由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为：1×1＋2×2＋…＋n×n.试一试2：数一数下图中有（）个正方形.（每个小方格为边长是1的小正方形）例3：数一数右图中有多少个正方形？(其中每个小方格都是边长为1个长度单位的正方形)分析：边长是1个长度单位的正方形有6×4=24个；边长是2个长度单位的正方形有（6－1）×（4－1）=15个；边长是3个长度单位的正方形有（6－2）×（4－2）=8个；边长是4个长度单位的正方形有（6－3）×（4－3）=3个；共有：24＋15＋8＋3=50个.如果一个长方形的长被分成m等份，宽被分成n等份（长和宽的每一份都是相等的）那么正方形的总数为：mn+(m－1)(n－1)＋(m －2)(n－2)＋…＋(m－n＋1)·1试一试3：数一数下图中有( )个正方形.。

四年级数学线段练习题库一、线段的长度计算1. 计算以下线段的长度：(1) AB，其中A(-2, 3)，B(4, 1)。

(2) CD，其中C(5, -2)，D(1, 5)。

(3) EF，其中E(-3, -4)，F(-6, -1)。

(4) GH，其中G(0, 0)，H(3, 4)。

二、线段的比较2. 比较下列线段的长度，写出符号"<"、">"或"="。

(1) AB和CD，其中A(-1, 2)，B(3, 4)，C(0, 1)，D(2, 3)。

(2) EF和GH，其中E(2, 4)，F(7, 1)，G(1, 3)，H(6, 2)。

(3) IJ和KL，其中I(-2, -5)，J(3, -1)，K(-1, -3)，L(4, -1)。

三、线段的延长与缩短3. 延长或缩短下列线段，使其长和原线段长度的比例为：(1) PQ，比例为1：2，其中P(-3, 4)，Q(2, 1)。

(2) RS，比例为3：2，其中R(1, -3)，S(4, 2)。

(3) TU，比例为1：3，其中T(-4, -2)，U(3, 1)。

四、线段的垂直与平行4. 判断下列线段是否垂直或平行：(1) VW和XY，其中V(-2, 1)，W(3, 4)，X(-1, -2)，Y(4, -1)。

(2) ZA和BC，其中Z(-3, 4)，A(1, 2)，B(5, 6)，C(7, 3)。

(3) DE和FG，其中D(2, 1)，E(4, 5)，F(0, 3)，G(2, 7)。

五、线段的位置关系5. 判断下列线段的位置关系，写出"相交"、"平行"或"相交于一点"。

(1) JK和LM，其中J(1, 4)，K(5, 1)，L(2, 2)，M(3, -1)。

(2) NO和PQ，其中N(-2, 1)，O(3, -2)，P(-1, 0)，Q(2, -3)。

小学四年级数学练习题画线段在小学四年级的数学学习中，画线段是一项基础而重要的技能。

通过画线段，孩子们可以更好地理解和运用数学知识。

本文将介绍一些小学四年级的数学练习题，并展示如何画出所给线段。

练习题一：长短不一的线段1. 请通过画线段的形式，将下列线段按照长度从短到长排列：a) 3 cm b) 8 cm c) 5 cm d) 2 cm参考答案：d) 2 cm a) 3 cm c) 5 cm b) 8 cm2. 将下列数字和长度相匹配，然后画出相应的线段：a) 4 cm b) 7 cm c) 9 cm d) 6 cm参考答案：a) 4 cm 对应的线段 b) 7 cm 对应的线段 c) 9 cm 对应的线段 d) 6 cm 对应的线段练习题二：根据题目要求画线段1. 在操场的一个边长为20米的正方形跑道上，甲乙两人同时开始跑步，没跑一圈，甲比乙多跑4米。

请画出甲乙两人第一次相遇时的线段。

参考答案：在跑道的某一点，画出甲与乙的相遇点，线段的长度为4米。

2. 请先画一个3厘米的线段AB，再向右平移5厘米，得到线段CD。

请画出线段CD。

参考答案：在线段AB的右侧画一条与AB平行的线段，长度为5厘米，得到线段CD。

练习题三：用尺子度量线段1. 用尺子来度量下列线段的长度，并写出相应的长度：a) 6 cm b) 9 cm c) 12 cm d) 3 cm参考答案：a) 6 cm 长度的线段 b) 9 cm 长度的线段 c) 12 cm 长度的线段 d) 3 cm 长度的线段2. 从A点到B点的距离为10厘米，请用尺子度量出这段距离，并在纸上画出这个线段。

参考答案：在纸上画出长度为10厘米的线段，代表从A点到B点的距离。

通过这些练习题，孩子们可以锻炼自己的线段画画技巧，培养准确的度量和判断能力。

同时，也有助于加深对数学概念的理解，提高数学解题的能力。

在画线段时，孩子们需要注意以下几点：1. 使用标尺或尺子来测量线段的长度，并以准确的长度画出线段。

几何计数知识结构一、公式计算法几何计数内容很广，包括数线段的条数，角的个数，长方形、正方形、三角形、平行四边形、梯形等图形的个数，也包括数立体图形的个数。

图形的计数一般有两种思考方法：公式计算法和分类计数法。

三年级学习的线段、长方形和正方形的计数就属于公式计算法。

（1）一条线段有两个端点，若这条线段上有n个点，那么线段总数是（n－1）＋（n＋2）＋…＋3＋2＋1（2）如果一个长方形的长边上有n个小格，宽边上有m个小格，那么长方形的总数是（1＋2＋3＋…＋n）×（1＋2＋…＋m）（3）如果把正方形各边都n等分，那么正方形的总数是n2＋（n－1）2＋（n－2）2＋…＋32＋22＋12上面计算线数的方法也可用于计算角的个数，而且，根据这些计数方法在以后还可以类推出立体图形的计算方法。

二、对应法将难以计数的数量与某种可计量的事物联系起来，只要能建立一一对应的关系，那么这两种事物在数量上是相同的．事实上插入法和插板法都是对应法的一种表现形式．重难点（1）分类数图形。

（2）对应法数图形。

例题精讲一、分类数图形【例 1】下图的两个图形（实线）是分别用10根和16根单位长的小棍围成的．如果按此规律（每一层比上面一层多摆出两个小正方形）围成的图形共用了60多根小棍，那么围成的图形有几层，共用了多少根小棍？【巩固】如图所示，用长短相同的火柴棍摆成3×1996的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍?【例 2】图中有______个正方形．【巩固】数一数：图中共有________ 个正方形。

【例 3】 右图中三角形共有 个．【巩固】 数一数图中有_______个三角形．【例 4】 图中共有多少个三角形？CB A【巩固】 下图是由边长为1的小三角形拼成，其中边长为4的三角形有_____个。

【例 5】 如图，每个小正方形的面积都是l 平方厘米。

则在此图中最多可以画出__________个面积是4平方厘米的格点正方形(顶点都在图中交叉点上的正方形)。

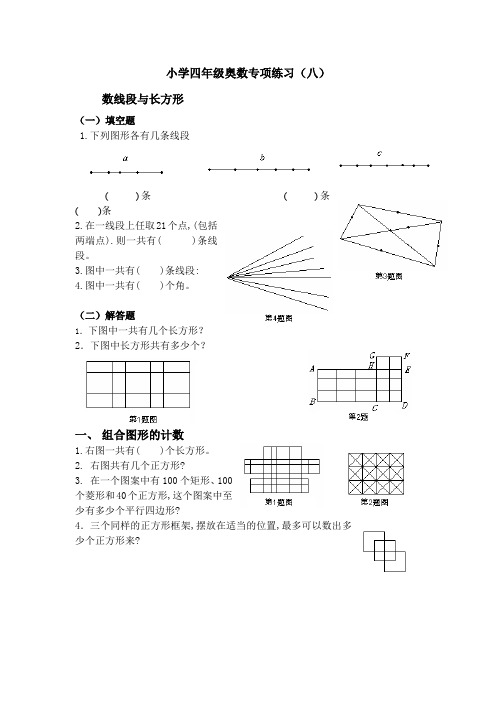
小学四年级奥数专项练习（八）数线段与长方形（一）填空题1.下列图形各有几条线段( )条( )条( )条2.在一线段上任取21个点,(包括两端点).则一共有( )条线段。

3.图中一共有( )条线段:4.图中一共有( )个角。

（二）解答题1．下图中一共有几个长方形？2．下图中长方形共有多少个？一、组合图形的计数1.右图一共有( )个长方形。

2. 右图共有几个正方形?3. 在一个图案中有100个矩形、100个菱形和40个正方形,这个图案中至少有多少个平行四边形?4．三个同样的正方形框架,摆放在适当的位置,最多可以数出多少个正方形来?数线段与长方形（一）填空题1.下列图形各有几条线段( )条( )条( )条答案：a有10条, b有15条, c有21条。

解析：a中以第一个端点为起点的线段有4条；以第二个端点为起点的线段有3条；以第三个端点为起点的线段有2条；以第四个端点为起点的线段有1条。

所以一共有：4+3+2+4=10条线段。

同理得出b中的线段有15条；c中的线段有21条。

2.在一线段上任取21个点,(包括两端点).则一共有( )条线段。

答案：(1+2+3+4+……+19+20)=(20+1)⨯20÷2=210(条)。

解析：点金术:如果线段上的基本线段有n条,则总的线段数为: 1+2+3+4+……+nn)1(2。

+n(=÷n+-)1⨯3.下图一共有( )条线段:答案：(1+2)⨯4+(3+2+1)⨯2=12+12=24(条)。

解析：如果图形比较复杂时,可以先找出线段条数相等的线段,再加起来。

4.下列图形中,一共有( )个角。

答案：6+5+4+3+2+1=21(个)。

解析：如果一个角内一共有几个基本角，则总的角(锐角)一共有：n)1(2。

+n⨯÷（二）解答题1.下图中一共有几个长方形？答案：(5+4+3+2+1)⨯(3+2+1)=(6⨯5÷2)⨯(4⨯3÷2)=15⨯6=90(个)。

小学生奥数几何题、计算题、计数练习题1.小学生奥数几何题练习题1、一个长方体的长、宽、高分别是11厘米、6厘米、4厘米，如果高增加3厘米，表面积增加多少平方厘米？2、一个正方体木块，表面积是30平方分米，如果把它据成大小一样的8个小正方体木块，每个小木块的表面积是多少？3、一块长方体石料，长4分米，横截面是一个边长为0.5分米的正方形，这块石料的表面积是多少？如果每立方分米石料重2.7千克，这块石料有多重？4、长方体的右侧面面积是12平方厘米，前面面积是8平方厘米，上面面积是6平方厘米，这个长方体的体积是多少立方厘米？5、把一个体积为460立方厘米的石块放入一个长方体容器中，完全进入水中后，水面由148厘米上升到150厘米，这个容器的底面积是多少？2.小学生奥数计算题练习题计算题：1、用竖式计算.18.25×34=2、用竖式计算.9.35×4.2=3、用竖式计算.15.07×9.8=4、用竖式计算.7.02×0.56=(得数保留两位小数)5、81.25×0.6×9.3=6、15×3.6+4.83=7、98.42×2.5-83.7=8、700×0.34×2=9、172.4×6.2+2724×0.38=10、4.75-9.64+8.25-1.36=11、3.17-2.74+4.7+5.29-0.26+6.3=12、(5.25+0.125+5.75)×8=13、34.5×8.23-34.5+2.77×34.5=14、6.25×0.16+264×0.0625+5.2×6.25+0.625×20=15、0.035×935+0.035+3×0.035+0.07×61×0.5=3.小学生奥数计算题练习题1、16+815+328-235-7442、456797+455457796+1153、(13+25+37+49)(113+135+157+179)4、2005200612004+122003200320055、(1996+19199696+191919969696)19191919969696966、(1+0.12+0.23)(0.12+0.23+0.34)-(1+0.12+0.23+0.34)(0.12+0.23)7、1+312+516+7112+9120+11130+13142+15156+17172+191908、325+358+3811++31972009、112+224+347+4711+51116+6162210、12+56+1112+1920+2930+4142+97019702+9899990011、123+246+369++100200300234+468+6912++20030040012、127+1712+11217+11722++19297+1971024.小学生奥数计数练习题1、把一包糖果分给小朋友们，如果每人分10粒，正好分完；如果每人分16粒，则3人分不到，这包糖有_________粒。

四年级数学线段的练习题1. 小明有一个10厘米长的线段，他想将它平均分成4段，每段的长度相等。

请问每段线段的长度是多少？2. 小红有一条线段，长度是18厘米。

她将这条线段分成3段，其中两段的长度分别是6厘米和8厘米，那么第三段线段的长度是多少？3. 在一张纸上，小明画了一条线段AB，长度为16厘米。

他又在这条线段上确定了一个点C，使得AC的长度是8厘米。

请问BC的长度是多少？4. 小华有一段线段，长度是24厘米。

他将这段线段分成4段，其中三段的长度分别是4厘米、6厘米和8厘米，那么第四段线段的长度是多少？5. 小明在纸上画了一条线段，长度是15厘米。

他突然想将这条线段分成3段，其中两段的长度分别是5厘米和7厘米，那么第三段线段的长度是多少？6. 小红有一段线段，长度是27厘米。

她将这段线段分成9段，每段的长度相等，那么每段线段的长度是多少？7. 小华在画纸上画了一个5厘米长的线段AB，又在这条线段上确定了一个点C，使得AC的长度是2厘米。

请问BC的长度是多少？8. 小明有一段线段，长度是30厘米。

他将这段线段分成5段，其中四段的长度分别是6厘米、8厘米、10厘米，那么第五段线段的长度是多少？9. 小红在纸上画了一条线段，长度是21厘米。

她想将这条线段分成3段，其中两段的长度分别是7厘米和10厘米，那么第三段线段的长度是多少？10. 小华有一段线段，长度是42厘米。

他将这段线段分成6段，每段的长度相等，那么每段线段的长度是多少？以上是四年级数学线段的练习题，希望能帮助你巩固线段的相关知识。

四年级线段图练习题线段图是图示统计数据的一种方式，通过线段的长短来表示不同数量或比例的数据。

在四年级数学中，线段图常用来解决一些实际问题，帮助我们更好地理解数据的分布。

接下来，我们将通过一些练习题来巩固和提升我们对线段图的理解和应用。

练习题1：下图是小明一周每天上学所花时间的线段图，请根据图中信息回答以下问题：1. 小明一周上学所花的总时间是多少？2. 周三上学的时间和周五上学的时间之间相差多少分钟？3. 哪天上学时间最长，上学时间是多少分钟？4. 周二上学的时间和周四上学的时间加起来是多少分钟？练习题2：下图是小华一周每天学习不同科目所花时间的线段图，请根据图中信息回答以下问题：1. 小华一周学习的总时间是多少分钟？2. 哪一天学习英语的时间最短，学习时间是多少分钟？3. 周三学习的总时间和周五学习的总时间之间相差多少分钟？4. 数学和科学两门学科的总学习时间是多少分钟？练习题3：下图是小杰一周每天跑步的距离线段图，请根据图中信息回答以下问题：1. 小杰一周跑步的总距离是多少米？2. 周三和周五跑步的距离之差是多少米？3. 哪一天跑步距离最多，跑了多少米？4. 周二和周四跑步的距离加起来是多少米？练习题4：小明、小华和小杰一周每天阅读的时间线段图如下图所示，请根据图中信息回答以下问题：1. 三人一周阅读的总时间是多少分钟？2. 哪个孩子一周阅读的总时间最长，阅读的时间是多少分钟？3. 哪一天三人阅读的总时间最短，总时间是多少分钟？4. 哪一天小明和小杰阅读的总时间比小华多，差多少分钟？通过以上练习题，我们可以加深对线段图表示数据的理解和分析能力。

希望通过不断的练习和探索，大家能够更加熟练地运用线段图解决实际问题，并且在数学学习中取得更好的成绩！。

2019年四年级数学奥数练习10数线段与长方形习题（B)一、填空题:1.数一数以下图共有( ) 条线段.( ) 条. ( ) 条.2.数一数以下图共有( ) 条线段.( ) 条. ( ) 条.3.以下图中各有几个三角形:③4.以下图中各有（）个三角形.以下图中有()个长方形.D CA B6.数一数以下图有（）个长方形.D C）个长方形.7.以下图共有（D A C BA B数一数图中长方形的个数.D CA B9.数一数下边各图有多少个长方形.(a)(b)以下图中一共有几个长方形?二、解答题:数一数下边各图有多少个正方形？a b2.以下图有多少个正方形 ?多少个长方形?3.以下图中各有多少个正方形?3.a b4.a5.以下图有多少个长方形?6.7.8.9.10.11.12.13.14.15.16.17.18.———————————————答案——————————————————————19.20.一、填空题:21.16;30.22.23.36;27.24.25.①18;②27;③20.26.27.①33;②24.28.29.10个.图中长方形的个数与因此长方形的个数等于AB AB边上所分红的线段的条数相关边上线段的条数,即长方形个数为,每一条线段对应一个长方形:4+3+2+1=10(个).,6.30个.图中AB边上共有线段4+3+2+1=10条.条线段作为长,BC边上每一条线段作为宽中共有长方形为:BC边上共有线段,每一个长配一个宽:2+1=3(条),把AB,就构成一个长方形上的每一,因此图(4+3+2+1)(2+1)=103=30(个).7.60个.图中,依照计算上图中长方形个数的方法(4+3+2+1)(3+2+1)=60(个).:可得长方形个数为:一般状况下,假如有似中的任一个方形一上有个端点),另一上有m 1个分点(不包含条的两个端点行且与另一订交,两平行将方形分多方形n 1个分点(不包含条的两),通些点分作的平,方形的数:(1+2+3+⋯⋯+m)（1+2+3+⋯⋯n）.共有90个.AB上分红的段有:5+4+3+2+1=15.BC上分红的段有:3+2+1=6.因此共有方形:(5+4+3+2+1)(3+2+1)=156=90(个).9.15个;45个.10.(3+2+1)(5+4+3+2+1)=615=90(个).二、解答:1.a:44+33+22+11=30(个)b:66+55+44+33+22+1=91(个)2.32个正方形.126个方形.3.a:10个.b:15个.4.15个.。

小学四年级奥数专项练习（八）一、数线段与长方形
（一）填空题
1.下列图形各有几条线段
( )条( )条
( )条
2.在一线段上任取21个点,(包
括两端点).则一共有( )条线
段。

3.图中一共有( )条线段:
4.图中一共有( )个角。

（二）解答题
1．下图中一共有几个长方形？
2．下图中长方形共有多少个？
二、组合图形的计数
1.右图一共有( )个长方形。

2. 右图共有几个正方形?
3. 在一个图案中有100个矩形、100
个菱形和40个正方形,这个图案中
至少有多少个平行四边形?
4．三个同样的正方形框架,摆放在适当的位置,最多可以数出多
少个正方形来?。

数线段与长方形一、填空题:1.下列图形各有几条线段( )条( )条( )条2.在一线段上任取21个点,(包括两端点).则一共有( )条线段.3.下图一共有( )条线段:4.下列图形中,一共有( )个角.5.数一数,下列图中一共有( )个角.6.一条直线上共有50个点,可以数出( )条线段.7.从一点引出10条射线,可以数出( )个小于1800的角.8.平面上有10个点,设有三点在一直线上的情况.这些点可以连成( )条线段.9.把一个三角形底边平均分成20等份，等分点与顶点相连,可以连成( )条线段.10.右图中，大大小小的长方形一共有( )个.二、解答题:1.右图中,一共有几个长方形?2.下图中一共有几个长方形？3.右图中大大小小的长方形共有多少个？4.右图中共有多少个长方形？———————————————答案——————————————————————分析与解答一、填空题:1. a有10条, b有15条, c有21条.2. (1+2+3+4+……+19+20) 点金术:如果线段上的基本线段有n条,则=(20+1)⨯20÷2 总的线段数为:=210(条). 1+2+3+4+……+n(-)1n+=÷1( 2n)⨯+n3. (1+2)⨯4+(3+2+1)⨯2 点金术:如果图形比较复杂时,可以先找出=12+12 线段条数相等的线段,再加起来.=24(条).4. 6+5+4+3+2+1 点金术:如果一个角内一共有几个基本角. =21(个). 则总的角(锐角)一共有( 2.+nn)1÷⨯5. (1+99)⨯99÷2=99⨯50=4950(个).6. 50⨯49÷2=1225(条).7. 10⨯9÷2=45(个).8. 10⨯9÷2=45(条).9. (1+20)⨯20÷2+19=229(个).10. (5+4+3+2+1)⨯1=15(个).二、解答题:1. 一共有(5+4+3+2+1)⨯(2+1)=45(个).2. 解:一共有90(个).(5+4+3+2+1)⨯(3+2+1)=(6⨯5÷2)⨯(4⨯3÷2)=15⨯6=90(个).注:一般地有如下规律:长方形个数=[(长边段数+1)⨯长边段数÷2]⨯[(宽边段数+1)⨯宽边段数÷2]3. 共有102个.解: ①长方形ABDE内包含的长方形的个数有:(6⨯5÷2)⨯(4⨯3÷2)=90(个).②长方形CDFG内包含的长方形个数有:(3⨯2÷2)⨯(5⨯4÷2)=30(个).③在上面的两项计算中,长方形CDEH内的长方形被重复计算了,这部分长方形的个数是:(3⨯2÷2)⨯(4⨯3÷2)=18(个).④图中共有长方形:90+30-18=102(个).4. 解: ①左边大长方形内有长方形:(5+4+3+2+1)⨯(7+6+5+4+3+2+1)=15⨯28=420(个).②下边大长方形内有长方形:(4+3+2+1)⨯(8+7+6+5+4+3+2+1)=10⨯36=360(个).③左下重复的长方形有:(4+3+2+1)⨯(7+6+5+4+3+2+1)=10⨯28=280(个).④图中共有长方形:420+360-280=500(个).。

第4讲巧数长（正）方形的个数数图形时要有次序、有条理，才能不遗漏、不重复，一般步骤应是：仔细观察，发现规律，应用规律。

长方形是用“点”或者“线”来数的，而正方形是用“块”来数的。

数长方形的公式：长边上的线段和×宽边上的线段和数正方形的公式：1、一个被划分成m×n的小正方形的长方形中共可以数出的正方形的个数是：m×n＋（m-1）×（n-1）＋（m-2）×（n-2）＋…………………………＋1×【n-（m-1）】（其中m<n）2、当m=n时，即一个划分成n×n=n2个小正方形的正方形中，共可以数出正方形的个数是：n2＋（n-1）2＋……………………＋22＋12典型例题：1、长方形的构成必须有长和宽，下图中有许多长方形，你能数出它们有多少个？分析与解答:因为长方形的构成与长的线段数有关，也与宽的线段数有关，所以数长方形的个数必须要看长与宽两个因素。

上图上长有6条线段，即3＋2＋1=6（个）宽边上有3条线段，即2＋1=3（个）因此，根据数长方形公式：6×3=18（个）答：上图中共有18个长方形。

2、下图中共有多少个长方形？分析与解答：这道题比例1横竖都多了一条线，那么长方形的个数明显增多了，利用公式仍然要数出长边上的线段数和宽边上的线段数即长边上的线段和：4＋3＋2＋1＝10个宽边上的线段和：3+2+1=6个因此根据数长方形公式：10×6=60个答：上图中共有60个长方形。

3、下图中共有多少个正方形？分析与解答：我们先来数一数：只含一个正方形的有9个（即3×3=9）；含有4个正方形的有4个（即2×2=4）；含有9个正方形的有1个。

通过刚才的数，我们发现图中正方形的个数为1×1+2×2+3×3=1+4+9=14个，以后我们碰到类似的题目可以用这种方法数出正方形的个数。

四年级几何奥数题
一、题目示例
1. 一个等腰三角形的顶角是底角的4倍，求这个等腰三角形的底角和顶角各是多少度？
解析：
因为等腰三角形的两个底角相等，设底角的度数为公式，则顶角的度数为公式。

根据三角形内角和为公式，可列出方程公式。

合并同类项得公式。

解得公式。

那么顶角公式。

所以这个等腰三角形的底角是公式，顶角是公式。

2. 长方形的长是12厘米，宽是8厘米，求这个长方形的对角线长度。

解析：
根据长方形的性质，对角线与长和宽构成直角三角形，长和宽为直角边，对角线为斜边。

由勾股定理公式（其中公式、公式为直角边，公式
为斜边）。

这里公式厘米，公式厘米。

则对角线公式厘米。

3. 一个平行四边形的底是10厘米，高是8厘米，如果底减少3厘米，高不变，那么面积减少多少平方厘米？
解析：
原来平行四边形的面积公式平方厘米。

底减少3厘米后，新的底为公式厘米。

此时平行四边形的面积公式平方厘米。

面积减少的值为公式平方厘米。

(完整版)小学四年级奥数题四年级综合练习一1、按规律填数（1）2、3、5、8、13、21、（）、（）……（2）9、18、54、5、10、30、7、（）、（）2、在0、2、4、8、7和5 这六个数中选5 个数组成最大的五位数是（），最小的五位数是（）。

3、被减数、减数、差三个数相加等于456，被减数是（）。

4、爷爷和父亲今年共167岁，五年前，爷爷比父亲大35岁，爷爷今年是（）岁。

5、三年级有男生218人，比女生的2倍少12人。

女生（）人。

6、一具数它的千万位上和万位上基本上6，其它各个数位上基本上0，那个数是（）。

7、今年的5月1日是星期三，六月1日是星期（）。

8、跳绳竞赛规定每人跳5分钟，王平跳了375下，张华平均每分钟比王多跳了5下，张华一共跳了（）下。

9、知识比赛，一共20题。

答对一题得6分，答错一题扣3分，没答得0 分，小亮得了102分，他答对了（）题。

10、李华在计算有余数的除法时，把被除数237错写成261。

如此商比原来多了2，而余数正好相同。

这道题的除数是（），余数是（）。

11、三（1）班有45人，29人参加数学小组，16人参加语文小组。

11人两个小组都参加。

有（）个人两组都没有参加。

12、哥哥把自个儿的书送8本给妹妹，如此妹妹依然比哥哥少7本，哥哥比妹妹原来多（）本书。

13、用23条短绳接成一条长绳，需要打（）个结。

14、一段路长20米，在它的两旁种树，每4 米种一棵，共要种（）棵树。

15、已知：□+△=300 ，□×4=248，求△=（），□=（）练习二4、小强从一楼爬到三楼要用24秒，照如此计算，小强从五楼爬到十楼要用多少秒？5、粮库内有一批面粉，第一次运出总数的一半多3吨，第二次运出剩下的一半又7 吨，还剩下4吨。

咨询粮库里原有面粉多少吨？6、从第一堆西瓜里拿出一半放到第二堆里，再拿35个放到第三堆里，又拿出剩下的一半放到第四堆里。

最终第一堆还有15个。

第一堆原有多少个西瓜？7、买一把椅子和一张桌子共198元，一张桌子的价钞票是一把椅子的3倍，一把椅子的价钞票是多少？8、王老师带三⑵同学去游湖心公园，全班共有42个同学，他们租足踏船游湖，每只船限乘8人。

四年级数线段的图形题
一、学习目标
1.知道线段上端点的个数与线段的条数之间的关系。

2.通过数图形的个数,归纳、概括、总结与图形个数有关的规律，会用式子表示规律。

3.初步提高归纳和概括能力。

二、根据统计表中的数据回答问题。

颜色红花黄花蓝花粉花
盆数8 7 5 6
1. (红)色的花最多，( ）色的懿最少。

2.红花比蓝花多（）盆。

典题精讲
图中，包含“*”号的三角形有()个。

三、解题思路：
要确定含有五角星的正方形的个数，我们可以按正方形的边长是几个单位来思考，边长是1个单位的小正方形有1个，边长是2个单位的小正方形有2×2=4(个)，边长是3个单位的小正方形的个数是1，这样一共有1+4+1=6(个)。

线段图解题主要内容：1、线段图解题的方法和技巧；2、常见的可以用线段图来表示的数量关系；3、用线段图解题。

重难点：1、常见的可以用线段图来表示的数量关系；2、较复杂的线段图问题。

意义：利用线段图解决应用题是数学中常见的一种解题方法。

相比于传统的文字分析方法，线段图可以直观清晰地将题中的复杂数量关系展现在我们的眼前，对于理解题意和解决问题有十分重要的作用。

一、线段图解题方法和技巧：什么是线段？那就是一条直线上的两个点和它们之间的部分就叫做线段，线段的长度是有限的，所以我们常用来表示有限的量，帮助我们分析题目中隐藏的数量关系，达到轻松解题的目的。

1、用线段的长短来表示量的大小，并对应的标上数据；2、根据题意，有的可能只需要一条线段，有的可能需要多条线段；3、画多条线段时，要一端对齐，方便比较大小；4、画多条线段时，一般先画最小的量。

5、虚实结合。

“比……多”时，多的部分画实线；“比……少”时，少的部分画虚线，且立即标上数据；二、常见的可以用线段图来表示的数量关系1、和的关系：用一条较长线段来表示“和”，将组成“和”的各分量依次标在该线段上。

当出现多种数量关系时，和关系还可以用大括号来表示。

例如：甲的文具数量为5个，乙的文具数量为2个，那么甲乙的和是多少？2、差的关系：从小到大依次画出各个量，并保持一端对齐后，另一端多出的部分线段即可表示量与量之间的差。

例如：数学考试后小明的得分为100分，小强的得分为95分，那么小强比甲的5个乙的2个7个文具小明少几分？小强的得分：小明的得分：3、倍的关系：先画出最小的量，再画跟它成倍数关系的量，是它的几倍就画几段线段。

可将最小的量看作1份，则其它的量是它的几倍，就是几份。

例如：甲的年龄为5岁，乙的年龄为甲的3倍，那么乙的年龄为几岁？甲的年龄：乙的年龄：注意：在同一个问题中，一条线段只能代表一个数量（若两个数量相等，则可用等长的线段来表示），与这个数量有大小或倍数关系的其它数量应该在这条线段的长度上分别延长（或缩短或等长延长）来表示。