第14章 弹簧
- 格式:ppt
- 大小:3.85 MB
- 文档页数:30




第1节机械振动知识点一| 简谐运动的特征1.简谐运动(1)定义:如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动。
(2)平衡位置:物体在振动过程中回复力为零的位置。
(3)回复力①定义:使物体返回到平衡位置的力。
②方向:总是指向平衡位置。
③来源:属于效果力,可以是某一个力,也可以是几个力的合力或某个力的分力。
2.简谐运动的两种模型[(1)简谐运动的平衡位置就是质点所受合力为零的位置。
(×)(2)做简谐运动的质点先后通过同一点,回复力、速度、加速度、位移都是相同的。
(3)做简谐运动的质点,速度增大时,其加速度一定减小。
(√)简谐运动的“五个特征”1.动力学特征:F =-kx ,“-”表示回复力的方向与位移方向相反,k 是比例系数,不一定是弹簧的劲度系数。
2.运动学特征:简谐运动的加速度的大小与物体偏离平衡位置的位移的大小成正比,而方向相反,为变加速运动,远离平衡位置时,x 、F 、a、E p 均增大,v 、E k 均减小,靠近平衡位置时则相反。
3.运动的周期性特征:相隔T 或nT 的两个时刻,振子处于同一位置且振动状态相同。
4.对称性特征(1)相隔T 2或(2n +1)2T (n 为正整数)的两个时刻,振子位置关于平衡位置对称,位移、速度、加速度大小相等,方向相反。
(2)如图所示,振子经过关于平衡位置O 对称的两点P 、P ′(OP =OP ′)时,速度的大小、动能、势能相等,相对于平衡位置的位移大小相等。
(3)振子由P 到O 所用时间等于由O 到P ′所用时间,即t PO =t OP′。
(4)振子往复过程中通过同一段路程(如OP 段)所用时间相等,即t OP =t PO 。
5.能量特征:振动的能量包括动能E k 和势能E p ,简谐运动过程中,系统动能与势能相互转化,系统的机械能守恒。
[典例] (多选)如图所示,一轻质弹簧上端固定在天花板上,下端连接一物块,物块沿竖直方向以O 点为中心点,在C 、D 两点之间做周期为T 的简谐运动。
P第十四章 结构的稳定计算14.1 两类稳定问题概述一、结构设计应满足三方面的要求1、强度2、刚度3、稳定性。
二、基本概念1、失稳:当荷载达到某一数值时,体系由稳定平衡状态转变为不稳定状态,而丧失原始平衡状态的稳定性,简称“失稳”。
工程中由于结构失稳而导致的事故时有发生,如加拿大魁北克大桥、美国华盛顿剧院的倒塌事故,1983年北京某科研楼兴建中的脚手架的整体失稳等,都是工程结构失稳的典型例子。
2、临界状态:由稳定平衡状态过度到不稳定状态的中间状态(中性平衡状态)。
3、临界荷载:临界状态时相应的荷载。
三、结构失稳的两种基本形式1、第一类失稳(分支点失稳):结构变形产生了性质上的突变,带有突然性。
2、第二类失稳(极值点失稳):虽不出现新的变形形式,但结构原来的变形将增大或材料的应力超过其许可值,结构不能正常工作。
c rc r14.2 确定临界荷载的静力法和能量法一、静力法1、临界状态的静力特征(1)体系失稳前在弹性阶段工作a 、应力、应变成线性关系。
b 、挠曲线近似微分方程成立。
(2)静力特征临界荷载具有“平衡状态的二重性”,因为它是由稳定平衡状态过渡到不稳定状态的极限状态。
2、定义:假定体系处于微弯失稳的临界状态,列出相应的平衡微分方程,进而求解临界荷载的方法。
3、步骤:(1)建立坐标系、取隔离体、绘受力图。
(2)列静力平衡方程。
(3)将挠曲线方程代入平衡方程后,利用边界条件求稳定方程。
(4)解稳定方程,求临界荷载。
4、举例 试求图示结构的临界荷载。
x解“超越方程”的两种方法: 1、逐步逼近法(试算法):2、图解法:以αl 为自变量,分别绘出z= αl 和 z=tg αl 的图形,求大于零的第一个交点, 确定αl 。
取最小根αl =4.493例14−1 图14−6(a )所示一端固定、一端自由的杆件,BC 段为刚性,A B 段弯曲刚度为EI 。
试建立临界荷载的稳定方程。
解:任一截面的弯矩为稳定方程为展开次行列式得((二、能量法1、用能量原理建立的能量准则(适用于单自由度体系)(1)三种平衡状态a 、稳定平衡: 偏离平衡位置,总势能增加。


压强和浮力计算题分类总结及强化练习【1】固体压强涉及到的公式主要为:F 压=G=mg (水平面) P=F/S m=Ρv f=F 牵(匀速直线运动) V=S/t一、与人或者动物有关的题目,注意:受力面积是一只脚还是两只脚,无论是单脚站立还是双脚站立对地面的压力都不变例1、小理同学的质量为50kg ,他站立在承平地面时,双脚鞋底与地面接触面积约为0.04m 2.求:(1)小理同学的重力;(2)小理同学对地面的压强。
(3)小理同学单脚站立时对地面的压强。
解:已知:m=50kg S 双=0.04m 2 S 单=1/2 S 双=0.02m 2 g=10N/kg (1)G=mg=50kg ×10N/kg=500N(2)F=G=500N P=F/S=500N/0.04m 2=1.25×104 Pa(3)方法一: 由于小理同学单脚站立时,重力未变,压力也没变即F=500N/ 0.02m 2 =2.5×104 Pa 方法二:由于小理同学单脚站立时,重力未变对地面的压力也没变,即:P 单/P 双=S 双/S 单 P 单/1.25×104 Pa =0.04m 2//0.02m 2 P 单=2.5×104 Pa例2、一头大象的质量为3t ,大象一只脚掌与地面接触面积为0.2 m 2,求:(1)该大象的重力(2)大象抬起一只脚对地面的压力和压强二,与物体有关的考题例1、建设工地的压桩机常会用到一种如图12所示长方体混凝土块。
求:(1)混凝土块的体积。
(2)混凝土块的质量。
(3)混凝土块受到的重力。
(4)混凝土块平放时对地面的压强。
(混凝土的密度为2.8×103kg/m 3)例2、杨丹同学对实验室的显微镜发生了浓厚的兴趣,他用台秤测量出它的质量为2kg ,用直尺测量并经过简单计算得出它的底面积为0.04m 2,当显微镜放在水平桌面上时.求:(1)显微镜所受的重力多大?(2)它对水平桌面的压强有多大?三、与车辆有关的题目,注意题目中车轮的受力面积是否是全部车轮的面积例1、我国自行研发的纯电动中巴车的质量约为2000kg ,静止时轮胎与路面接触的总面积约0.2m 2,以30m/s 的速度沿水平路面匀速行驶时牵引力为2400N 。


第十四章流变学基础第一节概述一、流变学的基本概念(一)流变学研究内容流变学—Rheology来源于希腊的Rheos=Sream(流动)词语,是Bingham和Crawford 为了表示液体的流动和固体的变形现象而提出来的概念。
流变学主要是研究物质的变形和流动的一门科学。
对某一物体外加压力时,其内部各部分的形状和体积发生变化,即所谓的变形。
对固体施加外力,固体内部存在一种与外力相对抗的内力使固体保持原状。
此时在单位面积上存在的内力称为内应力(stress)。
对于外部应力而产生的固体的变形,当去除其应力时恢复原状的性质称为弹性(elasticity)。
把这种可逆性变形称为弹性变形(elastic deformation),而非可逆性变形称为塑形变形(plastic deformation)。
流动是液体和气体的主要性质之一,流动的难易程度与流体本身的粘性(viscosity)有关,因此流动也可视为一种非可逆性变形过程。
实际上,多数物质对外力表现为弹性和粘性双重特性,称为粘弹性物质。
(二)剪切应力与剪切速度观察河道中流水,水流方向一致,但水流速度不同,中心处的水流最快,越靠近河岸的水流越慢。
因此在流速不太快时可以将流动着的液体视为互相平行移动的液层,叫层流,如图14-1。
由于各层的速度不同,便形成速度梯度du/dy,或称剪切速度。
这反映流体流动的特征。
由于流动阻力便产生速度梯度,流动较慢的液层阻滞着流动较快液层的运动。
使各液层间产生相对运动的外力叫剪切力,在单位液层面积(A)上所需施加的这种力称为剪切应力,简称剪切力(shearing force),单位为N·m-2,以S表示。
剪切速度(rate of shear),单位为s-1,以D表示。
剪切应力与剪切速度是表征体系流变性质的两个基本参数。
图14-1 流动时形成的速度梯度二、流变学在药剂学中的应用流变学在药学研究中的重要意义在于可以应用流变学理论对乳剂、混悬剂、半固体制剂等的剂型设计、处方组成以及制备、质量控制等进行评价。
![理论力学第十四章 拉格朗日方程 [同济大学]](https://uimg.taocdn.com/183a560f16fc700abb68fc0b.webp)
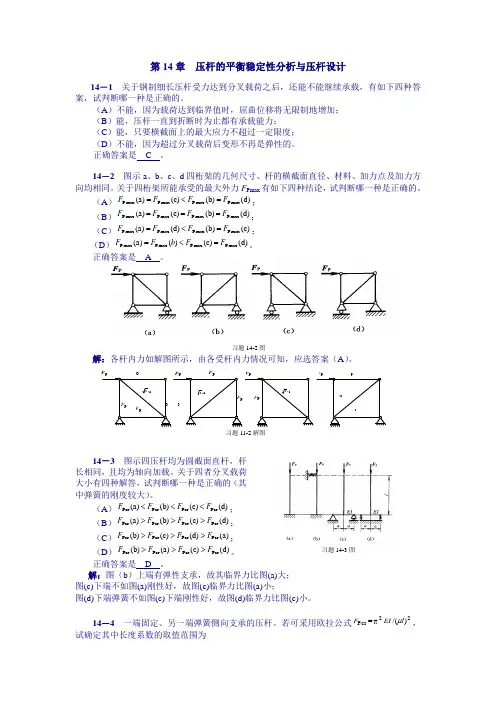
习题14-2图习题14-3图P F P F P F P F 0PF P -F 2F -2F 2F -2F 0000000P F P F PF P -F P-F P -F P F P F P F P F 0P F P -F 2F -2F 2F -2F 0000P F PF P F P-F P -F P -F 00习题11-2解图 第14章 压杆的平衡稳定性分析与压杆设计14-1 关于钢制细长压杆受力达到分叉载荷之后,还能不能继续承载,有如下四种答案,试判断哪一种是正确的。
(A )不能,因为载荷达到临界值时,屈曲位移将无限制地增加; (B )能,压杆一直到折断时为止都有承载能力; (C )能,只要横截面上的最大应力不超过一定限度; (D )不能,因为超过分叉载荷后变形不再是弹性的。
正确答案是 C 。
14-2 图示a 、b 、c 、d 四桁架的几何尺寸、杆的横截面直径、材料、加力点及加力方向均相同。
关于四桁架所能承受的最大外力F Pmax 有如下四种结论,试判断哪一种是正确的。
(A ))d ()b ()c ()a (max P max P max P max P F F F F =<=; (B ))d ()b ()c ()a (max P max P max P max P F F F F ===; (C ))c ()b ()d ()a (max P max P max P max P F F F F =<=;(D ))d ()c ()()a (max P max P max P max P F F b F F =<=。
正确答案是 A 。
解:各杆内力如解图所示,由各受杆内力情况可知,应选答案(A )。
14-3 图示四压杆均为圆截面直杆,杆长相同,且均为轴向加载。
关于四者分叉载荷大小有四种解答,试判断哪一种是正确的(其中弹簧的刚度较大)。
(A ))d ()c ()b ()a (Pcr Pcr Pcr Pcr F F F F <<<; (B ))d ()c ()b ()a (Pcr Pcr Pcr Pcr F F F F >>>; (C ))a ()d ()c ()b (Pcr Pcr Pcr Pcr F F F F >>>;(D ))d ()c ()a ()b (Pcr Pcr Pcr Pcr F F F F >>>。
第14章 轴向拉伸与压缩14-1 用截面法求图14-1(a )(b )(c )所示各杆指定截面的内力。
(a ) (b )(c )图14-1解:(a )1. 用截面1-1将杆截开,取左段为研究对象,作受力图,由平衡方程 0X =∑得 10N =2. 用截面2-2将杆截开,取左段为研究对象,作受力图,由平衡方程 0X =∑,20N P -=得 2N P =3. 用截面3-3将杆截开,取左段为研究对象,作受力图,由平衡方程 0X =∑,30N P -=得 3N P =(b )1. 用截面1-1将杆截开,取左段为研究对象,作受力图,由平衡方程 0X =∑,12202N kN ⨯-= 得 12N k N = 2. 用截面2-2将杆截开,取左段为研究对象,作受力图,由平衡方程 0X =∑,220N kN -=得 12N k N =(c )1. 用截面1-1将杆截开,取右段为研究对象,作受力图,由平衡方程 0X =∑,130N P P --+=得 12N P =-2. 用截面2-2将杆截开,取右段为研究对象,作受力图,由平衡方程 0X =∑,20P N -=得 2N P =14-2 试计算图14-2(a )所示钢水包吊杆的最大应力。
已知钢水包及其所盛钢水共重90kN ,吊杆的尺寸如图(b )所示。
(b ) (c )图14-2解:吊杆的轴力90N kN =。
吊杆的危险截面必在有圆孔之处,如图14-2(c )所示,它们的截面积分别为22321(656520) 2.92510A mm m -=-⨯=⨯2322(104606018) 5.1610A m m m -=⨯-⨯=⨯ 2323[11860(6018)2] 4.9210A m m m -=⨯-⨯⨯=⨯ 显然,最小截面积为321 2.92510A m -=⨯,最大应力产生在吊杆下端有钉空处 3max 31190102215.382.92510P N MPa A A σ-⨯====⨯14-3 一桅杆起重机如图14-3所示,起重杆AB 为一钢管,其外径20D mm =,内径18d mm =;钢绳CB 的横截面积为20.1cm 。