MAAB产生各种分布的随机数

M A T L A B产生各种分布的随机数The final revision was on November 23, 2020MATLAB产生各种分布的随机数1，均匀分布U（a,b）：产生m*n阶［a，b］均匀分布U（a，b）的随机数矩阵：unifrnd (a,b,m, n) 产生一个［a，b］均匀分布的随机数：unifrnd (a,b)2，0-1分布U（0,1）产生m*n阶［０，1］均匀分布的随机数矩阵：rand (m, n)产生一个［０，１］均匀分布的随机数：rand4，二类分布binornd(N,P,mm,nn)如binornd(10,,mm,nn)即产生mm*nn均值为N*P的矩阵binornd(N,p)则产生一个。

而binornd(10,,mm)则产生mm*mm的方阵，军阵为N*p。

5，产生m*n阶离散均匀分布的随机数矩阵：unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵6，产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd( ,mm, nn)此外，常用逆累积分布函数表函数名调用格式函数注释norminv X=norminv(P,mu,sigma) 正态逆累积分布函数expinv X=expinv(P,mu) 指数逆累积分布函数weibinv X=weibinv(P,A,B) 威布尔逆累积分布函数logninv X=logninv(P,mu,sigma) 对数正态逆累积分布函数Chi2inv X=chi2inv(P,A,B) 卡方逆累积分布函数Betainv X=betainv(P,A,B) β分布逆累积分布函数随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N，P的二项随机数据函数 binornd格式 R = binornd(N,P) %N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，N、P大小相同。

R = binornd(N,P,m) %m指定随机数的个数，与R同维数。

matlab中随机数生成无题在MATLAB中，我们可以使用随机数生成函数来生成各种类型的随机数。

这些随机数可以用于模拟实验、数据分析、算法测试等方面。

在这篇文章中，我将介绍一些常用的随机数生成函数，并给出一些实际应用的例子。

一、rand函数rand函数用于生成0到1之间均匀分布的随机数。

例如，我们可以使用rand函数来模拟抛硬币的结果，生成0或1的随机数，其中0表示正面，1表示反面。

下面是一个示例代码：```matlabresult = rand(1, 100); % 生成100个0到1之间的随机数heads = sum(result < 0.5); % 统计正面的次数tails = sum(result >= 0.5); % 统计反面的次数fprintf('正面的次数：%d\n', heads);fprintf('反面的次数：%d\n', tails);```二、randn函数randn函数用于生成服从标准正态分布（均值为0，方差为1）的随机数。

这在统计学中经常用到。

我们可以使用randn函数来模拟一组身高数据，然后计算平均身高和标准差。

下面是一个示例代码：```matlabheights = randn(1, 1000) * 10 + 170; % 生成1000个身高数据，均值为170，标准差为10average_height = mean(heights); % 计算平均身高std_height = std(heights); % 计算标准差fprintf('平均身高：%f\n', average_height);fprintf('身高标准差：%f\n', std_height);```三、randi函数randi函数用于生成指定范围内的整数随机数。

例如，我们可以使用randi函数来模拟投掷骰子的结果，生成1到6之间的整数随机数。

matlab的random用法
Matlab中的random函数用于生成随机数，可用于模拟实验、数据分析、密码学、游戏等方面。

具体使用方式如下：
1. 生成随机整数：使用randi函数，输入两个参数，分别表示随机数的范围。

例如，生成1到10之间的随机整数，代码为：
randi([1,10])。

2. 生成随机小数：使用rand函数，输入一个参数，表示随机数的个数。

例如，生成10个0到1之间的随机小数，代码为：rand(10,1)。

3. 生成符合特定分布的随机数：使用randn、randp、randexp、randg等函数，分别表示标准正态分布、泊松分布、指数分布、正态分布等。

例如，生成10个符合标准正态分布的随机数，代码为：randn(10,1)。

4. 生成随机排列：使用randperm函数，输入一个参数，表示随机排列的长度。

例如，生成1到10的随机排列，代码为：randperm(10)。

注意：在使用random函数时，需要先设置随机数种子，可以使用rng函数。

例如，设置随机数种子为0，代码为：rng(0)。

这样可以保证每次生成的随机数相同。

- 1 -。

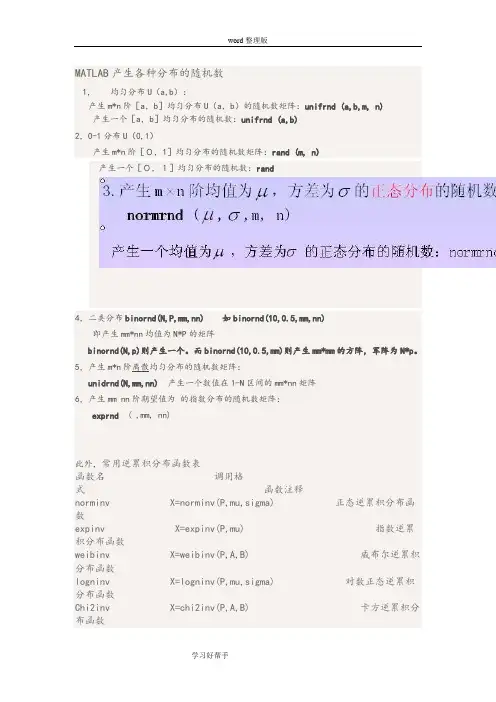
MATLAB产生各种分布的随机数1，均匀分布U（a,b）：产生m*n阶［a，b］均匀分布U（a，b）的随机数矩阵：unifrnd (a,b,m, n)产生一个［a，b］均匀分布的随机数：unifrnd (a,b)2，0-1分布U（0,1）产生m*n阶［０，1］均匀分布的随机数矩阵：rand (m, n)产生一个［０，１］均匀分布的随机数：rand4，二类分布binornd(N,P,mm,nn) 如binornd(10,0.5,mm,nn)即产生mm*nn均值为N*P的矩阵binornd(N,p)则产生一个。

而binornd(10,0.5,mm)则产生mm*mm的方阵，军阵为N*p。

5，产生m*n阶离散均匀分布的随机数矩阵：unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵6，产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd( ,mm, nn)此外，常用逆累积分布函数表函数名调用格式函数注释norminv X=norminv(P,mu,sigma) 正态逆累积分布函数expinv X=expinv(P,mu) 指数逆累积分布函数weibinv X=weibinv(P,A,B) 威布尔逆累积分布函数logninv X=logninv(P,mu,sigma) 对数正态逆累积分布函数Chi2inv X=chi2inv(P,A,B) 卡方逆累积分布函数Betainv X=betainv(P,A,B) β分布逆累积分布函数4.1 随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N，P的二项随机数据函数 binornd格式 R = binornd(N,P) %N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，N、P大小相同。

R = binornd(N,P,m) %m指定随机数的个数，与R同维数。

R = binornd(N,P,m,n) %m,n分别表示R的行数和列数例4-1>> R=binornd(10,0.5)R =3>> R=binornd(10,0.5,1,6)R =8 1 3 7 6 4>> R=binornd(10,0.5,[1,10])R =6 8 4 67 5 3 5 6 2>> R=binornd(10,0.5,[2,3])R =7 5 86 5 6>>n = 10:10:60;>>r1 = binornd(n,1./n)r1 =2 1 0 1 1 2>>r2 = binornd(n,1./n,[1 6])r2 =0 1 2 1 3 14.1.2 正态分布的随机数据的产生命令参数为μ、σ的正态分布的随机数据函数 normrnd格式 R = normrnd(MU,SIGMA) %返回均值为MU，标准差为SIGMA的正态分布的随机数据，R可以是向量或矩阵。

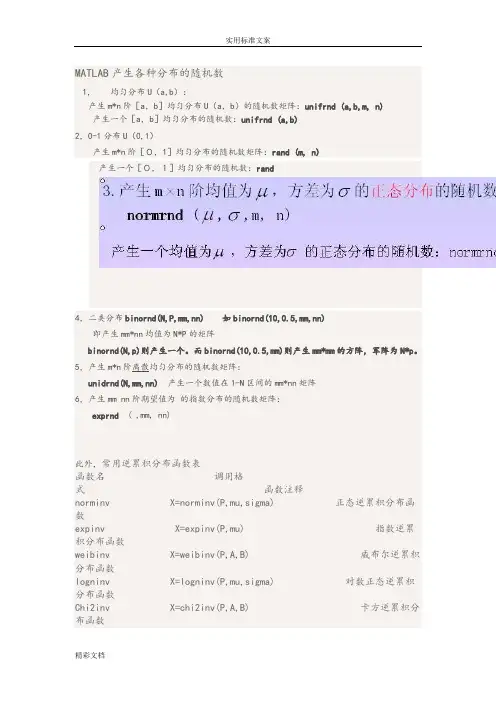
MATLAB产生各种分布的随机数1，均匀分布U（a,b）：产生m*n阶［a，b］均匀分布U（a，b）的随机数矩阵：unifrnd (a,b,m, n)产生一个［a，b］均匀分布的随机数：unifrnd (a,b)2，0-1分布U（0,1）产生m*n阶［０，1］均匀分布的随机数矩阵：rand (m, n)产生一个［０，１］均匀分布的随机数：rand4，二类分布binornd(N,P,mm,nn) 如binornd(10,0.5,mm,nn)即产生mm*nn均值为N*P的矩阵binornd(N,p)则产生一个。

而binornd(10,0.5,mm)则产生mm*mm的方阵，军阵为N*p。

5，产生m*n阶离散均匀分布的随机数矩阵：unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵6，产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd( ,mm, nn)此外，常用逆累积分布函数表函数名调用格式函数注释norminv X=norminv(P,mu,sigma) 正态逆累积分布函数expinv X=expinv(P,mu) 指数逆累积分布函数weibinv X=weibinv(P,A,B) 威布尔逆累积分布函数logninv X=logninv(P,mu,sigma) 对数正态逆累积分布函数Chi2inv X=chi2inv(P,A,B) 卡方逆累积分布函数Betainv X=betainv(P,A,B) β分布逆累积分布函数4.1 随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N，P的二项随机数据函数 binornd格式 R = binornd(N,P) %N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，N、P大小相同。

R = binornd(N,P,m) %m指定随机数的个数，与R同维数。

R = binornd(N,P,m,n) %m,n分别表示R的行数和列数例4-1>> R=binornd(10,0.5)R =3>> R=binornd(10,0.5,1,6)R =8 1 3 7 6 4>> R=binornd(10,0.5,[1,10])R =6 8 4 67 5 3 5 6 2>> R=binornd(10,0.5,[2,3])R =7 5 86 5 6>>n = 10:10:60;>>r1 = binornd(n,1./n)r1 =2 1 0 1 1 2>>r2 = binornd(n,1./n,[1 6])r2 =0 1 2 1 3 14.1.2 正态分布的随机数据的产生命令参数为μ、σ的正态分布的随机数据函数 normrnd格式 R = normrnd(MU,SIGMA) %返回均值为MU，标准差为SIGMA的正态分布的随机数据，R可以是向量或矩阵。

matlab产生泊松分布的随机数Matlab是一种强大的数值计算软件，可以用来产生符合泊松分布的随机数。

泊松分布是一种离散型概率分布，常用于描述单位时间（或单位面积）内随机事件发生的次数。

要在Matlab中产生泊松分布的随机数，可以使用内置的函数`poissrnd`。

这个函数的输入参数是泊松分布的均值lambda，输出是符合泊松分布的随机数。

下面我们通过一个简单的例子来演示如何使用Matlab产生泊松分布的随机数。

我们需要确定泊松分布的参数lambda。

lambda表示单位时间（或单位面积）内随机事件的平均发生次数。

假设某个事件的平均发生次数为3次，我们可以将lambda设置为3。

```matlablambda = 3;```接下来，我们可以使用`poissrnd`函数来产生符合泊松分布的随机数。

假设我们需要生成100个随机数，可以将函数的第一个参数设置为lambda，第二个参数设置为生成的随机数的个数。

```matlabrandom_numbers = poissrnd(lambda, 100, 1);```这样，`random_numbers`就是一个包含100个符合泊松分布的随机数的列向量。

我们可以将这些随机数进行可视化，以更直观地了解泊松分布的特性。

可以使用Matlab的绘图函数`histogram`来绘制随机数的直方图。

```matlabhistogram(random_numbers, 'Normalization', 'probability'); xlabel('随机数');ylabel('概率');title('泊松分布的随机数直方图');```通过观察直方图，我们可以看到随机数的分布形状接近一个正态分布，这是泊松分布的特性之一。

除了产生泊松分布的随机数，Matlab还提供了其他与泊松分布相关的函数。

matlab中随机数的产生摘要：随机数在MATLAB中有着广泛的应用，本文将介绍MATLAB中随机数产生的基本方法，以及如何在实际问题中应用随机数。

一、随机数产生的基本方法MATLAB提供了丰富的随机数生成函数，可以方便地产生各种类型的随机数。

以下是一些常用的随机数生成函数：1. rand(): 生成一个[0,1]区间内的随机小数。

2. randn(): 生成一个正态分布的随机数。

3. randi(M, N): 从整数序列{1, 2, ..., M}中随机选择一个整数，该整数满足N <= i <= M。

4. randperm(N): 生成一个随机排列的整数序列，长度为N。

5. randn(N): 生成一个Nx1的正态分布随机数行向量。

6. randn(m, n): 生成一个m行n列的正态分布随机数矩阵。

二、实际问题中的应用随机数在MATLAB中有着广泛的应用，以下是一些实际问题的应用示例：1. 蒙特卡罗模拟蒙特卡罗模拟是一种通过随机抽样来解决问题的方法。

在MATLAB中，可以使用randn()函数生成正态分布的随机数，然后通过蒙特卡罗模拟来求解实际问题。

例如，在金融领域，可以使用蒙特卡罗模拟来估算期货合约的价值。

2. 优化算法在优化算法中，随机数可以用于初始化变量或生成样本点。

例如，在遗传算法中，可以使用randi()函数随机生成初始种群。

在模拟退火算法中，可以使用rand()函数随机生成初始温度。

3. 信号处理在信号处理中，随机数可以用于模拟噪声信号。

例如，可以使用randn()函数生成高斯白噪声。

此外，还可以使用rand()函数生成随机相位，用于实现傅里叶变换中的随机相位编码。

4. 图像处理在图像处理中，随机数可以用于实现各种随机操作。

例如，可以使用randn()函数对图像进行高斯模糊。

使用randi()函数可以实现图像的随机像素替换。

使用randn()和rand()函数可以实现图像的随机颜色变换。

matlab随机数生成函数
Matlab中提供了多种随机数生成函数，可以根据不同的需求生成不同的随机数。

1.rand函数：rand函数可以生成均匀分布的随机数，可以指定生成的随机数的行数和列数，也可以指定生成的随机数的范围。

2.randn函数：randn函数可以生成正态分布的随机数，可以指定生成的随机数的行数和列数，也可以指定生成的随机数的均值和标准差。

3.randi函数：randi函数可以生成指定范围内的整数随机数，可以指定生成的随机数的行数和列数，也可以指定生成的随机数的最小值和最大值。

4.randperm函数：randperm函数可以生成一个指定范围内的随机排列，可以指定生成的随机排列的长度，也可以指定生成的随机排列的最小值和最大值。

5.rng函数：rng函数可以设置随机数生成器的种子，可以指定生
成的随机数的种子，也可以指定生成的随机数的类型，如均匀分布、正态分布等。

在MATLAB中生成0到1之间的高斯分布的随机数可以通过以下步骤实现：1. 导入MATLAB工具箱在MATLAB中进行任何操作之前，需要确保已经导入了Statistics and Machine Learning Toolbox工具箱，因为高斯分布的生成函数位于该工具箱中。

2. 使用randn函数生成高斯分布随机数在MATLAB中，可以使用randn函数来生成服从标准正态分布（均值为0，标准差为1）的随机数。

对生成的随机数进行线性变换，以使其均值为μ，标准差为σ。

具体操作如下：```matlabmu = 0; 均值sigma = 1; 标准差n = 1000; 生成1000个随机数r = mu + sigma.*randn(n,1); 生成均值为mu，标准差为sigma的高斯分布随机数```在这段代码中，mu表示所需的高斯分布的均值，sigma表示所需的高斯分布的标准差，n表示生成随机数的个数。

通过randn函数生成的随机数将被线性变换为均值为μ，标准差为σ的高斯分布随机数。

3. 调整生成的随机数范围如果需要将生成的随机数范围限定在0到1之间，可以通过线性变换的方法实现。

具体来说，可以使用MATLAB中的min和max函数来实现对随机数范围的调整，如下所示：```matlabr_adj = (r - min(r)) / (max(r) - min(r)); 调整随机数范围为0到1之间```通过这段代码，生成的随机数r将被调整为范围在0到1之间的r_adj。

总结通过以上步骤，就可以在MATLAB中生成0到1之间的高斯分布的随机数。

首先使用randn函数生成服从标准正态分布的随机数，然后通过线性变换调整均值和标准差，最终通过调整随机数范围实现生成0到1之间的高斯分布随机数。

这样的操作可以很好地满足实际需求，并且在MATLAB中具有很高的灵活性和可操作性。

生成高质量的高斯分布随机数在统计学、工程学以及计算机科学等领域中都具有重要的应用。

matlab产生随机数的方法第一种方法是用 random 语句，其一般形式为y = random('分布的英文名',A1,A2,A3,m,n)，表示生成 m 行 n 列的m × n 个参数为 ( A1 , A2 , A3 ) 的该分布的随机数。

例如:(1) R = random('Normal',0,1,2,4): 生成期望为 0,标准差为 1 的(2 行 4 列)2× 4 个正态随机数(2) R = random('Poisson',1:6,1,6): 依次生成参数为 1 到 6 的(1 行 6 列)6 个 Poisson 随机数第二种方法是针对特殊的分布的语句：一．几何分布随机数（下面的 P，m 都可以是矩阵）R = geornd(P) （生成参数为 P 的几何随机数）R = geornd(P,m) （生成参数为 P 的× m 个几何随机数）１ R = geornd(P,m,n) （生成参数为 P 的 m 行 n 列的m × n 个几何随机数）例如(1) R = geornd(1./ 2.^(1:6)) ( 生成参数依次为 1/2,1/2^2,到 1/2^6 的 6 个几何随机数)(2) R = geornd(0.01,[1 5]) (生成参数为 0.01 的（１行５列）5 个几何随机数).二．Beta 分布随机数R = betarnd(A,B) （生成参数为 A,B 的 Beta 随机数）R = betarnd(A,B,m) （生成× m 个数为 A,B 的 Beta 随机数）１R = betarnd(A,B,m,n) （生成 m 行 n 列的m × n 个数为 A,B 的 Beta 随机数）.三．正态随机数R = normrnd(MU，SIGMA) （生成均值为 MU，标准差为 SIGMA 的正态随机数）R = normrnd(MU，SIGMA,m) （生成1× m 个正态随机数）R = normrnd(MU，SIGMA,m,n) （生成 m 行 n 列的m × n 个正态随机数）例如(1) R = normrnd(0,1,[1 5]) 生成 5 个正态(0,1) 随机数(2) R = normrnd([1 2 3;4 5 6],0.1,2,3) 生成期望依次为[1,2,3;4,5,6], 方差为 0.1 的2× 3 个正态随机数．四．二项随机数：类似地有R = binornd(N,P) R = binornd(N,P,m) R = binornd(N,p,m,n) 例如n = 10:10:60; r1 = binornd(n,1./n) 或 r2 = binornd(n,1./n,[1 6]) （都生成参数分别为1 1 ), L, ( 60, ) 的６个二项随机数．(10,10 60五．自由度为 V 的χ 2 随机数：R = chi2rnd(V) R = chi2rnd(V R = chi2rnd(V,m),m,n)六．期望为 MU 的指数随机数（即Exp 随机数）：1MUR = exprnd(MU) R = exprnd(MU,m) R = exprnd(MU,m,n)七．自由度为 V1， V2 的 F 分布随机数：R = frnd(V1，V2) R = frnd(V1， V2,m) R = frnd(V1，V2,m,n)八．Γ ( A, λ ) 随机数：R = gamrnd（A,lambda） R = gamrnd（A,lambda,m) R = gamrnd （A,lambda,m,n)九．超几何分布随机数：R = hygernd(N,K,M) R = hygernd(N,K,M,m) R =hygernd(N,K,M,m,n)十．对数正态分布随机数R = lognrnd(MU，SIGMA) R = lognrnd(MU，SIGMA,m) R = lognrnd(MU，SIGMA,m,n)十一．负二项随机数：R = nbinrnd(r,p) R = nbinrnd(r,p,m) R = nbinrnd(r,p,m,n)十二．Poisson 随机数：R = poissrnd(lambda) R = poissrnd(lambda,m) R =poissrnd(lambda,m,n)例如，以下 3 种表达有相同的含义：lambda = 2; R =poissrnd(lambda,1,10)（或 R = poissrnd(lambda,[1 10]) 或 R = poissrnd(lambda(ones(1,10)))十三．Rayleigh 随机数：R = raylrnd(B) R = raylrnd(B,m) R = raylrnd(B,m,n)十四．V 个自由度的 t 分布的随机数：R = trnd(V) R = trnd(V,m) R = trnd(V,m,n)42十五．离散的均匀随机数：R = unidrnd(N) R = unidrnd(N,m) R = unidrnd(N,m,n)十六．[A,B] 上均匀随机数R = unifrnd(A,B) R = unifrnd(A,B,m) R = unifrnd(A,B,m,n)例如 unifrnd(0,1:6)与 unifrnd(0,1:6,[1 6]) 都依次生成[0,1] 到[0,6]的６个均匀随机数．:十七．Weibull 随机数R = weibrnd(A,B) R = weibrnd(A,B,m) R = weibrnd(A,B,m,n)MATLAB中产生高斯白噪声的两个函数MATLAB中产生高斯白噪声非常方便，可以直接应用两个函数，一个是WGN，另一个是AWGN。

MATLAB产生各种分布的随机数1，均匀分布U（a,b）：产生m*n阶［a，b］均匀分布U（a，b）的随机数矩阵：unifrnd (a,b,m, n)产生一个［a，b］均匀分布的随机数：unifrnd (a,b)2，0-1分布U（0,1）产生m*n阶［０，1］均匀分布的随机数矩阵：rand (m, n)产生一个［０，１］均匀分布的随机数：rand4，二类分布binornd(N,P,mm,nn) 如binornd(10,0.5,mm,nn)即产生mm*nn均值为N*P的矩阵binornd(N,p)则产生一个。

而binornd(10,0.5,mm)则产生mm*mm的方阵，军阵为N*p。

5，产生m*n阶离散均匀分布的随机数矩阵：unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵6，产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd( ,mm, nn)此外，常用逆累积分布函数表函数名调用格式函数注释norminv X=norminv(P,mu,sigma) 正态逆累积分布函数expinv X=expinv(P,mu) 指数逆累积分布函数weibinv X=weibinv(P,A,B) 威布尔逆累积分布函数logninv X=logninv(P,mu,sigma) 对数正态逆累积分布函数Chi2inv X=chi2inv(P,A,B) 卡方逆累积分布函数Betainv X=betainv(P,A,B) β分布逆累积分布函数4.1 随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N，P的二项随机数据函数 binornd格式 R = binornd(N,P) %N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，N、P大小相同。

R = binornd(N,P,m) %m指定随机数的个数，与R同维数。

R = binornd(N,P,m,n) %m,n分别表示R的行数和列数例4-1>> R=binornd(10,0.5)R =3>> R=binornd(10,0.5,1,6)R =8 1 3 7 6 4>> R=binornd(10,0.5,[1,10])R =6 8 4 67 5 3 5 6 2>> R=binornd(10,0.5,[2,3])R =7 5 86 5 6>>n = 10:10:60。

matlab的random用法
random是matlab中的一个函数，用于生成随机数。

其使用方法如下：
1. 生成一个随机数：
rand
该命令将生成一个0到1之间的随机数。

2. 生成一个n行m列的随机数矩阵：
rand(n,m)
该命令将生成一个由n行m列的随机数矩阵。

3. 生成一个n维的随机向量：
randn(n,1)
该命令将生成一个由n个元素的随机向量。

4. 生成一个随机整数：
randi(range)
该命令将随机生成一个在range范围内的整数。

5. 生成一组服从正态分布的随机数：
normrnd(mean,sd)
该命令将生成一组服从均值为mean，标准差为sd的正态分布随机数。

6. 生成一组服从二项分布的随机数：
binornd(n,p)
该命令将生成一组服从n次实验，成功概率为p的二项分布随机
数。

7. 生成一组服从泊松分布的随机数：
poissrnd(lambda)
该命令将生成一组服从参数为lambda的泊松分布随机数。

注意：以上命令只是随机数生成的一些基本操作，matlab还有很多其他的随机数生成函数，可以根据需要选择使用。

MATLAB产生各种分布的随机数1，均匀分布U（a,b）：产生m*n阶［a，b］均匀分布U（a，b）的随机数矩阵：unifrnd (a,b,m, n)产生一个［a，b］均匀分布的随机数：unifrnd (a,b)2，0-1分布U（0,1）产生m*n阶［０，1］均匀分布的随机数矩阵：rand (m, n)产生一个［０，１］均匀分布的随机数：rand4，二类分布binornd(N,P,mm,nn) 如binornd(10,0.5,mm,nn)即产生mm*nn均值为N*P的矩阵binornd(N,p)则产生一个。

而binornd(10,0.5,mm)则产生mm*mm的方阵，军阵为N*p。

5，产生m*n阶离散均匀分布的随机数矩阵：unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵6，产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd( ,mm, nn)此外，常用逆累积分布函数表函数名调用格式函数注释norminv X=norminv(P,mu,sigma) 正态逆累积分布函数expinv X=expinv(P,mu) 指数逆累积分布函数weibinv X=weibinv(P,A,B) 威布尔逆累积分布函数logninv X=logninv(P,mu,sigma) 对数正态逆累积分布函数Chi2inv X=chi2inv(P,A,B) 卡方逆累积分布函数Betainv X=betainv(P,A,B) β分布逆累积分布函数4.1 随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N，P的二项随机数据函数binornd格式R = binornd(N,P) %N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，N、P大小相同。

R = binornd(N,P,m) %m指定随机数的个数，与R同维数。

R = binornd(N,P,m,n) %m,n分别表示R的行数和列数例4-1>> R=binornd(10,0.5)R =3>> R=binornd(10,0.5,1,6)R =8 1 3 7 6 4>> R=binornd(10,0.5,[1,10])R =6 8 4 67 5 3 5 6 2>> R=binornd(10,0.5,[2,3])R =7 5 86 5 6>>n = 10:10:60;>>r1 = binornd(n,1./n)r1 =2 1 0 1 1 2>>r2 = binornd(n,1./n,[1 6])r2 =0 1 2 1 3 14.1.2 正态分布的随机数据的产生命令参数为μ、σ的正态分布的随机数据函数normrnd格式R = normrnd(MU,SIGMA) %返回均值为MU，标准差为SIGMA的正态分布的随机数据，R可以是向量或矩阵。

M A T L A B产生各种分布的随机数Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】MATLAB产生各种分布的随机数1，均匀分布U（a,b）：产生m*n阶［a，b］均匀分布U（a，b）的随机数矩阵：unifrnd (a,b,m, n)产生一个［a，b］均匀分布的随机数：unifrnd (a,b)2，0-1分布U（0,1）产生m*n阶［０，1］均匀分布的随机数矩阵：rand (m, n)产生一个［０，１］均匀分布的随机数：rand4，二类分布binornd(N,P,mm,nn)如binornd(10,,mm,nn)即产生mm*nn均值为N*P的矩阵binornd(N,p)则产生一个。

而binornd(10,,mm)则产生mm*mm的方阵，军阵为N*p。

5，产生m*n阶离散均匀分布的随机数矩阵：unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵6，产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd( ,mm, nn)此外，常用逆累积分布函数表函数名调用格式函数注释norminvX=norminv(P,mu,sigma)正态逆累积分布函数expinvX=expinv(P,mu)指数逆累积分布函数weibinvX=weibinv(P,A,B)威布尔逆累积分布函数logninvX=logninv(P,mu,sigma)对数正态逆累积分布函数Chi2invX=chi2inv(P,A,B)卡方逆累积分布函数BetainvX=betainv(P,A,B)β分布逆累积分布函数随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N，P的二项随机数据函数 binornd格式 R = binornd(N,P) %N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，N、P大小相同。

R = binornd(N,P,m) %m指定随机数的个数，与R同维数。

matlab的random用法
Matlab中的random函数是用来生成随机数的，常见的用法有： 1. random('unif',a,b,n)：生成n个服从[a,b]均匀分布的随机数。

2. random('norm',mu,sigma,n)：生成n个服从均值为mu，标准差为sigma的正态分布的随机数。

3. random('poiss',lambda,n)：生成n个服从参数为lambda的泊松分布的随机数。

4. random('binom',n,p,k)：生成一个n次试验，每次成功概率为p的二项分布随机变量，取值为k。

5. random('exp',lambda,n)：生成n个服从参数为lambda的指数分布的随机数。

除了这些常见用法外，random函数还可以根据不同的分布类型生成不同的随机数，如伽马分布、负二项分布等。

在使用random函数时，需要根据具体的问题选择合适的分布类型及其参数。

- 1 -。