下载文档原格式
第10章五轴加工刀具路径五轴加工是在三轴的基础上加上两个回转轴进行的加工，对于目前的许多五轴加工中心，主轴可以为立式的，也可以调整为卧式的。
因此，从原理上讲，五轴加工可以加工五面体和任意形状的曲面。
但是，五轴加工中心用于倾斜的转动轴的转动角度，由于机床结构的限制，总有一个极限值，对于加工陡斜的曲面，读者要考虑机床结构极限的限制。
CNC机床中的第四轴和第五轴是可以绕X、Y或Z轴旋转的任意一个轴，通常是用A、B或C表示，具体是哪根轴，则根据机床的配置来定。
五轴加工相对三轴加工而言，有很多优越性，如扩大了加工范围、提高了加工效率、提高了加工精度等，因此，目前有许多学者从事这方面的研究。
五轴加工相对三轴加工要复杂得多，目前开发出的生成五轴加工刀具路径方法远比三轴加工的方法少得多，正处于研究与应用共存的阶段。
MasterCAM提供了四种产生五轴加工刀具路径的方法，即曲线五轴加工、钻削五轴加工、倾斜面五轴加工和曲面五轴流线加工方法，对于曲面加工而言，只有后两种方法可以应用。
MasterCAM提供的五轴曲面加工方法，没有过切检查功能，只能针对特定情况。
MasterCAM 相对其他CAD/CAM软件在五轴加工上，功能基本一样，但是在MasterCAM第九版中，增加了曲面五轴流线加工多曲面片的方法，这一点要领先于其他CAD/CAM软件，且有很大的实用价值。
MasterCAM生成CNC机床加工代码时，要用到后处理程序，对于不同的控制器，如法那克（Fanuc）、西门子（Siemens）等，要用不同的后处理程序。
对于五轴加工而言，目前MasterCAM软件还没有商品化的五轴加工后处理程序，需要单独开发，本书作者已掌握开发五轴加工后处理程序的方法，并在MAHO加工中心上得到验证且已实用化，本章的例子是其中的一个应用。
由于后处理程序的设计比较复杂，本书没有涉及，如果读者有这方面的需求，可与本书作者联系。
本章以一个实例介绍五轴加工零件的设计方法，产生五轴粗加工和精加工刀具路径的方法和操作步骤，此实例产品为美国一家公司产品的改型件，其特点是应用了环形铣刀全五轴加工，设计的工艺极大地提高了加工效率与加工精度，减小了加工表面粗糙度。
轴测投影图本章简介：本章主要介绍轴侧投影图。
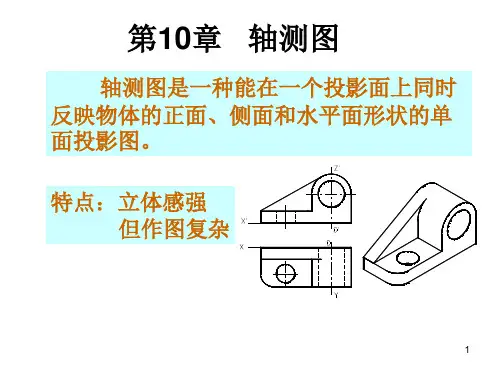
轴测图是一种单面投影图,在一个投影面上能同时反映出物体三个坐标面的形状,并接近于人们的视觉习惯,形象、逼真,富有立体感.但是轴测图一般不能反映出物体各表面的实形,因而度量性差,同时作图较复杂.因此,在工程上常把轴测图作为辅助图样,来说明机器的结构、安装、使用等情况,在设计中,用轴测图帮助构思、想象物体的形状,以弥补正投影图的不足。
本章要求学生了解轴测投影的基本知识，掌握正等侧、斜轴测投影图的画法，具体内容包括轴测投影图的基本知识、正等轴测图、斜轴测图等。
学习重点1. 正等侧、斜轴测的轴间角和轴向伸缩系数2. 正等侧、斜轴测投影图的画法6.1 轴测投影的基本知识图6-1 (a)和图6-1 (b)分别示出同一形体的三面投影图和轴测投影图。
比较这两种图可以看出：三面正投影图既能完整地反映形体的真实形状，又便于标注尺寸，所以在工程中被广泛采用。
但这种图缺乏立体感，需要受过专门训练者才能看懂，而且读图时必须把几个投影图联系起来，才能想象出形体的全貌。
轴测投影图是在一个投影上同时反映形体的长、宽、高三个向度，立体感较强，但度量性较差，作图也较繁琐。
在工程中常采用轴测投影图来弥补多面正投影图直观性差的缺点，故轴测投影图是一种辅助图样。
（a）（b）图6-1 正投影图与轴测投影图（a）三面投影图（b）轴测投影6.1.1 轴测投影图的形成图6-2示出轴测投影图的形成过程。
将形体连同确定其空间位置的直角坐标系，用平行投影法，沿S方向投射到选定的一个投影面P（或Q）上，所得到的投影称为轴测投影。
用这种方法画出的图，称为轴测投影图，简称轴测图。
（a）（b）图6-2 轴测投影图的形成（a）正轴测投影图的形成（b）斜轴测投影图的形成6.1.2 轴间角和轴向伸缩系数如图6-3所示。
当物体连同坐标轴一起投射到轴测投影面（P）上时，坐标轴OX、OY、OZ的投影O1X1、O1Y1、O1Z1称为轴测投影轴。
第10章图样画法复习思考题答案10．1 什么是图样？工程实践中常用的图样有哪些？答：图样是根据投影原理、标准或有关规定，表示工程对象，并有必要的技术说明的图。
工程实践中常用的图样有剖面图、断面图和剖切轴测图等。
10．2 为什么要用剖面图或断面图？答：当物体内部的形状比较复杂时，在投影图中会出现很多虚线，且虚实线相互重叠或交叉，既不易识图，又不便于标注尺寸，且难于表达物体内部材料，此时用剖面图和断面图可以更好的表达物体的内部构造。
10．3 剖面图与断面图分别是怎样形成的？答：剖面图是假想用剖切面剖开物体，移去观察者和剖切面之间的部分，将剩余部分物体向投影面进行正投影所得的图形。
断面图是假想用剖切面剖开物体，将处在观察者与剖切面之间的部分移去，将剖切面与物体相交得到的平面图形称之为断面，仅将该断面向剖切面所平行的投影面投射所得的断面实形即为断面图。
10．4 剖面图中的线型是如何规定的？答：剖面图中的线型规定为：①剖面图中，断面的轮廓线一律用0.7b线宽的实线绘制，断面材料图例线用细实线绘制；其余投影方向可见的部分，一律用0.5b线宽的实线绘制。
②剖面图中一般不画不可见的虚线。
10．5 剖面图与断面图为什么需要标注？剖面图与断面图的投影方向表达方式有什么不同？答：剖面图和断面图的标注是为了看图时便于了解剖切位置和投影方向，寻找投影的对应关系。
剖面图的投影方向采用剖视方向线表达。
断面图的投影方向表达不用剖视方向线而是用断面编号数字的注写位置暗示投射方向，数字在哪一侧，就向那一侧投影10．6剖面图与断面图各分几种类型？各适用于什么对象？答：剖面图的种类及适用对象如下：①全剖面图：当物体需要表达的内部空间单一、简单或对称时；②半剖面图：当物体的内部和外部均需表达，且具有对称平面时，其投影以对称线为界，一半画外形，另一半画成剖面图；③阶梯剖面图：当用一个剖切平面不能将物体需要表达的内部都剖到时，可以将剖切平面直角转折成相互平行的两个或两个以上平行的剖切平面；④旋转剖面图：当用一个剖切平面不能通过物体的各内部结构，而物体在整体上又具有回转轴时，可用两个或两个以上相交的剖切面（剖切面的交线应垂直于某投影面）剖切物体后，将倾斜于投影面的剖面绕其交线旋转展开到与投影面平行的位置形成的剖面图；⑤局部剖面图：对于某些总体形状不太复杂，但有些小的细节需要表达的形体，仅将其需要表达的局部剖开并表示清楚即可的情况；断面图的种类及适用对象如下：根据断面图安放位置不同，一般可分为移出断面图、重合断面图和中断断面图。
第10章轴测图【本章重点】∙轴测图的基本知识∙正等侧∙斜二测轴测图是一种能在一个投影面上同时反映物体的正面、侧面和水平面形状的单面投影图，如图10-1所示，其形象比多面正投影生动，富有立体感，一般人都可以看懂。
但它不能确切地表达机件原来的形状与大小，而且作图较复杂，因此在工程上仅仅作为一种帮助读图的辅助性图样。
图10-1 多面正投影图与轴测图的比较10.1 轴测图的基本知识1.轴测图的形成如图10-2所示，将物体连同其参考直角坐标系，沿不平行于任一坐标面的方向，用平行投影法将其投射在单一投影面上所得的具有立体感的三维图形称为轴测图。
该投影面称为轴测投影面。
根据投射方向与轴测投影面的相对位置，轴测图可分为两大类：∙斜轴测投影图投射方向倾斜于轴测投影面时得到的轴测图，简称斜轴测图，如图10-2（a）所示。
∙正轴测投影图投射方向垂直轴测投影面时得到的轴测图，简称正轴测图，如1第10章 轴测图图10-2（b ）所示。
(a) (b)图10-2 轴测图的形成2. 轴间角及轴向伸缩系数物体的长、宽、高三个方向的坐标轴，即参考直角坐标系的三根坐标轴O 0X 0、O 0Y 0、O 0Z 0在轴测图中的投影OX 、OY 、OZ 称为轴测轴，三条轴测轴的交点称为原点，轴测轴之间的夹角称为轴间角。
轴测轴上的单位长度与相应坐标轴上的单位长度的比值，分别称为X 0、Y 0、Z 0轴的轴向伸缩系数，分别用p 1，q 1，r 1表示。
但在实际作图时，按照实际轴向伸缩系数（可能为小数）计算尺寸非常麻烦，为了便于作图，常采用一组简化伸缩系数p 、q 、r ，使p ：q ：r = p 1：q 1：r 1，简化伸缩系数之比值，即p ：q ：r 应采用简单的数值，简化后的系数称为简化轴向伸缩系数，分别用p 、q 、r 表示。
3. 轴测图的投影特性由于轴测图采用的是平行投影法，由立体几何可知其投影具有如下性质：∙ 立体上两平行线段的轴测投影仍相互平行。
∙ 立体上两平行线段或同一直线上的两线段长度之比值，在轴测图中保持不变。
∙ 立体上平行于轴测投影面的直线和平面，在轴测图上反映实长和实形。
由上述投影性质可知，凡是平行于O 0X 0、O 0Y 0、O 0Z 0轴的线段，其轴测投影仍与相应的轴测轴平行，且具有和X 0、Y 0、Z 0轴相同的轴向伸缩系数。
而不与轴测轴平行的线段，它们的轴向伸缩系数是待求的，作图时不能直接度量。
由此可见，在轴测图中只有沿轴测轴方向测量的长度才与原坐标轴方向的长度有一定的对应关系，轴测投影由此而得名。
；；正等测∙ 三个轴向伸缩系数各不相等的，称为正三测（或斜三测）。
在实际作图时，正等测和斜二测用得较多。
本章只介绍这两种轴测图。
10.2 正等测10.2.1 轴间角和各轴向伸缩系数如图10-3所示，使三个坐标轴与轴测投影面倾斜的角度相同，用正投影法得到的投影图称为正等测。
图10-3 正等测根据理论分析，正等测的轴间角∠XOY ＝∠XOZ ＝∠YOZ ＝120°。
作图时，一般使OZ 轴处于垂直位置，则OX 和OY 轴与水平线成30︒角。
正等测的各轴向伸缩系数均为0.82。
为了作图方便，常采用简化的伸缩系数，即p = q = r = 1，作图时，沿轴向的所有尺寸按实长量取，简捷方便，这样作出的图形与用各轴向伸缩系数0.82画出的轴测图相比较，其形状不变，仅是图形放大了1/0.82≈1.22倍，如图10-4所示。
第10章 轴测图(a) 三视图 (b) 采用轴向伸缩系数 (c) 采用简化轴向伸缩系数图10-4 两种轴向伸缩系数画出的轴测图的比较10.2.2 平面立体正等测图的画法画轴测图的基本方法是坐标法，即根据立体表面上各顶点的坐标值，找出它们的轴测投影，连接各项点，即完成平面立体的轴测图。
在具体作图时，还应根据立体的形状特点，灵活采用各种不同的作图方法。
另外还要注意，轴测图上虚线一般省略不画。
下面举例说明其画法。
【例10-1】 ：作出正六棱柱的正等测，如图10-5所示。
图10-5 正六棱柱的两视图：正等测水平位置的正六边形，为了减少不必要的作图线，坐标原点O 取在顶面的中心，O 0X 0、O 0Y 0、O 0Z 0轴的方向如图10-5所示。
(a) (b) (c) (d)图10-6 作正六棱柱的正等测【作图步骤】：1. 作出轴测轴OX ，OY ，OZ ，如图10-6（a ）所示，在OX 轴上从O 点量取O1=O 010，O4=O 040，同理在OY 轴上求得a 、b 两点。
2. 过a 、b 两点作X 轴的平行线，量取a2=a 020，a3=a 030，同理量取5、6两点，如图10-6(b)所示，依次连接1-2-3-4-5-6-1得到顶面的投影。
3. 由顶面点6，1，2，3作Z 轴的平行线并量取高度，得7，8，9，10，连接7-8-10-10得底面投影，如图10-6(c)所示。
4. 擦去多余线条，加深轮廓线，即完成正六棱柱的正等测，如图10-6(d)所示。
【例10-2】 作出如图10-7所示垫块的正等测图10-7 垫块的三视图 【形体分析，确定坐标轴】：可先画出长方体的正等测，第10章 轴测图为方便作图，坐标体系确定如图10-7所示。
【作图步骤】：1. 作出轴测轴，按尺寸a 、b 、h 画出长方体，如图10-8（a ）所示。
2. 按尺寸c 、d 作出正垂面的轴测投影，如图10-8（b ）所示。
3. 按尺寸e 、f 作出铅垂面的轴测投影，如图10-8（c ）所示。
4.擦去作图线，加深，即得垫块的正等测，如图10-8（d ）所示。
图10-8 作垫块的正等测10.2.3 回转体正等测图的画法10.2.3.1 平行于坐标面的圆的正等测1. 投影分析由正等测的形成可知，各坐标面对轴测投影面都是倾斜的，因此，坐标面或其平行面上相同的，但长短轴方向各不相同。
根据理Z 轴，短轴平行于Z 轴。
各椭圆的长短轴的长度，按轴向伸缩10-9(a)所示；按简化轴向伸缩系数1作图时，如图10-9(b)所示。
为伸缩系数作图。
正等测(a) (b)图10-9 坐标面上圆的正等测2. 近似画法为了简化作图，如图10-9所示中正等测的三个椭圆的作图都可采用近似画法，如图10-10所示在XOY 面上直径为d 的圆，其正等测投影椭圆的画法。
由于这种画法是根据椭圆的外切菱形画出的，因此这种方法也叫菱形四心法。
(a) (b) (c) (d)图10-10 用菱形四心法画平行于XOY 坐标面的圆的正等测【作图步骤】：1. 设立坐标体系，以圆心O 0为坐标原点，两条中心线为坐标轴O 0X 0、O 0Y 0，如图10-10（a ）所示；2. 画轴测轴OX 、OY 。
以圆的直径为边长，作出平行于两根轴测轴的菱形EFGH （即圆外切正方形的轴测投影，该菱形的对角线即为椭圆的长、短轴的位置），如图10-10（b ）所示；3. 菱形两钝角的顶点E 、G 和其两对边中点的连线，与长对角线交于1、2两点，E 、G 、1、2即为四个圆心，如图10-10（c ）所示；4. 分别以E 、G 为圆心，以ED 为半径，画大圆弧和圆弧；以1、2为圆心，以1D 为半径，画小圆弧和弧，即完成作图，如图10.2.3.2 圆柱与圆锥的正等测1. 画圆柱的正等测如图10-11(a)所示，第10章轴测图出顶面的椭圆，然后可用移心法画底面的椭圆，即把顶面椭圆的圆心沿Z轴方向向下移动一个圆柱体的高度，然后画底面椭图，具体作图步骤如图10-11(b)(c)所示。
图10-11 圆柱体的正等测的画法2.画圆锥的正等测如图10-12(a)所示两视图，圆锥正等测的具体画法如图10-12(b)、(c)所示。
图10-12 圆锥正等测的画法(a) 视图(b) 画出顶面的轴测投影后，用移心法画底面的椭圆(c)作两椭圆的公切线（两侧轮廓线），完成全图。
(b) 作顶面的椭圆及底面的菱形四边形(c)作底面的椭圆，作两椭圆的公切线，完成全图正等测3. 圆角的正等测的画法如图10-10所示椭圆的近似画法，可以看出，菱形的钝角与椭圆的大圆弧的画法相同，锐角与椭圆的小圆弧的画法相同；菱形相邻两条边的中垂线的交点就是圆心。
由此可以得出平板上圆角的正等测的近似画法如图10-13(b)、（c ）所示。
图10-13 圆角的正等轴测图画法4. 组合体的正等测图的画法通常可按下列步骤作出组合体的正等测：(1) 对组合体进行形体分析，确定坐标轴。
在确定坐标轴和具体作图时，要考虑作图简便，有利于按坐标关系定位和度量，并尽可能减少作图线。
(2) 作轴测轴，按坐标关系画出物体上的点和线，从而连成物体的正等测。
若物体上有平行于坐标面的圆时，则可按近似画法画出椭圆。
下面举例说明作图步骤。
【例10-3】 ：作出如图10-14所示支架的正等测。
(a)平板的视图 (b)由角顶在两条夹边上量取圆角半径得到切点，过切点作相应边的垂线，交点O 1、O 2即为上底面的两圆心。
用移心法从O 1、O 2向下量取板厚的高度尺寸h ，即得到下底面的对应圆心O 3、O 4(c)以O 1、O 2、 O 3、O 4为圆心，由圆心到切点的距离为半径画圆弧，作两个小圆弧的外公切线，即得两圆角的正等轴测图第10章轴测图图10-14 支架的视图【形体分析，确定坐标轴】：支架由上、下两块板组成，上面一块竖板的顶部是圆柱面，两侧的斜壁与圆柱面相切，中间有一圆柱孔。
下面是一块带圆角的长方形底板，底板的左、右两边都有圆柱形通孔。
因支架左、右对称，取后底边的中点为原点，确定如图10-14所示的坐标体系。
【作图步骤】：如图10-15所示。
图10-15 作支架的正等测10.3 斜二测在斜轴测投影中，若将物体放正，即使XOZ 坐标面平行于轴测投影面，因而XOZ 坐标常用的一种正面斜二测。
(a) 作轴测轴。
先画底板的轮廓，再画竖板与它的交线1234。
确定竖板后孔口的圆心B ，由B 定出前孔口的圆心A ，画出竖板圆柱面顶部的正等测近似椭圆。
(b) 由1、2、3点作切线，再作出右上方（两椭圆弧）的公切线和竖板的圆柱孔，完成竖板的正等测。
由L 1和L 确定底板顶面上两个圆柱孔口的圆心，作出这两个孔的正等测近似椭圆。
(c) 从底板顶面上圆角的切点作切线的垂线，交得圆心C 、D ，再分别在切点间作圆弧，得顶面圆角的正等测。
再作出底面圆角的正等测。
最后，作右边两圆弧的公切线，完成底板的正等测。
(d) 擦去作图线，加深。
10.3.1 斜二测的轴间角和轴向伸缩系数正面斜二测，其轴间角∠XOZ=90︒，∠XOY=∠YOZ=135︒，轴向伸缩系数p= r=1，q =0.5。
如图10-16所示。
作图时，一般使OZ轴处于铅垂位置，则OX轴为水平位置，OY轴与水平线成45︒，通常就将这种正面斜二测简称为斜二测。
