支路电流法

支路电流法名词解释支路电流法是一种电路分析方法，它是基于基尔霍夫电流定律的原理，将电路看做是由许多支路组成的网络，通过计算每个支路内的电流来分析整个电路的性质。

支路电流法常用于求解复杂电路中的电流、电势等问题，下面是支路电流法中常用的一些名词的解释。

1. 支路支路指的是电路中与源端相连的一段电路。

一个支路通常由一个或多个元件（如电阻、电容、电感等）组成，它们按照一定的方式连接在一起，可以形成各种不同的电路结构。

2. 节点节点是指电路中的一个连接点，它可以是电路中一个支路的端点，或者是几个支路的公共连接点。

在支路电流法中，每个节点上会建立一个方程式，用于计算在这个节点上的电流。

3. 回路回路是指电路中的一个闭合环路，它由若干支路按照一定的方式连接在一起形成。

在支路电流法中，每个回路上也会建立一个方程式，用于计算回路的总电势。

4. 支路电流支路电流是指流经一个支路的电流大小。

在支路电流法中，每个支路的电流大小可以通过修正基尔霍夫电流定律，利用欧姆定律和基尔霍夫电压定律得到。

5. 超节点超节点是指连接在电路中两个节点之间的支路中，还有其他元件直接连接在这个支路上的情况。

在支路电流法中，针对这种情况，需要将相邻的节点合并成一个超节点，以简化计算。

6. 方程组方程组是指利用基尔霍夫电流定律和基尔霍夫电压定律等数学原理建立起来的一组方程式。

在支路电流法中，每个节点和每个回路都需要建立一个方程式，通过解这些方程组，得到电路中的各种参数。

总之，支路电流法是一种十分常用的电路分析方法，它可以针对不同的电路结构，通过建立方程组，计算各个支路中的电流大小，从而得到电路的各种性质。

同时，在支路电流法中，需要对各个名词有清晰的定义和理解，才能够正确地应用这种分析方法。

支路电流法说明：这是电工学课程直流电路章节中的一小节，故所用例题均为直流电路。

但支路电路法其实适用于任何电路的分析，是电路分析的基本方法。

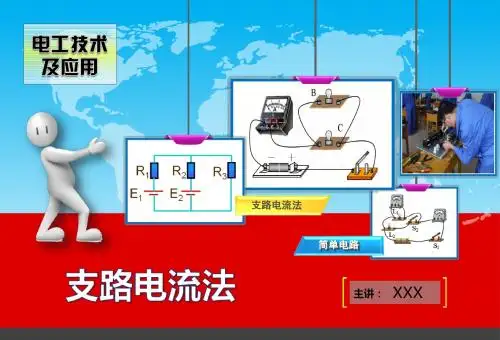
一、引言（问题的引出）图1所示为一简单电路，它有三条支路，如果要求求出这三条支路的电流I 1、I 2、I 3，应该怎么办？(请学生思考并回答。

)图1 图2这个电路可通过欧姆定律及电阻串并联等效化简的方法方便地求解，如果电路变成图2，则又如何求解呢？是否可用同样方法求解呢？答案是否定的。

象这类仅仅用欧姆定律及电阻串并联等效化简的方法不能求解的电路称为复杂电路。

而支路电流法是求解复杂电路的最基本方法之一。

在支路电流法中，除了欧姆定律外，还要用到电路分析中的另一个重要定律：克希荷夫定律（或基尔霍夫定律）。

此时适当复习一下该定律。

二、支路电流法支路电流法：以电路中的支路电流作为待求量，应用基尔霍夫电流定律（KCL ）和基尔霍夫电压定律（KVL ）分别对节点和回路列出所需要的方程电流。

支路电流求出后，其它电量就很容易得到。

下面用支路电流法计算图2电路的电流I 1、I 2、I 3。

1、 为了求解图2电路的3个支路电流I 1、I2、I 3，首先标出各个电流的正方 向，并明确应该列出3个互相独立的方程才能求解。

问题是这三个方程怎么列？2、 用克希荷夫定律列方程(1)先用 KCL 对节点列出方程（称节点电流方程）。

该电路有2个节点，设为A 、B 。

对节点A 有： I 1+I 2-I 3=0 (1) 对节点B 有： -I 1-I 2+I 3=0 (2)显然两式不独立，所以用KVL 可列出1个独立方程，现选（1）式。

一般地，对于有n 个节点的电路，只能列出n-1个独立电流方程。

RR 2 I 2U R2 U(2)然后用KVL 列出所需要的另二个方程（注意是独立方程），称回路电压方程。

选择二个回路，并设定其绕行方向如图所示。

（该电路共有三个回路） 对回路1应用KVL ，得：I 1R 1+I 3R 3-U S 1=0 (3) 对回路2应用KVL ，得：-I 2R 2-I 3R 3+U S 2=0 (4) 若再对回路3列方程：U S 1-I 1R 1+I 2R 2-U S 2=0 (5)很显然，该式是前二式的线性组合，不是独立方程，这样，用KVL 列出了2个相互独立的方程（3）和（4），当然也可以是（4）、（5）或（3）、（5）。

§3.2支路电流法对于一个具有b 条支路和n 个节点的电路，当支路电压和支路电流为电路变量列写方程时，总计有b 2个未知量。

根据KCL 可以列写)1(-n 个独立方程、根据KVL 可以列写)1(+-n b 个独立方程，根据元件的VCR 又可列出b 个方程。

总计方程数为b 2，与未知量数相等。

为了减少求解的方程数，可以利用元件的VCR 将各支路电压以支路电流表示，然后代入KVL 方程，这样，就得到以b 个支路电流为未知量的KCL 方程和KVL 方程。

方程数从b 2减少至b 。

这种方法称为支路电流法。

现以图3-7（a ）所示电路为例说明支路电流法。

把电压源1S u 和电阻1R 的串联组合作为一条支路；把电流源5S i 和电阻5R 的并联组合作为一条支路，这样电路的图就如同图（b ），其节点数4=n ，支路数为6=b ，各支路的方向和编号也示于图中。

求解变量为1i 、2i 、…、n i 。

先利用元件的VCR ，将支路电压1u 、2u 、…、n u 以支路1i 、2i 、…、n i 表示。

图3-7（c ）（d ）给出支路1和支路5的结构，有5SR（a ） （b ）u - 5u +-（c ） （d ）图3-7 支路电流源⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=+====+-=666555554443332221111i R u i R i R u i R u i R u i R u i R u u S S （3-1） 对独立节点①、②、③列出KCL 方程，有⎪⎭⎪⎬⎫=-+-=++-=++-000654432621i i i i i i i i i （3-2）选择网孔作为独立回路，按图3-7（b ）所示回路绕行方向列出KVL 方程⎪⎭⎪⎬⎫=+--=++-=++000642543321u u u u u u u u u （3-3）将式（3-1）代入（3-3），得03322111=+++-i R i R i R u S055554433=+++-S i R i R i R i R0664422=+--i R i R i R把上式中1S u 和55S i R 项移到方程的右边，有⎪⎭⎪⎬⎫=+---=++-=++0664422555544331332211i R i R i R i R i R i R i R u i R i R i R S S （3-4）式（3-2）和式（3-4）就是以支路电流1i 、2i 、…、n i 为未知量的支路电流法方程。