当前位置：文档之家 › 第二章 流体静力学1

第二章 流体静力学1

  • 格式：ppt
  • 大小：6.71 MB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

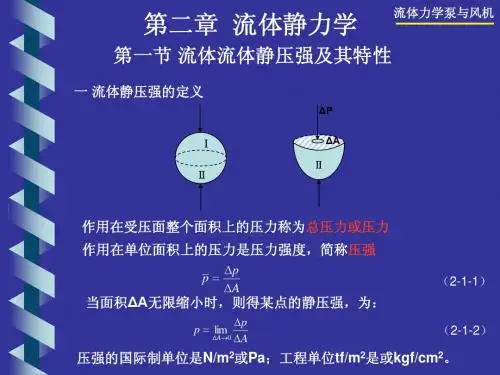
流体力学第二章

流体力学第二章

第一节流体流体静压强及其特性一流体静压强的定义ΔPⅠΔAⅡⅡ作用在受压面整个面积上的压力称为总压力或压力作用在单位面积上的压力是压力强度，简称压强Ap p ∆∆=（2-1-1）App A ∆∆=→∆0lim（2-1-2）当面积ΔA 无限缩小时，则得某点的静压强，为：压强的国际制单位是N/m 2或Pa ；工程单位tf/m 2是或kgf/cm 2。

第一节流体流体静压强及其特性二流体静压强的特性pABCp 1τzxydz dxdyP xP yP nP zdydzp P x x 21⋅=dzdxp P y y 21⋅=dxdyp P z z 21⋅=dAp P n n ⋅=xx f dxdydz F ⋅⋅=61ρyy f dxdydz F ⋅⋅=61ρzz f dxdydz F ⋅⋅=61ρ0)cos(=+∧-x n x F x n P P 061)cos(21=⋅+∧-⋅x n x f dxdydz x n dA p dydz p ρdydzx n dA 21)cos(=∧nx p p =压强方向的假设压强大小计算ΔhΔlΔA第一节流体流体静压强及其特性结论流体静压强的方向与作用面垂直，并指向作用面任意一点各方向的流体静压强大小相等，与作用面的方位无关第二节流体静压强的分布规律p 1p 2Gα0cos 12=⋅--αG P P 0cos 12=∆⋅--αγldA dA p dA p h p p ∆=-γ12hp p γ+=0一液体静压强的基本方程式hp p γ+=12p 0hpph11200z1h2z2z011hppγ+=)(11zzpp-+=γγ/1110zpzp+=+γγ22hppγ+=)(22zzpp-+=γγ/1220zpzp+=+γγCzp=+γ结论：压强水头，压强必须为相对压强位置水头测压管水头,同一容器的静止液体中各点测压管水头相等。

测压管水头表示单位重量流体具有的单位势能。

测压管水头线上的各点，其压强与当地大气压相等。

流体第二章1流体静力学

流体第二章1流体静力学
h
2020/7/6
30
（3）连通容器中盛有两种液体，1 2但液面上的
压强相等（ p01 p02）时，自分界而起，液面的高
度之比与液体容重成反比。
p 0 11 h 1 1 h p 0 22 h 2 1 h
1h12h2
1 h2 2 h1
2020/7/6
31
二、等压面
流体中压力相等的点所组成的面(平面或曲面) 称为等压面（p为常数）。
等压面方程为 d p0X dYxd Z ydz
等压面特性为：
1、dpdU0，U=常量，等压面与等势面重合
2、由等压面方程可知
X Y d Z d ( x X d , Y y , Z ) ( d z , d , d x ) y F z d l 0
2020/7/6
32
2、由等压面方程可知
pB p11gh1 pC p21gh22gh pB pC
p 1 p 2 1 g1 h (1 g2 h2 g)h 1 g (h 1 h 2 )2 g h (21 )g h 读 h 值
如果两球内的压强差微小，为了提高测量精 度常常把压差计的玻璃管倾斜放置，借以达到放 大压差读数提高测量精度。
因此欧拉平衡微分方程为 dp dU
积分可得： pUC
§2-3 流体静压强的基本方程
实际工程中，作用于平衡流体上的质量力只有重力 把z轴取在铅垂方向，则有：
X 0 Y 0 Z g
由欧拉平衡方程，则有
p0, p0, pg
x y z
经积分得出，压力p是 和 z 的函数，即为：
pgzC
p z C(常数） 称为水静力学基本方程
201683135重力场中流体的平衡几何意义不可压缩的重力流体处于平衡状态时静水头线或者计示静水头线为平行于基准面的水平线位置水头压强水头之和为静水头aa静水头线aa计示静水头线26水头与比势能26水头与比势能常数水静力学基本方程201683136物理意义当连续不可压缩的重力流体处于平衡状态时在流体中的任意点上单位重量流体的总势能为常数单位重量流体的位势能单位重量流体的压强势能液体静压强不仅可以用基本公式来计算而且还可以用各种仪表直接测定gh测量办法最简单

第二章 流体静力学

第二章 流体静力学

表面力具有传递性
3
工程流体力学
二、静压力的两个重要特性
• 流体静止时，τ=0；只能承受压应力，即 压强，其方向与作用面垂直，并指向流体 内部。
• 特性1（方向性）：平衡流体中的应力 p⊥→受压面。
• 特性2（大小性）：平衡流体内任一点的压 强p与作用方位无关,即 p =f(x,y,z)。
4
工程流体力学
工程流体力学
第二章 流体静力学
流体静力学是研究流体在静止状态下的 力学规律，包括压强的分布规律和固体壁面 所受到的液体总压力。
1
工程流体力学
第一节 流体静压力及其特性
一、流体静压力：
1、总压力P ：静止流体与容器壁之间、内部相邻 两部分流体之间的作用力。单位“牛”
2、静压力：单位面积上的总压力。即压强。
26
工程流体力学
（1）、测压管
测压管是一种最简单的液柱式测压计。为了减少毛细 现象所造成的误差，采用一根内径为10mm左右的直玻璃 管。测量时，将测压管的下端与装有液体的容器连接，上 端开口与大气相通，如图所示。
测压管只适用于测量较小的压强， 一般不超过19.6MPa，相当于 2mH2O。如果被测压强较高，则 需加长测压管的长度，使用就很不 方便。此外，测压管中的工作介质 就是被测容器中的流体，所以测压 管只能用于测量液体的压强。
例2-6、油罐深度测定，如图所示。已知h1=60cm， △h1=25cm， △h2=30cm，油的相对密度d油=0.9。求h2。
解析：这是由三个以上的容器组成的连通器
1、找出共有等压面。n-n , m-m
2、以A点为计算起点，B点为计算终点，
计算路线如图箭头所示。
3、列连通器平衡方程
n

第二章流体静力学

第二章流体静力学

dy → 0, p y = pS 当四面体向A点收缩时，
同理 px = pz = pS
§2.2静力学基本方程（Euler静平衡方程）：
取一个矩形微元六面体，其六个面分别与 坐标轴平行，设微元中心处的压强为 p。 由于 这是个微小体积，因此认为六个面上的压强各 自均匀分布，常用面上中心来做代表。

而面上中心处的压强又可以围绕六面体 中心做Taylor展开。展开式忽略二阶以上 的高阶量，有
1 ⎞ ⎛ p A = p⎜ x + dx ⎟ 2 ⎠ ⎝
p A = p + 0.5(∂p ∂x )dx
p B = p − 0.5(∂p ∂x )dx

这样，垂直于x轴的两个面上的表面力分 别为
[ p + 0.5(∂p ∂x )dx ]dydz [ p − 0.5(∂p ∂x )dx ]dydz
§2.3重力作用下静止流体内部的压强分布 [均匀液体的压强分布] 根据Euler静平衡方程 可以得到：
p = p0 + γh
第一部分是自由面上的压强，第二部分称 为剩余压强。
p = p0 + γh = γ ( p0 γ + h )
这种做法，称为虚水面方法。
[连通器] （ 1 ）同种液体，表面自由压强相等。则两液面 等高，任一等高度的面上均为等压面。 （ 2 ）同种液体，但表面自由压强不等。则自由 压强大者，液面低。 （3）不同液体（不相混）。密度大者液面低。
F = ∫ ρf dV
V
2、表面力——一个流体体积的表面上，受 到其他部分的流体或与之相接的固体的 作用力。这种力，只是作用在体积的表 面上而没有作用到体积内部的流体质点 上。 通常可以把表面力分解为法向的和 切向的分量，分别称为法向力和切向力。 单位面积上则称为法向应力和切应力。

第二章流体静力学本章研究流体在静止状态下的力学规律。静止：1

第二章流体静力学本章研究流体在静止状态下的力学规律。静止：1

第二章 流体静力学本章研究流体在静止状态下的力学规律。

静止：1、流体整体对于地球没有相对运动的叫绝对静止；2、整体相对于地球有相对运动，而流体各质点没有相对运动，称为相对静止。

第1节、作用在流体上的力作用在流体上的力可分为质量力和表面力两类。

一、质量力：作用在流体的每一个质点上，大小与流体M 成正比，对于均质流体与体积V 也成正比。

最常见两类：重力等由于力场引起的惯性力：直线加速运动：达朗伯尔力曲线运动：离心力单位质量的质量力称为单位质量力，常用它来衡量质量力的大小。

设,,x y F F F z 分别表示质量力F v 在x ，y ，z 三轴上的分量，而用X ，Y ，Z 分别表示单位质量力在三坐标轴上的投影，则x x y y z z F F X M V F F Y M V F F Z M V ρρρ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩设流体只受重力作用，设z 轴铅直向上，则00X Y Mg Z g M⎧⎪=⎪=⎨⎪⎪=−=−⎩ 即单位质量力在数值上就等于加速度，并与加速度量纲相同。

二、表面力：作用在所取流体分离体的表面上的力，并与受作用的流体表面积成比例，单位表面积上的表面力称为应力。

按表面力作用在表面上的方向不同：法向力：与表面法线方向一致切向力：沿表面切线方向作用在上的平均法向应力和平均切向应力分别表示为：SΔ图2-1 作用在流体上的力nn n FP S F SττΔ⎧=⎪⎪Δ⎨Δ⎪=⎪Δ⎩S Δ趋于0（向A 点）并取极限，则可得流体由A 点处的法向应力和切向应力为：lim lim n nS S F dF P S dSF dF S dSτττΔ→∞Δ→∞Δ⎧==⎪⎪Δ⎨Δ⎪==⎪Δ⎩τ是由于流体的粘性和流体具有相对运动而产生的，流体处于静止时，切向应力不再存在，流体表面上就只有法向力，又因流体不能承受拉力，所以法向应力只能指向流体表面的内法线方向，即为流体的静压强。

第二节、流体静压强及其特性流体静压强有两个特性：1、流体静压强的方向垂直于作用面并指向流体内部；2、平衡流体中任意点处的静压强的大小与其作用面的方位无关，只是该点位置坐标的函数，即p=f （x ，y ，z ）。

第二章-流体静力学

第二章-流体静力学

第⼆章-流体静⼒学⼀、学习导引1、流体静⽌的⼀般⽅程（1）流体静⽌微分⽅程x p f x ??=ρ1，y p f y ??=ρ1，zpf z ??=ρ1 （2）压强微分)(dz f dy f dx f dp z y x ++=ρ（3）等压⾯微分⽅程0=++dz f dy f dx f z y x2、液体的压强分布重⼒场中，液体的位置⽔头与压强⽔头之和等于常数，即C pz =+γ如果液⾯的压强为0p ，则液⾯下深度为h 处的压强为h p p γ+=03、固体壁⾯受到的静⽌液体的总压⼒物体受到的⼤⽓压的合⼒为0。

计算静⽌液体对物⾯的总压⼒时，只需考虑⼤⽓压强的作⽤。

（1）平⾯壁总压⼒：A h P c γ= 压⼒中⼼Ay J y y c cc D += 式中，坐标y 从液⾯起算；下标D 表⽰合⼒作⽤点；C 表⽰形⼼。

（2）曲⾯壁总压⼒：222z y x F F F F ++=分⼒：x xc x A h F γ=，y yc y A h F γ=，V F z γ=4、难点分析（1）连通器内不同液体的压强传递流体静⼒学基本⽅程式的两种表达形式为C pz =+γ和h p p γ+=0。

需要注意的是这两个公式只适⽤于同⼀液体，如果连通器⾥⾯由若⼲种液体，则要注意不同液体之间的压强传递关系。

（2）平⾯壁的压⼒中⼼压⼒中⼼的坐标可按式Ay J y y c cc D +=计算，⾯积惯性矩c J 可查表，计算⼀般较为复杂。

求压⼒中⼼的⽬的是求合⼒矩，如果⽤积分法，计算往往还简便些。

（3）复杂曲⾯的压⼒体压⼒体是这样⼀部分空间体积：即以受压曲⾯为底，过受压曲⾯的周界，向相对压强为零的⾯或其延伸⾯引铅垂投影线，并以这种投影线在相对压强为零的⾯或其延伸⾯上的投影⾯为顶所围成的空间体积。

压⼒体内不⼀定有液体。

正确绘制压⼒体，可以很⽅便地算出铅垂⽅向的总压⼒。

（4）旋转容器内液体的相对静⽌液体随容器作等⾓速度旋转时，压强分布及⾃由⾯的⽅程式为c z gr p +-=)2(22ωγc gr z +=2220ω恰当地选取坐标原点，可以使上述表达式简化。

流体力学(流体静力学)


f (x)
f (x0 )
f (x0 )(!
)
(
x
x0
)
2
f
(n) (x0 n!
)
(x
x0
)n
按泰勒级数展开，把M、N点旳静压强写成
p 1
1 p
pM
p [(x dx) x] x 2
p 2
dx x
p 1
1 p
pN
p
[(x x
dx) x] 2
p
2
dx x
其中 p 为压力在x方向旳变化率。因为微元体旳面积取得足够小，
p1 p2
证明：从静止状态旳流体中引入直角坐标系中二维流体微元来
阐明。
设 y 方向宽度为1。ds 即表达任意方向微元表面。
分析 z 方向旳力平衡
表面力：
p1dscosθ=p1dx和p2dx两个力 二维流体微元旳体积：
z
dV 1 dxdz 2
质量力：
p1ds
ds dz x
θ dx
p3dz
y
Fz
1 2
dp ＝ρ1dU dp ＝ρ2dU 因为ρ1≠ρ2 且都不等于零，所以只有当dp和dU均为零时方程 式才干成立。所以其分界面必为等压面或等势面。
§2－4 流体静力学基本方程
重力作用下压力分布 相对平衡液体旳压力分布
§2—4 流体静力学基本方程
一、重力作用下压强分布
如图所示为一开口容器，其中盛有密度为ρ旳静止旳均匀液体 ，液体所受旳质量力只有重力，又ρ＝常数，重度γ＝ρg也为常数。 单位质量力在各坐标轴上旳分量为
（1）
Z 1 p 0
z
上式称为流体平衡微分方程式，它是 Euler在1755年首先提出 旳，故又称欧拉平衡方程式。它表达流体在质量力和表面力作用下 旳平衡条件。

第二讲 流体静力学


p 1 dx dydz pA x 2
,
p 1 dx dydz pA x 2
21
三、平衡微分方程
沿 x 轴方向有 Fx = 0 即：
p 1 p 1 dx dydz p A dx dydz pA x 2 x 2 dxdydz f x 0
化简整理后，将方程两边同除以微小六面体的 质量 dxdydz
22
1 p 得： f x x 0 同理：f 1 p 0 y y 1 p fz 0 z
静止流体的平衡微分方程 (欧拉平衡微分方程）
方程的物理意义 : 在静止流体中，作用在单位质 量流体上的质量力与作用在该流体表面上的压力 相平衡。
—— 重力作用下、连续、均质、不可压缩流体
的静压ቤተ መጻሕፍቲ ባይዱ基本公式（静力学基本方程）。
29
30
二、静压强分布规律 取流体中任意一点 A，考察该点处静压强。
对A点和液面上的一点C列写出静压强基本公式： p0 p z z0 或 gz + p = gz0 + p0 g g 整理得：p = p0 + g( z0 z ) = p0 + gh 静压强分布规律
13
平均流体静压强 p= lim F V 0 A
流体静压力矢量： F= -∫ApdAn
三、 流体静压力的两个重要特性。
1、流体静压力的方向总是沿受作用面法线方向。
2、平衡流体内任一点处的静压强的数值与其作用
面的方向无关，它只是该点空间坐标的函数。
证明：在平衡流体中取出一微小四面体ABOC，考 察其在外力作用下的平衡条件。
p p>pa
表压强 真空度 p<pa

第二章 流体静力学

6
第二节 流体的静压力及其特性
1 1 p x dydz p n An cos(n, x) X dxdydz 0 2 6 1 An cos(n, x) dydz 2
p x pn 1 dydz X 1 dxdydz 0
2 6
1 p x p n X dx 0 6
单位质量力：单位质量流体所受到的质量力。
Fy F Fx Fz f i j k Xi Y j Zk m m m m
设作用在流体上的质量 力只有重力，则：
X=0, Y=0， Z=-mg/m=-g
z
pቤተ መጻሕፍቲ ባይዱ
dz
p
p dy y
o x
dx
dy
y
4
第二节
流体静压力及其特性
•
当流体处于静止或相对静止时，流体单位面 积的表面力称为流体静压强。
三、 静压力的测量
1. 测压管
pA pA
p A pa hA
1
N /m
mH 2O mHg
2
水
1
pa hA pa hA
汞
1 pa hA pA pa标
标准大气压
29
第五节 压力的单位和压力的测量方法
二、 静压力的测量
1. 测压管
p Ag hA
测点处的 z
p
pA /

，所以
zA
pB /
叫测压管水头。
zB
O O
20
流体静力学基本方程的意义
如果容器内的液体是静 止的 ，一根测压管测得 的测压管水头也就是容 器内液体中任何一点的 测压管水头 。 如接上多 根测 压 管， 则各测压管 中的液面都将位于同一 水平面上。

第2章 流体静力学

第2章流体静力学第2章流体静力学第二章静水力学流体静力学主要研究流体在静止状态下的平衡规律及其工程应用。

由于静止状态下流体之间及流体与物面之间的作用是通过静压力的形式来表现的。

所以，本章的中心问题是研究静止状态下静压力的分布规律，进而确定静止流体作用物面上的总压力，用以解决工程实际问题。

静水力学中的静止是指流体粒子之间没有相对运动的状态。

因此，流体静止包括以下两种情况：所谓的绝对静止，即流体作为一个整体与地球没有相对运动；流体作为一个整体对地球有相对运动，但流体粒子之间没有相对运动。

流体静止时，流体质点之间没有相对运动，所以粘滞性在静止流体中显现不出来。

因此，本章所得到的流体平衡规律对理想流体和实际流体均适用。

§2-1静水压力及其特性一、静压力在静止的流体中，没有剪切应力。

因此，流体中的表面力是沿受力表面法向的正压力或法向力。

设在作用微元面积△a上的法向力为△p，则极限δp（2－1）δa?0δa就是流体单位面积上所受到的垂直于该表面的力，即物理学中的压强，称为流体静压力，简称压力，用p表示。

其单位为n/m2，称为帕斯卡，简称帕（pa）。

作用在某一面积上的静压力的合力称为总压力，以p表示，其单位为牛顿（n）。

常用的压力单位有：PA、bar、ATM、mmHg和mh2o。

换算关系为1bar=1×105pa；1atm=1.01325×105pa；1atm=760mmhg；1atm=10.34mh2o；1mmhg=133.28pa；1mh2o=9800pa。

可以看出，静压单位非常小，所以工程实践中常用的单位是kPa（103pa）或MPa（106pa）。

p=lim二、静压力的两个重要特性其中一个特点是：静压遵循作用面内部法线的方向，即它垂直指向作用面。

证明：一方面，流体静止时只有法向力，没有切向力，静压力只能沿法线方向；另一方面，流体不能承受拉力，只能承受压力。

所以，静压力唯一可能的方向就是内法线方向。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、两种平衡状态：绝对平衡和相对平衡 绝对平衡：流体相对于地球无相对运动，即重力场中流体的平衡。 相对平衡：流体对运动容器无相对运动，而对于地球有相对运动。
三、研究思路 流体静压力取决于受压面上各点的静压强，首先研究流体静压 强分布规律、计算与测量，再讨论流体静压力的计算与应用。
§2-1 流体静压强特性
说明：
Ⅰ .无论是否可压、有无粘性均适用
Ⅱ . 反应质量力和表面力的平衡关系，
即质量力与压强变化间的关系，可求p（x，y，z）
例1 . 知重力场中平衡流体（均质不可压）求p=？
解：由于均质不可压， ∴ρ=C
重力场： f x fy 0
fz g
代入单位体积流体欧拉微分方程
p 0 p 0
x
y
p z
平衡状态流层与流层之间无相对运动(du=0)作用在平衡流 体上的表面力只有法向压力研究平衡问题静压强分布规律
特性1：方向必然沿着作用面的内法线方向。（反证法） （静压强作用的垂向性） (举例)
特性2：一点处静压强的大小在各个方向相等。（各向同性） （静压强的各向等值性）(证明如下)
证明：取微元四面体，处于平衡状态
pn pn
0 0
p
z
pn
0
px py pz pn
结论： 作用于平衡流体中任一点上的流体静压强的大小与过该点的作 用面在空间的方向没有关系, 在各个方向上均相等，只与空间位 置坐标有关, 是空间位置坐标的连续函数, 即 p=p (x, y, z)。
§2-2 流体平衡微分方程—欧拉平衡微分方程 目的：求压强分布 p (x, y, z)
dz
综合式：
dp fxdx f ydy fzdz
再解上例
2、质量力势函数
dp fxdx f ydy fzdz
上边在式也保左必守边需力是 是场坐p（中标x, ，函作y数，用的z在）全质的微点全分上微，的分才质，能量p保由力证其所积坐作分标的结唯功果一与的确质唯定点一，所性因经。此过右
dy dxdz
p y
dxdydz
Fz
p
p z
1 2
dz dxdy
p
p z
1 2
dz dxdy
p zBiblioteka dxdydz表面力为F
i
p x
j
p y
k
p z
dxdydz
2、建立平衡条件：
x：
f
x
dxdydz
p x
dxdydz
0
y：
f
y
dxdydz
p y
dxdydz
0
Z:
f
z
dxdydz
p z
dxdydz
0
f
x
p x
0
f
y
p y
0
f z
p z
0
上式称为流体静力学平衡微分方程或Euler平衡微分方程, 数学家 L.Euler 于1775年首次给出。
f
x
p x
0
f
y
p y
0
f z
p z
0
单位体积流体的 Euler平衡微分方程
fx
p x
0
fy
p y
0
fz
p z
0
单位质量流体的 Euler平衡微分方程
f z
g
p gz C
p0 h
z0 z
代入初始条件解得：
p p0 gh
二、欧拉平衡微分方程的积分
1、压强的全微分形式（综合式）
单位质量流体的
fx
p x
0
dx
Euler平衡微分方程
fy
p y
0
dy
fz
p z
0
dz
fxdx
f ydy
f z dz
p x
dx
p y
dy
p z
p左（x，y
1 2
dy，z）
p（x，y，z）
p y
1 2
dy
p右（x，y
1 2
dy，z）
p（x，y，z）
p y
1 2
dy
x方向的表面力为
Fx
p
p x
1 2
dx dydz
p
p x
1 2
dx dydz
p x
dxdydz
同理，y, z 方向的表面力为
Fy
p
p y
1 2
dy dxdz
p
p y
1 2
一、欧拉平衡微分方程 取微元六面体中心点压强为 p = p(x,y,z)。 1、受力分析：质量力（已知）、 表面力（6个）
质量力： F fdxdydz f fxi fy j fzk
表面力： P上、 P 下、P左、 P 右、P前、 P 后
压强 p = p(x,y,z)是坐标的连续函数，按照多元函数泰勒公式：
dp fxdx f ydy fzdz 质量力势函数通常可根据
dp dW
平衡流体所受的单位质量 分力用积分方法加以确定。
该式表明：在有势质量力作用下，流体中任何一点的流体 静压强可以由坐标唯一确定，这样流体才能保持平衡。即： 只有在有势力质量力作用下流体才能平衡。
对不可压缩流体：
p W C, 当：W W0 时， p p0 p p0 (W W0 )
的路径无关, 只与质点的起点、终点位置有关，这样的力称为 有势力，这样的函数称为力函数或势函数。
引入：W =W (x, y, z)——质量力势函数
使 dW fxdx f ydy fzdz
即：
fx
W x
,
fy
W y
,
fz
W z
dW :单位质量 力所作元功
有势质量力
则： dp dW ——质量力为有势力的欧拉平衡微分方程
受力分析：质量力（已知）、表面力（4个）
质量力
f fxi fy j fzk
总质量力
F
fdm
1 dxdydz
6
fxi
fy j
fzk
表面力
Fx
px
1 2
dydz
Fy
py
1 2
dzdx
Fz
pz
1 dxdy 2
Fn pndA
假设ABC与x、y、z方向余弦已知
建立平衡条件：
x：
px
——不可压缩流体欧拉平衡微分方程的积分形式
试确定重力场中平衡流体的的质量力势函数并解释其物理意义。 解：重力场中平衡流体的单位质量力分量为
f x f y 0, f z g
dW W dx W dy W dz
x
y
z
dW fxdx f ydy fzdz
第二章 流体静力学
§2.1 流体静压强及其特性 §2.2 流体平衡微分方程—欧拉平衡微分方程 §2.3 流体静力学基本方程 §2.4 液体的相对平衡 §2.5 作用于平面上的液体总压力 §2.6 作用于曲面上的液体总压力 §2.7 浮力和潜体及浮体的稳定
一、流体静力学研究任务 研究流体处于平衡状态下的力学规律及其在工程中的应用。
1 2
dydz
pndAcosn,
x
1 6
f x dxdydz
0
1 dydz
高阶无穷小量
2
y：
py
1 2
dzdx
pn dA c osn,
y
1 6
f ydxdydz
0
Z:
pz
1 2
dxdy
pn dA c osn,
z
1 6
f z dxdydz
0
当微元四面体体积0, dx, dy, dz0
p p
x y