第一讲地图投影和坐标系统资料

测绘技术中的坐标系和投影方式介绍测绘技术是现代科技的一个重要分支，它涉及到地理空间信息的获取、处理和分析。

而在测绘技术中，坐标系和投影方式是非常重要的概念，它们决定了地理位置的表示和测量的精度。

本文将以深入浅出的方式介绍坐标系和投影方式在测绘技术中的应用。

一、坐标系坐标系是用来表示地点或位置的一种数学概念。

在地球上，利用经纬度坐标系可以描述地球上的各个点的位置。

经度表示东西方向的位置，纬度则表示南北方向的位置。

经度的起点称为本初子午线，通常选取零经度经过英国伦敦的本初子午线。

而纬度的基准线则是赤道。

在坐标系中，经纬度通常以度为单位表示，东经和北纬分别用正值表示，西经和南纬则用负值表示。

这种坐标系在大地测量、地图制作、卫星定位等领域广泛使用，是最基本的测绘坐标系。

除了经纬度坐标系外，还有许多其他坐标系，在不同的应用领域中得到广泛应用。

如笛卡尔坐标系、高程坐标系、地心坐标系等。

这些坐标系根据不同的测绘需求和应用目的而定，为地理空间信息提供了更精确和便捷的表示方式。

二、投影方式在地理空间信息的表达中，一个非常关键的问题是将地球表面上的三维空间映射为平面，这就是投影方式的作用。

由于地球表面是一个椭球体，而平面是一个二维空间，所以无法完美地将地球表面的所有特征映射到平面上。

因此，选择合适的投影方式就显得非常重要。

常见的投影方式包括等角、等积和等距投影等。

等角投影保持地球上两点间的角度关系，适用于海图和飞行导航等领域；等积投影则保持地球上面积的比例，适用于土地管理和资源评价等领域；而等距投影则保持地球上两点间的距离比例，适用于城市规划和测绘制图等领域。

此外，还有许多常用的投影方式，如墨卡托投影、极射投影、兰伯特投影等。

每一种投影方式都有其适用的范围和局限性，根据测绘需求和应用背景的不同，选择合适的投影方式可以使得测绘结果更准确和可用。

三、测绘技术中的应用测绘技术在现代社会中具有广泛的应用，涉及各个领域。

坐标系和投影方式作为测绘技术的重要组成部分，也在种种测绘应用中发挥着重要作用。

测绘技术中的地图投影和坐标系统介绍地图投影和坐标系统是测绘技术中非常重要的内容。

在测绘工作中，我们经常需要将地球上的三维地理空间信息转化为二维的平面地图，这就需要借助地图投影来实现。

同时，为了方便对地球上的各个位置进行准确测量和定位，需要使用坐标系统来进行坐标的表示和计算。

下面，本文将对地图投影和坐标系统进行详细介绍。

1. 地图投影地图投影是将地球上的球面地理信息映射到平面地图上的一种方法。

由于地球是一个球体，而纸张是一个平面，所以无法直接将球面地理信息直接展示在平面地图上。

地图投影的目的就是将地球上的三维地理信息投影到二维的平面地图上，以方便理解和使用。

地图投影有很多种类，常见的有等面积投影、等角投影、等距投影等。

不同的地图投影有各自的优势和适用范围。

等面积投影保持地图上各个区域的面积比例，适用于需要准确表示各个区域大小的地图。

等角投影保持地图上各个区域的角度关系，适用于需要准确表示方向和形状的地图。

等距投影保持地图上各个区域的距离比例，适用于需要准确表示距离和比例的地图。

2. 坐标系统坐标系统是用来表示地球上各个位置坐标的一种体系。

地球是一个球体，所以需要使用三维坐标来表示地球上的点。

常用的地球坐标系统有大地坐标系统和空间直角坐标系统。

大地坐标系统是由经度和纬度组成的坐标系统。

经度表示一个点相对于本初子午线的东西方向的角度，纬度表示一个点相对于赤道的南北方向的角度。

大地坐标系统适用于较小范围内的点的表示和定位。

空间直角坐标系统是由X、Y、Z三个坐标轴组成的坐标系统。

X轴指向地球上的某个固定点，通常是本初子午线上的点；Y轴指向地球上的东方；Z轴垂直于地球的表面向上延伸。

空间直角坐标系统适用于需要较高精度的大范围点的表示和测量。

除了大地坐标和空间直角坐标，还有一些其他的坐标系统，如UTM坐标系统和高程坐标系统等。

它们针对不同的测绘工作和应用领域，提供了不同的坐标表示方式和计算方法。

3. 地图投影与坐标系统的关系地图投影和坐标系统是密不可分的。

地理坐标系统与地图投影的基本知识地理坐标系统（Geographic Coordinate System，简称GCS）是一个基于球体（地球）或椭球体模型的坐标系统，用于描述地球上任意点的位置。

地理坐标系统采用经度和纬度的坐标来确定位置，以度（°）为单位。

经度是从东经0°到西经180°，纬度是从南纬0°到北纬90°。

它们组成了地球的经线和纬线网格，帮助我们定位和导航。

地理坐标系统里最常用的是WGS84坐标系统，也就是全球定位系统（GPS）所采用的坐标系统。

WGS84使用的是地球的平均水准面，被广泛应用于地球科学、地理信息系统和导航系统等领域。

但是需要注意的是，地理坐标系统描述的是在球体或椭球体上的位置，并没有考虑地球表面上的变形。

在制作地图时，我们通常会面临一个问题，即如何把三维的地球表面展开成平面的地图。

这就涉及到地图投影。

地图投影是将球体或椭球体的表面投影到平面上，以便在平面上显示地球的图像。

地图投影有很多种类型，每一种都有其特定的用途和应用。

最常见的地图投影类型之一是等距投影。

等距投影保持了地球上各个点之间的距离比例，即在地图上等距离的两点在地球上也是等距离的。

其中一种常见的等距投影是墨卡托投影，也称为Web墨卡托投影。

墨卡托投影是一种圆柱投影，将地球的经线和纬线投影成直角网格，非常适合用于制作世界地图等大范围的地图。

墨卡托投影最大的特点是保持了地球上各个点之间的角度，但在高纬度地区会出现形变。

除了等距投影外，还有等面积投影、等角投影等不同类型的地图投影。

等面积投影保持了地球上各个区域的面积比例，而等角投影保持了地球上各个点之间的角度比例。

每种投影都有其优点和缺点，根据地图的具体用途和区域选择适合的投影方式很重要。

在实际应用中，我们经常会遇到从一个坐标系统转换到另一个坐标系统的问题。

这需要用到坐标转换方法。

常见的坐标转换方法包括地理转投影，即从地理坐标系统到地图投影的转换，以及地图转地理，即从地图投影到地理坐标系统的转换。

地图的投影、分幅及坐标系前言地质工作者的常规工作是测制各种地质图件。

地质图是在地形图的基础上测制的。

因此，地形图是地质工作者须臾不可离的基础图件。

了解地形图、认识地形图，并能正确使用地形图，是地质工作者的基本技能。

地图一般是由测量专业技术人员测绘、编制的，是一门精深的专业学科。

本人深感对这门知识的缺乏，但又常与地图打交道，也经常遇到一些问题，故积数十年的经历，把一些粗浅认识汇集一起。

本人不是一名测量专业人员，加之知识的浅漏与寡闻，对地图与测量问题，谈之所及不切要害，更是谬误连篇。

初衷不过是借此求教而已。

一地图投影1、地图投影是把三维球面变为二维平面的一种方法地图是根据一定的数学法则将地表的各种现象缩小后用符号表示在平面上的图形。

地表上任意一点的位置都可由经纬度决定，在平面上建立相应的经纬线网，就可以把地表地物相应的转绘到平面图上，这种把三维球面变为二维平面的转绘方法就叫地图投影。

地图投影有多种方法，根据不同的需要，可进行不同的投影常用的地图投影方法有如下几种：（1）、墨卡托投影：在墨卡托投影图上，各部是均等扩张的。

它的面积和长度都是不正确的，但在方向上与地面上的实际方向完全相同，在地图上保持方向的正确是墨卡托投影的最大优点。

故称为“正形投影”，墨卡托投影图常作为航海图和航空图。

（2）、摩尔威特投影在摩尔威特投影图上，中央经线的长度，等于赤道长度的一半，各地的长度变形是很大的。

但各部分的面积保持了正确性，属“等面积投影”，摩尔威特投影图常作为地理现象分布图。

（3）、半球投影类似于从地球之外给地球摄影，所摄部分只有地球的一半，故为半球投影。

优点在于从需要而定投影方位和地区。

（4）、圆锥投影在圆锥投影图上，一个较小的区域其变形程度不大，还可以用数学公式加以修正。

地图册中的许多分国图多用此法绘制。

（5）、高斯——克吕格投影在高斯——克吕格投影图上，长度和面积变形很小，方向也基本不变。

现在的地形图均是以高斯——克吕格投影法绘制的。

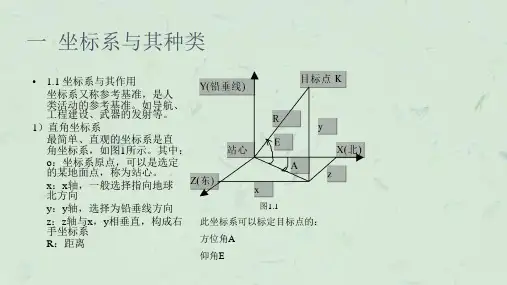
地理坐标与地投影地理坐标系统和地图投影是地理学和地图学中的重要概念。

地理坐标系统用于确定地球上任意位置的准确坐标，而地图投影则是将三维地球表面的地理信息映射到二维平面上的方法。

本文将分别介绍地理坐标系统和地图投影的基本原理和常见方法。

一、地理坐标系统地理坐标系统是用于描述地球上任意位置的坐标系统。

常见的地理坐标系统包括经纬度坐标系统和UTM（通用横轴墨卡托投影）坐标系统。

1. 经纬度坐标系统经纬度坐标系统采用经度和纬度两个角度值来确定地球上的位置。

经度是指位于东西方向上的角度值，以经线为单位，范围为-180度到+180度；纬度是指位于南北方向上的角度值，以纬线为单位，范围为-90度到+90度。

经纬度坐标系统广泛应用于导航、地图制作和地理信息系统等领域。

2. UTM坐标系统UTM坐标系统采用笛卡尔坐标系，将地球表面划分为大小不等的区域，并采用笛卡尔坐标系中的x和y坐标来表示地理位置。

UTM坐标系统通常应用于测绘、地图制作和地理空间分析等工作。

二、地图投影地图投影是将地球表面上的地理信息映射到二维平面上的方法。

由于地球是一个三维球体，将其展示在二维平面上必然存在一定的失真。

1. 球面投影球面投影是将地球表面投影为球面上的图像。

常见的球面投影方法有等面积投影、等角度投影和等距离投影等。

等面积投影保持地球上各个区域的面积比例；等角度投影保持地球上各个区域的角度关系；等距离投影保持地球上各个点之间的距离比例。

2. 平面投影平面投影是将地球表面投影为平面上的图像。

常见的平面投影方法有兰勃托投影、墨卡托投影和极射投影等。

兰勃托投影以一个球面切割成数个相等的楔形区域，然后将楔形区域展开为平面；墨卡托投影通过缩放纬线，使地球表面的纬线等间距分布在投影平面上；极射投影将地球上某一点作为视点，把其他点映射到以该点为中心的圆锥面上。

总结：地理坐标系统和地图投影是地理学和地图学的重要概念。

地理坐标系统通过经纬度坐标或UTM坐标来确定地球上的位置；地图投影是将地球表面的地理信息映射到二维平面上的方法。

地图投影和坐标系统在ArcGIS中，每一个dataset都有一个坐标系统。

它的目的是在一个通用的坐标框架例如map中集成其它地理数据图层。

坐标系统允许你将datasets集成到地图中，同时也做各种各样集成分析的操作，例如叠加不同数据源和坐标系统的图层。

什么是坐标系？坐标系允许地理数据集使用通用的位置来集成。

坐标系是一个参考系统用于代表地理要素的位置，影像以及观测点，例如通用框架下的GPS点。

每一个坐标系统都由以下几部分来定义：（1）它的测量框架要嘛是地理的（球面坐标，从地球中心开始测量）或者是平面的（地理坐标被投影到二维的平面）（2）测量单位（投影坐标一般是feet或者是meters，而球面坐标系一般是经纬度坐标）（3）地图投影的定义是为投影坐标系的（4）其它的测量系统属性，例如大地椭球体，大地水准面以及投影坐标等其它的一个或者多个水平面，中央经线以及可能的X,Y偏移量等。

坐标系统的类型：GIS中一般使用两种通用的坐标系统：（1）球体坐标系，例如经纬度。

这通常称为地理坐标系统。

（2）根据某种地图投影，例如横轴Mercator，Alber等面投影，或者是Robinson投影，投影坐标系统。

所有的这些都提供了各种机制将地球表面投影成二维的平面系。

投影坐标系统一般称为地图投影。

更详细的内容，请参照：地理参考和投影坐标系统投影系统（不论是地理还是投影）提供了定义真实世界坐标的框架。

在ArcGIS中，坐标系统用于自动将其它来显示目录的数据集集成到一个通用的数据集中做投影分析用。

ArcGIS自动集成坐标系统是Known的数据集ArcGIS中所有地理数据集都有一个定义好的坐标生活经验统允许他们在地球表面上定位。

如果你的数据集有一个定义好的坐标系统，那么ArcGIS就会自动将你的数据集跟其它的进行动态投影用于显示，3D可视以及分析等。

如果数据集本身不含有空间参考，那么它们就不能很好地集成。

你需要事先定义它。

什么是ArcGIS中的空间参考？ArcGIS中的空间参考是一系列的参数用于定义投影系统以及其它的空间属性。

地理坐标系与投影坐标系1、地理坐标系（Geographic coordinate system），Geographic coordinate system直译为地理坐标系统，是以经纬度为地图的存储单位的。

很明显，Geographic coordinate system是球面坐标系统。

我们要将地球上的数字化信息存放到球面坐标系统上，如何进行艹作呢？地球是一个不规则的椭球，如何将数据信息以科学的方法存放到椭球上？这必然要求我们找到这样的一个椭球体。

这样的椭球体具有特点：可以量化计算的。

具有长半轴，短半轴，偏心率。

以下几行便是Krasovsky_1940椭球及其相应参数。

Spheroid: Krasovsky_1940Semimajor Axis: 6378245.000000000000000000Semiminor Axis: 6356863.018773047300000000Inverse Flattening（扁率）: 298.300000000000010000然而有了这个椭球体以后还不够，还需要一个大地基准面将这个椭球定位。

在坐标系统描述中，可以看到有这么一行：Datum: D_Beijing_1954表示，大地基准面是D_Beijing_1954。

--------------------------------------------------------------------------------有了Spheroid和Datum两个基本条件，地理坐标系统便可以使用。

完整参数：Alias:Abbreviation:Remarks:Angular Unit: Degree (0.017453292519943299)Prime Meridian（起始经度）: Greenwich (0.000000000000000000) Datum（大地基准面）: D_Beijing_1954Spheroid（参考椭球体）: Krasovsky_1940Semimajor Axis: 6378245.000000000000000000Semiminor Axis: 6356863.018773047300000000Inverse Flattening: 298.3000000000000100002、接下来便是Projection coordinate system（投影坐标系统），首先看看投影坐标系统中的一些参数。