第二讲 最值问题

曲线的参数方程教学目标：1．通过分析抛物运动中时间与运动物体位置的关系，写出抛物运动轨迹的参数方程，体会参数的意义。

2．分析圆的几何性质，选择适当的参数写出它的参数方程。

3．会进行参数方程和普通方程的互化。

教学重点：根据问题的条件引进适当的参数，写出参数方程，体会参数的意义。

参数方程和普通方程的互化。

教学难点：根据几何性质选取恰当的参数，建立曲线的参数方程。

参数方程和普通方程的等价互化。

教学过程一．参数方程的概念1．探究：（1）平抛运动： 为参数）t gt y tx (215001002⎪⎩⎪⎨⎧-== 练习：斜抛运动：为参数）t gt t v y t v x (21sin cos 200⎪⎩⎪⎨⎧-⋅=⋅=αα2．参数方程的概念 （见教科书第22页） 说明：（1）一般来说，参数的变化X 围是有限制的。

（2）参数是联系变量x ，y 的桥梁，可以有实际意义，也可无实际意义。

例1．（教科书第22页例1）已知曲线C 的参数方程是⎩⎨⎧+==1232t y tx (t 为参数) （1）判断点M 1(0,1),M 2(5,4)与曲线C 的位置关系； （2）已知点M 3(6,a )在曲线C 上，求a 的值。

)0,1()21,21()21,31()7,2()(2cos sin 2D C B A y x ，、，、，、的坐标是表示的曲线上的一个点为参数、方程θθθ⎩⎨⎧==A 、一个定点B 、一个椭圆C 、一条抛物线D 、一条直线二．圆的参数方程)(sin cos 为参数t t r y t r x ⎩⎨⎧==ωω)(sin cos 为参数θθθ⎩⎨⎧==r y r x说明：（1）随着选取的参数不同，参数方程形式也有不同，但表示的曲线是相同的。

（2）在建立曲线的参数方程时，要注明参数及参数的取值X 围。

例2．（教科书第24页例2）思考：你能回答教科书第25页的思考吗？三．参数方程和普通方程的互化1．阅读教科书第25页，明确参数方程和普通方程的互化的方法。

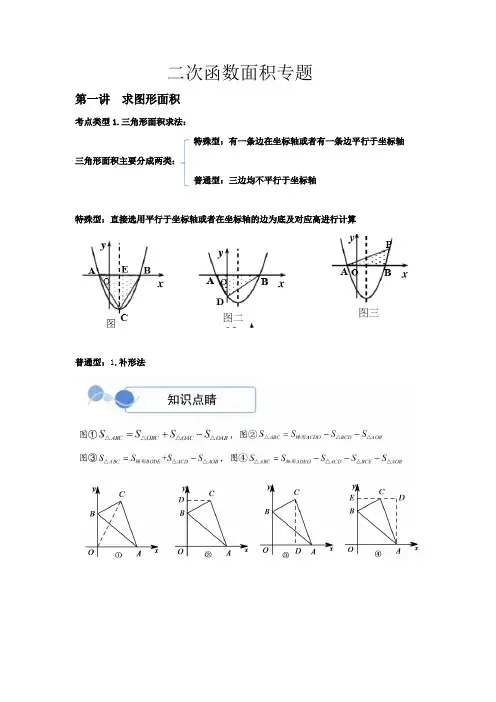
二次函数面积专题第一讲求图形面积
考点类型1.三角形面积求法：
特殊型：直接选用平行于坐标轴或者在坐标轴的边为底及对应高进行计算普通型：1.补形法
2. 割法之铅锤线法：公式：三角形面积=铅锤高×水平宽×2
1 1()2APB B A S PM x x =⋅⋅-△
第二讲 面积最值问题
例1、如图，已知抛物线215222
y x x =-+-，与x 轴交于,A B 两点，交y 轴交于点C ．在直线AC 上方的抛物线上是否存在一点D ，使得DCA ∆的面积最大？若存在，求出点D 的坐标及DCA ∆面积的最大值；若不存在，请说明理由.
-练习：1.如图1，在平面直角坐标系中，直线3944
y x =-+与x 轴交于点A ，与y 轴交于点B ；抛物线2339424
y x x =-++过A ，B 两点，与x 轴交于另一点(1,0)C -，抛物线的顶点为D ，在直线AB 上方的抛物线上有一动点E ，求出点E 到直线AB 的距离的最大值；
小结：三角形面积ABD 最大的时候，F 点坐标有什么特点：
例2、如图，已知二次函数213222
y x x =-
++的图象经过()()()1,04,00,2A B C -、、三点． 点P 是该二次函数图象上位于第一象限上的一动点，连接PA 分别交BC 、y 轴于点E 、F ，若△PEB 、△CEF 的面积分别为S 1、S 2，求S 1﹣S 2的最大值．。

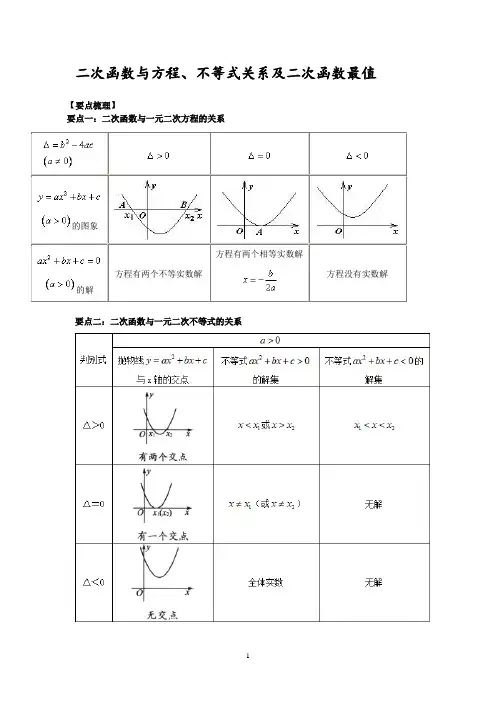
二次函数与方程、不等式关系及二次函数最值【要点梳理】要点一：二次函数与一元二次方程的关系要点二：二次函数与一元二次不等式的关系的图象的解方程有两个相等实数解要点三：二次函数求最值1.对于二次函数的最值问题我们一般转化为其顶点式来解决。

2.对于自变量x 取值范围没有要求的情况，函数的最值在抛物线的顶点处取得；3.对于自变量x 取值范围有特殊要求的，函数的最值需要根据函数此区间的单调性情况来判断；4.抛物线的对称性也是解决函数最值问题的关键。

要点四：二次函数线段、面积最值1. 二次函数与一次函数相结合2. 有线段最值，求面积最值【金题精讲】例1.二次函数的图像与x 轴有2个交点，则k 的取值范围为【变式1】若函数的图像与x 轴有且只有一个交点，在a 的值为_____。

【变式2】二次函数的图像与坐标轴只有两个交点，则c 的值为________。

【变式3】关于的方程有两个相等的实数根，则相应二次函数 与轴必然相交于_______点，此时________。

【变式4】直线1+=x y 与抛物线232++=x x y 的交点的个数为__________ 【变式5】如图，抛物线与直线y=bx+c 的两个交点分别为A(-2,4),B(1,1)，则关于x 的方程的解为___________.)0()a(2≠+-=a k h x y 362+-=x kx y a x x a y 24)1(2+--=32+++=c cx x y x 25mx mx m ++=25y mx mx m =++-x m =2ax y =02=--c bx ax【变式6】已知函数 ，若使y=k 成立的x 的值恰好有3个,则k 的值为_____。

例2.二次函数，当x 满足什么条件时，函数值y 大于0？小于0？【变式1】如图二次函数的图像经过点（-1，0）、（3,0），当y ＞0时，x 的取值范围是（ ）A.x ≤-1或x ≥3B.x ＜-1或x ＞3C.-1＜x ＜3D.-1≤x ≤3【变式2】如图是二次函数的部分图像，由图像可知不等式 ＜0的解集是（ ）A.-1＜x ＜5B.x ＞5C.x ＜-1且x ＞5D.x ＜-1或x ＞5【变式3】二次函数的函数值大于一次函数y=x -1的数值时，求x 的取值范围。

第二讲 多元函数最值和分式函数最值最值问题是高考中出现最广泛,也是最有难度的一类问题,我们解题的根本思路是将要讨论的某个问题的最值用几个变量先表示出来,然后利用题目所给条件,将目标函数转化为单〔主〕变量函数,从而利用导数,均值不等式,三角换元等工具解决函数最值.函数题目中经常有多变量函数,一般都是转化为单变量,一定注意其主元变化X 围,而解析几何中的最值根本都是单变量,主变量X 围一般是：直线与圆锥曲线的位置关系中∆的X 围,方程中变量的X 围,角度的大小等；下面的例子精选出来,希望同学们认真练习,熟悉各种情况下最值问题的处理能力.题型一：二元转化为一元的经典考题例1.,,0a b R x ∈>时,不等式ln ax b x +≥恒成立,如此a b +的最小值？变形：,,0a b R x ∈>时,不等式xax b e +≤恒成立,如此a b +的最大值？例2.函数()f x 满足满足121()(1)(0)2x f x f ef x x -'=-+；〔1〕求()f x 的解析式与单调区间；〔2〕假如21()(1)2f x x a x b ≥+-+,求ab 的最大值. 例3.设函数()()21f x x aIn x =++有两个极值点12x x 、,且12x x <〔I 〕求a 的取值X 围,并讨论()f x 的单调性； 〔II 〕证明：()21224In f x ->例4.函数(1)()ln .1a x f x x x -=-+ 〔Ⅰ〕假如函数()(0,)f x +∞在上为单调增函数,求a 的取值X 围；〔Ⅱ〕设.,n m ，n m >且为正实数求证：2ln ln nm n m n m +<--.例5.直线y a =分别与曲线()21y x =+,ln y x x =+交于A ,B ,如此||AB 的最小值 例6.函数．〔1〕求函数的最大值； 〔2〕假如,不等式恒成立,某某数的取值X 围；〔3〕假如,求证：． 例7.函数21()ln,()22x x f x g x e -=+=,对于,(0,)a R b ∀∈∃∈+∞使得()()g a f b =成立,如此b a -的最小值为〔〕例8.函数f <x >＝22,0,ln ,0,x x a x x x ⎧++<⎨>⎩其中a 是实数．设A <x 1,f <x 1>>,B <x 2,f <x 2>>为该函数图象上的两点,且x 1＜x 2.<1>假如函数f <x >的图象在点A ,B 处的切线互相垂直,且x 2＜0,求x 2－x 1的最小值； <2>假如函数f <x >的图象在点A ,B 处的切线重合,求a 的取值X 围．例9.函数,曲线在点处的切线方程为．〔1〕某某数的值与函数的单调区间；〔2〕假如,求的最大值．题型二：解析几何中分式函数的最值分式函数求最值的主要过程是：先别离,或者换元后凑配别离,一般遵循"照着简单配复杂的〞,即低次换元,高次表示.最后化解为均值不等式模型,或者较为简单的函数形式,然后再去讨论最值,注意化简过程中变量取值X 围的变化.例1：2454x x y x ++=+244xy x x =++228544x x y x x ++=++例2：设F1、F2是椭圆62322=+y x 的两个焦点,AB 是过焦点F1的一条动弦,试求△ABF2面积的最大值,并确定取得最大值时,AB 弦的位置．提示：044)32(22=--+kx x k ,如此324221+-=+k k x x ,, ()ln f x x =()()1g x f x x =+-0x ∀>()21f x ax x ≤≤+a 120x x >>()()1222212122f x f x x x x x x ->-+()xf x e ax =+()y f x =()()0,0f 1y =a ()f x ()()0,1b f x b x c >≥-+2b c 324221+-=k x x yAB F 1 xO222222212212)32()1(483244)324(4)(2++=+-⋅-+-=-+=∴∆k k k k k x x x x S ABF, 令),3[,322+∞∈+=t k t ,3110],41)211([24)1(242222≤<+--=-=∆t t t t SABF , 当t=3时,2ABF S ∆有最大值334,此时k=0,即AB 弦过焦点F1且平行于x 轴．例3〔2014新课标1卷数学〔理〕〕点A 〔0,-2〕,椭圆E ：22221(0)x y a b a b+=>>的离心率为2,F 是椭圆E 的右焦点,直线AF的斜率为3,O 为坐标原点. 〔Ⅰ〕求E 的方程；〔Ⅱ〕设过点A 的动直线l 与E 相交于,P Q 两点,当OPQ ∆的面积最大时,求l 的方程.提示：当 0)34(162>-=∆k ,即432>k 时,143442122+-=⋅=∆k k PQ d S OPQ 设t k =-342,如此0> t ,t t t t S OPQ 44442+=+=∆因为44≥+tt ,当且仅当2=t ,即27±=k 时等号成立,且满足0>∆. 例4〔2013新课标Ⅱ卷〔理〕〕平面直角坐标系中,过椭圆的右焦点作直交于两点,为的中点,且的斜率为.<Ⅰ>求的方程;<Ⅱ>为上的两点,假如四边形的对角线,求四边形面积的最大值.例5：如图,点)1,0(-P 是椭圆)0(1:22221>>=+b a by a x C 的一个顶点,1C 的长轴是圆4:222=+y x C 的直径.21,l l 是过点P 且互相垂直的两条直线,其中1l 交圆2C 于两点,2l 交椭圆1C 于另一点D<1>求椭圆1C 的方程; <2>求ABD ∆面积取最大值时直线1l 的方程.〔2014某某〔理〕〕例6：〔2013某某〕椭圆()2222:10x y C a b a b+=>>,圆()()22222Q x y -+-=的圆心Q在椭圆C 上,点()0,2P 到椭圆C 的右焦点的距离为6．〔I 〕求椭圆C 的方程；〔II 〕过点P 作互相垂直的两条直线12,l l ,且1l 交椭圆C 于,A B 两点, 直线2l 交圆Q 于,C D 两点,且M 为CD 的中点,求MAB ∆的面积的取值X 围．例7：〔2015新课标1卷数学〔理〕〕设圆222150x y x ++-=的圆心为A ,直线l 过点B 〔1,0〕且与x 轴不重合,l 交圆A 于C ,D 两点,过B 作AC 的平行线交AD 于点E .〔I 〕证明EA EB +为定值,并写出点E 的轨迹方程；xOyBl 1l 2 PDA〔第21题图〕〔II 〕设点E 的轨迹为曲线C 1,直线l 交C 1于M ,N 两点,过B 且与l 垂直的直线与圆A 交于P ,Q 两点,求四边形MPNQ 面积的取值X 围.例8一动圆与圆1)1(:221=+-y x O 外切,与圆9)1(:222=++y x O 内切． <I>求动圆圆心M 的轨迹L 的方程．<Ⅱ>设过圆心O 1的直线1:+=my x l 与轨迹L 相交于A 、B 两点,请问2ABO ∆〔O 2为圆O 2 的圆心〕的内切圆N 的面积是否存在最大值？假如存在,求出这个最大值与直线l 的方程,假如不存在,请说明理由．。

第二讲绝对值绝对值是初中代数中的一个基本概念，在求代数式的值、化简代数式、证明恒等式与不等式，以及求解方程与不等式时，经常会遇到含有绝对值符号的问题，同学们要学会根据绝对值的定义来解决这些问题．下面我们先复习一下有关绝对值的基本知识，然后进行例题分析．一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；零的绝对值是零．即绝对值的几何意义可以借助于数轴来认识，它与距离的概念密切相关．在数轴上表示一个数的点离开原点的距离叫这个数的绝对值．结合相反数的概念可知，除零外，绝对值相等的数有两个，它们恰好互为相反数．反之，相反数的绝对值相等也成立．由此还可得到一个常用的结论：任何一个实数的绝对值是非负数．例1 a，b为实数，下列各式对吗？若不对，应附加什么条件？(1)｜a+b｜=｜a｜+｜b｜；(2)｜ab｜=｜a｜｜b｜；(3)｜a-b｜=｜b-a｜；(4)若｜a｜=b，则a=b；(5)若｜a｜＜｜b｜，则a＜b；(6)若a＞b，则｜a｜＞｜b｜．解 (1)不对．当a，b同号或其中一个为0时成立．(2)对．(3)对．(4)不对．当a≥0时成立．(5)不对．当b＞0时成立．(6)不对．当a＋b＞0时成立．例2设有理数a，b，c在数轴上的对应点如图1-1所示，化简｜b-a｜+｜a+c｜+｜c-b｜．解由图1-1可知，a＞0，b＜0，c＜0，且有｜c｜＞｜a｜＞｜b｜＞0．根据有理数加减运算的符号法则，有b-a＜0，a＋c＜0，c-b＜0．再根据绝对值的概念，得｜b-a｜=a-b，｜a+c｜=-(a+c)，｜c-b｜=b-c．于是有原式=(a-b)-(a+c)+(b-c)=a-b-a-c+b-c=-2c．例3已知x＜-3，化简：｜3+｜2-｜1+x｜｜｜．分析这是一个含有多层绝对值符号的问题，可从里往外一层一层地去绝对值符号．解原式=｜3+｜2+(1+x)｜｜(因为1+x＜0)=｜3+｜3+x｜｜=｜3-(3+x)｜(因为3+x＜0)=｜-x｜=-x．解因为 abc≠0，所以a≠0，b≠0，c≠0．(1)当a，b，c均大于零时，原式=3；(2)当a，b，c均小于零时，原式=-3；(3)当a，b，c中有两个大于零，一个小于零时，原式=1；(4)当a，b，c中有两个小于零，一个大于零时，原式=-1．说明本例的解法是采取把a，b，c中大于零与小于零的个数分情况加以解决的，这种解法叫作分类讨论法，它在解决绝对值问题时很常用．例5若｜x｜=3，｜y｜=2，且｜x-y｜=y-x，求x+y的值．解因为｜x-y｜≥0，所以y-x≥0，y≥x．由｜x｜=3，｜y｜=2可知，x＜0，即x=-3．(1)当y=2时，x+y=-1；(2)当y=-2时，x+y=-5．所以x+y的值为-1或-5．例6若a，b，c为整数，且｜a-b｜19+｜c-a｜99=1，试计算｜c-a｜+｜a-b｜+｜b-c｜的值．解 a，b，c均为整数，则a-b，c-a也应为整数，且｜a-b｜19，｜c-a｜99为两个非负整数，和为1，所以只能是｜a-b｜19=0且｜c-a｜99=1，①或｜a-b｜19=1且｜c-a｜99=0．②由①有a=b且c=a±1，于是｜b-c｜=｜c-a｜=1；由②有c=a且a=b ±1，于是｜b-c｜=｜a-b｜=1．无论①或②都有｜b-c｜=1且｜a-b｜+｜c-a｜=1，所以｜c-a｜+｜a-b｜+｜b-c｜=2．解依相反数的意义有｜x-y+3｜=-｜x+y-1999｜．因为任何一个实数的绝对值是非负数，所以必有｜x-y+3｜=0且｜x+y-1999｜=0．即由①有x-y=-3，由②有x+y=1999．②-①得2y=2002， y=1001，所以例8 化简：｜3x+1｜+｜2x-1｜．分析本题是两个绝对值和的问题．解题的关键是如何同时去掉两个绝对值符号．若分别去掉每个绝对值符号，则是很容易的事．例如，化简｜3x+1｜，只要考虑3x+1的正负，即可去掉绝对值符号．这里我们为三个部分(如图1－2所示)，即这样我们就可以分类讨论化简了．原式=-(3x+1)-(2x-1)=5x；原式=(3x+1)-(2x-1)=x+2；原式=(3x+1)+(2x-1)=5x．即说明解这类题目，可先求出使各个绝对值等于零的变数字母的值，即先求出各个分界点，然后在数轴上标出这些分界点，这样就将数轴分成几个部分，根据变数字母的这些取值范围分类讨论化简，这种方法又称为“零点分段法”．例9已知y=｜2x+6｜+｜x-1｜-4｜x+1｜，求y的最大值．分析首先使用“零点分段法”将y化简，然后在各个取值范围内求出y的最大值，再加以比较，从中选出最大者．解有三个分界点：-3，1，-1．(1)当x≤-3时，y=-(2x+6)-(x-1)+4(x+1)=x-1，由于x≤-3，所以y=x-1≤-4，y的最大值是-4．(2)当-3≤x≤-1时，y=(2x+6)-(x-1)+4(x+1)=5x+11，由于-3≤x≤-1，所以-4≤5x+11≤6，y的最大值是6．(3)当-1≤x≤1时，y=(2x+6)-(x-1)-4(x+1)=-3x+3，由于-1≤x≤1，所以0≤-3x+3≤6，y的最大值是6．(4)当x≥1时，y=(2x+6)+(x-1)-4(x+1)=-x+1，由于x≥1，所以1-x≤0，y的最大值是0．综上可知，当x=-1时，y取得最大值为6．例10设a＜b＜c＜d，求｜x-a｜+｜x-b｜+｜x-c｜+｜x-d｜的最小值．分析本题也可用“零点分段法”讨论计算，但比较麻烦．若能利用｜x-a｜，｜x-b｜，｜x-c｜，｜x-d｜的几何意义来解题，将显得更加简捷便利．解设a，b，c，d，x在数轴上的对应点分别为A，B，C，D，X，则｜x-a｜表示线段AX之长，同理，｜x-b｜，｜x-c｜，｜x-d｜分别表示线段BX，CX，DX之长．现要求｜x-a｜，｜x-b｜，｜x-c｜，｜x-d｜之和的值最小，就是要在数轴上找一点X，使该点到A，B，C，D四点距离之和最小．因为a＜b＜c＜d，所以A，B，C，D的排列应如图1－3所示：所以当X在B，C之间时，距离和最小，这个最小值为AD+BC，即(d-a)+(c-b)．例11若2x+｜4-5x｜+｜1-3x｜+4的值恒为常数，求x该满足的条件及此常数的值．分析与解要使原式对任何数x恒为常数，则去掉绝对值符号，化简合并时，必须使含x的项相加为零，即x的系数之和为零．故本题只有2x-5x+3x=0一种情况．因此必须有｜4-5x｜=4-5x且｜1-3x｜=3x-1．故x应满足的条件是此时原式=2x+(4-5x)-(1-3x)+4=7．练习二1．x是什么实数时，下列等式成立：(1)｜(x-2)+(x-4)｜=｜x-2｜+｜x-4｜；(2)｜(7x+6)(3x-5)｜=(7x+6)(3x-5)．2．化简下列各式：(2)｜x+5｜+｜x-7｜+｜x+10｜．3．若a＋b＜0，化简｜a+b-1｜-｜3-a-b｜．4．已知y=｜x+3｜+｜x-2｜-｜3x-9｜，求y的最大值．5．设T=｜x-p｜+｜x-15｜+｜x-p-15｜，其中0＜p＜15，对于满足p ≤x≤15的x来说，T的最小值是多少？6．已知a＜b，求｜x-a｜+｜x-b｜的最小值．7．不相等的有理数a，b，c在数轴上的对应点分别为A，B，C，如果｜a-b｜+｜b-c｜=｜a-c｜，那么B点应为( )．(1)在A，C点的右边；(2)在A，C点的左边；(3)在A，C点之间；(4)以上三种情况都有可能．。

高一第二讲集合与子集在两个集合之间的关系中，我们感兴趣的是“子集”、“真子集”、“相等”这三种特殊关系。

这些关系是通过元素与集合的关系来揭示的，因而判断两个集合之间的关系通常可从判断元素与这两个集合的关系入手。

一子集，相等的集合例 1. 已知集合A={x|x2-3x+2=0}，B={x|x2-ax+a-1=0}, C={x|x2-bx+2=0}, 若Ø，求实数a,b的值⊆,B AC A解因A={1,2}, 且,∅B AØ故b的可能性有三种：,{1},{2}又由于方程x2-ax+a-1=0的根为1和a-1.⊆知，当b=3时,A=C故B只有一种可能a-1=1，即a=2. 由C A-<<.另一种情况是C=∅, 即b2-8<0,b例2. 设集合{}{}==++∈==++∈M u u m n l m n l Z N v v p q r p q r Z1284,,,,201612,..求证：M=N证明：任给x=12m+8n+4l ∈M, 则x=20l+16(n-l)+12(m-n) ∈N, 故M⊆N；任给y=20p+16q+12r ∈N,则y=12r+8(2q)+4(5p) ∈M,故N⊆M.所以M=N.例3. 设函数),( )(2R b a b ax x x f ∈++=，集合}),(|{R x x f x x A ∈==，})],([|{R x x f f x x B ∈==。

（1） 证明：B A ⊆； （2） 当}3,1{-=A 时，求B 。

（3） 当A 只有一个元素时，求证：B A =．解：（1）设任意0x ∈A ，则0x ＝)(0x f .而000)()]([x x f x f f == 故0x ∈B ,所以B A ⊆.(2) 因}3,1{-=A ，所以⎩⎨⎧=+⋅+-=+-⋅+- 3331)1()1(22b a b a 解得3,1-=-=b a故 3)(2--=x x x f 。

第二讲 多元函数最值和分式函数最值最值问题是高考中出现最广泛，也是最有难度的一类问题，我们解题的基本思路是将要讨论的某个问题的最值用几个变量先表示出来，然后利用题目所给已知条件，将目标函数转化为单（主）变量函数，从而利用导数，均值不等式，三角换元等工具解决函数最值。

函数题目中经常有多变量函数，一般都是转化为单变量，一定注意其主元变化范围，而解析几何中的最值基本都是单变量，主变量范围一般是：直线与圆锥曲线的位置关系中∆的范围，方程中变量的范围，角度的大小等；下面的例子精选出来，希望同学们认真练习，熟悉各种情况下最值问题的处理能力。

题型一：二元转化为一元的经典考题例1.已知,,0a b R x ∈>时，不等式ln ax b x +≥恒成立，则a b +的最小值？ 变形：已知,,0a b R x ∈>时，不等式xax b e +≤恒成立，则a b +的最大值？例2.已知函数()f x 满足满足121()(1)(0)2x f x f ef x x -'=-+； （1）求()f x 的解析式及单调区间； （2）若21()(1)2f x x a x b ≥+-+，求ab 的最大值。

例3.设函数()()21f x x aIn x =++有两个极值点12x x 、，且12x x <（I ）求a 的取值范围，并讨论()f x 的单调性；（II ）证明：()21224In f x ->例4.已知函数(1)()ln .1a x f x x x -=-+ （Ⅰ）若函数()(0,)f x +∞在上为单调增函数，求a 的取值范围； （Ⅱ）设.,n m ，n m >且为正实数求证：2ln ln nm n m n m +<--.例5.直线y a =分别与曲线()21y x =+，ln y x x =+交于A ，B ，则||AB 的最小值例6.已知函数．（1）求函数的最大值； （2）若，不等式恒成立，求实数的取值范围；()ln f x x =()()1g x f x x =+-0x ∀>()21f x ax x ≤≤+a（3）若，求证：．例7.已知函数21()ln,()22x x f x g x e -=+=，对于,(0,)a R b ∀∈∃∈+∞使得()()g a f b =成立，则b a -的最小值为（ ）例8.已知函数f (x )＝22,0,ln ,0,x x a x x x ⎧++<⎨>⎩其中a 是实数．设A (x 1，f (x 1))，B (x 2，f (x 2))为该函数图象上的两点，且x 1＜x 2.(1)若函数f (x )的图象在点A ，B 处的切线互相垂直，且x 2＜0，求x 2－x 1的最小值； (2)若函数f (x )的图象在点A ，B 处的切线重合，求a 的取值范围．120x x >>()()1222212122f x f x x x x x x ->-+例9.已知函数,曲线在点处的切线方程为．（1）求实数的值及函数的单调区间；（2）若,求的最大值．题型二：解析几何中分式函数的最值分式函数求最值的主要过程是：先分离，或者换元后凑配分离，一般遵循“照着简单配复杂的”，即低次换元，高次表示。

课堂导学三点剖析一、利用参数方程求点的轨迹 【例1】 已知A 、B分别是椭圆93622y x +=1的左顶点和上顶点,动点C在该椭圆上运动，求△ABC 的重心G 的轨迹的普通方程.解析：本题有两种思考方式，求解时把点C 的坐标设为一般的（x 1，y 1)的形式或根据它在该椭圆上运动也可以设为（6cosθ，3sinθ）的形式，从而予以求解。

解:由动点C 在该椭圆上运动,故据此可设点C 的坐标为（6cosθ，3sinθ）,点G 的坐标为（x ，y)，则由题意可知点A(-6,0）、B （0，3). 由重心坐标公式可知⎪⎪⎩⎪⎪⎨⎧+=++=+-=++-=.sin 13sin 330,cos 223cos 606θθθθy x 由此消去θ得到4)2(2+x +(y —1）2=1，即为所求。

温馨提示本题的解法体现了椭圆的参数方程对于解决相关问题的优越性，运用参数方程显得更简单、更便捷. 各个击破 类题演练 1已知双曲线2222by a x -=1（a>0，b>0）的动弦BC 平行于虚轴，M 、N 是双曲线的左、右顶点。

（1）求直线MB 、CN 的交点P 的轨迹方程；（2）若P （x 1,y 1),B(x 2,y 2),求证：a 是x 1、x 2的比例中项。

（1)解:由题意可设点B(asecθ,btanθ）,则点C(asecθ,-btanθ）,又M(—a ，0),N （a,0)，∴直线MB 的方程为y=aa b +θθsec tan (x+a ），直线CN 的方程为y=θθsec tan a a b -(x-a)。

将以上两式相乘得点P的轨迹方程为2222by a x +=1。

（2）证明：因为P 既在MB 上,又在CN 上，由两直线方程消去y 1得x 1=θsec a,而x 2=asecθ，所以有x 1x 2=a 2,即a 是x 1、x 2的比例中项.变式提升 1在直角坐标系xOy 中,参数方程⎩⎨⎧-=+=12,122t y t x (t 为参数)表示的曲线是___________.解析：t=21-x 代入y=2t 2-1得y=2(21-x )2—1,即（x —1）2=2(y+1).答案：抛物线二、利用参数方程求坐标【例2】 在椭圆7x 2+4y 2=28上求一点，使它到直线l:3x —2y-16=0的距离最短，并求出这一最短距离.解:把椭圆方程化为7422y x +=1的形式，则可设椭圆上点A 坐标为(2cosα，7sinα），则A 到直线l 的距离为d=13|16)sin(8|13|16sin 72cos 6|--=--αβαα（其中β=arcsin 43).∴当β-α=2π时，d 有最小值,最小值为13138138=. 此时α=β—2π，∴sinα=—cosβ=47-,cosα=sinβ=43.∴A 点坐标为（23,47-）。

高三复习第二讲证明不等式的基本方法选修4－5不等式选讲【考纲速读吧】1．了解证明不等式的基本方法：比较法、综合法、分析法、反证法、放缩法．综合法往往是分析法的相反过程，其表述简单、条理清楚．当问题比较复杂时，通常把分析法和综合点必会技巧1．利用基本不等式求最值时，一定要注意“一正二定三相等”，同时还要注意一些变形技巧，积极创造条件利用基本不等式．2．常用的初等变形有均匀裂项、增减项、配系数等．利用基本不等式还可以证明条件不等式，关键是恰当地利用条件，构造基本不等式所需要的形式．项必须注意1．作差比较法适用的主要题型是多项式、分式、对数式、三角式，作商比较法适用的主要题型是高次幂乘积结构．2．放缩法的依据是不等式的传递性，运用放缩法证明不等式时，要注意放缩适度，“放”和“缩”的量的大小是由题目分析，多次尝试得出．放得过大或过小都不能达到证明目的．3．利用柯西不等式求最值，实质上就是利用柯西不等式进行放缩，放缩不当则等号可能不成立，因此，要切记检验等号成立的条件．【课前自主导学】011．三个正数的算术—几何平均不等式a＋b＋c（1）定理：如果a，b，c均为正数，那么________abc，当且仅当________时，等号成立，即3三个正数的算术平均数________它们的几何平均数．（2）基本不等式的推广a1＋a2＋…＋an对于n个正数a1，a2，…，an，它们的算术平均数________它们的几何平均数，即na1a2n，当且仅当________时，等号成立．21（1）已知某>0，则y＝某2＋________．（2）已知某>0，则y＝某的最小值为________．某某2．柯西不等式（1）设a，b，c，d均为实数，则（a2＋b2）（c2＋d2）≥（ac＋bd）2，当且仅当ad＝bc时等号成立．bbb222（2）若ai，bi（i∈N某）为实数，则（∑a）（∑b）≥（∑ab），当且仅当＝＝…＝ai＝0时，iiiia1a2ani＝1i＝1i＝1约定bi＝0，i＝1,2，…，n）时等号成立．（3）柯西不等式的向量形式：设α，β为平面上的两个向量，则|α||β|≥|α·β|，当且仅当α、β共线时等号成立．nnn（1）若某＋2y＋4z＝1，则某2＋y2＋z2的最小值是________．（2）某，y∈R，且某2＋y2＝10，则2某－y的取值范围为________．3．证明不等式的方法（1）比较法①求差比较法由a>ba－b>0，a<ba－b<0，因此要证明a>b，只要证明________即可，这种方法称为求差比较法．②求商比较法a由a>b>0>1且a>0，b>0，因此当a>0，b>0时要证明a>b，只要证明________即可，这种方法称为求商b比较法（2）分析法从所要________入手向使它成立的充分条件反推直至达到已知条件为止，这种证法称为分析法，即“执果索因”的证明方法．（3）综合法从已知条件出发，利用不等式的性质（或已知证明过的不等式），推出所要证明的结论，即“由因寻果”的方法，这种证明不等式的方法称为综合法．（4）反证法的证明步骤第一步：作出与所证不等式________的假设；第二步：从________出发，应用正确的推理方法，推出矛盾的结论，否定假设，从而证明原不等式成立．（5）放缩法所谓放缩法，即要把所证不等式的一边适当地________，以利于化简，并使它与不等式的另一边的不在证明不等式时综合法与分析法有怎样的关系？（1）要证明29＋31<25，可选择的方法最合理的是________．a3＋a6（2）等比数列{an}各项为正数，且q≠1，若PQ＝a4a5，则P与Q的大小关系________．2【自我校对】1．≥a＝b＝c不小于不小于≥a1＝a2＝…＝an31填一填：（1）3（2）34112．填一填：（1提示：∵1＝某＋2y＋4z≤某＋y＋z1＋4＋16，∴某2＋y2＋z2≥某2＋y2＋z2的最2121小值为．21（2）[－2，2]提示：∵（某2＋y2）[22＋（－1）2]≥（2某－y）2，∴－2≤2某－y≤52．a3．a－b>0证明的结论相反条件和假设放大或缩小b想一想：提示：综合法：由条件出发推导出所要证明的不等式成立．分析法：从结论出发寻找使结论成立的充分条件，综合法与分析法是对立统一的两种方法．在实际解题时，常常用分析法探求解题思路，用综合法表达．填一填：（1）分析法（2）P≥Q提示：∵a3·a6＝a4·a5，∴a3＋a6≥23·a6＝2a4·a5，∴P≥Q．【核心要点研究】02【考点一】比较法证明不等式例1[2022·广州模拟]已知a>0，b>0，求证：（a）3＋b3≥ab＋ab2．【审题视点】本题主要考查不等式证明的方法，考查运算求解能力及等价转化思想，可用作差比较法证明．[证明]（a）3＋b3－（ab＋ab2）＝[（a）3－ab]＋[b3－ab2]＝a（a－b）－b2（a－b）＝（a－b）（a－b2a－b）[（a）2－b2]＝（a－b）2（a＋b）．因为a>0，b>0，所以a＋b>0，又（a－b）2≥0，所以（a－b）2a＋b）≥0a）3＋b3－（ab＋ab2）≥0，即（a）3＋b3≥ab＋2．【师说点拨】此题用的是作差比较法，其步骤：作差、变形、判断差的符号、结论．其中判断差的符号为目的，变形是关键．常用的变形技巧有因式分解、配方、拆项、拼项等方法．【变式探究】求证：a2＋b2≥ab＋a＋b－1证明：∵（a2＋b2）－（ab＋a＋b－1）＝a2＋b2－ab－a－b＋1＝2a2＋2b2－2ab－2a－2b＋2）211＝（a2－2ab＋b2）＋（a2－2a＋1）＋（b2－2b＋1）]（a－b）2＋（a－1）2＋（b－1）2]≥0，22∴a2＋b2≥ab＋a＋b－1．【考点二】用分析法或综合法证明不等式1112例2已知a，b，c均为正数，证明：a2＋b2＋c2＋abc3，并确定a，b，c为何值时，等号成立．【审题视点】3因为a，b，c均为正数，且a＋b＋c≥3abc，故可利用三个正数的算术——几何平均不等式证明．2[证明]因为a，b，c均为正数，所以a2＋b2＋c2≥3（abc），①3111211112＋≥9（abc）－．②＋≥3（abcabcabc33111222＋≥3（abc）＋9（abc故a2＋b2＋c2＋abc3322又3（abc）＋9（abc）－≥2＝6，③所以原不等式成立．33当且仅当a＝b＝c时，①式和②式等号成立．221当且仅当3（abc9（abc）－时，③式等号成立．即当且仅当a＝b＝c＝3 334111奇思妙想：例题中，不等式变为“abc3”，其余不变，该如何解答？abc111331113证明：∵a，b，c＋＋abc≥＋abc3，abcabcabcabcabc31∴原不等式成立，当a＝b＝c且abc时等号同时成立，即a＝b＝c＝3 abc6【师说点拨】1．分析法要注意叙述的形式：“要证A，只要证B”，这里B应是A成立的充分条件．2．综合法证明不等式是“由因导果”，分析法证明不等式是“执果索因”．它们是两种思路截然相反的证明方法．分析法便于寻找解题思路，而综合法便于叙述，因此要注意两种方法在解题中的综合运用．【变式探究】设a≥b>0，求证：3a3＋2b3≥3a2b＋2ab2.证明：证法一（综合法）∵a≥b>0，∴a2≥b2，则3a2≥2b2，则3a2－2b2≥0.又a－b≥0，∴(a－b)(3a2－2b2)≥0，即3a3－2ab2－3a2b＋2b3≥0，则3a3＋2b3≥3a2b＋2ab2．故原不等式成立．证法二（分析法）要证3a3＋2b3≥3a2b＋2ab2，只需证3a3＋2b3－3a2b－2ab2≥0，即3a2(a－b)＋2b2(b－a)≥0，也即(a－b)(3a2－2b2)≥0，(某)∵a≥b>0，∴a－b≥0.又a2≥b2，则3a2≥2b2，∴3a2－2b2≥0.(某)式显然成立，故原不等式成立.【考点三】用柯西不等式证明不等式例3[2022·福建高考]已知函数f（某）＝m－|某－2|，m∈R，且f （某＋2）≥0的解集为[－1,1]．111（1）求m的值；（2）若a，b，c∈R＋，且＋＋m，求证：a＋2b＋3c≥9．a2b3c【审题视点】（1）根据式子的特点，利用公式进行转化，根据集合相等确定m的值；（2）结合已知条件构造两个适当的数组，变形为柯西不等式的形式．[解]（1）因为（f某＋2）＝m－|某|，（f某＋2）≥0等价于|某|≤m，由|某|≤m有解，得m≥0，且其解集为{某|－m≤某≤m}．又f（某＋2）≥0的解集为[－1,1]，故m＝1．111＋（2）由（1）知＝1，又a，b，c∈R，由柯西不等式得a2b3c111111a＋2b＋3c＝（a＋2b＋3c）（）≥（a＋2b3c2＝9．所以不等式得证．a2b3ca2b3c【师说点拨】22222柯西不等式的一般结构为（a2（b21＋a2＋…＋an）1＋b2＋…＋bn）≥（a1b1＋a2b2＋…＋anbn），在使用柯西不等式时，关键是将已知条件通过配凑，转化为符合柯西不等式条件的式子，为方便使用柯西不等式，有时常将a变形为1某a的形式．【变式探究】abcbca用柯西不等式证明：若a，b，c均为正数，＋）（）≥9．bcaabcabcbca证明：∵（＋（＋）≥（2＝9，bcaabcbacbacabcbca∴（）＋）≥9．bcaabc【经典演练提能】041．已知a1≤a2，b1≤b2，则P＝a1b1＋a2b2，Q＝a1b2＋a2b1的大小关系是()A．P≤QB．P<QC．P≥QD．P>Q答案：C解析：∵(a1b1＋a2b2)－(a1b2＋a2b1)＝(b1－b2)·(a1－a2)∵a1≤a2，b1≤b2∴(b1－b2)·(a1－a2)≥0∴a1b1＋a2b2≥a1b2＋a2b1．1112．已知a，b，c是正实数，且a＋b＋c＝1＋＋的最小值为（）abcA．3B．6C．9D．12答案：Ca＋b＋ca＋b＋ca＋b＋c111bacacb解析：把a＋b＋c＝1代入＋得到＝3＋（＋＋（＋（＋）≥3 abcabcabacbc＋2＋2＋2＝9，故选C．3.若a，b，c∈(0，＋∞)，且a＋b＋c＝1，则a＋b＋c的最大值为()A.1B.2C.3D.2解析：abc）2＝（a＋b＋c）2≤（12＋12＋12）（a＋b＋c）＝3．当且仅当a＝b＝c＝abc）2≤3．故＋＋的最大值为．3某＋y某y4．设某>0，y>0，M＝N＝M、N的大小关系为________．2＋某＋y2＋某2＋y答案：M<N某＋y某y某y解析：N＝＋>M．2＋某2＋y2＋某＋y2＋某＋y2＋某＋y5．若a，b∈R，且a≠b，M答案：M>N＋ab＋，N＝a＋b，则M、N的大小关系为________．baabab解析：∵a≠bba，ab，baa＋b．baba（时间：45分钟分值：100分）一、选择题1．若|a－c|<|b|，则下列不等式中正确的是（）A．a<b＋cB．a>c－bC．|a|>|b|－|c|D．|a|<|b|＋|c|答案：D解析：|a|－|c|≤|a－c|<|b|，即|a|<|b|＋|c|．故选D．112．[2022·鸡西模拟]若实数某、y＋＝1，则某2＋2y2有（）某yA．最大值3＋22B．最小值3＋2C．最大值6D．最小值6答案：B 112y2某22222解析：由题意知，某＋2y＝（某＋2y）·（＋）＝3＋＋22，某y某y22某2y＝时，等号成立，故选B．y某1113．[2022·广东调研]已知a，b为实数，且a>0，b>0．则（a＋b＋（a2＋）abaA．7B．8C．9D．10答案：C13解析：因为a>0，b>0，所以a＋b＋≥3a某b＝3b>0，①aa113同理可证：a＋＋≥3．②23111321由①②及不等式的性质得（a＋b＋）（a≥3b某9．abab24．[2022·柳州模拟]已知关于某的不等式2某在某∈（a，＋∞）上恒成立，则实数a的最小值为（）某－a13A．B．1CD．222答案：C2223解析：2某＋2（某－a）＋2a≥22某－a2a＝2a＋4≥7，∴a2某－a某－a某－a＋5．[2022·金版原创]若q>0且q≠1，m，n∈N，则1＋qmn与qm＋qn 的大小关系是（）＋＋＋A．1＋qmn>qm＋qnB．1＋qmn<qm＋qnC．1＋qmn＝qm＋qnD．不能确定答案：A解析：1＋qmn－qm－qn＝qm（qn－1）－（qn－1）＝（qn－1）（qm－1），①当0<q<1时，qn<1，qm<1．②当q>1时，qn>1，qm>1．＋∴（qn－1）（qm－1）>0，∴1＋qmn>qm＋qn，故选A．6．[2022·湖北高考]设a，b，c，某，y，z是正数，且a2＋b2＋c2＝10，某2＋y2＋z2＝40，a某＋by＋cz＝20，则a＋b＋c＝（）某＋y＋z1113A．B．C．D．4324答案：C解析：由柯西不等式得（a2＋b2＋c2）（某2＋y2＋z2）≥（a某＋by＋cz）2，而由已知有abc（a2＋b2＋c2）（某2＋y2＋z2）＝10某40＝202＝（a某＋by＋cz）2，故＝＝k，代入得某yza＋b＋c11a2＋b2＋c2＝k2（某2＋y2＋z2）＝40k2＝10，解得k＝k＝．故选C．22某＋y＋z二、填空题7．函数y＝21－某＋2某＋1的最大值为________．答案：3解析：y22－2某＋2某＋1）2≤[（）2＋12][2－2某）22某＋1）2]＝3某3，∴y≤3．8．[2022·许昌模拟]对于任意实数a、b，若|a－b|≤1，|2a－1|≤1，则|4a－3b＋2|的最大值为________．答案：611解析：因为|a－b|≤1，|2a－1|≤1，所以|3a－3b|≤3，|a22151515|4a－3b＋2|＝|（3a－3b）＋（a－|≤|3a－3b|＋|a－|＋≤3＋＋6，即|4a－3b＋2|的最大值为6．2222221119．已知某，y，z为正实数，且＋＝1，则某＋4y＋9z的最小值为________．某yz答案：36解析：解法一：由柯西不等式，得111某＋4y＋9z＝[某）2＋（y）2＋（3z）2]·[（）2＋（22]≥某yz111（某＋y3z）2＝36．当且仅当某＝2y＝3z时等号成立，此时某＝6，y＝3，z＝2．所以当某＝6，y＝3，z＝2时，某＋4y＋9z取得最小值36．111111解法二：∵＋＝1，∴某＋4y＋9z＝（某＋4y＋9z）（＋），某yz某yz4y9z某9z某4y4y某9z某9z4y即某＋4y＋9z＝14＋＋＋≥14＋＋22＝36．某某yyzz某y某zyz（当且仅当某＝2y＝3z时取“＝”），即某＝6，y＝3，z＝2时，（某＋4y＋9z）min＝36．故填36．三、解答题10．已知a>0，证明：a2＋2≥a2．aa1111解：要证a22≥a＋－2，只要证a2＋2≥a＋＋2，因为a>0，所以只要证aaaa1111（a2＋2）2≥（a＋2）2，即证a2＋4＋a2a2＋4＋2（a＋，故只需证aaaaaa1111112a2＋≥a＋，即证a2＋，而由基本不等式可知a2＋成立．故a2－2≥a＋2．211．[2022·正定模拟]设正有理数某是的一个近似值，令y＝1．1＋某（1）若某>3，求证：y3；（2）求证：y比某3．33＋某3某－3某－32证明：（1）y－3＝1＋3＝＝，1＋某1＋某1＋某∵某>3，∴某3>0，而13<0，∴y<3．3－13－2－某3某－（2）∵|y－3|－|某3|＝－|某－3|＝|某－3|（－1）＝|某－3|（，1＋某1＋某1＋某∵某>03－2<0，|某－3|>0，∴|y3|－|某3|<0，即|y－3|<|某3|．∴y比某更接近于3．12．[2022·南昌调研]已知某＋y>0，且某y≠0．某ym11（1）求证：某3＋y3≥某2y＋y2某；（2）如果＋（＋m的取值范围或值．y某2某y解：（1）∵某3＋y3－（某2y＋y2某）＝某2（某－y）－y2（某－y）＝（某＋y）（某－y）2，且某＋y>0，（某－y）2≥0，∴某3＋y3－（某2y＋y2某）≥0．∴某3＋y3≥某2y＋y2某．33某2－某y＋y2某ym11m某＋y（2）（ⅰ）若某y<0，则＋）等价于＝，y某2某y2某y某＋y某y某2－某y＋y2某＋y2－3某y－3某y某3＋y3又∵＝<3，即<－3，∴m>－6；某y某y某y某y某＋y3322某ym11m某＋y某－某y＋y（ⅱ）若某y>0，则≥（＋≤＝，y某2某y2某y某＋y某y某2－某y＋y22某y－某y某3＋y3又∵≥1，即，∴m≤2．某y某y某y某＋y综上所述，实数m的取值范围是（－6,2]．。

26题 第二讲 二次函数参数＋公共点+增减性+极值问题3．在平面直角坐标系xOy 中，直线y=- 56x+m,经过点A （-2，n ）、B （1，12），抛物线y ＝x ²-2tx+t ²-1与x 轴相交于点C 、D.（1）求点A 的坐标（2）设点E 的坐标为（52，0），若点C 、D 都在线段OE 上，求t 的取值范围。

（3）若该抛物线与线段AB 有公共点，求t 的取值范围。

答案：（1）（-2,3）（2）1≤t ≤32 （3）-4≤x ≤-√62+1或0≤x ≤√62+14．已知二次函数y=x²-2ax+a²+2a-3，点A（0,2）、B（1,2）。

（1）二次函数的顶点坐标为_________(用a表示)（2）当二次函数图像与线段AB有公共点时，求a的取值范围（3）若二次函数上有两点（2，y1），（2a-1，y2），当y1＜y2时，求a的取值范围。

二次函数——增减性、极值有关问题。

1、已知抛物线y=-x²+bx+c（b，c为常数）（1）若抛物线交x轴于点A（-1,0）、B（3,0），当-3≤x≤4时，求抛物线上的点到x轴距离的最大值。

（2）若c=b²，当b≤x≤b+3时，抛物线y=-x²+bx+c的最大值为20，求b的值。

2、已知抛物线y=ax²+bx+c（其中a，b，c是常数，a≠0）的对称轴为直线x=-2.（1）填空：b=________（用含a的代数式表示）（2）当a=-1时，若关于x的方程ax²+bx+c=0在-3＜x＜1的范围内有解，求c的取值范围。

（3）若抛物线过点（-2，-2），当-1≤x≤0时，抛物线上的点到x轴距离的最大值为4，求a的值。

作业：3、在平面直角坐标系xOy中，抛物线y=x²-2mx+m²-1与x轴交于A、B两点（点A在点B左侧）。

（1）抛物线顶点坐标_________（用m表示）（2）设抛物线与y轴交于点C（C不与原点o重合），若△AOC的面积始终小于△ABC的面积，求m的取值范围。

第二讲 圆的方程高考中常考题型讲解典例精析题型一 与圆有关的最值问题【例1-1】若实数x ，y 满足(x －2)2＋y 2＝3.求：(1)y x的最大值和最小值； (2)y －x 的最小值；(3)(x －4)2＋(y －3)2的最大值和最小值.【变式训练1-1】已知实数x ，y 满足x 2＋y 2＝3(y ≥0).试求m ＝y ＋1x ＋3及b ＝2x ＋y 的取值范围.【例1-2】求与直线x ＋y －2＝0和曲线x 2＋y 2－12x －12y ＋54＝0都相切的半径最小的圆的标准方程.【变式训练1-2】由直线y ＝x ＋1上的点向圆C ：(x －3)2＋(y ＋2)2＝1引切线，则切线长的最小值为( ) A.17B.3 2C.19D.2 5题型二 圆的方程的应用【例2】在平面直角坐标系xOy 中，二次函数f (x )＝x 2＋2x ＋b (x ∈R )与两坐标轴有三个交点，经过三个交点的圆记为C .(1)求实数b 的取值范围；(2)求圆C 的方程；(3)问圆C 是否经过定点(其坐标与b 无关)？请证明你的结论.【变式训练2】(2010安徽)动点A (x ，y )在圆x 2＋y 2＝1上绕坐标原点沿逆时针方向匀速旋转，12秒旋转一周.已知时间t ＝0时，点A 的坐标是(12，32)，则当0≤t ≤12时，动点A 的纵坐标y 关于t (单位：秒)的函数的单调递增区间是( )A.[0,1]B.[1,7]C.[7,12]D.[0,1]和[7,12]题型三 圆的弦长、中点弦的问题 【例3】已知点P (0,5)及圆C ：x 2＋y 2＋4x －12y ＋24＝0.(1)若直线l 过点P 且被圆C 截得的线段长为43，求l 的方程；(2)求圆C 内过点P 的弦的中点的轨迹方程.【变式训练3】已知圆的方程为x 2＋y 2－6x －8y ＝0，设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为( )A.10 6B.20 6C.30 6D.40 6【例4】设O为坐标原点，曲线x2＋y2＋2x－6y＋1＝0上有两点P、Q关于直线x＋my＋4＝0对称，又满足·OQ＝0.(1)求m的值；(2)求直线PQ的方程.【变式训练4】若曲线x2＋y2＋x－6y＋3＝0上两点P、Q满足①关于直线kx－y＋4＝0对称；②OP⊥OQ，则直线PQ的方程为.总结提高1.解决直线与圆的综合问题时，一方面，我们要注意运用解析几何的基本思想方法(即几何问题代数化)，把它转化为代数问题，通过代数的计算，使问题得到解决；另一方面，由于直线与圆和平面几何联系得非常紧密，因此，我们要勤动手，准确地作出图形，并充分挖掘几何图形中所隐含的条件，利用几何知识使问题较为简捷地得到解决，即注意圆的几何性质的运用.2.解决直线与圆的综合问题时，经常要用到距离，因此两点间的距离公式、点到直线的距离公式要熟练掌握，灵活运用.3.综合运用直线的有关知识解决诸如中心对称、轴对称等一些常见的问题.。

第二讲、二次函数图象及与函数最值【复习要求】1、掌握二次函数解析式的求法2、掌握最值求法【教学重点】熟悉并掌握二次函数求最值的各种题型和方法【教学难点】二次函数求最值【家庭作业】1、完成拓展内容2、复习知识点【知识梳理】1、一般式：y ＝ax 2＋bx ＋c (a ≠0)；顶点式：y ＝a (x ＋h )2＋k (a ≠0)，其中顶点坐标是(－h ，k )．交点式：y ＝a (x －x 1) (x －x 2) (a ≠0)，其中x 1，x 2是二次函数图象与x 轴交点的横坐标． 2、二次函数的图像二次函数y ＝a (x ＋h )2＋k (a ≠0)中，a 决定了二次函数图象的开口大小及方向；h 决定了二次函数图象的左右平移，而且“h 正左移，h 负右移”；k 决定了二次函数图象的上下平移，而且“k 正上移，k 负下移”．（1）当a ＞0时，函数y ＝ax 2＋bx ＋c 图象开口向上；顶点坐标为24(,)24b ac b a a--，对称轴为直线x ＝－2b a ；当x ＜2b a -时，y 随着x 的增大而减小；当x ＞2ba-时，y 随着x的增大而增大；当x ＝2b a-时，函数取最小值y ＝244ac b a -．（2）当a ＜0时，函数y ＝ax 2＋bx ＋c 图象开口向下；顶点坐标为24(,)24b ac b a a--，对称轴为直线x ＝－2b a ；当x ＜2b a -时，y 随着x 的增大而增大；当x ＞2ba-时，y 随着x的增大而减小；当x ＝2b a-时，函数取最大值y ＝244ac b a -．（3）顶点2424b ac b M a a ⎛⎫-- ⎪⎝⎭，． M 在x 轴上方a ⇔∆，异号；在轴下方a ⇔∆，同号；M 在x 轴上0⇔∆=，M在直线y kx t =+上2424kb ac b t a a-⇔+=．（4）图象过点()m n ，，图象过点2()m n am bm c n ⇔++=，，特别地：0m c n =⇔=（为截距）；00m n c ==⇔=；100m n a b c =±=⇔±+=，． 3、二次函数最大值或最小值的求法．第一步确定a 的符号，a ＞0有最小值，a ＜0有最大值； 第二步配方求顶点，顶点的纵坐标即为对应的最大值或最小值． 4、求二次函数在某一范围内的最值．如：2y ax bx c =++在m x n ≤≤（其中m n <）的最值．第一步：先通过配方，求出函数图象的对称轴：0x x =； 第二步：讨论：[1]若0a >时求最小值或0a <时求最大值，需分三种情况讨论： ①对称轴小于m 即0x m <，即对称轴在m x n ≤≤的左侧； ②对称轴0m x n ≤≤，即对称轴在m x n ≤≤的内部； ③对称轴大于n 即0x n >，即对称轴在m x n ≤≤的右侧。

初三数学培优第二讲二次函数的应用一、用二次函数解决最值问题例1 （2006年旅顺口区）已知边长为4的正方形截去一个角后成为五边形ABCDE（如图），其中AF=2，BF=1．试在AB上求一点P，使矩形PNDM有最大面积．解：设矩形PNDM的边DN=x，NP=y，则矩形PNDM的面积S=xy（2≤x≤4）易知CN=4-x，EM=4-y．且有NP BC BFCN AF-=（作辅助线构造相似三角形），即34yx--=12∴y=-12x+5，S=xy=-12x2+5x（2≤x≤4），此二次函数的图象开口向下,对称轴为x=5，∴当x≤5时，•函数的值是随x的增大而增大，对2≤x≤4来说，当x=4时，S有最大值S最大=-12×42+5×4=12．例2 某产品每件成本10元，试销阶段每件产品的销售价x（元）•与产品的日销售量y（件）之间的关系如下表：若日销售量y是销售价x（1）求出日销售量y（件）与销售价x（元）的函数关系式；（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？•此时每日销售利润是多少元？【解析】（1）设此一次函数表达式为y=kx+b．则1525,220k bk b+=⎧⎨+=⎩解得k=-1，b=40，•即一次函数表达式为y=-x+40．（2）设每件产品的销售价应定为x元，所获销售利润为w元w=（x-10）（40-x）=-x2+50x-400=-（x-25）2+225．产品的销售价应定为25元，此时每日获得最大销售利润为225元．例3 （2006年南京市）如图，在矩形ABCD中，AB=2AD，线段EF=10．在EF上取一点M，•分别以EM、MF 为一边作矩形EMNH、矩形MFGN，使矩形MFGN～矩形ABCD．令MN=x，当x为何值时，矩形EMNH的面积S有最大值？最大值是多少？解：∵矩形MFGN∽矩形ABCD，∴MN MF AD AB=，∵AB=2AD，MN=x，∴MF=2x，∴EM=EF-MF=10-2x，∴S=x（10-2x）=-2x2+10x=-2（x-52）2+252，∴当x=52时，S有最大值为252．例4、（2006十堰市）市“健益”超市购进一批20元/千克的绿色食品，如果以30•元/千克销售，那么每天可售出400千克．由销售经验知，每天销售量y（千克）•与销售单价x（元）（x≥30）存在如下图所示的一次函数关系式．（1）试求出y与x的函数关系式；（2）设“健益”超市销售该绿色食品每天获得利润P元，当销售单价为何值时，每天可获得最大利润？最大利润是多少？（3）根据市场调查，该绿色食品每天可获利润不超过4480元，•现该超市经理要求每天利润不得低于4180元，请你帮助该超市确定绿色食品销售单价x的范围（•直接写出答案）．解：（1）设y=kx+b由图象可知，3040020,: 402001000k b kk b b+==-⎧⎧⎨⎨+==⎩⎩解之得，∴y=-20x+1000（30≤x≤50）（2）P=（x-20）y=（x-20）（-20x+1000）=-20x2+1400x-20000．∵a=-20<0，∴P有最大值．当x=-14002(20)⨯-=•35时，P最大值=4500．即当销售单价为35元/千克时，每天可获得最大利润4500元．（3）31≤x•≤34或36≤x≤39．例5、施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米，现在O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）．（1）直接写出点M及抛物线顶点P的坐标；（2）求出这条抛物线的函数解析式；（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下．解：（1）M（12，0），P（6，6）．（2）设这条抛物线的函数解析式为：y=a（x-6）2+6，∵抛物线过O（0，0），∴a（0-6）2+6=0，解得a=16，∴这条抛物线的函数解析式为y=-16（x-6）2+6，即y=-16x2+2x．（3）设点A的坐标为（m，-16m2+2m），∴OB=m，AB=DC=-16m2+2m，根据抛物线的轴对称，可得：OB=CM=m，∴BC=12-2m，即AD=12-2m，∴L=AB+AD+DC=-16m2+2m+12-2m-16m2+2m=-13m2+2m+12=-13（m-3）2+15．∴当m=3，即OB=3米时，三根木杆长度之和L的最大值为15米例6、（2006年泉州市）一条隧道的截面如图所示，它的上部是一个以AD•为直径的半圆O，下部是一个矩形ABCD．（1）当AD=4米时，求隧道截面上部半圆O的面积；（2）已知矩形ABCD相邻两边之和为8米，半圆O的半径为r米．①求隧道截面的面积S（米）关于半径r（米）的函数关系式（不要求写出r的取值范围）；②若2米≤CD≤3米，利用函数图象求隧道截面的面积S的最大值（π取3.14，结果精确到0.1米）（1）当AD=4米时，S半圆=12π×（2AD）2=12π×22=2π（米2）．（2）①∵AD=2r，AD+CD=8，∴CD=8-AD=8-2r，∴S=12πr2+AD·CD=12πr2+2r（8-2r）=（12π-4）r2+16r，②由①知CD=8-2r，又∵2米≤CD≤3米，∴2≤8-2r≤3，∴2．5≤r≤3，由①知S=（12π-4）r2+16r=（12×3.14-4）r2+16r=-2.43r2+16r=-2.43（r-82.43）2+642.43，∵-2.43<0，∴函数图象为开口向下的抛物线，∵函数图象对称轴r=82.43≈3.3．又2.5≤r≤3<3.3，由函数图象知，在对称轴左侧S随r的增大而增大，故当r=3时，S有最大值，S最大值=（12π-4）×32+16×3≈（12×3.14-4）×9+48=26.13≈26.1（米2）．答：隧道截面面积S的最大值约为26.1米2．例7、如图，一块三角形铁片的一边BC=8cm，AH=６cm，在铁片上画一个内接矩形DEFG，使它的边FG 与BC重合，其它两个顶点D和E分别在边AC和AB上，如果设矩形边长EF= x cm, 矩形面积为y2cm。