2017-中考数学-压轴专题-最值问题系列(一)

压轴题1、已知，在平行四边形OABC 中，OA=5，AB=4，∠OCA=90°，动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动，同时动点Q 从A 点出发沿射线AB 方向以每秒1个单位的速度移动．设移动的时间为t 秒． （1）求直线AC 的解析式；（2）试求出当t 为何值时，△OAC 与△PAQ 相似； （3）若⊙P 的半径为58，⊙Q 的半径为23；当⊙P 与对角线AC 相切时，判断⊙Q 与直线AC 、BC 的位置关系，并求出Q 点坐标。

解：（1）42033y x =-+ （2）①当0≤t≤2.5时，P 在OA 上，若∠OAQ=90°时， 故此时△OAC 与△PAQ 不可能相似．当t>2.5时，①若∠APQ=90°，则△APQ ∽△OCA ，∵t>2.5，∴符合条件．②若∠AQP=90°，则△APQ ∽△∠OAC ，∵t>2.5，∴符合条件．综上可知，当时，△OAC 与△APQ 相似．（3）⊙Q 与直线AC 、BC 均相切，Q 点坐标为（109,531）。

2、如图，以矩形OABC 的顶点O 为原点，OA 所在的直线为x 轴，OC 所在的直线为y 轴，建立平面直角坐标系．已知OA ＝3，OC ＝2，点E 是AB 的中点，在OA 上取一点D ，将△BDA 沿BD 翻折，使点A 落在BC 边上的点F 处． （1）直接写出点E 、F 的坐标；（2）设顶点为F 的抛物线交y 轴正半轴．．．于点P ，且以点E 、F 、P 为顶点的三角形是等腰三角形，求该抛物线的解析式；（3）在x 轴、y 轴上是否分别存在点M 、N ，使得四边形MNFE 的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．解：（1）(31)E ，；(12)F ，．（2）在Rt EBF △中，90B ∠=o， 2222125EF EB BF ∴=+=+=．设点P 的坐标为(0)n ，，其中0n >，Q 顶点(12)F ，， ∴设抛物线解析式为2(1)2(0)y a x a =-+≠．①如图①，当EF PF =时，22EF PF =，221(2)5n ∴+-=．解得10n =（舍去）；24n =．(04)P ∴，．24(01)2a ∴=-+．解得2a =． ∴抛物线的解析式为22(1)2y x =-+（第2题）②如图②，当EP FP =时，22EP FP =，22(2)1(1)9n n ∴-+=-+． 解得52n =-（舍去）．③当EF EP =时，53EP =<，这种情况不存在． 综上所述，符合条件的抛物线解析式是22(1)2y x =-+． （3）存在点M N ，，使得四边形MNFE 的周长最小． 如图③，作点E 关于x 轴的对称点E '，作点F 关于y 轴的对称点F '，连接E F ''，分别与x 轴、y 轴交于点M N ，，则点M N ，就是所求点．(31)E '∴-，，(12)F NF NF ME ME '''-==，，，．43BF BE ''∴==，．FN NM ME F N NM ME F E ''''∴++=++=22345+=．又5EF =Q ，∴55FN NM ME EF +++=+，此时四边形MNFE 的周长最小值是553、如图，在边长为2的等边△ABC 中，A D ⊥BC,点P 为边AB 上一个动点，过P 点作PF//AC 交线段BD 于点F,作PG ⊥AB 交AD 于点E,交线段CD 于点G,设BP=x . （1）①试判断BG 与2BP 的大小关系,并说明理由;②用x 的代数式表示线段DG 的长,并写出自变量x 的取值范围;（2）记△DEF 的面积为S,求S 与x 之间的函数关系式,并求出S 的最大值;（3）以P 、E 、F 为顶点的三角形与△EDG 是否可能相似？如果能相似，请求出BP 的长，如果不能，请说明理由。

专题10二次函数与线段最值定值及数量关系问题图形运动的过程中，求两条线段之间的函数关系，是中考数学的热点问题．产生两条线段间的函数关系，常见的情况有两种，一是勾股定理，二是比例关系．还有一种不常见的，就是线段全长等于部分线段之和．由比例线段产生的函数关系问题，在两种类型的题目中比较常用．一是由平行线产生的对于线段成比例，二是相似三角形的对应边成比例．一般步骤是先说理产生比例关系，再代入数值或表示数的字母，最后整理、变形，根据要求写出定义域．关键是寻找比例关系，难点是有的整理、变形比较繁琐，容易出错．【例1】（2021•沈阳）如图，平面直角坐标系中，O是坐标原点，抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点B坐标是（3，0）．抛物线与y轴交于点C（0，3），点P是抛物线的顶点，连接PC．（1）求抛物线的函数表达式并直接写出顶点P的坐标．（2）直线BC与抛物线对称轴交于点D，点Q为直线BC上一动点．①当△QAB的面积等于△PCD面积的2倍时，求点Q的坐标；②在①的条件下，当点Q在x轴上方时，过点Q作直线l垂直于AQ，直线y＝x﹣交直线l于点F，点G在直线y＝x﹣上，且AG＝AQ时，请直接写出GF的长．【例2】（2021•滨州）如下列图形所示，在平面直角坐标系中，一个三角板的直角顶点与原点O重合，在其绕原点O旋转的过程中，两直角边所在直线分别与抛物线y＝x2相交于点A、B（点A在点B的左侧）．（1）如图1，若点A、B的横坐标分别为﹣3、，求线段AB中点P的坐标；（2）如图2，若点B的横坐标为4，求线段AB中点P的坐标；（3）如图3，若线段AB中点P的坐标为（x，y），求y关于x的函数解析式；（4）若线段AB中点P的纵坐标为6，求线段AB的长．【例3】（2021•盘锦）如图，抛物线y＝﹣x2+2x+6与x轴交于A，B两点（点A在点B的左侧），与y 轴交于点C，直线y＝x﹣2与y轴交于点D，与x轴交于点E，与直线BC交于点F．（1）点F的坐标为；（2）如图1，点P为第一象限抛物线上的一点，PF的延长线交OB于点Q，PM⊥BC于点M，QN⊥BC于点N，若＝，求点P的坐标；（3）如图2，点S为第一象限抛物线上的一点，且点S在射线DE上方，动点G从点E出发，沿射线DE方向以每秒4个单位长度的速度运动，当SE＝SG，且tan∠SEG＝时，求点G的运动时间t．【例4】（2021•巴中）已知抛物线y＝ax2+bx+c与x轴交于A（﹣2，0）、B（6，0）两点，与y轴交于点C （0，﹣3）．（1）求抛物线的表达式；（2）点P在直线BC下方的抛物线上，连接AP交BC于点M，当最大时，求点P的坐标及的最大值；（3）在（2）的条件下，过点P作x轴的垂线l，在l上是否存在点D，使△BCD是直角三角形，若存在，请直接写出点D的坐标；若不存在，请说明理由．【例5】（2020•孝感）在平面直角坐标系中，已知抛物线y＝ax2+4ax+4a﹣6（a＞0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．（1）当a＝6时，直接写出点A，B，C，D的坐标：A，B，C，D；（2）如图1，直线DC交x轴于点E，若tan∠AED=43，求a的值和CE的长；（3）如图2，在（2）的条件下，若点N为OC的中点，动点P在第三象限的抛物线上，过点P作x 轴的垂线，垂足为Q，交AN于点F；过点F作FH⊥DE，垂足为H．设点P的横坐标为t，记f＝FP+FH．①用含t的代数式表示f；②设﹣5＜t≤m（m＜0），求f的最大值．【例6】（2020•恩施州）如图1，抛物线y=−14x2+bx+c经过点C（6，0），顶点为B，对称轴x＝2与x轴相交于点A，D为线段BC的中点．（1）求抛物线的解析式；（2）P为线段BC上任意一点，M为x轴上一动点，连接MP，以点M为中心，将△MPC逆时针旋转90°，记点P的对应点为E，点C的对应点为F．当直线EF与抛物线y=−14x2+bx+c只有一个交点时，求点M的坐标．（3）△MPC在（2）的旋转变换下，若PC=2（如图2）．①求证：EA＝ED．②当点E在（1）所求的抛物线上时，求线段CM的长．【题组一】1．（2021•青山区模拟）已知抛物线y＝ax2﹣4ax﹣12a与x轴相交于A，B两点，与y轴交于C点，且OC ＝OA．设抛物线的顶点为M，对称轴交x轴于点N．（1）求抛物线的解析式；（2）如图1，点E（m，n）为抛物线上的一点，且0＜m＜6，连接AE，交对称轴于点P．点F为线段BC上一动点，连接EF，当PA＝2PE时，求EF+BF的最小值．（3）如图2，过点M作MQ⊥CM，交x轴于点Q，将线段CQ向上平移t个单位长度，使得线段CQ 与抛物线有两个交点，求t的取值范围．2．（2021•赣州模拟）已知抛物线C1：y＝x2﹣4x+3m和C2：y＝mx2﹣4mx+3m，其中m≠0且m≠1．（1）抛物线C1的对称轴是，抛物线C2的对称轴是；（2）这两条抛物线相交于点E，F（点E在点F的左侧），求E、F两点的坐标（用含m的代数式表示）并直接写出直线EF与x轴的位置关系；（3）设抛物线C1的顶点为M，C2的顶点为N；①当m为何值时，点M与点N关于直线EF对称？②是否存在实数m，使得MN＝2EF？若存在，直接写出实数m的值，若不存在，请说明理由．3．（2021•桓台县二模）在平面直角坐标系中，抛物线y＝x2+bx+c交x轴于A，B两点，点A，B的坐标分别为（﹣1，0），（3，0），点M为顶点．（1）求抛物线的解析式；（2）过点M作y轴的垂线，垂足为C，过点B作y轴的平行线，交CM于点D，点H为OC上的任一点，将线段HB绕点H逆时针旋转90°到HP．求∠PCD的度数；（3）在（2）的条件下，将点H改为y轴上的一动点，连接OP，BP，求OP+BP的最小值．4．（2021•成都模拟）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式．（2）点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G，H，设点D的横坐标为m．①求DF+HF的最大值；②连接EG，若∠GEH＝45°，求m的值．【题组二】5．（2021•攸县模拟）材料：对抛物线，定义：点叫做该抛物线的焦点，直线叫做该抛物线的准线，且该抛物线上任意一点到焦点的距离与它到准线的距离相等．运用上述材料解决如下问题：如图所示，已知抛物线C：y＝ax2﹣4ax的图象与x轴交于O、A两点，且过点．（1）求抛物线C的解析式和点A的坐标；（2）若将抛物线C的图象先向左平移2个单位，再向上平移1个单位得到抛物线C'的图象．①求抛物线C'的焦点坐标和准线方程．②设M为抛物线C'位于第一象限内图象上的任意一点，MN⊥x轴于点N，求MN+MA的最小值，并求出取得这个最小值时点M的坐标．6．（2021•南沙区一模）已知，抛物线y＝mx2+x﹣4m与x轴交于点A（﹣4，0）和点B，与y轴交于点C．点D（n，0）为x轴上一动点，且有﹣4＜n＜0，过点D作直线l⊥x轴，且与直线AC交于点M，与抛物线交于点N，过点N作NP⊥AC于点P．点E在第三象限内，且有OE＝OD．（1）求m的值和直线AC的解析式．（2）若点D在运动过程中，AD+CD取得最小值时，求此时n的值．（3）若△ADM的周长与△MNP的周长的比为5：6时，求AE+CE的最小值．7．（2021•宝安区模拟）（1）已知二次函数经过点A（﹣3，0）、B（1，0）、C（0，3），请求该抛物线解析式；（2）点M为抛物线上第二象限内一动点，BM交y轴于点N，当BM将四边形ABCM的面积分为1：2两部分时，求点M的坐标；（3）点P为对称轴上D点下方一动点，点Q为直线y＝x第一象限上的动点，且DP＝OQ，求BP+BQ 的最小值并求此时点P的坐标．8．（2021•茶陵县模拟）如图，在平面直角坐标系中，抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（﹣1，0）、B（3，0），与y轴交于点C，点P是直线BC上方抛物线上的动点．（1）求抛物线的解析式；（2）如图①，连接BC与OP，交于点D，求当的值最大时点P的坐标；（3）如图②，过点P作PD∥AC交x轴于点D，交BC于点E，求BE的最大值及点P的坐标．【题组三】9．（2021•东莞市校级一模）如图，抛物线y＝ax2+bx+3与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于C点，抛物线的对称轴l与x轴交于M点．（1）求抛物线的函数解析式；（2）设点P是直线l上的一个动点，当PA+PC的值最小时，求PA+PC长；（3）已知点N（0，﹣1），在y轴上是否存在点Q，使以M、N、Q为顶点的三角形与△BCM相似？若存在，请求出点Q的坐标；若不存在，请说明理由．10．（2021•怀化模拟）如图，已知抛物线y＝ax2+bx+3的对称轴是直线x＝1，与x轴交于点A、B，与y 轴交于点C，其中点A的坐标是（﹣1，0）．（1）直接写出点B的坐标并求出抛物线的解析式；（2）点P是抛物线上的一个动点．①当∠PCB＝∠OCB时，求点P的坐标；②当点P在B、C两点之间运动时，连接AP，交BC于点Q，设t＝，求当t值最大时点P的坐标．11．（2021•罗湖区三模）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）直接写出抛物线的解析式：；（2）点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H，设点D的横坐标为m．①求DF+HF的最大值；②连接EG，若∠GEH＝45°时，求m的值．12．（2021•南海区二模）如图1，抛物线y＝x2+bx+c与x轴交于A、B两点，点A、B分别位于原点左、右两侧，且AO＝2BO＝4，过A点的直线y＝kx+c交y轴于点C．（1）求k、b、c的值；（2）在抛物线的对称轴上是否存在一点P，使△ACP为直角三角形？若存在，直接写出所有满足条件的点的坐标；若不存在，请说明理由；（3）如图2，点M为线段AC上一点，连接OM，求AM+OM的最小值．【题组四】13．（2020•西宁二模）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+c与x轴交于A（5，0），B（﹣1，0）两点，与y轴交于点C（0，52）．（1）求抛物线的解析式；（2）若点M是抛物线的顶点，连接AM，CM，求△AMC的面积；（3）若点P是抛物线上的一个动点，过点P作PE垂直y轴于点E，交直线AC于点D，过点D作x 轴的垂线，垂足为点F，连接EF，当线段EF的长度最短时，求出点P的坐标．14．（2020•涡阳县一模）如图，抛物线y＝ax2+bx+c（a≠0）与直线y＝x+1相交于A（﹣1，0），B（4，m）两点，且抛物线经过点C（5，0）．（1）求抛物线的解析式．（2）点P是直线上方的抛物线上的一个动点，求△ABP的面积最大时的P点坐标．（3）若点P是抛物线上的一个动点（不与点A点B重合），过点P作直线PD⊥x轴于点D，交直线AB 于点E．当PE＝2ED时，求P点坐标；（4）设抛物线与y轴交于点F，在抛物线的第一象限内，是否存在一点M，使得AM被FC平分？若存在，请求出点M的坐标；若不存在，说明理由．15．（2020•哈尔滨模拟）如图，抛物线y＝ax2+bx+5经过坐标轴上A、B和C三点，连接AC，tan C=355OA＝3OB．（1）求抛物线的解析式；（2）点Q在第四象限的抛物线上且横坐标为t，连接BQ交y轴于点E，连接CQ、CB，△BCQ的面积为S，求S与t的函数解析式；（3）已知点D是抛物线的顶点，连接CQ，DH所在直线是抛物线的对称轴，连接QH，若∠BQC＝45°，HR∥x轴交抛物线于点R，HQ＝HR，求点R的坐标．16．（2020•皇姑区校级一模）如图，在平面直角坐标系中，抛物线y=−12x2+bx+c与x轴交于点A，B，其中点B的坐标为（4，0），与y轴交于点C（0，2）．（1）求抛物线y=−122+bx+c和直线BC的函数表达式；（2）点P是直线BC上方的抛物线上一个动点，当点P到直线BC的距离最大时，求点P的坐标；（3）连接点O与（2）中求出的点P，交直线BC于点D，点N是直线BC上的一个动点，连接ON，作DF⊥ON于点F，点F在线段ON上，当OD=5DF时，请直接写出点N的坐标．【题组五】17．（2020•岳阳二模）如图，已知抛物线y＝x2+bx+c与x轴相交于A（﹣1，0），B（m，0）两点，与y 轴相交于点C（0，﹣3），抛物线的顶点为D．（1）求抛物线的解析式；（2）若点E在x轴上，且∠ECB＝∠CBD，求点E的坐标．（3）若P是直线BC下方抛物线上任意一点，过点P作PH⊥x轴于点H，与BC交于点M．①求线段PM长度的最大值．②在①的条件下，若F为y轴上一动点，求PH+HF的最小值．18．（2020•白云区模拟）如图，抛物线y＝x2+bx+c交x轴于点A，B两点，OA＝1，与y轴交于点C，连接AC，tan∠OAC＝3，抛物线的对称轴与x轴交于点D．（1）求点A，C的坐标；（2）若点P在抛物线上，且满足∠PAB＝2∠ACO，求直线PA在与y轴交点的坐标；（3）点Q在抛物线上，且在x轴下方，直线AQ，BQ分别交抛物线的对称轴于点M、N．求证：DM+DN 为定值，并求出这个定值．19．（2020•福安市校级模拟）已知，抛物线y＝ax2，其中a＞0．（1）如图1，若点A、B是此抛物线上两点，且分属于y轴两侧，连接AB与y轴相交于点C，且∠AOB ＝90°．求证：CO=1；（2）如图2，若点A是此抛物线上一点，过点A的直线恰好与此抛物线仅有一个交点，且与y轴交于点B，与x轴相交于点C．求证：AC＝BC．20．（2020•德城区一模）已知，在以O为原点的直角坐标系中，抛物线的顶点为A（﹣1，﹣4），且经过点B（﹣2，﹣3），与x轴分别交于C、D两点．（1）求直线OB以及该抛物线相应的函数表达式；（2）如图1，点M是抛物线上的一个动点，且在直线OB的下方，过点M作x轴的平行线与直线OB 交于点N，求MN的最大值；（3）如图2，过点A的直线交x轴于点E，且AE∥y轴，点P是抛物线上A、D之间的一个动点，直线PC、PD与AE分别交于F、G两点．当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．【题组六】21．（2020•青山区模拟）如图，在平面直角坐标系xOy中，一次函数y=54x+m（m为常数）的图象与x轴交于点A（﹣3，0），与y轴交于点C，以直线x＝1为对称轴的抛物线y＝ax2+bx+c（a、b、c为常数，且a≠0）经过A、C两点，并与x轴的正半轴交于点B（1）求m的值及抛物线的函数表达式；（2）是否存在抛物线上一动点Q，使得△ACQ是以AC为直角边的直角三角形？若存在，求出点Q的横坐标；若存在，请说明理由；（3）若P是抛物线对称轴上一动点，且使△ACP周长最小，过点P任意作一条与y轴不平行的直线交抛物线于M1（x1，y1），M2（x2，y2）两点，试问1δ212是否为定值，如果是，请求出结果，如果不是请说明理由．（参考公式：在平面直角坐标系中，若A（x1，y1），B（x2，y2），则A，B两点间的距离为AB=(1−2)2+(1−2)2）22．（2020•新都区模拟）已知：在平面直角坐标系中，抛物线y＝ax2﹣2ax+4（a＜0）交x轴于点A、B，与y轴交于点C，AB＝6．（1）如图1，求抛物线的解析式；（2）如图2，点R为第一象限的抛物线上一点，分别连接RB、RC，设△RBC的面积为s，点R的横坐标为t，求s与t的函数关系式；（3）在（2）的条件下，如图3，点D在x轴的负半轴上，点F在y轴的正半轴上，点E为OB上一点，点P为第一象限内一点，连接PD、EF，PD交OC于点G，DG＝EF，PD⊥EF，连接PE，∠PEF＝2∠PDE，连接PB、PC，过点R作RT⊥OB于点T，交PC于点S，若点P在BT的垂直平分线上，OB ﹣TS=23，求点R的坐标．23．（2020•自贡）在平面直角坐标系中，抛物线y＝ax2+bx+3与x轴交于点A（﹣3，0）、B（1，0），交y 轴于点N，点M为抛物线的顶点，对称轴与x轴交于点C．（1）求抛物线的解析式；（2）如图1，连接AM，点E是线段AM上方抛物线上一动点，EF⊥AM于点F，过点E作EH⊥x轴于点H，交AM于点D．点P是y轴上一动点，当EF取最大值时：①求PD+PC的最小值；②如图2，Q点为y轴上一动点，请直接写出DQ+14OQ的最小值．24．（2020•凉山州）如图，二次函数y＝ax2+bx+c的图象过O（0，0）、A（1，0）、B（32，32）三点．（1）求二次函数的解析式；（2）若线段OB的垂直平分线与y轴交于点C，与二次函数的图象在x轴上方的部分相交于点D，求直线CD的解析式；（3）在直线CD下方的二次函数的图象上有一动点P，过点P作PQ⊥x轴，交直线CD于Q，当线段PQ的长最大时，求点P的坐标．。

题型二 选择压轴题之几何图形最值问题类型一线段最值问题1. 如图，在△ ABC 中，/ BAC = 90° AB = 3, AC =4,P 为边 BC 上一动点，PE 丄AB 于 E ,PF 丄AC于F , M 为EF 的中点，贝U PM 的最小值为（）和AC 上的动点，贝U PC + PQ 的最小值是（3.如图，在 Rt A ABC 中，/ B = 90° AB = 3, BC = 4，点D 在BC 上，以 AC 为对角线的所有 ？ADCE 中，DE 的最小值是（）点，贝U PC + PD 的最小值为（）A.1.2D. 2.42.如图，在 Rt △ ABC 中，/ ACB = 90°12 A ・5B. 424 C.24D. 5A.3B. 2C.4D. 54.如图，菱形 值是（）ABCD 中，/ ABC = 60° 边长为13, P 是对角线BD 上的一个动点，则2PB + PC 的最小C.3D. 2 + ；35. 如图，在△ ABC 中，AC = BC , / ACB = 90° 点D 在BC 上，BD = 3, DC = 1，点P 是AB 上的动A.4C.1.4AC = 6,若P , Q 分别是AD第3题图第4题图C.6第5题图 第6题图6. 如图，在边长为4的正方形ABCD 中，点E 、F 分别是边BC 、CD 上的动点，且BE = CF ,连接BF 、 DE ，贝U BF + DE 的最小值为（）边BC , CD 上，则△ AMN 周长的最小值为（）1BP ,贝U AP + 2BP 的最小值为A.2 .'5B. 4 ,'57. 如图，在四边形 ABCD 中，/ BAD = 120° / C.2 /3D. 4 ! 3B =Z D = 90° AB = 2, AD = 4，点 M ，点 N 分别在A.3 ：7D. 118.如图，在直角坐标系中，点 （1，5）和（4，0），点C 是y 轴上的一个动点，且 B 、C 三点不在同一条直线上，当△ABC 的周长最小时，点 C 的坐标是（）A.(0，1)B. (0， 2)C.(0， 3)D. (0，4)9.如图，矩形ABCD 中，AB = 8, BC = 6，点 E , F , G , H 分别在矩形 ABCD 各边上，且 AE = CG ,BF = DH ，则四边形 A.4 .'3EFGH 周长的最小值为（）C.8 .' 7B. 10li10.如图，在 Rt △ ABC中，/ ACB = 90° CB = 4, CA = 6, O C 半径为2, P 为圆上一动点，连接 AP ,A. 37B. 6C.2 . 17D. 411.如图，在 Rt △ ABC中, / ACB = 90° AC = 8, BC = 6，动点F 在边BC 上运动，连接 AF ，过点C作CD 丄AF 于点D ，交AB 于点E ，则B 、D 两点之间距离的最小值为 （）A.2B. 4C.2 . 13-3D. 2 . 13-4A 、B 的坐标分别为 \II I ）第9题图第11题图 第12题图12.如图，在等边△ ABC 中，BF 是AC 边上中线, 点D 在BF 上，连接AD ，在AD 的右侧作等边△ ADE ,接AE 、BF ，交于点 G ,连接DG ,则DG 的最小值为（）16.在Rt A ABC 中，/ ACB = 90° AC = 8, BC = 6,点D 是以点 A 为圆心，4为半径的圆上一点，连 接BD ，点M 为BD 中点，线段CM 长度的最大值为（）类型二面积最值问题（拓展）1.如图，点E 为边长为4的等边△ ABC 的BC 边上一动点（点E 不与B 、C 重合），以AE 为边作等边△ AEF ，则△ AEF 面积的最小值是（）2. （2017合肥蜀山区模拟）如图，O O 的半径是2,直线 两个动点，且在直线I 的异侧，若/ AMB = 45°,则四边形 MANB 面积的最大值是（）3. 如图，在矩形 ABCD 中，AD >AB ,点E 、F 分别是BC 、DC 上的点，且 CE + CF = 8，若sin / ABD连接EF ，当△ AEF 周长最小时，/ CFE 的大小是A.30B. 45C.60D. 9013.在平面直角坐标系中，点O 为坐标原点, 占 八A 、B 、C 的坐标分别为 A （ .3, 0）、B （3.'3, 0）、C （0,5），点D 在第一象限内，且/ ADB = 60 °则线段 CD 的长的最小值是（ ）C.2 .'7 — 2D. 2 . 10 — 214.如图, 在 Rt A ABC 中，/ C = 90° AC = 6, BC = 8,点 F 在边 AC 上，并且 CF = 2, 点E 为边BC上的动点，将△ CEF 沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是（A.33C.315.如图, 第14题图第15题图正方形 ABCD 的边长为2,点E 、F 分别是边BC 、CD 的延长线上的动点，且CE =DF ，连A. .;3 — 1B. ,'5 — 1C. ；'3A.8B. 7C.6D. 5A.2l 与O O 相交于A 、B 两点，M 、N 是O O 上的A.2B. 4C.2 .2D. 4 2第1题图C. 34=4，BD = 20,则厶AEF 的面积的最小值为（ ）5+ Z CBP = 90°连接DP ,。

2017年中考数学填空压轴题填空题1（2017浙江衢州第15题)如图,在直角坐标系中，⊙A 的圆心A 的坐标为(-1，0）,半径为1,点P 为直线343+-=x y 上的动点，过点P 作⊙A 的切线,切点为Q ，则切线长PQ 的最小值是__________【答案】22． 【解析】试题解析：连接AP ，PQ ，当AP 最小时，PQ 最小，∴当AP ⊥直线y=﹣34x+3时,PQ 最小, ∵A 的坐标为（﹣1，0），y=﹣34x+3可化为3x+4y ﹣12=0， ∴22|3(1)4012|34+=3， ∴223-1=22．考点：1.切线的性质;2.一次函数的性质.2.（2017重庆A卷第18题）如图，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G,将△EFG沿EF翻折，得到△EFM，连接DM,交EF于点N,若点F是AB的中点，则△EMN的周长是．学科网【答案】【解析】试题解析：如图1，过E作PQ⊥DC，交DC于P,交AB于Q,连接BE，∵DC∥AB，∴PQ⊥AB,∵四边形ABCD是正方形，∴∠ACD=45°，∴△PEC是等腰直角三角形，∴PE=PC，设PC=x,则PE=x，PD=4﹣x，EQ=4﹣x,∴PD=EQ，∵∠DPE=∠EQF=90°，∠PED=∠EFQ，∴△DPE≌△EQF，∴DE=EF,易证明△DEC≌△BEC,∴DE=BE，∴EF=BE，∵EQ ⊥FB ，∴FQ=BQ=12BF, ∵AB=4，F 是AB 的中点,∴BF=2，∴FQ=BQ=PE=1，∴CE=2，Rt △DAF 中，DF=2242=25+，∵DE=EF,DE ⊥EF, ∴△DEF 是等腰直角三角形,∴DE=EF=25=102，∴PD=22DE PE -=3，如图2，∵DC ∥AB ，∴△DGC ∽△FGA ，∴422CG DC DG AG AF FG ====, ∴CG=2AG ，DG=2FG,∴FG=1252533⨯=， ∵22442+=∴CG=233⨯=，∴-=，连接GM、GN,交EF于H，∵∠GFE=45°，∴△GHF是等腰直角三角形,∴3 =，∴EH=EF﹣-=∴∠NDE=∠AEF,∴tan∠NDE=tan∠AEF=EN GH DE EH=,123EN==，∴EN=2，∴NH=EH﹣EN=326-=,Rt△GNH中，6==,由折叠得：MN=GN，EM=EG，∴△EMN的周长=EN+MN+EM=2632+++=考点：1。

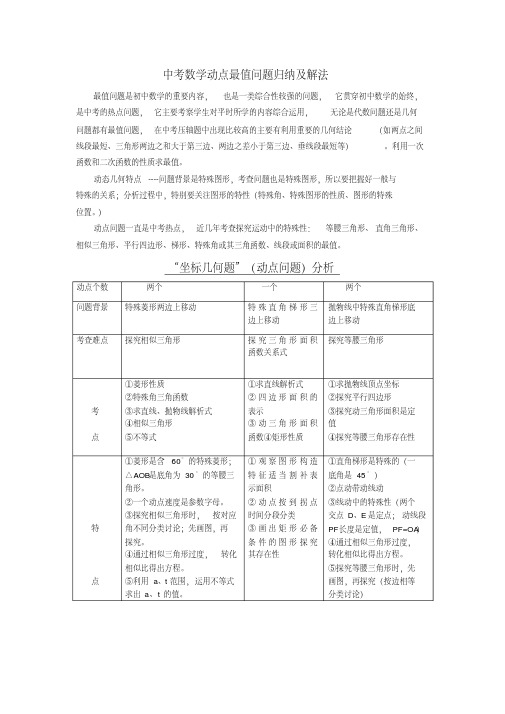
中考数学动点最值问题归纳及解法最值问题是初中数学的重要内容，也是一类综合性较强的问题，它贯穿初中数学的始终，是中考的热点问题，它主要考察学生对平时所学的内容综合运用，无论是代数问题还是几何问题都有最值问题，在中考压轴题中出现比较高的主要有利用重要的几何结论（如两点之间线段最短、三角形两边之和大于第三边、两边之差小于第三边、垂线段最短等）。

利用一次函数和二次函数的性质求最值。

动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

“坐标几何题”（动点问题）分析动点个数两个一个两个问题背景特殊菱形两边上移动特殊直角梯形三边上移动抛物线中特殊直角梯形底边上移动考查难点探究相似三角形探究三角形面积函数关系式探究等腰三角形考点①菱形性质②特殊角三角函数③求直线、抛物线解析式④相似三角形⑤不等式①求直线解析式②四边形面积的表示③动三角形面积函数④矩形性质①求抛物线顶点坐标②探究平行四边形③探究动三角形面积是定值④探究等腰三角形存在性特点①菱形是含60°的特殊菱形；△AOB是底角为30°的等腰三角形。

②一个动点速度是参数字母。

③探究相似三角形时，按对应角不同分类讨论；先画图，再探究。

④通过相似三角形过度，转化相似比得出方程。

⑤利用a、t范围，运用不等式求出a、t的值。

①观察图形构造特征适当割补表示面积②动点按到拐点时间分段分类③画出矩形必备条件的图形探究其存在性①直角梯形是特殊的（一底角是45°）②点动带动线动③线动中的特殊性（两个交点D、E是定点；动线段PF长度是定值，PF=OA）④通过相似三角形过度，转化相似比得出方程。

⑤探究等腰三角形时，先画图，再探究（按边相等分类讨论）近几年共同点：①特殊四边形为背景；②点动带线动得出动三角形；③探究动三角形问题（相似、等腰三角形、面积函数关系式）；④求直线、抛物线解析式；⑤探究存在性问题时，先画出图形，再根据图形性质探究答案。

中考数学压轴题动点产生的定值与最值问题8个专题讲解目录第 1 讲角为定值的常规解法第 2 讲角为定值的高级解法第3讲边为定值的动点问题第4讲线段的和或差为定值的动点问题第5讲比值为定值的动点问题第6讲乘积为定值的动点问题第7讲面积为定值的动点问题第8讲动点产生的几何最值问题第1讲角为定值的常规解法【几何法证明角为定值】（1）三角形内角和定理（2）三角形外角定理（3）等腰三角形底角相等（4）直角三角形两锐角互余（5）平行线的同位角相等、内错角相等、同旁内角互补（6）平行四边形的对角相等、邻角互补（7）等腰梯形底角相等（8）圆所涉及的角的关系：圆心角、圆周角、弦切角定理等【例】如图,平面内两条互相垂直的直线相交于点O,∠MON=90°，点A、B分别在射线O M、ON 上移动，AC是△BAO的角平分线，BD为∠ABN的角平分线，AC与B D的反向延长线交于点P.试问：随着点A、B位置的变化，∠APB的大小是否会变化?若保持不变，请求出∠APB 的度数；若发生变化，求出变化范围。

、【例】如图所示,O的直径A B=4,点P是A B延长线上的一点,过P点作O的切线,切点为C，连接AC.(1)若∠CPA=30°，求P C的长；(2)若点P在A B的延长线上运动，∠CPA的平分线交A C于点M，你认为∠CMP 的大小是否发生变化?若变化，请说明理由；若不变化，求出∠CMP 的大小。

【代数法求角为定值】一般在直角坐标系中，可以用坐标的方法表示出边或角，从而求解具体角为定值的问题。

【例】如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以毎秒1个单位长的速度运动t 秒(t>0),抛物线y = ax2 + bx + c 经过点O和点P,已知矩形A BCD的三个顶点为A(1,0),B(1,−5),D(4,0).(1)求c,b (用含t的代数式表示):(2)当4<t<5时，设抛物线分别与线段A B，CD交于点M，N.①在点P的运动过程中，你认为∠AMP的大小是否会变化?若变化，说明理由；若不变，求出∠AMP 的值；②求△MPN的面积S与t的函数关系式,并求t为何值时,S=218；(3)在矩形A BCD的内部(不含边界)，把横、纵坐标都是整数的点称为“好点”。

【压轴卷】中考数学试题(带答案)(1)一、选择题1．如图所示，已知A （12，y 1），B(2,y 2)为反比例函数1y x =图像上的两点，动点P(x ，0)在x 正半轴上运动，当线段AP 与线段BP 之差达到最大时，点P 的坐标是（ ）A ．(12，0) B ．(1,0) C ．(32,0) D ．(52,0) 2．在数轴上，与表示6的点距离最近的整数点所表示的数是( ) A ．1B ．2C ．3D ．43．阅读理解：已知两点1122,,()(),M x y N x y ，则线段MN 的中点(),K x y 的坐标公式为：122x x x +=，122y y y +=．如图，已知点O 为坐标原点，点()30A -,，O e 经过点A ，点B 为弦PA 的中点．若点(),P a b ，则有,a b 满足等式：229a b +=．设(),B m n ，则,m n 满足的等式是（ ）A ．229m n +=B ．223922m n -⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭C ．()()222323m n ++=D ．()222349m n ++=4．老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：接力中，自己负责的一步出现错误的是（ ）A ．只有乙B ．甲和丁C ．乙和丙D ．乙和丁5．如图，矩形纸片ABCD 中，4AB =，6BC =，将ABC V 沿AC 折叠，使点B 落在点E 处，CE 交AD 于点F ，则DF 的长等于（ ）A ．35B ．53C ．73D ．546．今年我市工业试验区投资50760万元开发了多个项目，今后还将投资106960万元开发多个新项目，每个新项目平均投资比今年每个项目平均投资多500万元，并且新增项目数量比今年多20个．假设今年每个项目平均投资是x 万元，那么下列方程符合题意的是（ ） A ．1069605076020500x x -=+B ．5076010696020500x x -=+ C ．1069605076050020x x-=+D ．5076010696050020x x -=+ 7．某服装加工厂加工校服960套的订单，原计划每天做48套．正好按时完成．后因学校要求提前5天交货，为按时完成订单，设每天就多做x 套，则x 应满足的方程为（ ） A ．96096054848x -=+ B ．96096054848x +=+ C ．960960548x-= D ．96096054848x-=+ 8．“绿水青山就是金山银山”．某工程队承接了60万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了25%，结果提前30天完成了这一任务．设实际工作时每天绿化的面积为x 万平方米，则下面所列方程中正确的是（ ） A ．606030(125%)x x-=+ B ．606030(125%)x x-=+C ．60(125%)6030x x ⨯+-=D ．6060(125%)30x x⨯+-= 9．如图中的几何体是由一个圆柱和个长方体组成的，该几何体的俯视图是( )A ．B ．C ．D ．10．如图，P 为平行四边形ABCD 的边AD 上的一点，E ，F 分别为PB ，PC 的中点，△PEF ，△PDC ，△PAB 的面积分别为S ，1S ，2S ．若S=3，则12S S +的值为（ ）A ．24B ．12C ．6D ．311．均匀的向一个容器内注水，在注水过程中，水面高度h 与时间t 的函数关系如图所示，则该容器是下列中的（ ）A ．B ．C ．D ．12．下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（ ） A ．B ．C ．D ．二、填空题13．如图，△ABC 的三个顶点均在正方形网格格点上，则tan ∠BAC =_____________．14．中国的陆地面积约为9 600 000km 2，把9 600 000用科学记数法表示为 ． 15．当直线()223y k x k =-+-经过第二、三、四象限时，则k 的取值范围是_____． 16．3x +x 的取值范围是_____．17．“复兴号”是我国具有完全自主知识产权、达到世界先进水平的动车组列车．“复兴号”的速度比原来列车的速度每小时快40千米，提速后从北京到上海运行时间缩短了30分钟，已知从北京到上海全程约1320千米，求“复兴号”的速度．设“复兴号”的速度为x 千米/时，依题意，可列方程为_____． 18．分解因式：2x 2﹣18＝_____．19．从﹣2，﹣1，1，2四个数中，随机抽取两个数相乘，积为大于﹣4小于2的概率是_____．20．在学校组织的义务植树活动中，甲、乙两组各四名同学的植树棵数如下，甲组：9，9，11，10；乙组：9，8，9，10；分别从甲、乙两组中随机选取一名同学，则这两名同学的植树总棵数为19的概率______．三、解答题21．某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示，成本y2与销售月份x之间的关系如图2所示（图1的图象是线段，图2的图象是抛物线）（1）已知6月份这种蔬菜的成本最低，此时出售每千克的收益是多少元？（收益=售价﹣成本）（2）哪个月出售这种蔬菜，每千克的收益最大？简单说明理由．（3）已知市场部销售该种蔬菜4、5两个月的总收益为22万元，且5月份的销售量比4月份的销售量多2万千克，求4、5两个月的销售量分别是多少万千克？22．某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：（1）这次调查的学生共有多少名；（2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数；（3）如果要在这个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．23．已知关于x的方程220++-=.x ax a（1）当该方程的一个根为1时，求a的值及该方程的另一根；（2）求证：不论a取何实数，该方程都有两个不相等的实数根.24．修建隧道可以方便出行.如图：A ，B 两地被大山阻隔，由A 地到B 地需要爬坡到山顶C 地，再下坡到B 地.若打通穿山隧道，建成直达A ，B 两地的公路，可以缩短从A 地到B 地的路程.已知：从A 到C 坡面的坡度1:3i =，从B 到C 坡面的坡角45CBA ∠=︒，42BC =公里.（1）求隧道打通后从A 到B 的总路程是多少公里？（结果保留根号）（2）求隧道打通后与打通前相比，从A 地到B 地的路程约缩短多少公里？（结果精确到0.012 1.414≈3 1.732） 25．解方程：3x x +﹣1x=1．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【解析】 【分析】求出AB 的坐标，设直线AB 的解析式是y=kx+b ，把A 、B 的坐标代入求出直线AB 的解析式，根据三角形的三边关系定理得出在△ABP 中，|AP-BP|＜AB ，延长AB 交x 轴于P′，当P 在P′点时，PA-PB=AB ，此时线段AP 与线段BP 之差达到最大，求出直线AB 于x 轴的交点坐标即可． 【详解】 ∵把A （12，y 1），B （2，y 2）代入反比例函数y=1x 得：y 1=2，y 2=12， ∴A （12，2），B （2，12）， ∵在△ABP 中，由三角形的三边关系定理得：|AP-BP|＜AB ， ∴延长AB 交x 轴于P′，当P 在P′点时，PA-PB=AB ， 即此时线段AP 与线段BP 之差达到最大，设直线AB 的解析式是y=kx+b ， 把A 、B 的坐标代入得：122122k b k b ⎧+⎪⎪⎨⎪+⎪⎩＝＝， 解得：k=-1，b=52， ∴直线AB 的解析式是y=-x+52， 当y=0时，x=52， 即P （52，0）， 故选D ． 【点睛】本题考查了三角形的三边关系定理和用待定系数法求一次函数的解析式的应用，解此题的关键是确定P 点的位置，题目比较好，但有一定的难度．2．B解析：B 【解析】 【分析】6的大小，即可得到结果． 【详解】46 6.25<<Q ，26 2.5∴<<，6的点距离最近的整数点所表示的数是2， 故选：B ． 【点睛】此题考查了实数与数轴，以及算术平方根，熟练掌握各自的性质是解本题的关键．3．D解析：D 【解析】 【分析】根据中点坐标公式求得点B 的坐标，然后代入,a b 满足的等式进行求解即可. 【详解】∵点()30A -,，点(),P a b ，点(),B m n 为弦PA 的中点， ∴32a m -+=，02b n +=， ∴23,2a m b n =+=，又,a b 满足等式：229a b +=， ∴()222349m n ++=， 故选D ． 【点睛】本题考查了坐标与图形性质，解题的关键是理解中点坐标公式．4．D解析：D 【解析】【分析】根据分式的乘除运算步骤和运算法则逐一计算即可判断．【详解】∵22211x x x x x-÷--=2221·1x x x x x --- =()2212·1x x x x x---- =()()221·1x x x x x ---- =()2x x --=2x x-， ∴出现错误是在乙和丁，故选D ．【点睛】本题考查了分式的乘除法，熟练掌握分式乘除法的运算法则是解题的关键.5．B解析：B 【解析】 【分析】由折叠的性质得到AE=AB ，∠E=∠B=90°，易证Rt △AEF ≌Rt △CDF ，即可得到结论EF=DF ；易得FC=FA ，设FA=x ，则FC=x ，FD=6-x ，在Rt △CDF 中利用勾股定理得到关于x 的方程x 2=42+（6-x ）2，解方程求出x 即可．【详解】∵矩形ABCD 沿对角线AC 对折，使△ABC 落在△ACE 的位置， ∴AE=AB ，∠E=∠B=90°， 又∵四边形ABCD 为矩形， ∴AB=CD ， ∴AE=DC ， 而∠AFE=∠DFC ， ∵在△AEF 与△CDF 中，AFE CFD E DAE CD ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△AEF ≌△CDF （AAS ）， ∴EF=DF ；∵四边形ABCD 为矩形， ∴AD=BC=6，CD=AB=4， ∵Rt △AEF ≌Rt △CDF ， ∴FC=FA ，设FA=x ，则FC=x ，FD=6-x ，在Rt △CDF 中，CF 2=CD 2+DF 2，即x 2=42+（6-x ）2，解得x ＝133， 则FD ＝6-x=53. 故选B ． 【点睛】考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应边相等．也考查了矩形的性质和三角形全等的判定与性质以及勾股定理．6．A解析：A 【解析】试题分析：∵今后项目的数量﹣今年的数量=20，∴1069605076020500x x-=+．故选A ．考点：由实际问题抽象出分式方程．7．D解析：D 【解析】解：原来所用的时间为：96048，实际所用的时间为：96048x +，所列方程为：96096054848x -=+．故选D ．点睛：本题考查了由实际问题抽象出分式方程，关键是时间作为等量关系，根据每天多做x 套，结果提前5天加工完成，可列出方程求解．8．C解析：C 【解析】分析：设实际工作时每天绿化的面积为x 万平方米，根据工作时间=工作总量÷工作效率结合提前 30 天完成任务，即可得出关于x 的分式方程．详解：设实际工作时每天绿化的面积为x 万平方米，则原来每天绿化的面积为125%x+万平方米，依题意得：606030125%x x-=+，即()60125%6030x x⨯+-=． 故选C ．点睛：考查了由实际问题抽象出分式方程．找到关键描述语，找到合适的等量关系是解决问题的关键．9．D解析：D 【解析】 【分析】根据从上边看得到的图形是俯视图，可得答案． 【详解】解：从上边看是一个圆形，圆形内部是一个虚线的正方形. 故选：D ． 【点睛】本题考查了简单组合体的三视图，从上边看得到的图形是俯视图．10．B解析：B 【解析】 【分析】 【详解】过P 作PQ ∥DC 交BC 于点Q ，由DC ∥AB ，得到PQ ∥AB ， ∴四边形PQCD 与四边形APQB 都为平行四边形， ∴△PDC ≌△CQP ，△ABP ≌△QPB ， ∴S △PDC =S △CQP ，S △ABP =S △QPB ， ∵EF 为△PCB 的中位线， ∴EF ∥BC ，EF=12BC ， ∴△PEF ∽△PBC ，且相似比为1：2，∴S△PEF：S△PBC=1：4，S△PEF=3，S S =12．∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=12故选B．11．D解析：D【解析】【分析】由函数图象可得容器形状不是均匀物体分析判断，由图象及容积可求解．【详解】根据图象折线可知是正比例函数和一次函数的函数关系的大致图象；切斜程度（即斜率）可以反映水面升高的速度；因为D几何体下面的圆柱体的底圆面积比上面圆柱体的底圆面积小,所以在均匀注水的前提下是先快后慢;故选D.【点睛】此题主要考查了函数图象，解决本题的关键是根据用的时间长短来判断相应的函数图象．12．B解析：B【解析】分析：根据轴对称图形与中心对称图形的概念求解即可．详解：A．是轴对称图形，不是中心对称图形；B．是轴对称图形，也是中心对称图形；C．是轴对称图形，不是中心对称图形；D．是轴对称图形，不是中心对称图形．故选B．点睛：本题考查了中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．二、填空题13．【解析】分析：在图形左侧添加正方形网格分别延长ABAC连接它们延长线所经过的格点可构成直角三角形利用正切的定义即可得出答案详解：如图所示由图形可知∴tan∠BAC=故答案为点睛：本题考查了锐角三角函解析：13【解析】分析：在图形左侧添加正方形网格，分别延长AB 、AC ，连接它们延长线所经过的格点，可构成直角三角形，利用正切的定义即可得出答案. 详解：如图所示，由图形可知，90AFE ∠=︒，3AF AC =，EF AC =， ∴tan ∠BAC =133EF AC AF AC ==. 故答案为13. 点睛：本题考查了锐角三角函数的定义. 利用网格构建直角三角形进而利用正切的定义进行求解是解题的关键.14．6×106【解析】【分析】【详解】将9600000用科学记数法表示为96×106故答案为96×106解析：6×106． 【解析】 【分析】 【详解】将9600000用科学记数法表示为9.6×106． 故答案为9.6×106． 15．【解析】【分析】根据一次函数时图象经过第二三四象限可得即可求解；【详解】经过第二三四象限∴∴∴故答案为：【点睛】本题考查一次函数图象与系数的关系；掌握一次函数与对函数图象的影响是解题的关键解析：13k <<. 【解析】 【分析】根据一次函数y kx b =+，k 0<，0b <时图象经过第二、三、四象限，可得220k -<，30k -<，即可求解；【详解】()223y k x k =-+-经过第二、三、四象限，∴220k -<，30k -<，∴1k >，3k <， ∴13k <<， 故答案为：13k <<. 【点睛】本题考查一次函数图象与系数的关系；掌握一次函数y kx b =+，k 与b 对函数图象的影响是解题的关键．16．x≥﹣3【解析】【分析】直接利用二次根式的定义求出x 的取值范围【详解】解：若式子在实数范围内有意义则x+3≥0解得：x≥﹣3则x 的取值范围是：x≥﹣3故答案为：x≥﹣3【点睛】此题主要考查了二次根式解析：x ≥﹣3【解析】 【分析】直接利用二次根式的定义求出x 的取值范围． 【详解】.在实数范围内有意义， 则x +3≥0， 解得：x ≥﹣3，则x 的取值范围是：x ≥﹣3． 故答案为：x ≥﹣3． 【点睛】此题主要考查了二次根式有意义的条件，正确把握二次根式的定义是解题关键．17．【解析】【分析】设复兴号的速度为x 千米/时则原来列车的速度为（x-40）千米/时根据提速后从北京到上海运行时间缩短了30分钟列出方程即可【详解】设复兴号的速度为x 千米/时则原来列车的速度为（x ﹣40解析：13201320304060x x -=-． 【解析】 【分析】设“复兴号”的速度为x 千米/时，则原来列车的速度为（x-40）千米/时，根据提速后从北京到上海运行时间缩短了30分钟列出方程即可． 【详解】设“复兴号”的速度为x 千米/时，则原来列车的速度为（x ﹣40）千米/时， 根据题意得：13201320304060x x -=-． 故答案为：13201320304060x x -=-． 【点睛】本题主要考查由实际问题抽象出分式方程，解题的关键是理解题意，找到题目蕴含的相等关系．18．2（x+3）（x﹣3）【解析】【分析】原式提取2再利用平方差公式分解即可【详解】原式＝2（x2﹣9）＝2（x+3）（x﹣3）故答案为：2（x+3）（x﹣3）【点睛】此题考查了提公因式法与公式法的综合解析：2（x+3）（x﹣3）【解析】【分析】原式提取2，再利用平方差公式分解即可．【详解】原式＝2（x2﹣9）＝2（x+3）（x﹣3），故答案为：2（x+3）（x﹣3）【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．19．【解析】【分析】列表得出所有等可能结果从中找到积为大于-4小于2的结果数根据概率公式计算可得【详解】列表如下： -2 -1 1 2 -2 2 -2 -4 -1 2 -1 -2 1 -2 -解析：1 2【解析】【分析】列表得出所有等可能结果，从中找到积为大于-4小于2的结果数，根据概率公式计算可得．【详解】列表如下：∴积为大于-4小于2的概率为612=12，故答案为12．【点睛】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．20．【解析】【分析】【详解】画树状图如图：∵共有16种等可能结果两名同学的植树总棵数为19的结果有5种结果∴这两名同学的植树总棵数为19的概率为解析：5 16．【解析】【分析】【详解】画树状图如图：∵共有16种等可能结果，两名同学的植树总棵数为19的结果有5种结果，∴这两名同学的植树总棵数为19的概率为5 16.三、解答题21．（1）6月份出售这种蔬菜每千克的收益是2元．（2）5月份出售这种蔬菜，每千克的收益最大．（3）4月份的销售量为4万千克，5月份的销售量为6万千克．【解析】分析：（1）找出当x=6时，y1、y2的值，二者作差即可得出结论；（2）观察图象找出点的坐标，利用待定系数法即可求出y1、y2关于x的函数关系式，二者作差后利用二次函数的性质即可解决最值问题；（3）求出当x=4时，y1﹣y2的值，设4月份的销售量为t万千克，则5月份的销售量为（t+2）万千克，根据总利润=每千克利润×销售数量，即可得出关于t的一元一次方程，解之即可得出结论．详解：（1）当x=6时，y1=3，y2=1，∵y1﹣y2=3﹣1=2，∴6月份出售这种蔬菜每千克的收益是2元．（2）设y1=mx+n，y2=a（x﹣6）2+1．将（3，5）、（6，3）代入y1=mx+n，3563m n m n +=⎧⎨+=⎩，解得：237m n ⎧=-⎪⎨⎪=⎩， ∴y 1=﹣23x+7； 将（3，4）代入y 2=a （x ﹣6）2+1， 4=a （3﹣6）2+1，解得：a=13， ∴y 2=13（x ﹣6）2+1=13x 2﹣4x+13． ∴y 1﹣y 2=﹣23x+7﹣（13x 2﹣4x+13）=﹣13x 2+103x ﹣6=﹣13（x ﹣5）2+73． ∵﹣13＜0， ∴当x=5时，y 1﹣y 2取最大值，最大值为73， 即5月份出售这种蔬菜，每千克的收益最大．（3）当t=4时，y 1﹣y 2=﹣13x 2+103x ﹣6=2．设4月份的销售量为t 万千克，则5月份的销售量为（t+2）万千克， 根据题意得：2t+73（t+2）=22， 解得：t=4， ∴t+2=6．答：4月份的销售量为4万千克，5月份的销售量为6万千克．点睛：本题考查了待定系数法求一次（二次）函数解析式、二次函数的性质以及一元一次方程的应用，解题的关键是：（1）观察函数图象，找出当x=6时y 1﹣y 2的值；（2）根据点的坐标，利用待定系数法求出y 1、y 2关于x 的函数关系式；（3）找准等量关系，正确列出一元一次方程．22．（1）280名；（2）补图见解析；108°；（3）0.1. 【解析】 【分析】（1）根据“平等”的人数除以占的百分比得到调查的学生总数即可；（2）求出“互助”与“进取”的学生数，补全条形统计图，求出“进取”占的圆心角度数即可；（3）列表或画树状图得出所有等可能的情况数，找出恰好选到“C”与“E”的情况数，即可求出所求的概率． 【详解】解：（1）56÷20%=280（名），答：这次调查的学生共有280名；（2）280×15%=42（名），280﹣42﹣56﹣28﹣70=84（名），补全条形统计图，如图所示，根据题意得：84÷280=30%，360°×30%=108°，答：“进取”所对应的圆心角是108°；（3）由（2）中调查结果知：学生关注最多的两个主题为“进取”和“感恩”用列表法为：A B C D EA（A，B）（A，C）（A，D）（A，E）B（B，A）（B，C）（B，D）（B，E）C（C，A）（C，B）（C，D）（C，E）D（D，A）（D，B）（D，C）（D，E）E（E，A）（E，B）（E，C）（E，D）共20种情况，恰好选到“C”和“E”有2种，∴恰好选到“进取”和“感恩”两个主题的概率是0.1．23．（1）12，32；（2）证明见解析.【解析】试题分析：（1）根据一元二次方程根与系数的关系列方程组求解即可.（2）要证方程都有两个不相等的实数根，只要证明根的判别式大于0即可.试题解析：（1）设方程的另一根为x1，∵该方程的一个根为1，∴1111{211a x a x +=--⋅=.解得132{12x a =-=. ∴a 的值为12，该方程的另一根为32-.（2）∵()()222241248444240a a a a a a a ∆=-⋅⋅-=-+=-++=-+>， ∴不论a 取何实数，该方程都有两个不相等的实数根.考点：1.一元二次方程根与系数的关系；2. 一元二次方程根根的判别式；3.配方法的应用. 24．（1）隧道打通后从A 到B 的总路程是(434)+公里;（2）隧道打通后与打通前相比，从A 地到B 地的路程约缩短2.73公里. 【解析】 【分析】（1）过点C 作CD ⊥AB 于点D ，利用锐角三角函数的定义求出CD 及AD 的长，进而可得出结论．（2）由坡度可以得出A ∠的度数，从而得出AC 的长，根据AC CB AB +-即可得出缩短的距离. 【详解】（1）作CD AB ⊥于点D ，在Rt BCD ∆中，∵45CBA ∠=︒，42BC =， ∴4CD BD ==. 在Rt ACD ∆中， ∵1:3CDi AD==， ∴343AD CD ==， ∴()434AB =+公里.答：隧道打通后从A 到B 的总路程是()434+公里.（2）在Rt ACD ∆中， ∵3CDi AD==， ∴30A ∠=︒，∴2248AC CD ==⨯=，∴8AC CB +=+∵4AB =，∴84 2.73AC CB AB +-=+≈（公里）.答：隧道打通后与打通前相比，从A 地到B 地的路程约缩短2.73公里. 【点睛】本题考查的是解直角三角形的应用-坡度问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，需要熟记坡度和锐角三角函数的定义． 25．分式方程的解为x=﹣34． 【解析】【分析】方程两边都乘以x （x+3）得出方程x ﹣1+2x=2，求出方程的解，再代入x （x+3）进行检验即可．【详解】两边都乘以x （x+3），得：x 2﹣（x+3）=x （x+3）， 解得：x=﹣34， 检验：当x=﹣34时，x （x+3）=﹣2716≠0， 所以分式方程的解为x=﹣34． 【点睛】本题考查了解分式方程，熟练掌握解分式方程的方法与注意事项是解题的关键.。

利用二次函数的对称性求最小值1．如图,抛物线217322y x x =++与直线1122y x =--交于,A B 两点,点C 为y 轴上点,当ABC 周长最短时;周长的值为（ ）A 7353B 7335C 4335D 4353【答案】B【解析】【分析】 联立方程先求出抛物线和直线的交点坐标，然后已知在ABC 中的边AB 的长已经确定，只需要求出AC BC +的最小值即可，可以做B 点关于y 轴的对称点B ',连接AB '交y 轴于点C ，此时AB '就为AC BC +的最小值，所以ABC 周长最短为+AB AB '的长，求出即可.【详解】解：根据题意联立方程得：2173221122y x x y x ⎧=++⎪⎪⎨⎪=--⎪⎩，得出71x x =-=-、，把横坐标分别代入表达式得出交点坐标， 即：(7,3)A -,(1,0)B -,已知在ABC 中的边AB 的长已经确定，做B 点关于y 轴的对称点B ',连接AB '交y 轴于点C,如图所示， 此时AB '就为AC BC +的最小值,2296473AB AD DB ''=+=+=2293635AB AD DB =+=+=ABC ∴周长最小为：7335+;故选B.【点睛】本题考查的是两个函数图像的交点问题，以及求线段的最小值问题，需要根据题意去解读信息，借助于勾股定理去求最终结果.2．已知抛物线2114y x =+具有如下性质：抛物线上任意一点到定点F （0,2）的距离与到x 轴的距离相等，点M 的坐标为（3,6），P 是抛物线2114y x =+上一动点，则△PMF 周长的最小值是（ ）A ．5B ．9C ．11D ．13【答案】C【解析】【分析】 过点M 作ME ⊥x 轴于点E ，交抛物线2114y x =+于点P ，由PF=PE 结合三角形三边关系，即可得出此时△PMF 周长最小，再由点F 、M 的坐标即可得出MF 、ME 的长度，进而得出△PMF 周长的最小值.【详解】如图过点M 作ME ⊥x 轴于点E ，交抛物线2114y x =+于点P ，此时△PMF 周长最小 ∵F （0,2）M （3,6），∴ME=6，FM 22(30)(62)5=-+-= ∴△PMF 周长的最小值=ME+FM=6+5=11 故选C【点睛】 本题考查了二次函数的性质和最短路径问题，熟练掌握各个知识点是解题关键.，3．如图，抛物线y=x 2+bx-2与x 轴交于A 、B 两点，与y 交于C 点，且A （-1，0），点M （m ，0）是x 轴上的一个动点，当MC+MD 的值最小时，m 的值是（ ）A ．B ．C ．D ．【答案】B【解析】 试题分析：∵点A （-1，0）在抛物线y=x 2+bx-2上，∴×（-1）2+b×（-1）-2=0，∴b=-，∴抛物线的解析式为y=x 2-x-2，∴顶点D 的坐标为（，-），作出点C 关于x 轴的对称点C′，则C′（0，2），OC′=2连接C′D 交x 轴于点M ，根据轴对称性及两点之间线段最短可知，MC+MD 的值最小．设抛物线的对称轴交x 轴于点E ．∵ED ∥y 轴，∴∠OC′M=∠EDM ，∠C′OM=∠DEM∴△C′OM ∽△DEM ． ∴， 即，∴m=．故选B ．考点：1.轴对称-最短路线问题；2.二次函数的性质；3.相似三角形的判定与性质．4．如图，顶点为M 的抛物线23y ax bx =++与x 轴交于()3,0A ，()1,0B -两点，与y 轴交于点C ．（1）请求此抛物线的函数解析式；（2）在抛物线的对称轴上有一点Q ，使得QBC ∆的周长最小，请求出点Q 的坐标； （3）在直线AC 的上方的抛物线上，是否存在一点P （不与点M 重合），使得ACP ∆的面积等于ACM ∆的面积，若存在，请求出点P 的坐标；若不存在，请说明理由．【答案】（1）2y x 2x 3=-++；（2）点Q 的坐标为()1,2；（3）存在，点P 的坐标为：()2,3【解析】【分析】（1）根据抛物线23y ax bx =++与x 轴交于()3,0A ，()1,0B -，可得抛物线的表达式为(1)(3)y a x x =+-，展开即可求解；（2）根据题意得抛物线的对称轴为：1312x -+==，由抛物线的对称性可知，点B 关于对称轴1x =的对称点是点A ，所以BQ=AQ ，要使QCB △的周长最小，只需AQ+CQ 最小即可，连接AC ，交对称轴点Q ，此时AQ+CQ 最小，即QCB △的周长最小，利用待定系数法求出直线AC 的解析式，然后令x=1即可求出C 点坐标；（3）过点M 作直线//m AC ，直线m 与抛物线交点即为点P ，根据点M 的坐标可求出m 直线的表达式，联立抛物线的解析式与直线m 的解析式即可求出点P 的坐标．【详解】解：（1）抛物线23y ax bx =++与x 轴交于()3,0A ，()1,0B -， ∴抛物线的表达式为：(1)(3)y a x x =+-()223a x x =--=223ax ax a --， 故33a -=，解得：1a =-，故抛物线的表达式为：2y x 2x 3=-++ ；（2）由题意可知抛物线的对称轴为： 1312x -+==， 由抛物线的对称性可知，点B 关于对称轴1x =的对称点是点A ，∴BQ=AQ ，∵QCB △的周长=QC+BQ+BC ，∴QCB △的周长=QC+AQ+BC ，要使QCB △的周长最小，只需AQ+CQ 最小，连接AC ，交对称轴点Q ，此时QCB △的周长最小，当0x =时，3y =，()0,3C ∴，设直线AC 的解析式为y kx b =+，把()3,0A ，()0,3C 代入，则303k b b +=⎧⎨=⎩， 解得13k b =-⎧⎨=⎩， ∴直线AC 的解析式为3y x =-+，当1x =时，2y =，∴点Q 的坐标为()1,2；（3）存在．过点M 作直线//m AC ，直线m 与抛物线交点即为点P ，点()1,4M ，则m 直线的表达式为：5y x =-+，∴2235y x x y x ⎧=-++⎨=-+⎩整理得2320x x -+-=解得：1x =（舍去）2x =；故点P 的坐标为：()2,3；【点睛】本题是二次函数的综合运用，考查了求二次函数的解析式和性质，求一次函数解析式，平行线的性质等知识．掌握平行线间的距离相等是解（3）题的关键．5．如图，抛物线经过A （﹣1，0），B （5，0），C （0，52-）三点．（1）求抛物线的解析式；（2）在抛物线的对称轴上有一点P ，使PA+PC 的值最小，求点P 的坐标；（3）点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A ，C ，M ，N 四点构成的四边形为平行四边形？若存在，求点N 的坐标；若不存在，请说明理由．【答案】（1）抛物线的解析式为：215y x 2x 22=--． （2）P （2，52-）． （3）存在点N 的坐标为（4，52-），（214-，52）或（214+，52） 【解析】【分析】 本题考查的是二次函数综合题，涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识，在解答（3）时要注意进行分类讨论．（1）设抛物线的解析式为y=ax 2+bx+c （a≠0），再把A （﹣1，0），B （5，0），C （0，）三点代入求出a 、b 、c 的值即可；（2）因为点A 关于对称轴对称的点B 的坐标为（5，0），连接BC 交对称轴直线于点P ，求出P 点坐标即可；（3）分点N 在x 轴下方或上方两种情况进行讨论．【详解】解：（1）设抛物线的解析式为y=ax 2+bx+c （a≠0），∵A （﹣1，0），B （5，0），C （0，）三点在抛物线上，∴，解得．∴抛物线的解析式为：y=x2﹣2x﹣；（2）∵抛物线的解析式为：y=x2﹣2x﹣，∴其对称轴为直线x=﹣=﹣=2，连接BC，如图1所示，∵B（5，0），C（0，﹣）∴设直线BC的解析式为y=kx+b（k≠0），∴，解得，∴直线BC的解析式为y=x﹣，当x=2时，y=1﹣=﹣∴P（2，﹣）；（3）存在．如图2所示，①当点N在x轴下方时，∵抛物线的对称轴为直线x=2，C（0，﹣）∴N1（4，﹣）；②当点N在x轴上方时，如图2，过点N2作N2D⊥x轴于点D，在△AN2D与△M2CO中，∴△AN2D≌△M2CO（ASA）∴N2D=OC=，即N2点的纵坐标为．∴x2﹣2x﹣=，解得x=2+或x=2﹣，∴N2（2+，），N3（2﹣，）．综上所述，符合条件的点N的坐标为N1（4，﹣），N2（2+，）或N3（2﹣，）．考点：二次函数综合题．6．如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．（1）求抛物线及直线AC的函数关系式；（2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；（3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．【答案】（1）y＝﹣x2﹣2x+3；y＝﹣x+1；（2）当x＝﹣12时，△APC的面积取最大值，最大值为278，此时点P的坐标为（﹣12，154）；（3）在对称轴上存在一点M（﹣1，2），使△ANM的周长最小，△ANM周长的最小值为102【解析】【分析】（1）根据点A ，C 的坐标，利用待定系数法即可求出抛物线及直线AC 的函数关系式；（2）过点P 作PE ∥y 轴交x 轴于点E ，交直线AC 于点F ，过点C 作CQ ∥y 轴交x 轴于点Q ，设点P 的坐标为（x ，﹣x 2﹣2x +3）（﹣2＜x ＜1），则点E 的坐标为（x ，0），点F 的坐标为（x ，﹣x +1），进而可得出PF 的值，由点C 的坐标可得出点Q 的坐标，进而可得出AQ 的值，利用三角形的面积公式可得出S △APC ＝﹣32x 2﹣32x +3，再利用二次函数的性质，即可解决最值问题；（3）利用二次函数图象上点的坐标特征可得出点N 的坐标，利用配方法可找出抛物线的对称轴，由点C ，N 的坐标可得出点C ，N 关于抛物线的对称轴对称，令直线AC 与抛物线的对称轴的交点为点M ，则此时△ANM 周长取最小值，再利用一次函数图象上点的坐标特征求出点M 的坐标，以及利用两点间的距离公式结合三角形的周长公式求出△ANM 周长的最小值即可得出结论．【详解】（1）将A （1，0），C （﹣2，3）代入y ＝﹣x 2+bx +c ，得：10423b c b c -++=⎧⎨--+=⎩，解得：23b c =-⎧⎨=⎩， ∴抛物线的函数关系式为y ＝﹣x 2﹣2x +3；设直线AC 的函数关系式为y ＝mx +n （m ≠0），将A （1，0），C （﹣2，3）代入y ＝mx +n ，得：023m n m n +=⎧⎨-+=⎩，解得：11m n =-⎧⎨=⎩， ∴直线AC 的函数关系式为y ＝﹣x +1．（2）过点P 作PE ∥y 轴交x 轴于点E ，交直线AC 于点F ，过点C 作CQ ∥y 轴交x 轴于点Q ，如图1所示．设点P 的坐标为（x ，﹣x 2﹣2x +3）（﹣2＜x ＜1），则点E 的坐标为（x ，0），点F 的坐标为（x ，﹣x +1），∴PE ＝﹣x 2﹣2x +3，EF ＝﹣x +1，EF ＝PE ﹣EF ＝﹣x 2﹣2x +3﹣（﹣x +1）＝﹣x 2﹣x +2． ∵点C 的坐标为（﹣2，3），∴点Q 的坐标为（﹣2，0），∴AQ ＝1﹣（﹣2）＝3，∴S △APC ＝12AQ •PF ＝﹣32x 2﹣32x +3＝﹣32（x +12）2+278．∵﹣32＜0， ∴当x ＝﹣12时，△APC 的面积取最大值，最大值为278，此时点P 的坐标为（﹣12，154）． （3）当x ＝0时，y ＝﹣x 2﹣2x +3＝3， ∴点N 的坐标为（0，3）． ∵y ＝﹣x 2﹣2x +3＝﹣（x +1）2+4， ∴抛物线的对称轴为直线x ＝﹣1． ∵点C 的坐标为（﹣2，3），∴点C ，N 关于抛物线的对称轴对称．令直线AC 与抛物线的对称轴的交点为点M ，如图2所示． ∵点C ，N 关于抛物线的对称轴对称， ∴MN ＝CM ，∴AM +MN ＝AM +MC ＝AC ， ∴此时△ANM 周长取最小值． 当x ＝﹣1时，y ＝﹣x +1＝2， ∴此时点M 的坐标为（﹣1，2）．∵点A 的坐标为（1，0），点C 的坐标为（﹣2，3），点N 的坐标为（0，3）， ∴AC ＝2233+ ＝32，AN ＝2231+ ＝10， ∴C △ANM ＝AM +MN +AN ＝AC +AN ＝32+10．∴在对称轴上存在一点M （﹣1，2），使△ANM 的周长最小，△ANM 周长的最小值为32+10．【点睛】本题考查待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长，解题的关键是：（1）根据点的坐标，利用待定系数法求出抛物线及直线AC 的函数关系式；（2）利用三角形的面积公式找出S △APC ＝﹣32x 2﹣32x +3的最值；（3）利用二次函数图象的对称性结合两点之间线段最短找出点M 的位置． 7．如图，抛物线y=12x 2+mx+4m 与x 轴交于点A(1x ，0）和点B(2x ，0)，与y 轴交于点C ，22121220x x x x +=且、满足，若对称轴在y 轴的右侧． （1）求抛物线的解析式（2）在抛物线的对称轴上取一点M ，使|MC-MB|的值最大；（3）点Q 是抛物线上任意一点，过点Q 作PQ ⊥x 轴交直线BC 于点P ，连接CQ ，当△CPQ 是等腰三角形时，求点P 的坐标．【答案】（1）y=212x -x-4；（2）M(1，-6)；（3）P 1 (42222--，，P 2(2，-2)，P 3(42222+，． 【解析】 【分析】（1）利用根与系数的关系即可求出m ，结合对称轴在y 轴右侧可得结果；（2）根据点A 和点B 关于对称轴对称，过点AC 作直线交对称轴于点M ，求出A ，B ，C 的坐标，求出AC 的表达式，得到点M 的坐标即可；（3）分PC=PQ ，QC=QP ，CP=CQ 分别讨论，求出相应x 值即可. 【详解】解：（1）∵y=12x 2+mx+4m 与x 轴交于1(x ，0)和点B(2x ，0)， ∴12 x x 、是方程12x 2+mx+4m=0的两个根，122x x m ∴+=-，128x x m ∴=，221220x x +=∴(-2m)2-16m=20， 解得m 1=5，m 2=-1， ∵对称轴在y 轴的右侧， ∴m=-1，∴y=212x -x-4； （2）y=212x -x-4中，当x=0时，y=-4，当y=0时1x =-2，2x =4， ∴A(-2，0)，B(4，0)，C(0，-4)， 过点AC 作直线交对称轴于点M ， 设直线AC 的解析式为y=kx+b ， 将(-2，0)，(0，-4)代入， 则024k bb=-+⎧⎨-=⎩，解得24k b =-⎧⎨=-⎩，得y=-2x-4，当x=1时，y=-6， ∴M(1，-6)；（3）直线BC 的解析式为y=k 1x+b 1， 将(4，0)，(0，-4)代入，则111044k b b =+⎧⎨-=⎩，解得1114k b =⎧⎨=-⎩，得y=x-4，∴∠OCB=∠OBC=45°，设P 的横坐标为x ，作PH ⊥y 轴于H ， 则PC=2x，∴PQ=|(x-4)-212x （-x-4）|（图一） （图二）如图一图二，当CQ=CP 时，(x-4)+212x （-x-4）=-8， x=0，不合题意，所以不存在；（图三） （图四） （图五）如图三，当PC=PQ 2x =(x-4)-212x （-x-4）， 解得x=42- ∴P(42222--，如图四，当CQ=PQ 时，x=(x-4)-212x （-x-4）， 解得x=2， ∴P(2，-2)；如图五，当PC=PQ 时 ，212x （-x-4）2x ， 解得：x=422+， ∴P(42222+，；综上：P 1(42222--，，P 2(2，-2)，P 3(42222+，【点睛】本题是二次函数综合题，考查了待定系数法求二次函数表达式，二次函数的图像和性质，最值问题，等腰三角形的性质，解题的关键是学会分类讨论，利用等腰三角形的性质解题.8．已知y 是x 的二次函数，该函数的图象经过点A(0，5)、B(1，2)、C(3，2)． （1）求该二次函数的表达式，画出它的大致图象并标注顶点及其坐标； （2）结合图象，回答下列问题： ①当1≤x≤4时，y 的取值范围是 ；②当m≤x≤m+3时，求y 的最大值（用含m 的代数式表示）；③是否存在实数m 、n （m≠n ），使得当m≤x≤n 时，m≤y≤n ？若存在，请求出m 、n ；若不存在，请说明理由．【答案】（1）y ＝x 2﹣4x+5，见解析；（2）①1≤y≤5，②当x ＝m+3时，y 有最大值为y＝m 2﹣+2m+2；当x ＝m 时，y 有最大值为y ＝m 2﹣4m+5，③存在，mn＝【解析】 【分析】（1）用待定系数法求出解析式，用描点法画出函数图象；（2）①根据函数图象找出横坐标由1到4的点的纵坐标的最大值与最小值，便可写出y 的取值范围； ②先求出对称轴x ＝﹣2b a ，分两种情况：﹣2b a ﹣m ≥m +3﹣（﹣2b a ）或﹣2ba﹣m ＜m +3﹣（﹣2ba），根据二次函数的性质求y 的最大值便可； ③利用已知可得图象过（a ，a ）点，进而得出a 的值，即可得出m ，n 的值． 【详解】（1）设二次函数的解析式为：y ＝ax 2+bx +c （a ≠0），则52932c a b c a b c =⎧⎪++=⎨⎪++=⎩， 解得，145a b c =⎧⎪=-⎨⎪=⎩，∴二次函数的解析式为：y ＝x 2﹣4x +5， 列表如下：描点、连线，（2）①由函数图象可知，当2,1x y ==最小时，当4,5x y ==最大时 ∴当1≤x ≤4时，1≤y ≤5， 故答案为：1≤y ≤5；②∵二次函数的解析式为：y ＝x 2﹣4x +5， ∴对称轴为x ＝2， 当2﹣m ≤m +3﹣2，即m ≥12时，则在m ≤x ≤m +3内，当x ＝m +3时，y 有最大值为y ＝x 2﹣4x +5＝（m +3）2﹣4（m +3）+5＝m 2﹣+2m +2； 当2﹣m ＞m +3﹣2，即m ＜12时，则在m ≤x ≤m +3内，当x ＝m 时，y 有最大值为y ＝x 2﹣4x +5＝m 2﹣4m +5；③由已知可得图象过（a ，a ）点， ∴a ＝a 2﹣4a +5， 解得，a 55± ∵当m ≤x ≤n 时，m ≤y ≤n ， ∴可以取m 55-n ＝552+．【点睛】本题是二次函数的综合题，主要考查了待定系数法求二次函数的解析式，画二次函数图象，由函数图象解决问题，后两问难度较大，关键是分情况讨论和根据特征点解题． 9．如图，抛物线经过()1,0A -，()3,0B ，30,2C ⎛⎫⎪⎝⎭三点．（1）求抛物线的解析式；（2）在抛物线的对称轴上有一点P ，使PA PC +的值最小，求点P 的坐标； （3）点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A ，C ，M ，N 四点构成的四边形为平行四边形？若存在，求点N 的坐标；若不存在，请说明理由． 【答案】（1）21322y x x =-++；（2）()1,1P ；（3）存在，点N 的坐标为32,2⎛⎫⎪⎝⎭，317,2⎛⎫+- ⎪⎝⎭，317,2⎛⎫- ⎪⎝⎭【解析】 【分析】（1）设抛物线的解析式为()20y ax bx c a =++≠，然后根据待定系数法进行求解；（2）根据点A 关于对称轴对称的点B 的坐标为(3,0)，连接BC 交对称轴直线于点P ，求出P 点坐标即可；（3）分点N 在x 轴下方或上方两种情况进行讨论． 【详解】解：（1）设抛物线的解析式为()20y ax bx c a =++≠，∵()1,0A -，()3,0B ，30,2C ⎛⎫⎪⎝⎭三点在抛物线上， ∴093032a b c a b c c ⎧⎪-+=⎪++=⎨⎪⎪=⎩， 解得，12132a b c ⎧=-⎪⎪=⎨⎪⎪=⎩，∴抛物线的解析式为：21322y x x =-++； （2）∵抛物线的解析式为21322y x x =-++，∴其对称轴为直线：12bx a=-=， 如图1所示，连接BC ，设直线BC 的解析式为()0y kx b k =+≠， ∵()3,0B ，30,2C ⎛⎫ ⎪⎝⎭， ∴3032k b b +=⎧⎪⎨=⎪⎩， 解得，1232k b ⎧=-⎪⎪⎨⎪=⎪⎩，∴直线BC 的解析式为1322y x =-+， 当1x =时，13122y =-+=， ∴()1,1P ；（3）存在，如图2所示， ①当点N 在x 轴上方时，∵抛物线的对称轴为直线1x =，30,2C ⎛⎫ ⎪⎝⎭， ∴132,2N ⎛⎫ ⎪⎝⎭；②当点N 在x 轴下方时，过点2N 作2N D x ⊥轴于点D ， ∴22AN D M CO ≅△△，∴232N D OC ==，即2N 点的纵坐标为32-， ∴2133222x x -++=-，解得，1x =+1x =-∴2312N ⎛⎫+-⎪⎝⎭，3312N ⎛⎫- ⎪⎝⎭，综上所述，点N 的坐标为32,2⎛⎫ ⎪⎝⎭，317,2⎛⎫+-⎪⎝⎭，317,2⎛⎫-- ⎪⎝⎭．【点睛】本题是二次函数与几何的综合题，考查了利用待定系数法求解函数的解析式，二次函数的对称轴，平行四边形的性质，全等三角形的性质，第（3）小题要注意进行分类讨论．10．如图，在平面直角坐标系中，抛物线2y x bx c =-++与x 轴交于(10)A -，，(30)B ，两点，与y 轴交于点C ．（1）直接写出抛物线的解析式为：；（2）点D 为第一象限内抛物线上的一动点，作DE x ⊥轴于点E ，交BC 于点F ，过点F 作BC 的垂线与抛物线的对称轴和y 轴分别交于点G ，H ，设点D 的横坐标为m ． ①求DF HF +的最大值；②连接EG ，若45GEH ∠=，求m 的值．【答案】（1）2y x 2x 3=-++；（2）①1124+；②1m =，95【解析】 【分析】（1）将点(10)A -，，(30)B ，代入抛物线2y x bx c =-++，求出b 、c 的值，继而求出抛物线解析式；（2）①先求出点C 的坐标，由待定系数法求出直线BC 的解析式，作FK y ⊥轴于点K ，可得： FH ==，由线段的和差可得：DF HF DE EF +=-+，代入数据得到二次函数，由二次函数的性质可知当m =，DF HF +有最大值； ②作GM y ⊥轴于点M ，记直线FH 与x 轴交于点N ，易知45EFH ENF ∠=∠=，由等角对等边可知：EN ＝EF ，OH ＝ON ，由抛物线的性质可得MG ＝1，继而可得HG，根据相似三角形的判定及其性质可得~EHG FHE ∆∆，HE HF HG HE=，代入数据可得22HE HG HF m =⋅=，在Rt OEH ∆中，由勾股定理可得22225129HE OE OH m m =+=-+，可得一元二次方程，继而解方程求解．【详解】（1）将点(10)A -，，(30)B ，代入抛物线2y x bx c =-++得： 01093b c b c=--+⎧⎨=-++⎩ 解得：23b c故抛物线的解析式为：2y x 2x 3=-++；（2）①当0x =时，2y x 2x 3=-++∴点(0,3)C ，又点(3,0)B ，BC ∴的解析式为：3y x =-+，3OC OB ==，45OBC OCB ∴∠=∠=，作FK y ⊥轴于点K ，又FH BC ⊥，45KFH KHF ∴∠=∠=，FH ∴==，2(23)(3)DF HF DE EF m m m ∴+=-+=-++--++，化简得：2(3DF HF m m +=-+，由题意有03m <<，且3232032(1)2++<-=<⨯-，10-<， ∴当322m +=时，DF HF +取最大值， DF HF +的最大值为232321162()(32)+++-++⨯= ②作GM y ⊥轴于点M ，记直线FH 与x 轴交于点N ，FK y ⊥轴，DE x ⊥轴，45KFH ∠=，45EFH ENF ∴∠=∠=，EF EN ∴=，45KHF ONH ∠=∠=，OH ON ∴=，2y x 2x 3=-++的对称轴为1x =，1MG =∴，22HG MG ==，45GEH ∠=GEH EFH ∴∠=∠，又∠EHF ＝∠GHE ，~EHG FHE ∴∆∆，HE HF HG HE∴=， 2222HE HG HF m m ∴=⋅=⋅=在Rt OEH ∆中，(3)23OH ON OE EN OE EF m m m ==-=-=--+=-，OE m =222222(23)5129HE OE OH m m m m ∴=+=+-=-+251292m m m ∴-+=，解得：1m =或95【点睛】本题考查一次函数与二次函数的综合题，还涉及到相似三角形的判定及其性质，等角对等边的性质和等边对等角的性质，考查学生的数形结合能力，解题的关键是熟练掌握一次函数与二次函数的性质．11．如图，直线112y x =-+与x 轴交于点A ，与y 轴交于点B ，抛物线2y x bx c =-++经过A 、B 两点．（1）求抛物线的解析式；（2）若P 是抛物线上一点，且P 点坐标为3,12⎛⎫ ⎪⎝⎭，点Q 为抛物线对称轴上一点，求QP QA +的最小值；（3）点N 为直线AB 上的动点，点M 为抛物线上的动点，当以点O 、B 、M 、N 为顶点的四边形是平行四边形时，求点M 的坐标．【答案】（1）2312y x x =-++；（2）QP ＋QA 5（3）满足条件的点M 的坐标为112,(12)2⎛⎫+-+ ⎪⎝⎭或112,(12)2⎛⎫--- ⎪⎝⎭或31,2⎛⎫ ⎪⎝⎭． 【解析】【分析】（1）先通过直线112y x =-+与x 轴交于点A ，与y 轴交于点B 计算出A 、B 点的坐标，再代入2y x bx c =-++计算即可；（2）根据对称性知A 点关于抛物线对称轴的对称点是1,02C ⎛⎫-⎪⎝⎭，连接PC ，则QP ＋QA 的最小值就是PC ，从而计算即可；（3）根据平行四边形的性质分为以OB 为边和对角线两种情况分类讨论计算．【详解】（1）∵直线112y x =-+与x 轴交于点A ，与y 轴交于点B ∴A （2，0），B （0，1）∵抛物线y＝－x2＋bx＋c经过A、B两点∴4201b cc-++=⎧⎨=⎩∴321 bc⎧=⎪⎨⎪=⎩∴抛物线解析式为2312y x x=-++（2）如解图①，由（1）知，抛物线解析式为2312y x x=-++∴抛物线的对称轴为直线34x=，抛物线与x轴的另一交点为1,02C⎛⎫-⎪⎝⎭∵点A与点C关于对称轴对称∴QP＋QA的最小值就是5PC=（3）①OB为平行四边形的边时，MN＝OB，MN∥OB∵点N在直线AB上∴设1,12N m m⎛⎫-+⎪⎝⎭∴23,12M m m m⎛⎫-++⎪⎝⎭∴2231112122MN m m m m m⎛⎫=-++--+=-+=⎪⎝⎭Ⅰ．－m 2＋2m ＝1解得，m ＝1 ∴31,2M ⎛⎫ ⎪⎝⎭Ⅱ．－m 2＋2m ＝－1 解得，12m∴11(12M ⎛⎫+-+ ⎪⎝⎭或11(12⎛⎫--- ⎪⎝⎭②当OB 为对角线时，OB 与MN 互相平分，交点为H ，∴OH ＝BH ，MH ＝NH ，∵B （0，1），O （0，0），∴10,2H ⎛⎫ ⎪⎝⎭， 设1,12N n n ⎛⎫-+ ⎪⎝⎭，23,12M d d d ⎛⎫-++ ⎪⎝⎭， ∴202131112222n d n d d +⎧=⎪⎪⎨-+-++⎪=⎪⎩，∴1(1d n ⎧=+⎪⎨=-⎪⎩或1(1d n ⎧=⎪⎨=-⎪⎩，∴11(12M ⎛⎫+-+ ⎪⎝⎭或11(12M ⎛⎫--- ⎪⎝⎭； 即：满足条件的点M的坐标为11(12⎛⎫+-+ ⎪⎝⎭或11(12⎛⎫--- ⎪⎝⎭或31,2⎛⎫ ⎪⎝⎭． 【点睛】本题考查二次函数与线段之和最短、平行四边形相结合，难度较大．数形结合的思维是解题关键．12．如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +2（a ≠0）与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，抛物线经过点D （﹣2，﹣3）和点E （3，2），点P 是第一象限抛物线上的一个动点．（1）求直线DE 和抛物线的表达式；（2）在y 轴上取点F （0，1），连接PF ，PB ，当四边形OBPF 的面积是7时，求点P 的坐标；（3）在（2）的条件下，当点P 在抛物线对称轴的右侧时，直线DE 上存在两点M ，N （点M 在点N 的上方），且MN ＝2Q 从点P 出发，沿P →M →N →A 的路线运动到终点A ，当点Q 的运动路程最短时，请直接写出此时点N 的坐标．【答案】（1）y ＝x ﹣1，y ＝12-x 2+32x +2；（2）P （2，3）或（32，258）；（3）N （12，12-）． 【解析】【分析】（1）将点D 、E 的坐标代入函数表达式，即可求解；（2）S 四边形OBPF ＝S △OBF +S △PFB ＝12×4×1+12×PH ×BO ，即可求解； （3）过点M 作A ′M ∥AN ，过作点A ′直线DE 的对称点A ″，连接PA ″交直线DE 于点M ，此时，点Q 运动的路径最短，即可求解．【详解】（1）将点D 、E 的坐标代入函数表达式得：34229322a b a b -=-+⎧⎨++=⎩，解得： 1232a b ⎧=-⎪⎪⎨⎪=⎪⎩，故抛物线的表达式为：y ＝12-x 2+32x +2， 同理可得直线DE 的表达式为：y ＝x ﹣1…①；（2）如图1，连接BF ，过点P 作PH ∥y 轴交BF 于点H ，将点FB 代入一次函数表达式，同理可得直线BF 的表达式为：y ＝14x -+1， 设点P （x ，213222x x -++），则点H （x ，14x -+1）， S 四边形OBPF ＝S △OBF +S △PFB ＝12×4×1+12×PH ×BO ＝2+2（213121224x x x -+++-）＝7，解得：x ＝2或32， 故点P （2，3）或（32，258）； （3）当点P 在抛物线对称轴的右侧时，点P （2，3），过点M 作A ′M ∥AN ，过作点A ′直线DE 的对称点A ″，连接PA ″交直线DE 于点M ，此时，点Q 运动的路径最短，∵MN ＝2，相当于向上、向右分别平移2个单位，故点A ′（1，2），A ′A ″⊥DE ，则直线A ′A ″过点A ′，则其表达式为：y ＝﹣x +3…②，联立①②得x ＝2，则A ′A ″中点坐标为（2，1），由中点坐标公式得：点A ″（3，0），同理可得：直线AP ″的表达式为：y ＝﹣3x +9…③，联立①③并解得：x ＝52，即点M （52，32），点M沿BD向下平移22个单位得：N（12，12-）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、图形的平移、面积的计算等，其中（3），通过平移和点的对称性，确定点Q运动的最短路径，是本题解题的关键．13．如图，直线y＝x+c与x轴交于点A（﹣4，0），与y轴交于点C，抛物线y＝﹣x2+bx+c 经过点A，C．（1）求抛物线的解析式；（2）已知点P是抛物线上的一个动点，并且点P在第二象限内，过动点P作PE⊥x轴于点E，交线段AC于点D．①如图1，过D作DF⊥y轴于点F，交抛物线于M，N两点（点M位于点N的左侧），连接EF，当线段EF的长度最短时，求点P，M，N的坐标；②如图2，连接CD，若以C，P，D为顶点的三角形与△ADE相似，求△CPD的面积．【答案】（1）y＝﹣x2﹣3x+4；（2）①点P坐标为（﹣2，6），点M、N的坐标分别为（3172--，2）、（3172-+，2）；②△CPD的面积为92或4．【解析】【分析】（1）将点A的坐标分别代入直线和抛物线表达式，即可求解；（2）①四边形DEOF为矩形，故：EF＝OD，当OD垂直于AC时，OD最小，点D 为AC的中点，其坐标为（﹣2，2），即可求解；②分△ADE∽△CDP、△ADE∽△PCD两种情况，求解即可．【详解】（1）将点A的坐标代入直线y＝x+c得：0＝﹣4+c，解得：c＝4，将点A 坐标代入抛物线表达式得：0＝﹣16﹣4b+4，解得：b ＝﹣3，故抛物线的表达式为：y ＝﹣x2﹣3x+4，故点A 、C 的坐标分别为（﹣4，0）、（0，4），将A 、C 点坐标代入一次函数表达式y ＝kx+b 得：044k b b =-+⎧⎨=⎩，解得14k b =⎧⎨=⎩， 则直线AC 的表达式为：y ＝x+4；（2）①∵四边形DEOF 为矩形，故：EF ＝OD ，当OD 垂直于AC 时，OD 最小（即EF 最小），∵OA ＝OC ，∴点D 为AC 的中点，其坐标为（﹣2，2），故点P 坐标为（﹣2，6），把点D 纵坐标代入二次函数表达式得：﹣x2﹣3x+4＝2，解得：x ＝32-±，故点M 、N 2）、，2）； ②当△ADE ∽△CDP 时，则∠CPD ＝90°，PC ＝PD ，则PC ∥x 轴，则点P 的纵坐标为4，则点P 坐标为（﹣3，4），点D 在直线AC ：y ＝x+4上，则点D 坐标为（﹣3，1），则PD ＝4﹣1＝3＝PC ，则S △CPD ＝12×PC•PD ＝92； 当△ADE ∽△PDC 时，同理可得：S △CPD ＝12×PD•CH ＝4，故：△CPD的面积为92或4．【点睛】本题考查的是二次函数知识的综合运用，涉及到三角形相似、矩形基本性质等知识点，其中（2），利用矩形性质OD＝EF，确定EF最小值，是本题的难点．14．已知．在Rt△OAB中，∠OAB=90°，∠BOA=30°，OA=23，若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内，将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．（1）求经过点O，C，A三点的抛物线的解析式．（2）若点M是抛物线上一点，且位于线段OC的上方，连接MO、MC，问：点M位于何处时三角形MOC的面积最大？并求出三角形MOC的最大面积．（3）抛物线上是否存在一点P，使∠OAP=∠BOC？若存在，请求出此时点P的坐标；若不存在，请说明理由．【答案】（1）y=﹣x23x；（2）333⎝⎭33；（3）存在，3，53)或(3﹣7 3 )【解析】【分析】（1）根据折叠的性质可得OC=OA，∠BOC=∠BAO=30°，过点C作CD⊥OA于D，求出OD、CD，然后写出点C的坐标，再利用待定系数法求二次函数解析式解答；（2）求出直线OC的解析式，根据点M到OC的最大距离时，面积最大；平行于OC 的直线与抛物线只有一个交点，利用根的判别式求出m的值，利用锐角三角函数的定义求解即可；（3）分两种情况求出直线AP与y轴的交点坐标，然后求出直线AP的解析式，与抛物线解析式联立求解即可得到点P的坐标．【详解】解：（1）∵Rt △OAB 沿OB 折叠后，点A 落在第一象限内的点C 处，∴OC=OA=23，∠BOC=∠BAO=30°，∴∠AOC=30°+30°=60°， 过点C 作CD ⊥OA 于D ，则OD=12×33 3×3， 所以，顶点C 33），设过点O ，C ，A 抛物线的解析式为为y=ax 2+bx ，则223)33(23)30a b a b ⎧+=⎪⎨+=⎪⎩， 解得：13a b =-⎧⎪⎨=⎪⎩ ∴抛物线的解析式为y=﹣x 23；（2）∵C 3，3），∴直线OC 的解析式为：3y x =，设点M 到OC 的最大距离时，平行于OC 的直线解析式为3y x m =+，联立233y x m y x x⎧=+⎪⎨=-+⎪⎩， 消掉未知数y 并整理得，230x x m -+=，△=（32-4m=0，解得：m=34．∴230 4x+=，∴x=；∴点M到OC的最大距离=34×sin30°=313428⨯=；∵OC==∴13288MOCS∆=⨯⨯=；此时，M⎝⎭，最大面积为8；（3）∵∠OAP=∠BOC=∠BOA =30°，∴2=，∴直线AP与y轴的交点坐标为（0，2）或（0，﹣2），当直线AP经过点（0）、（0，2）时，解析式为2y=+，联立223y xy x⎧=-+⎪⎨=-+⎪⎩，解得11xy⎧=⎪⎨=⎪⎩22353xy⎧=⎪⎪⎨⎪=⎪⎩．所以点P53），当直线AP经过点（0）、（0，﹣2）时，解析式为2y x=-，联立223y xy x⎧=-+⎪⎨=-⎪⎩解得110x y ⎧=⎪⎨=⎪⎩2273x y ⎧=⎪⎪⎨⎪=-⎪⎩； 所以点P的坐标为（-73-）． 综上所述，存在一点P5373），使∠OAP=∠BOA ． 【点睛】本题是二次函数综合题型，主要利用了折叠的性质，待定系数法求二次函数解析式，联立两函数解析式求交点的方法，（2）判断出点M 到OC 的距离最大是，平行于OC 的直线与抛物线只有一个交点是解题的关键，（3）确定出直线AP 的解析式是解题的关键． 15．抛物线2y x bx c =-++ （b c ，为常数）与x 轴交于点()1,0x 和()2,0x 与y 轴交于点A ，点E 为抛物线顶点．（Ⅰ）当121,3x x =-=时，求点E ，点A 的坐标；（Ⅱ）①若顶点E 在直线y x =上时，用含有b 的代数式表示c ；②在①的前提下，当点A 的位置最高时，求抛物线的解析式；（Ⅲ）若11,0x b =->，当()1,0P 满足PA PE +值最小时，求b 的值．【答案】（Ⅰ）2y x 2x 3=-++；（Ⅱ）①21142c b b =-+；②214y x x =-++；（Ⅲ）3b =+【解析】【分析】（Ⅰ）当121,3x x =-=时，y=0，由二次函数的交点式即可求出解析式；（Ⅱ）①由题意得24(,)24b c b E +，代入直线y=x 中即可解答； ②表达出211(0,)42A b b -+，根据二次函数的性质可知，当b=1时，点A 在最高点，即可得到二次函数解析式；（Ⅲ）将（-1,0）代入得到c=b+1，表达出2(2)(,)24b b E +， A （0，b+1）,求出点E 关于x 轴的对称点2(2)(,)24b b E +'-，根据当()1,0P 满足PA PE +值最小时，则此时点P ，A ，E '三点共线，求出直线AP 的解析式，将点2(2)(,)24b b E +'-代入直线AP 的解析式即可求出b 的值．【详解】解：（Ⅰ）当121,3x x =-=时，y=0，∴(1)(3)y x x =-+-，∴2y x 2x 3=-++（Ⅱ）①∵点E 是抛物线2y x bx c =-++的顶点， ∴24(,)24b c b E +， ∵顶点E 在直线y x =上， ∴24=24b c b +， ∴21142c b b =-+， ②由①可知211(0,)42A b b -+， 21142c b b =-+，104-<， ∴当12112()4b =-=⨯-时，21142c b b =-+最大，即点A 是最高点， 此时14c =， ∴214y x x =-++； （Ⅲ）∵抛物线经过（-1,0）,∴-1-b+c=0，∴c=b+1，∵24(,)24b c b E +，A （0，c ） ∴2(2)(,)24b b E +， A （0，b+1）, ∴点E 关于x 轴对称的点2(2)(,)24b b E +'-， ∵当()1,0P 满足PA PE +值最小时，则此时点P ，A ，E '三点共线，设过点A ，P 的直线为y=kx+t ，将点A （0，b+1），P （1，0）代入得10t b k t =+⎧⎨+=⎩，解得：11t b k b =+⎧⎨=--⎩， ∴y=(-b-1)x+b+1， 将2(2)(,)24b b E +'-代入得：2(2)(1)124b b b b +--++=-， 整理得：2680b b --=，解得：3b =3b =∵b ＞0，∴3b =+【点睛】本题考查了二次函数的图象及性质，掌握待定系数法求函数解析式，利用轴对称求最短距离是解题的关键．16．已知：抛物线)222y kx k x k k =++++经过坐标原点． （1）求抛物线的解析式和顶点B 的坐标；（2）设点A 是抛物线与x 轴的另一个交点且A 、C 两点关于y 轴对称，试在y 轴上确定一点P ，使PA+PB 最短，并求出点P 的坐标；（3）过点A 作AD ∥BP 交y 轴于点D ，求到直线AP 、AD 、CP 距离相等的点的坐标．【答案】（1）抛物线的解析式是y ＝﹣x 2，顶点B ，3）；（2）点P 的坐标是（0，2）；（3）到直线AP 、AD 、CP 距离相等的点的坐标是（0，0）和（2）．【解析】【分析】（1）根据抛物线经过原点求出k 的值，即可求出解析式，在求顶点坐标即可； （2）先找出P 的位置，再求直线BC 的解析式，再求点P 的坐标即可；（3）先求得y 轴是∠APC 的角平分线，x 轴是∠DAP 的角平分线，交点符合要求，∠DAP的外角∠EAP 的平分线和∠CPA 的外角∠FPA 的平分线的交点M 也符合要求.【详解】解：（1）∵抛物线2223(2)y kx k x k k =++++经过坐标原点，∴k 2+k ＝0，解得：k ＝0（舍去），k ＝﹣1，∴抛物线的解析式是y ＝﹣x 2+23x ， ∴y ＝﹣x 2+23x ，＝﹣（x ﹣3）2+3，∴顶点B 的坐标是（3，3），答：抛物线的解析式是y ＝﹣x 2+23x ，顶点B 的坐标是（3，3）；（2）当y ＝0时﹣x 2+23x ＝0，解得：x 1＝0，x 2＝23，∴A 的坐标是（23，0），A 关于y 轴的对称点C 的坐标是C （﹣23，0），设直线BC 的解析式是y ＝kx+b ，把B 33），C （﹣30）代入得：33k b 03k b⎧=+⎪⎨=-+⎪⎩，解得：32kb⎧=⎪⎨⎪=⎩，∴直线BC的解析式是y＝33x+2，当x＝0时，y＝2，∴点P的坐标是（0，2），答：点P的坐标是（0，2）．（3）∵A、C关于y轴对称，P在Y轴上，∴AP＝CP，∵∠CAP＝∠ACP，x轴⊥y轴，∴y轴是∠APC的角平分线，即y轴上任意一点到AP、CP的距离都相等，∵AD∥PC，∴∠DAC＝∠ACP，∴∠DAC＝∠CAP，∴x轴是∠DAP的角平分线，即x轴上任意一点到AP、AD的距离都相等，∴x轴与y轴的交点O到AP、AD、CP距离相等，∴点的坐标是（0，0），如图，∠DAP的外角∠EAP的平分线和∠CPA的外角∠FPA的平分线的交点M也符合要求，根据作图条件能得到矩形MAOP，即点M的坐标是（3，2），到直线AP、AD、CP距离相等的点的坐标是（0，0）和（32），答：到直线AP、AD、CP距离相等的点的坐标是（0，0）和（23，2）．【点睛】本题考查了二次函数的综合题：熟练掌握待定系数法求函数解析式，最值问题，角平分线的性质. 找出PA+PB有最小值的条件是解题的关键．17．已知，如图，二次函数y＝﹣x2+bx+c的图象经过点A(﹣1，0)，B(3，0)，点E为二次函数第一象限内抛物线上一动点，EH⊥x轴于点H，交直线BC于点F，以EF为直径的圆⊙M与BC交于点R.(1)求这个二次函数关系式.(2)当△EFR周长最大时.①求此时点E点坐标及△EFR周长.②点P为⊙M上一动点，连接BP，点Q为BP的中点，连接HQ，求HQ的最大值.【答案】(1)y＝﹣x2+2x+3；(2)①E(32，154)，周长为94+942；②HQ的最大值大为：365 16+9 16.【解析】【分析】(1)用交点式函数表达式，即可求解；(2)①证明△ERF为等腰直角三角形，当△EFR周长最大时，EF最长，EF＝﹣m2+3m，即可求解；②HQ＝12OP，利用OP≤OM+PM＝365988+，即可求解.【详解】(1)用交点式函数表达式得：y＝﹣(x+1)(x﹣3)＝﹣x2+2x+3；(2)①由（1）知C（0,3），∴OC=OB=3，∴∠OBC=45︒，。