四边形中的最值问题专题

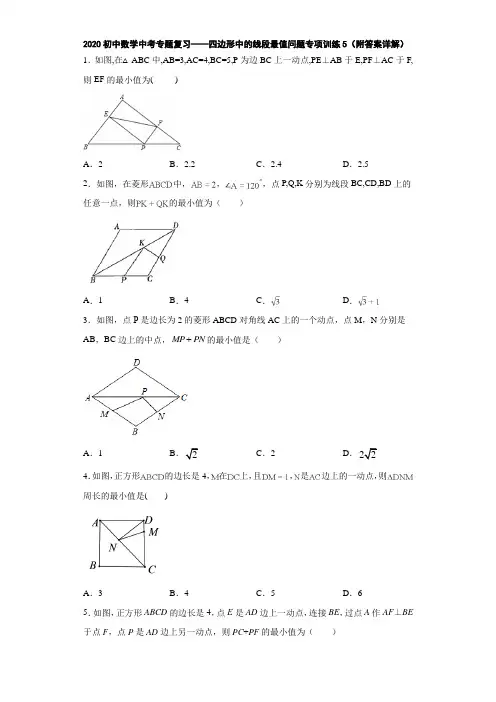
专题9.8 四边形中的最值问题专项训练（30道）【苏科版】考卷信息：本套训练卷共30题，选择15题，填空15题，题型针对性较高，覆盖面广，选题有深度，可强化学生对四边形中最值问题模型的记忆与理解！1．（2021春•德阳期末）如图，将矩形ABCD放置在平面直角坐标系的第一象限内，使顶点A，B分别在x轴、y轴上滑动，矩形的形状保持不变，若AB＝2，BC＝1，则顶点C 到坐标原点O的最大距离为（）A．1+√2B．1+√3C．3D．√5【解题思路】取AD的中点E，连接OE，CE，OC，求得CE=√2，OE＝1，再根据OC ≤CE+OE＝1+√2，即可得到点C到原点O距离的最大值是1+√2．【解答过程】解：如图，取AB的中点E，连接OE，CE，OC，∵∠AOB＝90°，∴Rt△AOB中，OE=12AB＝1，又∵∠ABC＝90°，AE＝BE＝CB＝1，∴Rt△CBE中，CE=√12+12=√2，又∵OC≤CE+OE＝1+√2，∴OC的最大值为1+√2，即点C到原点O距离的最大值是1+√2，故选：A．2．（2021春•西岗区期末）如图，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则AM的最小值是（）A．2.4B．2C．1.5D．1.2【解题思路】AM=12EF=12AP，所以当AP最小时，AM最小，根据垂线段最短解答．【解答过程】解：由题意知，四边形AFPE是矩形，∵点M是矩形对角线EF的中点，则延长AM应过点P，∴当AP为直角三角形ABC的斜边上的高时，即AP⊥BC时，AM有最小值，此时AM=12AP，由勾股定理知BC=√32+42=5，∵S△ABC=12AB•AC=12BC•AP，∴AP=3×45=125，∴AM=12AP=65=1.2，故选：D．3．（2021春•龙口市期末）如图，在边长为6的正方形ABCD中，点P为对角线AC上一动点，PE⊥AB于E，PF⊥BC于F，则EF的最小值为（）A．6√2B．3√2C．4D．3【解题思路】连接BP，根据PE⊥AB，PF⊥BC得到四边形PEBF为矩形，得EF＝BP，BP最短时即BP⊥AC，即可求解．【解答过程】解：连接BP，如图，，∵四边形ABCD是正方形，∴∠ABC＝90°，AB＝BC＝6，∵PE⊥AB，PF⊥BC，∴四边形PEBF为矩形，∴EF＝BP，当BP⊥AC，BP最短，在Rt△BPC中，BP＝PC，BC＝6，根据勾股定理可解得BP＝3√2，∴EF得最小值为3√2．故选：B．4．（2021春•重庆期末）如图，以边长为4的正方形ABCD的中心O为端点，引两条互相垂直的射线，分别与正方形的边交于E、F两点，则线段EF的最小值是（）A．√2B．2C．√8D．4【解题思路】根据正方形的性质得到∠EAO＝∠FDO＝45°，AO＝DO，证得△AOE≌△DOF，根据全等三角形的性质得到OE＝OF，求出OE的范围，借助勾股定理即可解决问题．【解答过程】解：∵四边形ABCD为正方形，∴∠EAO＝∠FDO＝45°，AO＝DO；∵∠EOF＝90°，∠AOD＝90°，在△AOE 与△DOF 中，{∠EAO =∠FDO AO =DO ∠AOE =∠DOF，∴△AOE ≌△DOF （ASA ），∴OE ＝OF （设为λ）；∴△EOF 是等腰直角三角形，由勾股定理得：EF 2＝OE 2+OF 2＝2λ2；∴EF =√2OE =√2λ，∵正方形ABCD 的边长是4，∴OA ＝2√2，O 到AB 的距离等于2（O 到AB 的垂线段的长度）， 由题意可得：2≤λ≤2√2，∴2√2≤EF ≤4．所以线段EF 的最小值为2√2．故选：C ．5．（2021春•马鞍山期末）如图，在菱形ABCD 中，∠B ＝45°，BC =2√3，E ，F 分别是边CD ，BC 上的动点，连接AE 和EF ，G ，H 分别为AE ，EF 的中点，连接GH ，则GH 的最小值为（ ）A ．√3B ．√62C ．√63D ．1 【解题思路】连接AF ，利用三角形中位线定理，可知GH =12AF ，求出AF 的最小值即可解决问题．【解答过程】解：连接AF ，如图所示：∵四边形ABCD 是菱形， ∴AB ＝BC ＝2√3，∵G ，H 分别为AE ，EF 的中点，∴GH 是△AEF 的中位线，∴GH =12AF ，当AF ⊥BC 时，AF 最小，GH 得到最小值，∵∠B ＝45°，∴△ABF 是等腰直角三角形，∴AF =√22AB =√22×2√3=√6，∴GH =√62，即GH 的最小值为√62， 故选：B ．6．（2021春•潜山市期末）如图，点E 是边长为8的正方形ABCD 的对角线BD 上的动点，以AE 为边向左侧作正方形AEFG ，点P 为AD 的中点，连接PG ，在点E 运动过程中，线段PG 的最小值是（ ）A ．2B ．√2C ．2√2D ．4√2【解题思路】连接DG ，可证△AGD ≌△AEB ，得到G 点轨迹，利用点到直线的最短距离进行求解．【解答过程】解：连接DG ，如图，，∵四边形ABCD 、四边形AEFG 均为正方形，∴∠DAB ＝∠GAE ＝90°，AB ＝AD ，AG ＝AE ，∵∠GAD+∠DAE＝∠DAE+∠AE，∴∠GAD＝∠BAE，∵AB＝AD，AG＝AE，∴△AEB≌△AGD（SAS），∴∠PDG＝∠ABE＝45°，∴G点轨迹为线段DH，当PG⊥DH时，PG最短，在Rt△PDG中，∠PDG＝45°，P为AD中点，DP＝4，设PG＝x，则DG＝x，由勾股定理得，x2+x2＝42，解得x=2√2，故选：C．7．（2021春•蚌埠期末）如图，矩形ABCD中，AB：AD＝2：1，点E为AB的中点，点F 为EC上一个动点，点P为DF的中点，连接PB．若PB的最小值为5√2，则AD的值为（）A．5B．6C．7D．8【解题思路】F点在运动时，P点轨迹为平行EC的线段，BP最短为点到直线的最短距离．【解答过程】解：当F运动时，P点轨迹为GH，如图，，∵AB：AD＝2：1，∴AD＝AE＝EB＝BC，∴∠ADE＝∠DEA＝∠CEB＝∠ECB＝45°，∴∠DEC＝90°，BP的最距离为BP⊥GH时，此时P点与H点重合，F点与C点重合．∵H为CD中点，∴CH＝CB，∠GHB＝90°，在Rt△HCB中，BH＝5√2，∴CH＝CB＝5，故选：A．8．（2021春•南安市期末）如图，在矩形ABCD中，AB＝4，AD＝6，点P在AD上，点Q 在BC上，且AP＝CQ，连接CP，QD，则PC+QD的最小值为（）A．8B．10C．12D．20【解题思路】连接BP，则PC+QD的最小值转化为PC+PB的最小值，在BA的延长线上截取AE＝AB＝4，连接PE、CE，则PC+QD＝PC+PB＝PC+PE≥CE，再根据勾股定理求解即可．【解答过程】解：如图，连接BP，在矩形ABCD中，AD∥BC，AD＝BC＝6，∵AP＝CQ，∴AD﹣AP＝BC﹣CQ，∴DP＝QB，DP∥BQ，∴四边形DPBQ是平行四边形，∴PB∥DQ，PB＝DQ，则PC+QD＝PC+PB，则PC+QD的最小值转化为PC+PB的最小值，在BA的延长线上截取AE＝AB＝4，连接PE，则BE＝2AB＝8，∵P A⊥BE，∴P A是BE的垂直平分线，∴PB＝PE，∴PC+PB＝PC+PE，连接CE，则PC+QD＝PC+PB＝PC+PE≥CE，∴CE=√BE2+BC2=√82+62=10，∴PC+PB的最小值为10，即PC+QD的最小值为10，故选：B ．9．（2021春•连云港期末）如图，线段AB 的长为8，点D 在AB 上，△ACD 是边长为3的等边三角形，过点D 作与CD 垂直的射线DP ，过DP 上一动点G （不与D 重合）作矩形CDGH ，记矩形CDGH 的对角线交点为O ，连接OB ，则线段BO 的最小值为（ ）A ．5B ．4C ．4√3D ．5√3【解题思路】连接AO ，根据矩形对角线相等且互相平分得：OC ＝OD ，再证明△ACO ≌△ADO ，则∠OAB ＝30°；点O 一定在∠CAB 的平分线上运动，根据垂线段最短得：当OB ⊥AO 时，OB 的长最小，根据直角三角形30度角所对的直角边是斜边的一半得出结论．【解答过程】解：连接AO ，∵四边形CDGH 是矩形，∴CG ＝DH ，OC =12CG ，OD =12DH ，∴OC ＝OD ，∵△ACD 是等边三角形，∴AC ＝AD ，∠CAD ＝60°，在△ACO 和△ADO 中，{AC =AD AO =AO CO =DO， ∴△ACO ≌△ADO （SSS ），∴∠OAB＝∠CAO＝30°，∴点O一定在∠CAB的平分线上运动，∴当OB⊥AO时，OB的长度最小，∵∠OAB＝30°，∠AOB＝90°，∴OB=12AB=12×8＝4，即OB的最小值为4．故选：B．10．（2021春•惠山区期中）如图，平面内三点A、B、C，AB＝5，AC＝4，以BC为对角线作正方形BDCE，连接AD，则AD的最大值是（）A．5B．9C．9√2D．92√2【解题思路】如图将△BDA绕点D顺时针旋转90°得到△CDM．由旋转不变性可知：AB＝CM＝5，DA＝DM．∠ADM＝90°，得出△ADM是等腰直角三角形，推出AD=√22AM，当AM的值最大时，AD的值最大，根据三角形的三边关系求出AM的最大值即可解决问题．【解答过程】解：如图，将△BDA绕点D顺时针旋转90°得到△CDM，由旋转不变性可知：AB＝CM＝5，DA＝DM，∠ADM＝90°，∴△ADM是等腰直角三角形，∴AD=√22AM，∴当AM的值最大时，AD的值最大，∵AM≤AC+CM，∴AM≤9，∴AM 的最大值为9， ∴AD 的最大值为9√22．故选：D ．11．（2021春•邗江区期末）如图，以边长为4的正方形ABCD 的中心O 为端点，引两条相互垂直的射线，分别与正方形的边交于E 、F 两点，则线段EF 的最小值为（ ）A ．2B ．4C ．√2D ．2√2【解题思路】如图，作辅助线；证明△AOE ≌△DOF ，进而得到OE ＝OF ，此为解决该题的关键性结论；求出OE 的范围，借助勾股定理即可解决问题．【解答过程】解：如图，连接EF ，∵四边形ABCD 为正方形，∴∠EAO ＝∠FDO ＝45°，AO ＝DO ；∵∠EOF ＝90°，∠AOD ＝90°，∴∠AOE ＝∠DOF ；在△AOE 与△DOF 中，{∠EAO =∠FDO AO =DO ∠AOE =∠DOF，∴△AOE ≌△DOF （ASA ），∴OE ＝OF （设为λ）；∴△EOF 是等腰直角三角形，由勾股定理得：EF 2＝OE 2+OF 2＝2λ2；∴EF =√2OE =√2λ，∵正方形ABCD 的边长是4，∴OA＝2√2，O到AB的距离等于2（O到AB的垂线段的长度），由题意可得：2≤λ≤2√2，∴2√2≤EF≤4．所以线段EF的最小值为2√2．故选：D．12．（2021•宁蒗县模拟）如图，菱形ABCD的的边长为6，∠ABC＝60°，对角线BD上有两个动点E、F（点E在点F的左侧），若EF＝2，则AE+CF的最小值为（）A．2√10B．4√2C．6D．8【解题思路】作AM⊥AC，连接CM交BD于F，根据菱形的性质和等边三角形的判定和性质以及勾股定理解答即可．【解答过程】解：如图，连接AC，作AM⊥AC，使得AM＝EF＝2，连接CM交BD于F，∵AC，BD是菱形ABCD的对角线，∴BD⊥AC，∵AM⊥AC，∴AM∥BD，∴AM∥EF，∵AM＝EF，AM∥EF，∴四边形AEFM是平行四边形，∴AE＝FM，∴AE+CF＝FM+FC＝CM，根据两点之间线段最短可知，此时AE+FC最短，∵四边形ABCD是菱形，AB＝6，∠ABC＝60°∴BC＝AB，∴△ABC是等边三角形，∴AC＝AB＝6，在Rt△CAM中，CM=√AM2+AC2=√22+62=2√10∴AE+CF的最小值为2√10．故选：A．13．（2021春•宜兴市期中）如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点，且BE＝CF，连接BF、DE，则BF+DE的最小值为（）A．√12B．√20C．√48D．√80【解题思路】连接AE，利用△ABE≌△BCF转化线段BF得到BF+DE＝AE+DE，则通过作A点关于BC对称点H，连接DH交BC于E点，利用勾股定理求出DH长即可．【解答过程】解：连接AE，如图1，∵四边形ABCD是正方形，∴AB＝BC，∠ABE＝∠BCF＝90°．又BE＝CF，∴△ABE≌△BCF（SAS）．∴AE＝BF．所以BF+DE最小值等于AE+DE最小值．作点A关于BC的对称点H点，如图2，连接BH，则A、B、H三点共线，连接DH，DH与BC的交点即为所求的E点．根据对称性可知AE＝HE，所以AE+DE＝DH．在Rt△ADH中，DH=√AH2+AD2=√82+42=√80，∴BF+DE最小值为√80．故选：D．14．（2021春•重庆期末）如图，矩形ABCD中，AB＝2√3，BC＝6，P为矩形内一点，连接P A，PB，PC，则P A+PB+PC的最小值是（）A．4√3+3B．2√21C．2√3+6D．4√5【解题思路】将△BPC绕点C逆时针旋转60°，得到△EFC，连接PF、AE、AC，则AE的长即为所求．【解答过程】解：将△BPC绕点C逆时针旋转60°，得到△EFC，连接PF、AE、AC，则AE的长即为所求．由旋转的性质可知：△PFC是等边三角形，∴PC＝PF，∵PB＝EF，∴P A+PB+PC＝P A+PF+EF，∴当A、P、F、E共线时，P A+PB+PC的值最小，∵四边形ABCD是矩形，∴∠ABC＝90°，∴tan∠ACB=ABBC=√33，∴∠ACB＝30°，AC＝2AB＝4√3，∵∠BCE＝60°，∴∠ACE＝90°，∴AE=√(4√3)2+62=2√21，故选：B．15．（2021•江阴市模拟）如图，在边长为6的正方形ABCD中，点E、F、G分别在边AB、AD、CD上，EG与BF交于点I，AE＝2，BF＝EG，DG＞AE，则DI的最小值等于（）A．√5+3B．2√13−2C．2√10−65D．2√2+3【解题思路】过点E作EM⊥CD于点M，取BE的中点O，连接OI、OD，根据HL证明Rt△BAF≌Rt△EMG，可得∠ABF＝∠MEG，所以再证明∠EPF＝90°，由直角三角形斜边上的中线等于斜边的一半可得OI=12BE，由OD﹣OI≤DI，当O、D、I共线时，DI有最小值，即可求DI的最小值．【解答过程】解：如图，过点E作EM⊥CD于点M，取BE的中点O，连接OI、OD，∵四边形ABCD是正方形，∴AB＝AD，∠A＝∠D＝∠DME＝90°，AB∥CD，∴四边形ADME是矩形，∴EM＝AD＝AB，∵BF＝EG，∴Rt△BAF≌Rt△EMG（HL），∴∠ABF＝∠MEG，∠AFB＝∠EGM，∵AB∥CD∴∠MGE＝∠BEG＝∠AFB∵∠ABF+∠AFB＝90°∴∠ABF+∠BEG＝90°∴∠EIF＝90°，∴BF⊥EG；∵△EIB是直角三角形，∴OI=12BE，∵AB＝6，AE＝2，∴BE＝6﹣2＝4，OB＝OE＝2，∵OD﹣OI≤DI，∴当O、D、I共线时，DI有最小值，∵IO=12BE＝2，∴OD=√AD2+AO2=2√13，∴ID＝2√13−2，即DI的最小值为2√13−2，故选：B．16．如图，菱形ABCD的两条对角线长分别为AC＝6，BD＝8，点P是BC边上的一动点，则AP的最小值为 4.8．【解题思路】由垂线段最短，可得AP⊥BC时，AP有最小值，由菱形的性质和勾股定理可求BC的长，由菱形的面积公式可求解．【解答过程】解：设AC与BD的交点为O，∵点P是BC边上的一动点，∴AP⊥BC时，AP有最小值，∵四边形ABCD是菱形，∴AC⊥BD，AO＝CO=12AC＝3，BO＝DO=12BD＝4，∴BC=√OB2+OC2=√42+32=5，∵S菱形ABCD=12×AC×BD＝BC×AP，∴AP=245=4.8，故答案为：4.8．17．（2021春•椒江区期末）如图，矩形ABCD中，AB＝8，AD＝6，连接BD，E为BD上一动点，P为CE中点，连接P A，则P A的最小值是2√13．【解题思路】P点运动轨迹为△CDB的中位线，即求A点到这条中位线的最短距离．【解答过程】解：当点E运动时，P点轨迹为△CBD中位线GH，如图，，∵点A到直线GH的最短距离为AF，但是E点在运动中，P点轨迹为GH，∴点A到线段GH的最短距离为AG，∵G为CD中点，∴DG＝4，在Rt △ADG 中，AD ＝6，DG ＝4， ∴AG =√62+42=2√13．故答案为2√13．18．（2021春•宁德期末）如图，在矩形ABCD 中，AB ＝4，AD ＝3，点E 是CD 上一个动点，点F ，G 分别是AB ，AE 的中点，则线段FG 的最小值是 32 ．【解题思路】连接BE ，可得FG 是△ABE 的中位线，要使线段FG 最小，需BE 最小，当点E 与点C 重合时，BE 最小为3，进而可得线段FG 的最小值．【解答过程】解：如图，连接BE ，∵点F ，G 分别是AB ，AE 的中点，∴FG 是△ABE 的中位线，∴FG =12BE ，要使线段FG 最小，需BE 最小，当点E 与点C 重合时，BE 最小为3，则线段FG 的最小值是32． 故答案为：32． 19．（2021春•东海县期末）如图，在菱形ABCD 中，AC ＝24，BD ＝10，对角线交于点O ，点E 在AD 上，且DE =14AD ，点F 是OB 的中点，点G 为对角线AC 上的一动点，则GE ﹣GF 的最大值为 134 ．【解题思路】由菱形的性质可得AO ＝CO ＝12，BO ＝DO ＝5，AC ⊥BD ，在Rt △AOD 中，由勾股定理可求AD 的长，作点F 关于AC 的对称点F '，连接GF '，取AD 中点H ，连接OH ，可得GF ＝GF '，OF ＝OF '，则GE ﹣GF ＝GE ﹣GF '≤EF '，即当点G 在EF '的延长线时，GE ﹣GF 有最大值为EF '的长，由直角三角形的性质和三角形中位线定理可求解．【解答过程】解：∵四边形ABCD 是菱形，∴AO ＝CO ＝12，BO ＝DO ＝5，AC ⊥BD ， ∴AD =√AO 2+DO 2=√144+25=13，如图，作点F 关于AC 的对称点F '，连接GF '，取AD 中点H ，连接OH ，∵AC ⊥BD ，点H 是AD 中点，∴OH ＝HD =12AD =132，∵点F 与点F '关于AC 对称，∴GF ＝GF '，OF ＝OF '，∴GE ﹣GF ＝GE ﹣GF '≤EF '，∴当点G 在EF '的延长线时，GE ﹣GF 有最大值为EF '的长，∵DE =14AD ，HD =12AD ，∴DE ＝EH ，∵点F 是OB 的中点，∴OF =12OB ＝OF '=12DO ，∴EF '=12OH =134，故答案为：134．20．（2021•淄博）两张宽为3cm 的纸条交叉重叠成四边形ABCD ，如图所示．若∠α＝30°，则对角线BD 上的动点P 到A ，B ，C 三点距离之和的最小值是 6√2cm ．【解题思路】作DE⊥BC于E，解直角三角形求得AB＝BC＝6cm，把△ABP绕点B逆时针旋转60°得到△A'BP′，由旋转的性质，A′B＝AB＝6cm，BP′＝BP，A'P′＝AP，∠P′BP＝60°，A'BA＝60°，所以△P′BP是等边三角形，根据两点间线段距离最短，可知当P A+PB+PC＝A'C时最短，连接A'C，利用勾股定理求出A'C的长度，即求得点P 到A，B，C三点距离之和的最小值．【解答过程】解：如图，作DE⊥BC于E，把△ABP绕点B逆时针旋转60°得到△A'BP′，∵∠α＝30°，DE＝3cm，∴CD＝2DE＝6cm，同理：BC＝AD＝6cm，由旋转的性质，A′B＝AB＝CD＝6m，BP′＝BP，A'P′＝AP，∠P′BP＝60°，∠A'BA ＝60°，∴△P′BP是等边三角形，∴BP＝PP'，∴P A+PB+PC＝A'P′+PP'+PC，根据两点间线段距离最短，可知当P A+PB+PC＝A'C时最短，连接A'C，与BD的交点即为P点，即点P到A，B，C三点距离之和的最小值是A′C．∵∠ABC＝∠DCE＝∠α＝30°，∠A′BA＝60°，∴∠A′BC＝90°，∴A′C=√A′B2+BC2=√62+62=6√2（cm），因此点P到A，B，C三点距离之和的最小值是6√2cm，故答案为6√2cm．21．（2021春•龙岩期末）如图，正三角形ABC与正方形CDEF的顶点B，C，D三点共线，动点P沿着CA由C向A运动．连接EP，若AC＝10，CF＝8．则EP的最小值是4√3+4．【解题思路】过点E作EP⊥AC，交FC于点G，当EP⊥AC时，EP取得最小值，然后根据含30度角的直角三角形列式计算即可求出EP的最小值．【解答过程】解：如图，过点E作EP⊥AC，交FC于点G，当EP⊥AC时，EP取得最小值，∵正三角形ABC与正方形CDEF的顶点B，C，D三点共线，∴∠ACB＝60°，∠FCD＝90°，∴∠ACF＝30°，∴∠CGP＝∠EGF＝60°，∵∠F＝90°，∴∠FEG＝30°，设PG＝x，则CG＝2x，∴FG＝CF﹣CG＝8﹣2x，∴EG＝2FG＝2（8﹣2x），∵FG=√33EF，∴8﹣2x ＝8×√33， ∴x ＝4−4√33，∴EP ＝EG +PG ＝2（8﹣2x ）+x ＝16﹣3x ＝4√3+4．故答案为：4√3+4．22．（2021春•茅箭区校级期末）如图，已知线段AB ＝12，点C 在线段AB 上，且△ACD是边长为4的等边三角形，以CD 为边在CD 的右侧作矩形CDEF ，连接DF ，点M 是DF 的中点，连接MB ，则线段MB 的最小值为 6 ．【解题思路】连接AM 、CM 、EM ，根据四边形CDEF 是矩形，和△ACD 是等边三角形，证明△ADM ≌△ACM ，从而求出∠CAM ＝30°，当BM ⊥AM 时，MB 有最小值，然后用含有30°角的直角三角形的性质求出MB ．【解答过程】解：连接AM 、CM 、EM ，如图：∵矩形CDEF ，M 是DF 的中点，∴C 、M 、E 共线，∴DM =12DF =12CE ＝CM ，∵△ACD 是等边三角形，∴∠DAC ＝60°，AD ＝AC ，在△ADM 和△ACM 中，{AD =AC DM =CM AM =AM，∴△ADM ≌△ACM （SSS ），∴∠DAM ＝∠CAM ，∵∠DAC ＝60°，∴∠CAM ＝30°，∴当BM ⊥AM 时，MB 有最小值，此时，BM =12AB =12×12＝6， 故答案为：6．23．（2021•北仑区二模）如图，△ABC 的边AB ＝3，AB 边上的中线CM ＝1，分别以AC ，BC 为边向外作正方形ACGH 与正方形BCDE ，连接GD ，取GD 中点N ．则点N 到线段AB 的距离最大值为 52 ．【解题思路】当GD ∥AB 时，N 点到AB 的距离最大，则AC ＝BC ，∴N 、C 、M 三点共线且MN ⊥AB ，通过证明△AMC ≌△GOC ，可以求出AM ，然后再证明出OCNG 是矩形，从而求出MN ．【解答过程】解：∵点N 到AB 的距离介于G 、D 到AB 的距离之间，∴当GD ∥AB 时，N 点到AB 的距离最大，则AC ＝BC ，∴N 、C 、M 三点共线且MN ⊥AB ，过点C 作CP ∥AB ，作GO ⊥CP ，O 为垂足，∵PC ∥AB ，∴∠PCA ＝∠CAM ，∠PCA +∠OCG ＝90°，∠OGC +∠OCG ＝90°，∴∠OGC ＝∠PCA ＝∠CAM ，在△AMC 和△GOC 中，{∠AMC =∠GOC ∠CAM =CGO AC =CG，∴△AMC ≌△GOC （AAS ），∴GO ＝AM =12AB =32，∵GO ⊥PC ，MN ⊥AB ，PC ∥AB ，∴PC ⊥MN ，MN ⊥GD ，∴四边形GDCN 是矩形，∴GO ＝NC ，MN ＝CM +CN ，∵CM ＝1，GO ＝NC =32，∴MN ＝1+32=52．故答案为：52． 24．（2021•眉山）如图，在菱形ABCD 中，AB ＝AC ＝10，对角线AC 、BD 相交于点O ，点M 在线段AC 上，且AM ＝3，点P 为线段BD 上的一个动点，则MP +12PB 的最小值是 7√32 ．【解题思路】过点P 作PE ⊥BC 于E ，由菱形的性质可得AB ＝BC ＝AC ＝10，∠ABD ＝∠CBD ，可证△ABC 是等边三角形，可求∠CBD ＝30°，由直角三角形的性质可得PE =12PB ，则MP +12PB ＝PM +PE ，即当点M ，点P ，点E 共线且ME ⊥BC 时，PM +PE 有最小值为ME ，由锐角三角函数可求解．【解答过程】解：如图，过点P 作PE ⊥BC 于E ，∵四边形ABCD 是菱形，AB ＝AC ＝10，∴AB ＝BC ＝AC ＝10，∠ABD ＝∠CBD ，∴△ABC 是等边三角形，∴∠ABC ＝∠ACB ＝60°，∴∠CBD ＝30°，∵PE ⊥BC ，∴PE =12PB ，∴MP +12PB ＝PM +PE ，∴当点M ，点P ，点E 共线且ME ⊥BC 时，PM +PE 有最小值为ME ，∵AM ＝3，∴MC ＝7，∵sin ∠ACB =ME MC =√32， ∴ME =7√32，∴MP +12PB 的最小值为7√32， 故答案为7√32． 25．（2021•海安市二模）如图，矩形ABCD 中，AB ＝2，BC ＝4，E 在边BC 上运动，M 、N 在对角线BD 上运动，且MN =√5，连接CM 、EN ，则CM +EN 的最小值为 115 ．【解题思路】先作C 点关于BD 的对称点F ，然后再把F 左移2个单位，下移1个单位，得到Q ，再过Q 作QE ⊥BC 于E ，交BD 于N ，连接BF ，过F 作FP ⊥BC 于P ，以B 为原点建立平面直角坐标系，求出F 的坐标，再求出Q 的坐标，即可得出答案．【解答过程】解：先作C 点关于BD 的对称点F ，然后再把F 左移2个单位，下移1个单位，得到Q ，再过Q 作QE ⊥BC 于E ，交BD 于N ，连接BF ，过F 作FP ⊥BC 于P ，以B 为原点建立平面直角坐标系，如图所示，∵AB ＝2＝CD ，BC ＝4，∴C （4，0），BF ＝BC ＝4， 由勾股定理得：BD =√BC 2+CD 2=√42+22=2√5，由三角形面积公式得：12×CR ×BD =12×BC ×CD ， 即CR =BC×CD BD =2√5=4√55， 即CF ＝2CR =8√55，由勾股定理得：BF 2﹣BP 2＝CF 2﹣CP 2，∴42﹣BP 2＝（8√55）2﹣（4﹣BP ）2， 解得：BP =125，∴FP =√42−(125)2=165， ∴F 的坐标是（125，165）， ∴Q 的坐标是（25，115），即CM +EN 的最小值为115， 故答案为：115．26．（2021•浙江自主招生）如图，正方形ABCD 的边长为1，点P 为边BC 上任意一点（可与B 点或C 点重合），分别过B 、C 、D 作射线AP 的垂线，垂足分别是B ′、C ′、D ′，则BB ′+CC ′+DD ′的最大值为 2 ，最小值为 √2 ．【解题思路】连接AC 、DP ，根据三角形的面积公式得出S △DPC ＝S △APC =12AP ×CC ′，根据S 正方形ABCD ＝S △ABP +S △ADP +S △DPC ，推出BB ′+DD ′+CC ′=2AP ，根据已知得出1≤AP ≤√2，代入求出即可．【解答过程】解：连接AC、DP，S正方形ABCD＝1×1＝1，由勾股定理得：AC=√12+12=√2，∵AB＝1，∴1≤AP≤√2，∵△DPC和△APC的边CP上的高DC＝AB，∴S△DPC＝S△APC=12AP×CC′，1＝S正方形ABCD＝S△ABP+S△ADP+S△DPC=12AP（BB′+DD′+CC′），BB′+DD′+CC′=2 AP，∵1≤AP≤√2，√2≤BB′+CC′+DD′≤2，故答案为：2，√2．27．（2021•乾县一模）如图，在菱形ABCD中，∠BAD＝120°，点E为边AB的中点，点P在对角线BD上且PE+P A＝6，则AB长的最大值为4√3．【解题思路】连接PC，CE，AC；由已知条件可以得出PE+PC＝PE+P A＝6≥CE（当P是AE与DB的交点时取等号），再利用等边三角形的性质得出CE=√32AB，进而求出AB长的最大值．【解答过程】解：连接PC，CE，AC，如图所示：∵四边形ABCD是菱形，∴AB＝BC，AP＝PC，∴PE+PC＝PE+P A＝6≥CE，∵∠DAB＝120°，∴∠ABC ＝60°，∴△ABC 是等边三角形，∵点E 为线段AB 的中点，∴AE ＝BE ，∴∠AEC ＝90°，∠BCE ＝30°，∴CE =√32BC =√32AB ≤6，所以AB ≤4√3，即AB 长的最大值是4√3，故答案为：4√3．28．（2021•寿光市二模）如图所示，四边形ABCD 中，AC ⊥BD 于点O ，AO ＝CO ＝4，BO＝DO ＝3，点P 为线段AC 上的一个动点．过点P 分别作PM ⊥AD 于点M ，作PN ⊥DC 于点N ．连接PB ，在点P 运动过程中，PM +PN +PB 的最小值等于 7.8 ．【解题思路】证四边形ABCD 是菱形，得CD ＝AD ＝5，连接PD ，由三角形面积关系求出PM +PN ＝4.8，得当PB 最短时，PM +PN +PB 有最小值，则当BP ⊥AC 时，PB 最短，即可得出答案．【解答过程】解：∵AO ＝CO ＝4，BO ＝DO ＝3，∴AC ＝8，四边形ABCD 是平行四边形，∵AC ⊥BD 于点O ，∴平行四边形ABCD 是菱形，AD =√AO 2+DO 2=√42+32=5，∴CD ＝AD ＝5，连接PD ，如图所示：∵S △ADP +S △CDP ＝S △ADC ，∴12AD •PM +12DC •PN =12AC •OD ，即12×5×PM +12×5×PN =12×8×3， ∴5×（PM +PN ）＝8×3，∴PM +PN ＝4.8，∴当PB 最短时，PM +PN +PB 有最小值，由垂线段最短可知：当BP ⊥AC 时，PB 最短，∴当点P 与点O 重合时，PM +PN +PB 有最小值，最小值＝4.8+3＝7.8，故答案为：7.8．29．（2021•河西区二模）已知正方形ABCD 的边长为2，EF 分别是边BC ，CD 上的两个动点，且满足BE ＝CF ，连接AE ，AF ，则AE +AF 的最小值为 2√5 ．【解题思路】连接DE ，作点A 关于BC 的对称点A ′，连接BA ′、EA ′，易得AE +AF ＝AE +DE ＝A 'E +DE ，当D 、E 、A ′在同一直线时，AE +AF 最小，利用勾股定理求解即可．【解答过程】解：连接DE ，作点A 关于BC 的对称点A ′，连接BA ′、EA ′，∵四边形ABCD 为正方形，∴AD ＝CD ＝BC ，∠ADC ＝∠BCD ＝90°，∵BE ＝CF ，∴DF ＝CE ，在△DCE 与△ADF 中，{DC =AD ∠BCD =∠ADC CE =DF，∴△DCE ≌△ADF （SAS ），∴DE ＝AF ，∴AE +AF ＝AE +DE ，作点A 关于BC 的对称点A ′，连接BA ′、EA ′，则AE ＝A ′E ，即AE +AF ＝AE +DE ＝A 'E +DE ，当D 、E 、A ′在同一直线时，AE +AF 最小，AA ′＝2AB ＝4，此时，在Rt △ADA ′中，DA ′=√22+42=2√5， 故AE +AF 的最小值为2√5．故答案为：2√5．30．（2021春•鹿城区校级期中）学习新知：如图1、图2，P 是矩形ABCD 所在平面内任意一点，则有以下重要结论：AP 2+CP 2＝BP 2+DP 2．该结论的证明不难，同学们通过勾股定理即可证明．应用新知：如图3，在△ABC 中，CA ＝4，CB ＝6，D 是△ABC 内一点，且CD ＝2，∠ADB ＝90°，则AB 的最小值为 4√3−2 ．【解题思路】以AD 、BD 为边作矩形ADBE ，连接CE 、DE ，由矩形的性质得出AB ＝DE ，由题意得CD 2+CE 2＝CA 2+CB 2，求出CE ＝4√3，当C 、D 、E 三点共线时，DE 最小，得出AB 的最小值＝DE 的最小值＝CE ﹣CD ＝4√3−2．【解答过程】解：以AD 、BD 为边作矩形ADBE ，连接CE 、DE ，如图所示：则AB ＝DE ，由题意得：CD 2+CE 2＝CA 2+CB 2，即22+CE 2＝42+62，解得：CE＝4√3，当C、D、E三点共线时，DE最小，∴AB的最小值＝DE的最小值＝CE﹣CD＝4√3−2；故答案为：4√3−2．。

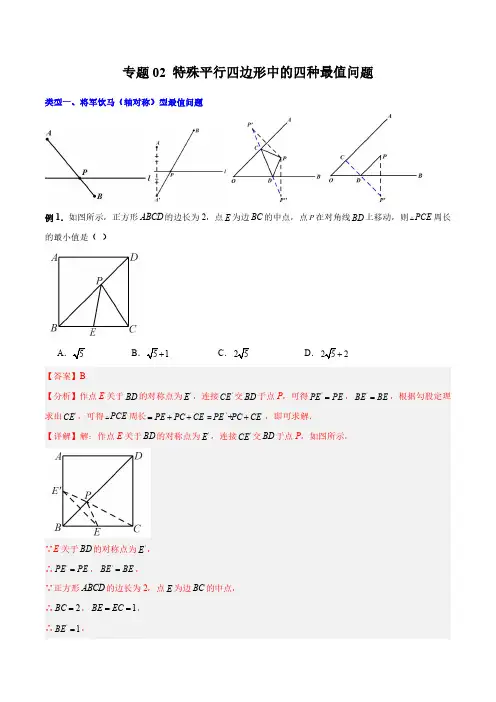
专题02特殊平行四边形中的四种最值问题类型一、将军饮马（轴对称）型最值问题A ．5B ．【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ，∴'PE PE =，'BE BE =，∵正方形ABCD 的边长为2，点A．0B．3【答案】C【分析】要使四边形APQE的周长最小，由于在BC边上确定点P、Q的位置，可在与BC交于一点即为Q点，过A点作后过G点作BC的平行线交DC的延长线于长度．∵四边形ABCD 是矩形，∴8BC AD ==，90D Ð=°，∠QCE ＝90°，∵2PQ =，∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ，∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形，∴GH ＝DF ＝6，∠H ＝90°,∵点E 是CD 中点，∴CE =2，∴EH ＝2+4＝6，∴∠GEH ＝45°，∴∠CEQ ＝45°，设BP ＝x ，则CQ ＝BC ﹣BP ﹣PQ ＝8﹣x ﹣2＝6﹣x ，在△CQE 中，∵∠QCE ＝90°，∠CEQ ＝45°，∴CQ ＝EC ，∴6﹣x ＝2，解得x ＝4．故选：C ．【点睛】本题考查了矩形的性质，轴对称﹣最短路线问题的应用，题目具有一定的代表性，是一道难度较大的题目，对学生提出了较高的要求．例3．如图，在矩形ABCD 中，26AB AD ==,，O 为对角线AC 的中点，点P 在AD 边上，且2AP =，点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度，延长∵GO AD'⊥，点O是AC的中点，∴132AG AD==，【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键．【变式训练1】如图，正方形ABCD的周长为24，P为对角线AC上的一个动点，E是CD的中点，则PE PD+的最小值为（）A ．35B ．32C ．6D ．5【答案】A 【详解】解：如图，连接BE ，设BE 与AC 交于点P'，∵四边形ABCD 是正方形，∴点B 与D 关于AC 对称，∴P'D =P'B ，∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时，PD +PE 最小，即为BE 的长度.∵正方形ABCD 的周长为24，∴直角△CBE 中，∠BCE =90°，BC =6，CE =12CD =3，∴226335BE =+=故选A.【变式训练2】如图，在矩形ABCD 中，AB ＝2，AD ＝3，动点P 满足S △PBC ＝14S 矩形ABCD ，则点P 到B ，C 两点距离之和PB +PC 的最小值为（）A 10B 13C 15D ．3【答案】B 【详解】解：设△PBC 中BC 边上的高是h ．∵S △PBC ＝14S 矩形ABCD ．∴12BC •h ＝14AB •AD ，∴h ＝12AB ＝1，∴动点P 在与BC 平行且与BC 的距离是1的直线l 上，如图，作B 关于直线l 的对称点E ，连接CE ，则CE 的长就是所求的最短距离．在Rt △BCE 中，∵BC ＝3，BE ＝BA ＝2，∴CE 2213+AB BC 即PB ＋PC 13故选：B ．【变式训练3】如图，在正方形ABCD 中，4AB =，AC 与BD 交于点O ，N 是AO 的中点，点M 在BC 边上，且3BM =，P 为对角线BD 上一点，则PM PN -的最大值为_____________．【答案】1【分析】作N 关于BD 的对称点E ，连接PE ，ME ，过点M 作MQ ⊥AC ，垂足为Q ，可判定当点P ，E ，M 三点共线时，PM -PE 的值最大，为ME 的长，求出CE ，CQ ，得到EQ ，利用垂直平分线的性质得到EM =CM =1即可．【详解】解：如图：作N 关于BD 的对称点E ，连接PE ，ME ，过点M 作MQ ⊥AC ，垂足为Q ，∴PN =PE ，则PM -PN =PM -PE ，【答案】13【分析】连接CF、AF+=+，故当EF MN EF AF类型二、翻折型最值问题例1．如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN 沿MN所在直线翻折得到△A'MN，连接A'C，则A'C长度的最小值是（）【变式训练1】如图，在矩形ABCD 中，3AB =，4=AD ，E 在AB 上，1BE =，F 是线段BC 上的动点，将EBF △沿EF 所在的直线折叠得到'EB F △，连接'B D ，则'B D 的最小值是（）A ．6B ．4C ．2D ．1-【答案】D 【详解】解：如图，'B 的运动轨迹是以E 为圆心，以BE 的长为半径的圆．所以，当'B 点落在DE 上时，'B D 取得最小值．根据折叠的性质，△EBF ≌△EB’F ，∴E 'B ⊥'B F ，∴E 'B ＝EB ，∵1BE =∴E 'B ＝1，∵3AB =，4=AD ，∴AE =3-1=2，∴DE =D 'B ＝．故选：D ．【变式训练2】如图，在正方形ABCD 中，AB =6，E 是CD 边上的中点，F 是线段BC 上的动点，将△ECF 沿EF 所在的直线折叠得到EC F '△，连接AC '，则的最小值是AC '_______．【答案】3【详解】解：∵四边形ABCD 是正方形，∴6CD AB AD ===，∵E 是CD 边上的中点，∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△，∴3EC EC '==，∴当点A ，C '，E 三点共线时，AC '最小，如图，在Rt ADE △中，由勾股定理得：AE ==3AE EC '-=-，∴AC '的最小值为3．类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥，垂足为P ，连接CM ，根据正方形的性质求出CE ，证明EDC DMP △≌△股定理求出CM ，根据CN MN CM +≥即可求出CN 【详解】解：过点M 作MP CD ⊥，垂足为P ，连接由旋转可得：DE DM =，3EF MN ==，90EDM ∠=例2．如图，长方形ABCD 中，6AB =，8BC =，E 为BC 上一点，且2BE =，F 为AB 边上的一个动点，连接EF ，将EF 绕着点E 顺时针旋转30°到EG 的位置，连接FG 和CG ，则CG 的最小值为______．【答案】2+【详解】解：如图，将线段BE 绕点E 顺时针旋转30°得到线段ET ，连接GT ，过E 作EJ CG ⊥，垂足为J ，∵四边形ABCD 是矩形，∴AB =CD =6，∠B =∠BCD =90°，∵∠BET =∠FEG =30°，∴∠BEF =∠TEG ，在△EBF 和△TEG 中，EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩，∴△EBF ≌△ETG （SAS ），∴∠B =∠ETG =90°，∴点G 的在射线TG 上运动，∴当CG ⊥TG 时，CG 的值最小，∵∠EJG =∠ETG =∠JGT =90°，∴四边形ETGJ 是矩形，∴∠JET =90°,GJ =TE =BE =2，∵∠BET =30°，∴∠JEC =180°-∠JET -∠BET =60°，∵8BC =，∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为：332.【变式训练1】如图，已知正方形ABCD 的边长为a ，点E 是AB 边上一动点，连接ED ，将ED 绕点E 顺时针旋转90︒到EF ，连接DF ，CF ，则当DF CF +之和取最小值时，DCF 的周长为______．（用含a 的代数式表示）【答案】()51a +【分析】连接BF ，过点F 作FG AB ⊥交AB 延长线于点G ，先证明AED GFE △≌△，即可得到点F 在CBG ∠的角平分线上运动，作点C 关于BF 的对称点C '，当点D ，F ，C 三点共线时，DF CF DC +='最小，根据勾股定理求出DC DF CF '=+的最小值为35，即可求出此时DCF 的周长为353+．将ED绕点E顺时针旋转90︒到EF，=，∴⊥，EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒，90∴∠=∠，ADE FEG又90，∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系，并证明你得到的结论；(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后（旋转角度大于过观察或测量等方法判断（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由；(3)若2BC DE ==，在（2）的旋转过程中，①当AE 为最大值时，则AF =___________．ABC 是等腰直角三角形，AD BC ∴⊥，BD CD =，90ADB ADC ∴∠=∠=︒．四边形DEFG 是正方形，DE DG ∴=．在BDG 和ADE V 中，BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩，(SAS)ADE BDG ∴△≌△，BG AE ∴=；（2）（1）中的结论仍然成立，BG AE =，BG AE ⊥．理由如下：如图②，连接AD ，延长EA 交BG 于K ，交DG 于O ．在Rt BAC 中，D 为斜边BC 中点，AD BD ∴=，AD BC ⊥，90ADG GDB ∴∠+∠=︒．四边形EFGD 为正方形，DE DG ∴=，且90GDE ∠=︒，90ADG ADE ∴∠+∠=︒，BDG ADE ∴∠=∠．在BDG 和ADE V 中，BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩，(SAS)BDG ADE ∴△≌△，BG AE ∴=，BGD AED ∠=∠，2，==BC DEBG∴=+=．213AE∴=．3在Rt AEF中，由勾股定理，得222=+=+3AF AE EF中，如图②中，在BDGBG∴-≤≤+，2112∴的最小值为1，此时如图④中，AE在Rt AEF中，2=AF EF【点睛】本题属于四边形综合题，考查了旋转的性质的运用，等腰直角三角形的性质的运用，勾股定理的运用，全等三角形的判定及性质的运用，正方形的性质的运用，解答时证明三角形全等是关键．类型四、PA+KPB型最值问题3A．27B．23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形，∠=∠，∴OAE OCFA．3B．22【答案】D【分析】连接AF，利用三角形中位线定理，可知四边形ABCD是菱形，∴==，AB BC23，H分别为AE，EF的中点，GGH∴是AEF△的中位线，【答案】51-【分析】连接BD交EF的中点，求出OB的长，得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点，四边形ABCD是正方形，∴==，BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线，在【详解】解：延长DC '''∴E F G H E '''、、、、在同一直线上时，四边形EFCH 作E K AB '⊥交AB 延长于点K ，则23EK BE CD A E AB CD '''=++=+=，E K BC '=+在△ABH中，∠AHB=90°，∠ABH过点D作DE∥AC交BC延长线于点E，作点C【点睛】本题考查了对称的性质，勾股定理，等边三角形的判定和性质，最值问题，直角三角形的性质，多边形的面积，知识点较多，难度较大，解题的关键是作出辅助线，得出当且仅当B，D，F三点共线时，BD+CD取得最小值．。

专题特殊四边形中的最值问题1、如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点（且点P不与点B，C重合），PE⊥AB与E，PF⊥AC于F，则EF的最小值为（）A. 4B. 4.8C. 5.2D. 62、如图，在周长为12的菱形ABCD中，AE=1，AF=2. 若P为对角线BD上一动点，则 EP+FP的最小值为（）A.1B. 2C. 3D. 43、如图，在菱形ABCD中，AB＝6，∠BAD＝60︒，点E为AB的中点，点P是对角线AC上的一个动点，则PE＋PB的最小值为（）A．3 B．6 C．33D．634、如图，正方形ABCD的周长为24，P为对角线AC上的一个动点，+的最小值为（）E是CD的中点，则PE PDA．35B．32C．6D．55、如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE＝3，点Q为对角线AC上的动点，则△BEQ周长的最小值为（）A．3 B．4 C．5 D．66、如图，在△ABC中，∠BAC=45°，AB=AC=8，P为AB边上一动点，以AP，PC为边作平行四边形PAQC，则对角线PQ的最小值为 .7、如图，折叠矩形纸片ABCD，使点B的对应点E落在CD边上，GH为折痕，已知AB=6，BC=10．当折痕GH最长时，线段BH的长为_________．【例题讲解】3.如图，菱形ABCD中，对角线AC＝6，BD＝8，M、N 分别是BC、CD上的动点，P是线段BD上的一个动点，则PM＋PN的最小值是（）A．95B．125C．165D．2455．如图，在平行四边形ABCD中，BC＝AC，E、F分别是AB、CD的中点，连接CE、AF．（1）求证：四边形AECF是矩形；（2）当平行四边形ABCD的边或角满足什么关系时，四边形AECF是正方形？请说明理由．（3）在（2）的条件下，若AE＝4，点M为EC中点，当点P在线段AC上运动时，求PE+PM的最小值．【巩固练习】1、如图，MN是正方形ABCD的一条对称轴，点P直线MN上的一个动点，当PC+PD最小时，∠PCD的度数为（）A.60°B. 90°C. 45°D. 75°2、如图，点P是矩形ABCD对角线BD上的一个动点，AB=6 ，AD=8 ，则PA+PC的最小值为.3、如图，菱形ABCD中，2AB=，120∠=︒，N是AB的中点，M是对角线B+的最小值是（）AC上的一个动点，则MN MBA．2B3C5D．44、如图，四边形ABCD是菱形，AC=8，DB=6，P，Q分别是AC，AD上的动点，连接DP，PQ，则DP+PQ的最小值为.5、如图所示，菱形ABCD中，∠B=60°，AB=2，点E，F分别是AB，AD上的动点，且满足BE=AF，连结EF，EC，CF.（1）求证△EFC是等边三角形.试探究△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．。

专题18.8 四边形中的最值问题专项训练（30道）【人教版】考卷信息：本套训练卷共30题，选择10题，填空10题，解答10题，题型针对性较高，覆盖面广，选题有深度，可强化学生对四边形中最值问题模型的记忆与理解！一．选择题（共10小题）1．（2022春•重庆期末）如图，矩形ABCD中，AB＝23，BC＝6，P为矩形内一点，连接PA，PB，PC，则PA+PB+PC的最小值是（ ）A．43+3B．221C．23+6D．45【分析】将△BPC绕点C逆时针旋转60°，得到△EFC，连接PF、AE、AC，则AE的长即为所求．【解答】解：将△BPC绕点C逆时针旋转60°，得到△EFC，连接PF、AE、AC，则AE 的长即为所求．由旋转的性质可知：△PFC是等边三角形，∴PC＝PF，∵PB＝EF，∴PA+PB+PC＝PA+PF+EF，∴当A、P、F、E共线时，PA+PB+PC的值最小，∵四边形ABCD是矩形，∴∠ABC＝90°，∴AC=AB2+BC2=43，∴AC＝2AB，∴∠ACB＝30°，AC＝2AB＝43，∵∠BCE＝60°，∴∠ACE＝90°，∴AE=(43)2+62=221，故选：B．2．（2022•灞桥区校级模拟）如图，平面内三点A、B、C，AB＝4，AC＝3，以BC为对角线作正方形BDCE，连接AD，则AD的最大值是（ ）2 A．5B．7C．72D．72【分析】如图将△BDA绕点D顺时针旋转90°得到△CDM．由旋转不变性可知：AB＝AM，CM＝4，DA＝DM．∠ADM＝90°，推出△ADM是等腰直角三角形，推出AD=22推出当AM的值最大时，AD的值最大，利用三角形的三边关系求出AM的最大值即可解决问题；【解答】解：如图将△BDA绕点D顺时针旋转90°得到△CDM．由旋转不变性可知：AB＝CM＝4，DA＝DM．∠ADM＝90°，∴△ADM是等腰直角三角形，AM，∴AD=22∴当AM的值最大时，AD的值最大，∵AM≤AC+CM，∴AM≤7，∴AM的最大值为7，，∴AD的最大值为722故选：D ．3．（2022春•中山市期末）如图，在边长为a 的正方形ABCD 中，E 是对角线BD 上一点，且BE ＝BC ，点P 是CE 上一动点，则点P 到边BD ，BC 的距离之和PM +PN 的值（ ）A ．有最大值aB ．有最小值22a C ．是定值a D ．是定值22a 【分析】连接BP ，作EF ⊥BC 于点F ，由正方形的性质可知△BEF 为等腰直角三角形，BE ＝a ，可求EF ，利用面积法得S △BPE +S △BPC ＝S △BEC ，将面积公式代入即可．【解答】解：如图，连接BP ，作EF ⊥BC 于点F ，则∠EFB ＝90°，∵正方形的性质可知∠EBF ＝45°，∴△BEF 为等腰直角三角形，∵正方形的边长为a ，∴BE ＝BC ＝a ，∴BF ＝EF =22BE =22a ，∵PM ⊥BD ，PN ⊥BC ，∴S △BPE +S △BPC ＝S △BEC ，∴12BE ×PM +12BC ×PN =12BC ×EF ，∵BE ＝BC ，∴PM +PN ＝EF =22a ．则点P 到边BD ，BC 的距离之和PM +PN 的值是定值22a ．故选：D ．4．（2022春•三门峡期末）如图，在矩形ABCD 中，AB ＝2，AD ＝1，E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是（ ）A．2B．4C．2D．22【分析】根据中位线定理可得出点点P的运动轨迹是线段P1P2，再根据垂线段最短可得当BP⊥P1P2时，PB取得最小值；由矩形的性质以及已知的数据即可知BP1⊥P1P2，故BP 的最小值为BP1的长，由勾股定理求解即可．【解答】解：如图：当点F与点C重合时，点P在P1处，CP1＝DP1，当点F与点E重合时，点P在P2处，EP2＝DP2，CE．∴P1P2∥CE且P1P2=12当点F在EC上除点C、E的位置处时，有DP＝FP．CF．由中位线定理可知：P1P∥CE且P1P=12∴点P的运动轨迹是线段P1P2，∴当BP⊥P1P2时，PB取得最小值．∵矩形ABCD中，AB＝2，AD＝1，E为AB的中点，∴△CBE、△ADE、△BCP1为等腰直角三角形，CP1＝1．∴∠ADE＝∠CDE＝∠CP1B＝45°，∠DEC＝90°．∴∠DP2P1＝90°．∴∠DP1P2＝45°．∴∠P2P1B＝90°，即BP1⊥P1P2，∴BP的最小值为BP1的长．在等腰直角BCP1中，CP1＝BC＝1．∴BP1=2．∴PB的最小值是2．故选：C．5．（2022春•滨湖区期末）如图，已知菱形ABCD的面积为20，边长为5，点P、Q分别是边BC、CD上的动点，且PC＝CQ，连接PD、AQ，则PD+AQ的最小值为（ ）A．45B．89C．10D．72【分析】过点A作AM⊥BC于点M，延长AM到点A′，使A′M＝AM，根据菱形的性质和勾股定理可得BM＝3，以点B为原点，BC为x轴，垂直于BC方向为y轴，建立平面直角坐标系，可得B（0，0），A（3，4），C（5，0），D（8，4），A′（3，﹣4），然后证明△ABP≌△ADQ（SAS），可得AP＝AQ＝A′P，连接A′D，AP，A′P，由A′P+PD＞A′D，可得A′，P，D三点共线时，PD+A′P取最小值，所以PD+AQ 的最小值＝PD+A′P的最小值＝A′D，利用勾股定理即可解决问题．【解答】解：如图，过点A作AM⊥BC于点M，延长AM到点A′，使A′M＝AM，∵四边形ABCD是菱形，∴AB＝BC＝AD＝5，∠ABC＝∠ADC，∵菱形ABCD的面积为20，边长为5，∴AM＝4，在Rt△ABM中，根据勾股定理得：BM=AB2−AM2=3，以点B为原点，BC为x轴，垂直于BC方向为y轴，建立平面直角坐标系，∴B（0，0），A（3，4），C（5，0），D（8，4），A′（3，﹣4），∵PC＝CQ，BC＝CD，∴BP＝DQ，在△ABP和△ADQ中，AB=AD∠ABC=∠ADC，BP=DQ∴△ABP≌△ADQ（SAS），∴AP＝AQ＝A′P，连接A′D，AP，A′P，∵A′P+PD＞A′D，∴A′，P，D三点共线时，PD+A′P取最小值，∴PD+AQ的最小值＝PD+A′P的最小值＝A′D=(8−3)2+(4+4)2=89．故选：B．6．（2022•泰山区一模）如图，M、N是正方形ABCD的边CD上的两个动点，满足AM＝BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为2，则线段CF的最小值是（ ）A．2B．1C．5−1D．5−2【分析】根据正方形的性质可得AD＝BC＝CD，∠ADC＝∠BCD，∠DCE＝∠BCE，然后利用“HL”证明Rt△ADM和Rt△BCN全等，根据全等三角形对应角相等可得∠1＝∠2，利用“SAS”证明△DCE和△BCE全等，根据全等三角形对应角相等可得∠2＝∠3，从而得到∠1＝∠3，然后求出∠AFD＝90°，取AD的中点O，连接OF、OC，根据直角AD＝1，利用勾股定理列式求出OC，然三角形斜边上的中线等于斜边的一半可得OF=12后根据三角形的三边关系可知当O、F、C三点共线时，CF的长度最小．【解答】解：在正方形ABCD中，AD＝BC＝CD，∠ADC＝∠BCD，∠DCE＝∠BCE，在Rt△ADM和Rt△BCN中，AD=BCAM=BN，∴Rt△ADM≌Rt△BCN（HL），∴∠1＝∠2，在△DCE和△BCE中，BC=CD∠DCE=∠BCE，CE=CE∴△DCE≌△BCE（SAS），∴∠2＝∠3，∴∠1＝∠3，∵∠ADF+∠3＝∠ADC＝90°，∴∠1+∠ADF＝90°，∴∠AFD＝180°﹣90°＝90°，取AD的中点O，连接OF、OC，AD＝1，则OF＝DO=12在Rt△ODC中，OC=DO2+DC2=12+22=5，根据三角形的三边关系，OF+CF＞OC，∴当O、F、C三点共线时，CF的长度最小，最小值＝OC﹣OF=5−1．故选：C．7．（2022•龙华区二模）如图，已知四边形ABCD是边长为4的正方形，E为CD上一点，且DE＝1，F为射线BC上一动点，过点E作EG⊥AF于点P，交直线AB于点G．则下列结论中：①AF＝EG；②若∠BAF＝∠PCF，则PC＝PE；③当∠CPF＝45°时，BF＝1；④PC的最小值为13−2．其中正确的有（ ）A．1个B．2个C．3个D．4个【分析】连接AE，过E作EH⊥AB于H，则EH＝BC，根据全等三角形的判定和性质定理即可得到AF＝EG，故①正确；根据平行线的性质和等腰三角形的判定和性质即可得到PE＝PC；故②正确；连接EF，推出点E、P、F、C四点共圆，根据圆周角定理得到∠FEC＝∠FPC＝45°，于是得到BF＝DE＝1，同理当F运动到C点右侧时，此时∠FPC＝45°，且EPCF四点共圆，EC＝FC＝3，故此时BF＝BC+CF＝4+3＝7．因此BF＝1或7，故③错误；取AE的中点O，连接PO，CO，根据直角三角形的性质得到AO＝PO =1AE，推出点P在以O为圆心，AE为直径的圆上，当OC最小时，CP的值最小，根2据三角形的三边关系得到PC≥OC﹣OP，根据勾股定理即可得到结论．【解答】解：连接AE，过E作EH⊥AB于H，则EH＝BC，∵AB＝BC，∴EH＝AB，∵EG⊥AF，∴∠BAF+∠AGP＝∠BAF+∠AFB＝90°，∴∠EGH＝∠AFB，∵∠B＝∠EHG＝90°，∴△HEG≌△ABF（AAS），∴AF＝EG，故①正确；∵AB∥CD，∴∠AGE＝∠CEG，∵∠BAF+∠AGP＝90°，∠PCF+∠PCE＝90°，∵∠BAF＝∠PCF，∴∠AGE＝∠PCE，∴∠PEC＝∠PCE，∴PE＝PC；故②正确；连接EF，∵∠EPF＝∠FCE＝90°，∴点E、P、F、C四点共圆，∴∠FEC＝∠FPC＝45°，∴EC＝FC，∴BF＝DE＝1，同理当F运动到C点右侧时，此时∠FPC＝45°，且E、P、C、F四点共圆，EC＝FC＝3，故此时BF＝BC+CF＝4+3＝7．因此BF＝1或7，故③错误；取AE的中点O，连接PO，CO，AE，∴AO＝PO=12∵∠APE＝90°，∴点P在以O为圆心，AE为直径的圆上，∴当OC最小时，CP的值最小，∵PC ≥OC ﹣OP ，∴PC 的最小值＝OC ﹣OP ＝OC −12AE ，∵OC =22+(72)2=652，在Rt △ADE 中，AE =42+12=17，∴PC 的最小值为652−172，故④错误，故选：B ．8．（2022•南平校级自主招生）如图，在△ABC 中，AB ＝6，AC ＝8，BC ＝10，P 为边BC 上一动点（且点P 不与点B 、C 重合），PE ⊥AB 于E ，PF ⊥AC 于F ．则EF 的最小值为（ ）A ．4B ．4.8C ．5.2D ．6【分析】先由矩形的判定定理推知四边形PEAF 是矩形；连接PA ，则PA ＝EF ，所以要使EF ，即PA 最短，只需PA ⊥CB 即可；然后根据三角形的等积转换即可求得PA 的值．【解答】解：如图，连接PA ．∵在△ABC 中，AB ＝6，AC ＝8，BC ＝10，∴BC 2＝AB 2+AC 2，∴∠A ＝90°．又∵PE ⊥AB 于点E ，PF ⊥AC 于点F ．∴∠AEP ＝∠AFP ＝90°，∴四边形PEAF 是矩形．∴AP ＝EF ．∴当PA 最小时，EF 也最小，即当AP ⊥CB 时，PA 最小，∵12AB •AC =12BC •AP ，即AP =AB ⋅AC BC =6×810=4.8，∴线段EF 长的最小值为4.8；故选：B ．9．（2022春•崇川区期末）如图，正方形ABCD 边长为1，点E ，F 分别是边BC ，CD 上的两个动点，且BE ＝CF ，连接BF ，DE ，则BF +DE 的最小值为（ ）A ．2B ．3C ．5D ．6【分析】连接AE ，利用△ABE ≌△BCF 转化线段BF 得到BF +DE ＝AE +DE ，则通过作A 点关于BC 对称点H ，连接DH 交BC 于E 点，利用勾股定理求出DH 长即可．【解答】解：连接AE ，如图1，∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABE ＝∠BCF ＝90°．又BE ＝CF ，∴△ABE ≌△BCF （SAS ）．∴AE ＝BF ．所以BF +DE 最小值等于AE +DE 最小值．作点A 关于BC 的对称点H 点，如图2，连接BH ，则A 、B 、H 三点共线，连接DH ，DH 与BC 的交点即为所求的E 点．根据对称性可知AE ＝HE ，所以AE +DE ＝DH ．在Rt △ADH 中，AD ＝1，AH ＝2，∴DH =AH 2+AD 2=5，∴BF +DE 最小值为5．故选：C ．10．（2022•泰州）如图，正方形ABCD的边长为2，E为与点D不重合的动点，以DE为一边作正方形DEFG．设DE＝d1，点F、G与点C的距离分别为d2、d3，则d1+d2+d3的最小值为（ ）A．2B．2C．22D．4【分析】连接AE，那么，AE＝CG，所以这三个d的和就是AE+EF+FC，所以大于等于AC，故当AEFC四点共线有最小值，最后求解，即可求出答案．【解答】解：如图，连接AE，∵四边形DEFG是正方形，∴∠EDG＝90°，EF＝DE＝DG，∵四边形ABCD是正方形，∴AD＝CD，∠ADC＝90°，∴∠ADE＝∠CDG，∴△ADE≌△CDG（SAS），∴AE＝CG，∴d1+d2+d3＝EF+CF+AE，∴点A，E，F，C在同一条线上时，EF+CF+AE最小，即d1+d2+d3最小，连接AC，∴d1+d2+d3最小值为AC，在Rt△ABC中，AC=2AB＝22，∴d1+d2+d3最小＝AC＝22，故选：C．二．填空题（共10小题）11．（2022春•江城区期末）如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB＝6，BC＝2．运动过程中点D到点O的最大距离是　3+13　．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于的一半可得OE=12第三边可得OD过点E时最大．【解答】解：如图：取线段AB的中点E，连接OE，DE，OD，∵AB＝6，点E是AB的中点，∠AOB＝90°，∴AE＝BE＝3＝OE，∵四边形ABCD是矩形，∴AD＝BC＝2，∠DAB＝90°，∴DE=AE2+AD2=13，∵OD≤OE+DE，∴当点D，点E，点O共线时，OD的长度最大．∴点D到点O的最大距离＝OE+DE＝3+13，故答案为：3+13．12．（2022•东莞市校级一模）如图，在矩形ABCD中，AB＝6，AD＝5，点P在AD上，点Q在BC上，且AP＝CQ，连接CP，QD，则PC+DQ的最小值为　13　．【分析】连接BP，在BA的延长线上截取AE＝AB＝6，连接PE，CE，PC+QD＝PC+PB，则PC+QD的最小值转化为PC+PB的最小值，在BA的延长线上截取AE＝AB＝6，则PC+QD＝PC+PB＝PC+PE≥CE，根据勾股定理可得结果．【解答】解：如图，连接BP，∵四边形ABCD是矩形，∴AD∥BC，AD＝BC，∵AP＝CQ，∴AD﹣AP＝BC﹣CQ，∴DP＝QB，DP∥BQ，∴四边形DPBQ是平行四边形，∴PB∥DQ，PB＝DQ，∴PC+QD＝PC+PB，∴PC+QD的最小值转化为PC+PB的最小值，如图，在BA的延长线上截取AE＝AB＝6，连接PE，CE，∵PA⊥BE，∴PA是BE的垂直平分线，∴PB＝PE，∴PC+PB＝PC+PE，∴PC+QD＝PC+PB＝PC+PE≥CE，∵BE＝2AB＝12，BC＝AD＝5，∴CE=BE2+BC2=13．∴PC+DQ的最小值为13．故答案为：13．13．（2022•钱塘区一模）如图，在矩形ABCD中，线段EF在AB边上，以EF为边在矩形ABCD内部作正方形EFGH，连结AH，CG．若AB＝10，AD＝6，EF＝4，则AH+CG的最小值为　62　．【分析】方法一：延长DA至A′，使A′A＝EH＝EF＝4，连接A′E，EG，可得四边形AA′EH是平行四边形，所以A′E＝AH，则AH+CG的最小值即为A′E+CG的最小值，根据勾股定理即可解决问题．方法二：过点G作GA′∥AH交AF于点A′，可得四边形AHGA′是平行四边形，进而可以解决问题．【解答】解：方法一：如图，延长DA至A′，使A′A＝EH＝EF＝4，连接A′E，EG，∵HE⊥AB，AA′⊥AB，∴AA′∥EH，∵A′A＝EH，∴四边形AA′EH是平行四边形，∴A′E＝AH，则AH+CG的最小值即为A′E+CG的最小值，∵四边形EFGH是正方形，∴EF＝FG＝4，∴EG＝42，∵A′D＝AD+AA′＝6+4＝10，在Rt△A′DC中，DC＝AB＝10，∴A′C=A′D2+DC2=102，∴A′E+CG＝A′C﹣EG＝62．方法二：如图，过点G作GA′∥AH交AF于点A′，∴四边形AHGA′是平行四边形，∴AA′＝HG＝4，A′G＝AH，∴A′B＝AB﹣AA′＝6，∵BC＝6，∴A′C＝62，∴AH+CG＝A′G+CG≥A′C，则AH+CG的最小值为62．故答案为：62．14．（2022春•东城区期中）在正方形ABCD中，AB＝5，点E、F分别为AD、AB上一点，且AE＝AF，连接BE、CF，则BE+CF的最小值是　55　．【分析】连接DF，根据正方形的性质证明△ADF≌△ABE（SAS），可得DF＝BE，作点D关于AB的对称点D′，连接CD′交AB于点F′，连接D′F，则DF＝D′F，可得BE+CF＝DF+CF＝D′F+CF≥CD′，所以当点F与点F′重合时，D′F+CF最小，最小值为CD′的长，然后根据勾股定理即可解决问题．【解答】解：如图，连接DF，∵四边形ABCD是正方形，∴AD＝AB，∠BAE＝∠DAF＝90°，在△ADF 和△ABE 中，AD =AB ∠FAD =∠EAB AF =AE，∴△ADF ≌△ABE （SAS ），∴DF ＝BE ，作点D 关于AB 的对称点D ′，连接CD ′交AB 于点F ′，连接D ′F ，则DF ＝D ′F ，∴BE +CF ＝DF +CF ＝D ′F +CF ≥CD ′，∴当点F 与点F ′重合时，D ′F +CF 最小，最小值为CD ′的长，在Rt △CDD ′中，根据勾股定理得：CD ′=CD 2+DD′2=52+102=55，∴BE +CF 的最小值是55．故答案为：55．15．（2022春•虎林市期末）如图，在Rt △ABC 中，∠BAC ＝90°，且BA ＝12，AC ＝16，点D 是斜边BC 上的一个动点，过点D 分别作DE ⊥AB 于点E ，DF ⊥AC 于点F ，点G 为四边形DEAF 对角线交点，则线段GF 的最小值为 245　．【分析】由勾股定理求出BC 的长，再证明四边形DEAF 是矩形，可得EF ＝AD ，根据垂线段最短和三角形面积即可解决问题．【解答】解：连接AD 、EF ，∵∠BAC ＝90°，且BA ＝9，AC ＝12，∴BC =AB 2+AC 2=122+162=20，∵DE ⊥AB ，DF ⊥AC ，∴∠DEA ＝∠DFA ＝∠BAC ＝90°，∴四边形DEAF 是矩形，∴EF ＝AD ，∴当AD ⊥BC 时，AD 的值最小，此时，△ABC 的面积=12AB ×AC =12BC ×AD ，∴12×16＝20AD ，∴AD =485∴EF 的最小值为485，∵点G 为四边形DEAF 对角线交点，∴GF =12EF =245；故答案为：245．。

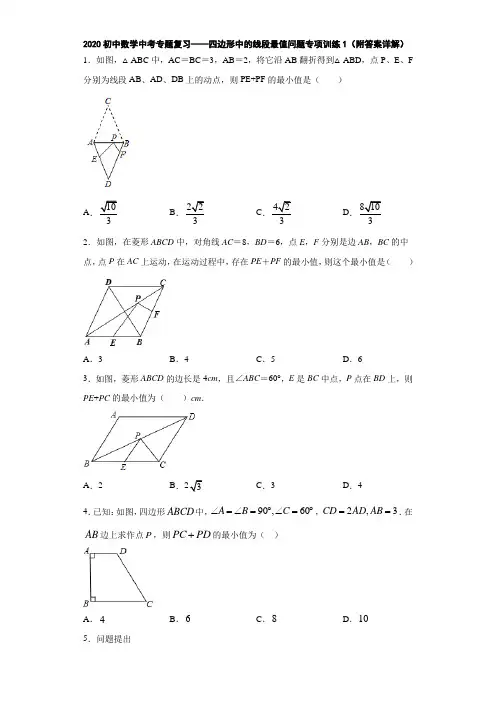
期末复习专题四边形中最值问题一、选择题如图，在平行四边形ABCD中，∠A=45∘，AD=4，点M，N分别是边AB，BC上的动点，连接DN，MN，点E，F分别为DN，MN的中点，连接EF，则EF的最小值为( )A．1B．√2C．√22D．2√2如图，在Rt△ABC中，∠B=90∘，AB=6，BC=8，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE的最小值是( )A．4B．6C．8D．10如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为( )A．54B．52C．53D．65如图四边形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3，P为AB边上的一动点，以PD，PC为边作平行四边形PCQD，则对角线PQ的长的最小值是( )A．3B．4C．5D．6如图，矩形ABCD中，AB=8，BC=4，把矩形ABCD沿过点A的直线AE折叠，点D落在矩形ABCD内部的点Dʹ处，则CDʹ的最小值是( )A．4B．4√5C．4√5−4D．4√5+4如图，菱形ABCD的边长为4，∠A=60∘，E是边AD的中点，F是边AB上的一个动点，将线段EF绕着点E逆时针旋转60∘得到EG，连接BG，CG，则BG+CG的最小值为( )A．3√3B．2√7C．4√3D．2+2√3如图，在矩形ABCD中，AB=6，AD=8，以BC为斜边在矩形的外部作直角三角形BEC，点F是CD的中点，则EF最大值为( )A．8B．9C．10D．2√41如图，在平行四边形ABCD中，∠C=120∘，AD=4，AB=2，点E是折线BC−CD−DA上的一个动点（不与A，B重合）．则△ABE的面积的最大值是( )B．1C．3√2D．2√3A．√32二、填空题如图，长方形ABCD中AB=2，BC=4，正方形AEFG的边长为1．正方形AEFG绕点A旋转的过程中，线段CF的长的最小值为．如图，已知平行四边形ABCO的顶点A，C分别在直线x=2和x=7上，O是坐标原点，则对角线OB长的最小值为．如图，已知矩形ABCD的边AB=3，AD=8，顶点A，D分别在x轴，y轴上滑动，在矩形滑动过程中，点C到原点O距离的最大值是．如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P，Q分别是AD和AE上的动点，则DQ+PQ的最小值是．如图，在平面直角坐标系中有菱形OABC，C点坐标为(1,2)，点P是对角线OB上一动点，E点坐标为(0,−1)，则EP+AP最小值为．如图，平行四边形ABCO的边OC在直角坐标系的x轴上，AB交y轴于点D，AD=4，OC=10，∠A=60∘，线段EF垂直平分OD，点P为线段EF上的动点，PM⊥x轴于点M，点E与Eʹ关于x轴对称．则BP+PM+MEʹ的长度的最小值．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线BD 上有一点P，使PC+PE的和最小，则这个最小值为．如图，菱形ABCD中，AB=2，∠BAD=60∘，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是．如图，在矩形ABCD中，AB=4，AD=3，矩形内部有一动点P满足S△PAB=13S矩形ABCD，则点P到A，B两点的距离之和PA+PB的最小值为．如图，在矩形ABCD中，AB=4，AD=5，连接AC，O是AC的中点，M是AD上一点，且MD=1，P是BC上一动点，则PM−PO的最大值为．三、解答题如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上的一动点，求DN+MN的最小值．如图，在菱形ABCD中，AB=4，∠BAD=120∘，△AEF为正三角形，点E，F分别在菱形的边BC，CD上滑动，且E，F不与B，C，D重合．当点EF在BC，CD上滑动时，求△CEF面积的最大值．如图，在矩形ABCD中，AB=4，AD=2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，求PB的最小值．如图，在边长为1的菱形ABCD中，∠ABC=60∘，将△ABD沿射线BD的方向平移得到△AʹBʹDʹ，分别连接AʹC，AʹD，BʹC，求AʹC+BʹC的最小值．。

特殊的平行四边形中的最值模型--胡不归模型胡不归模型可看作将军饮马衍生，主要考查转化与化归等的数学思想，近年在中考数学和各地的模拟考中常以压轴题的形式考查，学生不易把握。

本专题就最值模型中的胡不归问题进行梳理及对应试题分析，方便掌握。

在解决胡不归问题主要依据是：点到线的距离垂线段最短。

【模型背景】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据“两点之间线段最短”，虽然从他此刻位置A 到家B 之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？”看到这里很多人都会有一个疑问，少年究竟能不能提前到家呢？假设可以提早到家，那么他该选择怎样的一条路线呢？这就是今天要讲的“胡不归”问题.补充知识：在直角三角形中锐角A 的对边与斜边的比叫做∠A 的正弦，记作sin A ，即sin A =∠A 的对边斜边。

若无法理解正弦，也可考虑特殊直角三角形(含30°，45°，60°)的三边关系。

【模型解读】一动点P 在直线MN 外的运动速度为V 1，在直线MN 上运动的速度为V 2，且V 1<V 2，A 、B 为定点，点C 在直线MN 上，确定点C 的位置使AC V 2+BC V 1的值最小．(注意与阿氏圆模型的区分)1)AC V 2+BC V 1=1V 1BC +V 1V 2AC，记k =V 1V 2，即求BC +kAC 的最小值.2)构造射线AD 使得sin ∠DAN =k ，CH AC=k ，CH =kAC ,将问题转化为求BC +CH 最小值.3)过B 点作BH ⊥AD 交MN 于点C ，交AD 于H 点，此时BC +CH 取到最小值，即BC +kAC 最小．【解题关键】在求形如“PA +kPB ”的式子的最值问题中，关键是构造与kPB 相等的线段，将“PA +kPB ”型问题转化为“PA +PC ”型．(若k >1，则提取系数，转化为小于1的形式解决即可)。

专题04特殊平行四边形中全等相似与最值问题通用的解题思路:一、四边形与全等相似1.三角形与全等之六大全等模型:(1)一线三等角模型锐角一线三等角(2)手拉手模型(3)半角模型(4)倍长中线模型模型(6)雨伞等模型(5)平行线中等模型2.三角形与相似之四大相似模型:(1)A字模型(3)手拉手模型(2)8字模型(4)一线三等角模型B 二、四边形线段最值问题囹 1 C B D 02B （1）将军饮马模型两定一动模型一定两动模型两线段相减的最大值模型（三点共线）• B（2）费马点模型：将边以A 为顶点逆时针旋转60。

，得到AQE,连接P0则^APQ 为等边三角形,PA=PQ O1. （2023-r 东深圳•中考真题）（1）如图，在矩形ABCD 中，E 为AD 边上一点，连接BE,①若= 过C 作CFLBE 交BE 于点、F ,求证：AABE^AFCB ；②若S 矩形倔8 = 2。

时，则BECF=(2)如图，在菱形ABCD 中，cosA = |,过。

作CE1AB 交A8的延长线于点E,过E 作EF _LAD 交AD 于点、F ,若S 菱形*d =24时，求EF BC 的值.(3)如图，在平行四边形ABCD 中，匕4 = 60。

，AB = 6, AD=5,点E 在CD 上，且CE = 2,点F 为BC 上一点，连接时，过E 作EGLEF 交平行四边形ABCD 的边于点G,若EF ・EG = 70时，请直接写出AG 的长.D,E E a C C A B AB备用图2.（2022广东广州•中考真题）如图，在菱形ABCQ中，0BAD=120°,AB=6,连接8Q.⑴求BQ的长；⑵点E为线段BQ上一动点（不与点B,。

重合），点E在边AQ上，且BE二也DF,①当CE±AB时，求四边形的面积；②当四边形的面积取得最小值时，CE+右CT的值是否也最小？如果是，求CE+也CF的最小值；如果不是，请说明理由.题型一特殊平行四边形中全等相似计算1.（2024-P东汕头•一模）（1）如图1,在矩形ABCD中，E为AD边上一点，连接8E,①若BE=BC,过。

2022-2023学年初二数学第二学期培优专题06 平行四边形中的最值问题【例题讲解】如图，在平行四边形ABCD 中，30BCD ∠=︒，6BC =，33CD =，（1）平行四边形ABCD 的面积为________．（2）若M 是AD 边的中点，N 是AB 边上的一个动点，将AMN 沿MN 所在直线翻折得到A MN '△，连接A C '，则A C '长度的最小值是________．解：（1）过点C 作CF ⊥AB ，交AB 延长线于F ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，BC =6，AB =CD =33，∵∠BCD =30°=∠CBF ，∴CF =12BC =3， ∴四边形ABCD 的面积=AB CF ⨯=333⨯=93；（2）连接MC ，过点M 作ME ⊥CD 于E ，交CD 的延长线于点E ；∵四边形ABCD 为平行四边形，∴AD ∥BC ，AD =BC =6，∵点M 为AD 的中点，∠BCD =30°，∴DM =MA =3，∠MDE =∠BCD =30°，∴ME =12DM =32，DE =332，∴CE =CD +DE =33332+=932，由勾股定理得：CM 2=ME 2+CE 2， ∴CM=2239322⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭=37，由翻折变换的性质得：MA ′=MA =3，∵MA ′+A ′C ≥MC ， ∴A ′C ≥MC- MA ′= MC -3，显然，当折线MA ′C 与线段MC 重合时，线段A ′C 的长度最短，此时A ′C =373-，故答案为：（1）93；（2）373-．【综合演练】1．如图 ，在平行四边形ABCD 中 ，120C ∠=︒ ，AB =4 ，AD =8 ， 点H 、G 分别是边CD 、BC 上的动点．连接AH 、HG ，点E 为AH 的中点 ，点F 为GH 的中点 ，连接EF ．则EF 的最大值与最小值的差为（ ）A ．2B ．232-C ．3D ．43-2．如图，在△ABC 中，∠ACB ＝60°，∠CAB ＝45°，BC ＝4，点D 为AB 边上一个动点，连接CD ，以DA 、DC 为一组邻边作平行四边形ADCE ，则对角线DE 的最小值是（ ）A ．2+6B ．1+3C ．4D ．2+23第II 卷（非选择题）二、填空题(共0分)3．如图，在Rt ABC 中，90,3,4B AB BC ∠=︒==，点D 为BC 上一动点（不与点C 重合），以AD ，CD 为一组邻边作平行四边形ADCE ，当DE 的值最小时，平行四边形ADCE 的周长．．为_____． 4．如图，在ABCD 中，=60B ∠︒，10AB =，8BC =，点E 为边AB 上的一个动点，连接ED ，EC ， 以ED 、CE 为邻边构造EDGC ，连接EG ，则EG 的最小值为__________．5．如图，平行四边形ABCD 中，AB ＝2，AD ＝1，∠ADC ＝60°，将平行四边形ABCD 沿过点A 的直线l 折叠，使点D 落到AB 边上的点D 处，折痕交CD 边于点E ．若点P 是直线l 上的一个动点，则PD '+PB 的最小值_______．6．如图，平行四边形ABCD中，8∠=︒，E是边AD上且2AAB=，6AD=，60=，F是边AB上AE DE+的最小值__________．的一个动点，将线段EF绕点E逆时针旋转60︒，得到EG，连接BG、CG，则BG CG7．如图，CD是直线x＝1上长度固定为1的一条动线段．已知A（﹣1，0），B（0，4），则四边形ABCD 周长的最小值为_________________．8．如图四边形ABCD，AD∥BC，AB⊥BC，AD＝1，AB＝2，BC＝3，P为AB边上的一动点，以PD，PC 为边作平行四边形PCQD，则对角线PQ的长的最小值是_____．9．如图，四边形ABCD中，∠B＝∠D＝90°，∠C＝50°，在BC、CD边上分别找到点M、N，当△AMN 周长最小时，∠AMN＋∠ANM的度数为______．10．如图，在ABCD 中，对角线AC 、BD 相交于点O ，点E 、F 分别是边AD 、AB 上的点，连结OE 、OF 、EF ．若7AB =，52BC =，45DAB ∠=︒，则OEF 周长的最小值是_______．11．如图，点(1,3),(6,1),(,0),(2,0)A B P a N a --+为四边形的四个顶点，当四边形PABN 的周长最小时，=a ________．12．如图，在四边形ABCD 中，90,5,4,A D AB AD ∠=∠=︒==3,CD =点P 是边AD 上的动点，则PBC 周长的最小值为（ ）A ．8B ．45C ．12D ．65三、解答题(共0分)13．如图，四边形ABCD 为平行四边形，延长AD 到点E ，使DE AD =，且BE DC ⊥．(1)求证：四边形DBCE 为菱形；(2)若DBC △是边长为2的等边三角形，点P 、M 、N 分别在线段BE 、BC 、CE 上运动，求PM PN +的最小值．14．如图，在平行四边形ABCD 中，2,1,60AB AD B ==∠=︒，将平行四边形ABCD 沿过点A 的直线l 折叠，使点D 落到AB 边上的点'D 处，折痕交CD 边于点E ．（1）求证：四边形'BCED 是菱形；（2）若点P 是直线l 上的一个动点，请作出使'PD PB +为最小值的点P ，并计算'PD PB +．15．如图，在平行四边形ABCD 中，30BCD ∠=︒，6BC =，33CD =，（1）平行四边形ABCD 的面积为________．（2）若M 是AD 边的中点，N 是AB 边上的一个动点，将AMN 沿MN 所在直线翻折得到A MN '△，连接A C '，则A C '长度的最小值是________．答案与解析【例题讲解】如图，在平行四边形ABCD 中，30BCD ∠=︒，6BC =，33CD =，（1）平行四边形ABCD 的面积为________．（2）若M 是AD 边的中点，N 是AB 边上的一个动点，将AMN 沿MN 所在直线翻折得到A MN '△，连接A C '，则A C '长度的最小值是________．解：（1）过点C 作CF ⊥AB ，交AB 延长线于F ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，BC =6，AB =CD =33，∵∠BCD =30°=∠CBF ，∴CF =12BC =3， ∴四边形ABCD 的面积=AB CF ⨯=333⨯=93；（2）连接MC ，过点M 作ME ⊥CD 于E ，交CD 的延长线于点E ；∵四边形ABCD 为平行四边形，∴AD ∥BC ，AD =BC =6，∵点M 为AD 的中点，∠BCD =30°，∴DM =MA =3，∠MDE =∠BCD =30°，∴ME =12DM =32，DE =332，∴CE =CD +DE =33332+=932，由勾股定理得：CM 2=ME 2+CE 2， ∴CM=2239322⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭=37，由翻折变换的性质得：MA ′=MA =3，∵MA ′+A ′C ≥MC ， ∴A ′C ≥MC- MA ′= MC -3，显然，当折线MA ′C 与线段MC 重合时，线段A ′C 的长度最短，此时A ′C =373-，故答案为：（1）93；（2）373-．【综合演练】1．如图 ，在平行四边形ABCD 中 ，120C ∠=︒ ，AB =4 ，AD =8 ， 点H 、G 分别是边CD 、BC 上的动点．连接AH 、HG ，点E 为AH 的中点 ，点F 为GH 的中点 ，连接EF ．则EF 的最大值与最小值的差为（ ） A ．2 B ．232- C ．3 D ．43- 【答案】C【分析】如图，取AD 的中点M ，连接CM 、AG 、AC ，作AN ⊥BC 于N ．首先证明∠ACD ＝90°，求出AC ，AN ，利用三角形中位线定理，可知EF ＝12AG ，求出AG 的最大值以及最小值即可解决问题． 【解答】解：如图，取AD 的中点M ，连接CM 、AG 、AC ，作AN ⊥BC 于N ．∵四边形ABCD 是平行四边形，∠BCD ＝120°，28AD AB ==∴∠D ＝180°−∠BCD ＝60°，AB ＝CD ＝4，∵AM ＝DM ＝DC ＝4，∴△CDM 是等边三角形，∴∠DMC ＝∠MCD ＝60°，AM ＝MC ，∴∠MAC ＝∠MCA ＝30°，∴∠ACD ＝90°，∴AC ＝43在Rt △ACN 中，∵AC ＝43，∠ACN ＝∠DAC ＝30°，∴AN ＝12AC ＝23∵AE ＝EH ，GF ＝FH ，∴EF ＝12AG ，∵点G 在BC 上，∴AG 的最大值为AC 的长，最小值为AN 的长，∴AG 的最大值为43，最小值为23，∴EF 的最大值为23，最小值为3，∴EF的最大值与最小值的差为：3故选C．【点评】本题考查平行四边形的性质、三角形的中位线定理、等边三角形的判定和性质、直角三角形30度角性质、垂线段最短等知识，解题的关键是学会添加常用辅助线，本题的突破点是证明∠ACD＝90°，属于中考选择题中的压轴题．2．如图，在△ABC中，∠ACB＝60°，∠CAB＝45°，BC＝4，点D为AB边上一个动点，连接CD，以DA、DC为一组邻边作平行四边形ADCE，则对角线DE的最小值是（）A．2+6B．1+3C．4 D．2+23【答案】ABC＝2，AF＝BF＝3CF 【分析】设DE交AC于O，作BF⊥AC于F，由直角三角形的性质得出CF＝12AC＝1+3，DO＝EO，当OD⊥AB ＝23，求出AC＝CF+AF＝2+23，由平行四边形性质得出AO＝CO＝12时，DO的值最小，即DE的值最小，则△AOD是等腰直角三角形，即可得出结果．【解答】解：设DE交AC于O，作BF⊥AC于F，如图所示：则∠BFC＝∠BF A＝90°，∵∠ACB＝60°，∠CAB＝45°，∴∠CBF＝30°，∠ABF＝45°＝∠CAB，BC＝2，AF＝BF＝3CF＝23，∴CF＝12∴AC＝CF+AF＝2+23，∵四边形ADCE是平行四边形，AC＝1+3，DO＝EO，∴AO＝CO＝12∴当OD ⊥AB 时，DO 的值最小，即DE 的值最小，则△AOD 是等腰直角三角形，∴OD ＝22AO ＝622+， ∴DE ＝2OD ＝26+．故选：A ．【点评】本题主要考查解直角三角形，平行四边形的性质，掌握平行四边形的性质和特殊角的三角函数值是解题的关键．3．如图，在Rt ABC 中，90,3,4B AB BC ∠=︒==，点D 为BC 上一动点（不与点C 重合），以AD ，CD 为一组邻边作平行四边形ADCE ，当DE 的值最小时，平行四边形ADCE 的周长．．为_____． 【答案】4+213【分析】根据题意，可知当DE ⊥AE 时，DE 取得最小值，然后根据题目中的数据，即可得到A D 、CD 的长，从而可以得到当DE 的值最小时，平行四边形ADCE 周长．【解答】解：当DE ⊥AE 时，DE 取得最小值，设此时CD =x ，∵四边形ADCE 是平行四边形，∴CD =AE ，AD =CE ，BC ∥AE ，∵∠B =90°，DE ⊥AE ，∴四边形BAED 是矩形，∴BD =AE ，∴BD =CD =x ，∵BC =BD +CD ，BC =4，∴BD =CD =2，∵AB =3，∠B =90°，∴AD =22222313BD AB +=+=，∴当DE 的值最小时，平行四边形ADCE 周长为：2+13+2+13=4+213，故答案为：4+213.【点评】本题考查平行四边形的性质、矩形的判定与性质、垂线段最短，解答本题的关键是明确题意，利用数形结合的思想解答． 4．如图，在ABCD 中，=60B ∠︒，10AB =，8BC =，点E 为边AB 上的一个动点，连接ED ，EC ， 以ED 、CE 为邻边构造EDGC ，连接EG ，则EG 的最小值为__________．【答案】83【分析】根据平行四边形的性质得到EG ，FG ，根据垂线段最短得到EG ⊥CD 时取最小值，过点C 作CH ⊥AB 于点H ，求出CH 的长度，从而得到结果．【解答】解：∵四边形EDGC 是平行四边形，∴EF =FG ，∴当EF ⊥CD 时，EF 最小，此时EG 最小，过点C 作CH ⊥AB 于点H ，则CH =EF ，∵∠B =60°，∴∠BCH =30°，∵BC =8，∴BH =4，∴CH =2284-=43，∴EF 的最小值为43，∴EG 的最小值为83，故答案为：83．【点评】本题考查了平行四边形的性质，垂线段最短，直角三角形的性质，勾股定理，解题的关键是理解题意，找到EG最短时满足的条件．5．如图，平行四边形ABCD中，AB＝2，AD＝1，∠ADC＝60°，将平行四边形ABCD沿过点A的直线l 折叠，使点D落到AB边上的点D处，折痕交CD边于点E．若点P是直线l上的一个动点，则PD +PB 的最小值_______．【答案】7【分析】不管P点在l上哪个位置，PD始终等于PD'，故求PD'+PB可以转化成求PD+PB，显然当D、P、D'共线时PD+ PB最短．【解答】过点D作DM⊥AB交BA的延长线于点M，∵四边形ABCD是平行四边形，AD＝1，AB＝2，∠ADC＝60°，∴∠DAM＝60°，由翻折变换可得，AD＝AD′＝1，DE＝D′E，∠ADC＝∠AD′E＝60°，∴∠DAM＝∠AD′E＝60°，∴AD∥D′E，又∵DE∥AB，∴四边形ADED′是菱形，∴点D与点D′关于直线l对称，连接BD交直线l于点P，此时PD′+PB最小，PD′+PB＝BD，在Rt△DAM中，AD＝1，∠DAM＝60°，∴AM=12AD=12，DM=32AD=32，在Rt△DBM中，DM=32，MB＝AB+AM=52，∴BD=DM2+MB2=322+522=7，即PD′+PB最小值为7，故答案为：7．【点评】本题考查平行四边形性质和菱形性质，掌握这些是本题解题关键．6．如图，平行四边形ABCD中，8∠=︒，E是边AD上且2AAD=，60AB=，6=，F是边AB上AE DE+的最小值__________．的一个动点，将线段EF绕点E逆时针旋转60︒，得到EG，连接BG、CG，则BG CG【答案】221【分析】如图，取AB的中点N．连接EN，EC，GN，作EH⊥CD交CD的延长线于H．利用全等三角形的性质证明∠GNB=60°，点G的运动轨迹是射线NG，由“SAS”可证△EGN≌△BGN，可得GB=GE，推出GB+GC=GE+GC≥EC，求出EC即可解决问题．【解答】解：如图，取AB的中点N．连接EN，EC，GN，作EH⊥CD交CD的延长线于H，∵AE=2DE，∴AE=4，DE=2，∵点N是AB的中点，∴AN=NB=4，∴AE=AN，∵∠A=60°，∴△AEN是等边三角形，∴∠AEN=∠FEG=60°，∴∠AEF=∠NEG，∵EA=EN，EF=EG，∴△AEF≌△NEG（SAS），∴∠ENG=∠A=60°，∵∠ANE=60°，∴∠GNB=180°-60°-60°=60°，∴点G的运动轨迹是射线NG，∵BN=EN，∠BNG=∠ENG=60°，NG=NG∴△EGN≌△BGN（SAS），∴GB=GE，∴GB+GC=GE+GC≥EC，在Rt△DEH中，∵∠H=90°，DE=2，∠EDH=60°，DE=1，EH=3，∴DH=12在Rt△ECH中，EC=22221+=，EH CH∴GB+GC≥221，∴GB+GC的最小值为221，故答案为：221．【点评】本题考查旋转变换，轨迹，平行四边形的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考常考题型．7．如图，CD是直线x＝1上长度固定为1的一条动线段．已知A（﹣1，0），B（0，4），则四边形ABCD 周长的最小值为_________________．【答案】17132++【分析】在y轴上取点E，使BE＝CD＝1，则四边形BCDE为平行四边形，根据勾股定理得到AB，作点A关于直线x＝1的对称点A'，得到A'、E、D三点共线时，AD+DE最小值为A'E的长，根据勾股定理求出A'E，即可得解；【解答】解：如图，在y轴上取点E，使BE＝CD＝1，则四边形BCDE为平行四边形，∵B（0，4），A（﹣1，0），∴OB＝4，OA＝1，∴OE＝3，AB＝22+=，1417作点A关于直线x＝1的对称点A'，∴A'（3，0），AD＝A'D，∴AD+DE＝A'D+DE，即A'、E、D三点共线时，AD+DE最小值为A'E的长，在Rt△A'OE中，由勾股定理得A'E＝22+=，3332∴C四边形ABCD最小值＝AB+CD+BC+AD＝AB+CD+A'E＝17+1+32．故答案为：17132++．【点评】本题主要考查了轴对称最短路线问题、勾股定理、位置与坐标，准确分析作图计算是解题的关键．8．如图四边形ABCD，AD∥BC，AB⊥BC，AD＝1，AB＝2，BC＝3，P为AB边上的一动点，以PD，PC 为边作平行四边形PCQD，则对角线PQ的长的最小值是_____．【答案】4【分析】根据题意在平行四边形PCQD中，设对角线PQ与DC相交于点O，可得O是DC的中点，过点Q作QH⊥BC，交BC的延长线于H，易证得Rt△ADP≌Rt△HCQ，即可求得BH=4，则可得当PQ⊥AB 时，PQ的长最小，即为4．【解答】解：在平行四边形PCQD中，设对角线PQ与DC相交于点O，则O是DC的中点，过点Q作QH⊥BC，交BC的延长线于H，∵AD ∥BC ，∴∠ADC=∠DCH ，即∠ADP+∠PDC=∠DCQ+∠QCH ，∵PD ∥CQ ，∴∠PDC=∠DCQ ，∴∠ADP=∠QCH ，又∵PD=CQ ，在Rt △ADP 与Rt △HCQ 中，ADP QCH A QHCPD CQ ⎧⎪⎨⎪∠∠⎩∠∠＝＝＝ ∴Rt △ADP ≌Rt △HCQ （AAS ），∴AD=HC ，∵AD=1，BC=3，∴BH=4，∴当PQ ⊥AB 时，PQ 的长最小，即为4．故答案为：4．【点评】本题考查梯形的中位线的性质，注意掌握梯形的中位线等于两底和的一半且平行于两底．9．如图，四边形ABCD 中，∠B ＝∠D ＝90°，∠C ＝50°，在BC 、CD 边上分别找到点M 、N ，当△AMN 周长最小时，∠AMN ＋∠ANM 的度数为______．【答案】100°【分析】根据要使△AMN 的周长最小，即利用点的对称，让三角形的三边在同一直线上，作出A 关于BC和CD 的对称点A′，A″，即可得出∠AA′M+∠A″=180°-∠DAB =∠C=50°，进而得出∠AMN+∠ANM=2（∠AA′M+∠A″）即可得出答案．【解答】解：作A 关于BC 和CD 的对称点A′，A″，连接A′A″，交BC 于M ，交CD 于N ，则A′A″即为△AMN 的周长最小值．∵∠B ＝∠D ＝90°，∠C ＝50°，∵∠DAB=130°，∴∠AA′M+∠A″=180°-130°=50°，由对称性可知：∠MA′A=∠MAA′，∠NAD=∠A″，且∠MA′A+∠MAA′=∠AMN ，∠NAD+∠A″=∠ANM ，∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2（∠AA′M+∠A″）=2×50°=100°，故答案为：100°．【点评】此题主要考查了平面内最短路线问题求法以及三角形的内角和定理及外角的性质和轴对称的性质等知识，根据已知得出M ，N 的位置是解题关键．10．如图，在ABCD 中，对角线AC 、BD 相交于点O ，点E 、F 分别是边AD 、AB 上的点，连结OE 、OF 、EF ．若7AB =，52BC =，45DAB ∠=︒，则OEF 周长的最小值是_______．【答案】1322【分析】作点O 关于AB 的对称点M ，点O 关于AD 的对称点N ，连接MN 交AB 于F ，交AD 于E ，此时△OEF 的周长最小，周长的最小值＝MN ，由作图得AN ＝AO ＝AM ，∠NAD ＝∠DAO ，∠MAB ＝∠BAO ，于是得到∠MAN ＝90°，过D 作DP ⊥AB 于P ，则△ADP 是等腰直角三角形，根据等腰直角三角形的性质得到AP ＝DP ＝22AD ，求得AP ＝DP ＝5，根据三角形的中位线的性质得到OQ ＝12DP ＝52，BQ ＝12BP＝12（AB−AP ）＝1，根据勾股定理求出AO ＝132，然后根据等腰直角三角形的性质即可得到结论． 【解答】解：作点O 关于AB 的对称点M ，点O 关于AD 的对称点N ，连接MN 交AB 于F ，交AD 于E ，此时△OEF 的周长最小，周长的最小值＝MN ，∴AN ＝AO ＝AM ，∠NAD ＝∠DAO ，∠MAB ＝∠BAO ，∵∠DAB ＝45°，∴∠MAN ＝90°，过D 作DP ⊥AB 于P ，则△ADP 是等腰直角三角形，∴AP ＝DP ＝22AD ， ∵AD ＝BC ＝52，∴AP ＝DP ＝5，设OM ⊥AB 于Q ，则OQ ∥DP ，∵OD ＝OB ，∴OQ ＝12DP ＝52，BQ ＝12BP ＝12（AB−AP ）＝1， ∴AQ ＝6，∴AO ＝2222513622AQ OQ ， ∴AM ＝AN ＝AO ＝132， ∴MN ＝2AM ＝1322， ∴△OEF 周长的最小值是1322． 故答案为：1322． 【点评】此题主要考查轴对称−−最短路线问题，平行四边形的性质，等腰直角三角形的性质，勾股定理以及三角形中位线定理等，正确的作出辅助线是解题的关键．11．如图，点(1,3),(6,1),(,0),(2,0)A B P a N a --+为四边形的四个顶点，当四边形PABN 的周长最小时，=a ________．【答案】13 4【分析】作点A关于x轴的对称点A′，则A′（1，3），将A′向右平移2个单位，即A″（3，3），连接A″B，与x轴交于点N，可判断出AP+BN=A″N+BN≥A″B，即此时四边形ABNP的周长最小，求出A″B的表达式，得到与x轴的交点，即为点N，从而可得a值．【解答】解：如图，作点A关于x轴的对称点A′，则A′（1，3），将A′向右平移2个单位，即A″（3，3），连接A″B，与x轴交于点N，则此时AP=A′P=A″N，则AP+BN=A″N+BN≥A″B，在四边形ABNP中，PN和AB均为定值，∴此时四边形ABNP的周长最小，设A″B的表达式为y=kx+b，则3361k bk b+=⎧⎨+=-⎩，解得：437kb⎧=-⎪⎨⎪=⎩，∴直线A″B的表达式为473y x=-+，令y=0，则214x=，即此时N（214，0），2124a+=，解得：a=134，故答案为：134． 【点评】本题考查了轴对称-最短路线问题：通过对称，把两条线段的和转化为一条线段，利用两点之间线段最短解决问题．12．如图，在四边形ABCD 中，90,5,4,A D AB AD ∠=∠=︒==3,CD =点P 是边AD 上的动点，则PBC 周长的最小值为（ ）A ．8B ．45C ．12D ．65【答案】D【分析】根据勾股定理可求BC 的长，所以要使△PBC 的周长最小，即BP+PC 最短，利用对称性，作点C 关于AD 的对称点E ，即可得出最短路线，从而求解可．【解答】解：过点C 作CG ⊥AB ，由题意可知四边形DAGC 是矩形∴CG=AD=4，BG=AB-AG=AB-CD=2∴在Rt △BCG 中，222425BC =+=作点C 关于AD 的对称点E ，连接BE ，交AD 于点P'，连接'CP此时'P BC 的周长为最小值，即''''BP CP BC BP EP BC BE BC ++=++=+过点E 作EF ⊥BA ，交BA 的延长线于点F由题意可知四边形EFAD 为矩形∴EF=AD=4，DE=CD=AF=3∴在Rt △EBF 中，224(35)45BE =++=∴此时'P BC 的周长为：65BE BC +=故选：D ．【点评】本题考查勾股定理解直角三角形及应用对称的性质求最短路线，掌握相关性质定理正确添加辅助线进行推理计算是解题关键．13．如图，四边形ABCD 为平行四边形，延长AD 到点E ，使DE AD =，且BE DC ⊥．(1)求证：四边形DBCE 为菱形；(2)若DBC △是边长为2的等边三角形，点P 、M 、N 分别在线段BE 、BC 、CE 上运动，求PM PN +的最小值． 【答案】(1)证明见解析(2)3【分析】（1）先根据四边形ABCD 为平行四边形的性质和DE AD =证明四边形DBCE 为平行四边形，再根据BE DC ⊥，即可得证；（2）先根据菱形对称性得，得到'PM PN PM PN +=+，进一步说明PM PN +的最小值即为菱形的高，再利用三角函数即可求解．（1）证明：∵四边形ABCD 是平行四边形，∴AD BC ∥，AD BC =，∵DE AD =，∴DE BC =，又∵点E 在AD 的延长线上，∴DE BC ∥，∴四边形DBCE 为平行四边形，又∵BE DC ⊥，∴四边形DBCE 为菱形．（2）解：如图，由菱形对称性得，点N 关于BE 的对称点'N 在DE 上，∴'PM PN PM PN +=+，当P 、M 、'N 共线时，''PM PN PM PN MN +=+=，过点D 作DH BC ⊥，垂足为H ，∵DE BC ∥，∴'MN 的最小值即为平行线间的距离DH 的长，∵DBC △是边长为2的等边三角形，∴在Rt DBH 中，60DBC ∠=︒，2DB =，sin DH DBC DB ∠=， ∴3sin 232DH DB DBC =∠=⨯=， ∴PM PN +的最小值为3．【点评】本题考查了最值问题，考查了菱形的判定和性质，平行四边形的判定和性质，三角函数等知识，运用了转化的思想方法．将最值问题转化为求菱形的高是解答本题的关键．14．如图，在平行四边形ABCD 中，2,1,60AB AD B ==∠=︒，将平行四边形ABCD 沿过点A 的直线l 折叠，使点D 落到AB 边上的点'D 处，折痕交CD 边于点E ．（1）求证：四边形'BCED 是菱形；（2）若点P 是直线l 上的一个动点，请作出使'PD PB +为最小值的点P ，并计算'PD PB +．【答案】（1）见解析；（2）作图见解析，7得到DAD E'是菱形，作DG BA⊥）将ABCD沿过点A的直线∠=EA，D//DE AD∴∠=DEA∴∠=，DAE EA∴∠'DAD∴四边形=AD ADAB=，2∴=AD AD∴'是菱形；BCED（2）四边形∴与D'D连接BD交CD AB//∴∠=DAGAD=，112AG ∴=，32DG =， 52BG ∴=， 227BD DG BG ∴=+=，PD PB ∴'+的最小值为7．【点评】本题考查了平行四边形的性质，最短距离问题，勾股定理，菱形的判定和性质，正确的作出辅助线是解题的关键．。

四边形最值问题解题技巧
1.确定四边形属性：确定四边形属性很重要，四边形属性指的是四边
形的特定性质，例如是否是矩形或平行四边形等。

根据属性分析，可以推
断出四边形其他性质，例如角度、边长等。

2.利用角度性质：四边形的角度性质非常重要，利用它可以得到很多
信息。

例如，矩形四个角度都是90度，对角线相等，平行四边形对角线
交点的角度相等等。

3.应用相似三角形：当四边形有相似三角形时，可以用相似三角形的
性质来解题。

例如，平行四边形的对角线交点分割成的四个三角形都是相
似的三角形，利用相似三角形的比例可以得到四边形的一些边长。

4.利用面积公式：四边形的面积公式有很多，其中最常用的是矩形和
平行四边形的面积公式。

利用面积公式可以得到四边形的面积，此时需要
注意单位统一。

5.利用勾股定理：当四边形是矩形或正方形时，可以利用勾股定理解题。

例如，矩形的对角线是勾股定理中的斜边，可以利用勾股定理求出其
长度。

6.利用平面几何知识：除了以上方法，还可以利用平面几何知识解题，例如平行线之间的夹角相等、对顶角相等等。

利用这些知识可以得到四边
形的一些性质。

人教版数学八年级下期第十八章平行四边形最值问题训练一、选择题1.如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（）A. 1B. 1C. 2D. 222.如图，已知菱形ABCD的边长为6，点M是对角线AC上的一动点，且∠ABC=120°，则MA+MB+MD的最小值是( )A. 33B. 3+33C. 6+3D. 633.如图，在矩形ABCD中，AB=3，BC=4，在矩形内部有一动点P满足S△PAB=3S△PDC，则动点P到点A，B两点距离之和PA+PB的最小值为（）A. 5B. 35C. 3+32D. 2134.如图，在边长为4的菱形ABCD中，BD＝4，E、F分别是AD、CD上的动点（包含端点），且AE+CF＝4，连接BE、EF、FB．则EF的最大值与最小值分别为（）A. 4，2B. 4，23C. 5，3D. 5，325.如图，点P是正方形ABCD的边AD上的一动点，正方形的边长为4，点P到正方形的两条对角线AC和BD的距离分别为PM,PN,则PM2+PN2的最小值为（）A. 2B. 4C. 9D. 126.如图，四边形ABCD是菱形，AB＝8，且∠ABC＝60°，M为对角线BD（不含B点）BM的最小值为( )上任意一点，则AM+12A. 43B. 33C. 42D. 32二、填空题7.如图，P为菱形ABCD的对角线上一点，PF⊥AD于F，PF=3cm，点E为AB边上一动点，则PE的最小值为______cm．8.如图，在边长为4的菱形ABCD中，∠A＝60°，若M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C的最小值为 .9.如图，在菱形ABCD中，∠ABC=60°，AB=8，点M、N分别在边AB、CD上，且AM=2，DN=4，点P、Q分别为BC、AD上的动点，连接PM、PN、PQ，则PM+PN+PQ 的最小值为______．10.如图，长方形ABCD中，AB=6，BC=4，在长方形的内部以CD边为斜边任意作Rt△CDE，连接AE，则线段AE长的最小值是_____．11.如图，在矩形ABCD中，AB=3，AD=10，点E在AD上且DE=2．点G为AE的中点，点P为BC边上的一个动点，F为EP的中点，则GF+EF的最小值为________.12.如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为4，则线段DH长度的最小值是____．三、解答题13.如图，在边长为m的菱形ABCD中，∠DAB=60°，E是AD上不同于A，D两点的一动点，F是CD上一动点，且AE+CF=m．（1）证明：无论E，F怎样移动，△BEF总是等边三角形；（2）求△BEF面积的最小值．14.如图，在菱形ABCD中，AB=6，∠ADC=120°，P为对角线AC上的一点，过P作PE∥AB交AD与E，PF∥AD交CD于F，连接BE、BF、EF（1）求AC的长；（2）求证：△BEF为等边三角形；（3）四边形BEPF面积的最小值为______15.如图1，四边形ABCD是矩形，点O位于对角线BD上，将△ADE，△CBF分别沿DE、BF翻折，点A，点C都恰好落在点O处．（1）求证：∠EDO=∠FBO；（2）求证：四边形DEBF是菱形：（3）如图2，若AD=2，点P是线段ED上的动点，求2AP+DP的最小值．16.如图，在矩形ABCD中，AD=2AB，E是边AD的中点，F是边AB上的一个动点，连结EF，过点E作EG⊥EF交BC于点G．（1）求证：EF=GE；（2）若AB=1，则AF+EF+CG的最小值为______．17.如图，正方形ABCD的边长为25，O是BC边的中点，P是正方形内一动点，且OP=2，连接DP，将线段DP绕点D逆时针旋转90°到DQ，连接AP，CQ．（1）直接写出线段AP和CQ的关系．（2）当A，O，P三点共线时，求线段DP的长．（3）连接PQ，求线段PQ的最小值．18.如图，菱形ABCD中，∠B＝60°，点E在边BC上，点F在边CD上．（1）如图1，若E是BC的中点，∠AEF＝60°，求证：BE＝DF；（2）如图2，若∠EAF＝60°，求证：△AEF是等边三角形；（3）在（2）的条件下，如果AB＝10，那么△AEF的周长是否存在最小值？如果存在，请求出来．参考答案1.B2.D3.B4.B5.B6.A7.38.27-29.231+4310.211.512.25-213.解：（1）连接BD，∵∠DAB=60°，∴△ABD是等边三角形，∴AB=DB，又∵AE+CF=m，∴AE=DF，在△ABE 和△DBF 中AB =DB ∠A =∠BDF =60°AE =DF，∴△ABE ≌△DBF （SAS ），∴BE =BF ∴∠EBF =∠ABD =60°，∴△BEF 是等边三角形．（2）当BE ⊥AD 时面积最小，此时BE =m 2−(12m )2=32m ，△BEF 的EF 边上的高=(32m )2−(34m )2=34m ，S △BEF =12×32m ×34m =3163m 2．14.解：（1）连接BD ，交AC 于G ，∵菱形ABCD 中，AC 和BD 是对角线，∴BD ⊥AC ，AG =CG =12AC ，∵AB =6，∠ADC =120°，∴∠BAC =∠BCA =30°，在Rt △ABG 中，AG =AB •cos ∠BAC =6×32=33，∴AC =2AG =63；（2）证明：∵在菱形ABCD 中，AB =6，∠ADC =120°，∴∠BAD =∠BCD =60°，∠ABD =∠CBD =∠ADB =∠CDB =60°，∴△ABD 是等边三角形，∴BD =AB =BC =6，∵PE ∥AB ，PF ∥AD ，∴∠CPF =∠CAD ，四边形DEPF 是平行四边形，∴ED =PF ，∵AD =DC ，∴∠CAD =∠ACD ，∴∠CPF =∠ACD ，∴PF =FC ，∴ED =FC ，在△BED 和△BFC 中ED =FC ∠EDB =∠FCB =60°BD =BC∴△BED ≌△BFC （SAS ），∴BE =BF ，∠EBD =∠FBC ，∵∠FBC +∠FBD =∠CBD =60°，∴∠EBD +∠FBD =∠EBF =60°，∴△BEF 是等边三角形；（3）93215.（1）证明：∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠ADB =∠CBD ，∵将△ADE ，△CBF 分别沿DE 、BF 翻折，点A ，点C 都恰好落在点O 处．∴△ADE ≌△ODE ，∴△CFB ≌△OFB ，∴∠ADE =∠ODE =12∠ADB ，∠CBF =∠OBF =12∠CBD ，∴∠EDO =∠FBO ；（2）证明：∵∠EDO =∠FBO ，∴DE ∥BF ，∵四边形ABCD 是矩形，∴AB ∥CD ，AD =BC ，∠A =90°，∵DE ∥BF ，AB ∥CD ，∴四边形DEBF 是平行四边形，又∵△ADE △≌△ODE ，∴∠A =∠DOE =90°，∴EF ⊥BD ，∴四边形DEBF 是菱形；（3）解：过点P 作PH ⊥AD 于点H ，∵四边形DEBF是菱形，△ADE≌△ODE，∴∠ADE=∠ODE=∠ODF=30°，∴在Rt△DPH中，2PH=PD，∴2AP+PD=2PA+2PH=2（AP+PH），过点O作OM⊥AD，与DE的交点即是2AP+PD的值最小的点P的位置．而此时（2AP+PD）的最小值=2OM，∵△ADE≌△ODE，AD=2，∴AD=DO=2，在Rt△OMD中，∵∠ODA=2∠ADE=60°，∴∠DOM=30°，∴DM=12DO=1，∵DM2+OM2=DO2，∴12+OM2=22，∴OM=3，∴（2PA+PD）的最小值为2OM=23．16.217.解：（1）AP=CQ，AP⊥CQ；理由如下：延长QC、AP交于点E，AP的延长线交BC于F，如图1所示：∵四边形ABCD是正方形，∴AD=CD，∠ADC=∠BCD=90°，AD∥BC，由旋转的性质得：∠PDQ=90°，DP=DQ，∴∠ADP=∠CDQ，在△ADP和△CDQ中，AD=CD∠ADP=∠CDQDP=DQ，∴△ADP≌△CDQ（SAS），∴AP=CQ，∠DAP=∠DCQ，∵∠BCD=90°，∴∠DCQ+∠ECF=90°，∵AD∥BC，∴∠DAP=∠CFE，∴∠CFE+∠ECF=90°，∴∠CEF=90°，∴AE⊥QE，∴AP⊥CQ；（2）作DH⊥AP于H，如图2所示：∵O是BC边的中点，∴OB=12BC=5，当A，O，P三点共线时，由勾股定理得：AO=AB2+OB2=(25)2+(5)2=5，∵四边形ABCD是正方形，∴∠B=90°，AD∥BC，∴∠DAH=∠BOA，∴sin∠DAH=sin∠BOA=ABAO =255，cos∠DAH=cos∠BOA=OBAO=55，∴DH=AD×sin∠DAH=25×255=4，AH=AD×cos∠DAH=25×55=2，∴PH=AO-AH-OP=5-2-2=1，∴DP=42+12=17；（3）连接OD，如图3所示：∵DQ=DP，∠PDQ=90°，∴PQ=2DP，OD=DC2+OC2=(25)2+(5)2=5，∵OP+DP≥OD，∴DP≥OD-OP=5-2=3，∴PQ≥32，∴线段PQ的最小值为32．18.证明：（1）如图1，连接AC，∵在菱形ABCD中，∠B=60°，∴AB=BC=CD，∠C=180°-∠B=120°，∴△ABC是等边三角形，∵E是BC的中点，∴AE⊥BC，∵∠AEF=60°，∴∠FEC=90°-∠AEF=30°，∴∠CFE=180°-∠FEC-∠ECF=180°-30°-120°=30°，∴∠FEC=∠CFE，∴EC=CF，∴BE=DF；（2）如图2，连接AC，∵△ABC是等边三角形，∴AB=AC，∠ACB=60°，∴∠B=∠ACF=60°，∵AD∥BC，∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD，∠AFC=∠D+∠FAD=60°+∠FAD，∴∠AEB=∠AFC，在△ABE和△ACF中，∠B=∠ACF∠AEB=∠AFC，AB=AC∴△ABE≌△ACF（AAS），∴AE=AF，∵∠EAF=60°，∴△AEF是等边三角形．（3）由垂线段最短可知：当AE⊥BC时，AE有最小值．∵AE⊥BC，∠B＝60°，∴AE AB =32．∴AE＝10×32＝53．∴△AEF周长的最小值为3×53＝153．。

特殊四边形中的最值问题题型一矩形中的最值问题1．（2020•鄂州模拟）如图，矩形ABCD中，AB＝10，BC＝5，点E，F，G，H分别在矩形ABCD各边上，且AE＝CG，BF＝DH，则四边形EFGH周长的最小值为10√5．【详解】解：作点E关于BC的对称点E′，连接E′G交BC于点F，此时四边形EFGH周长取最小值，过点G作GG′⊥AB于点G′，如图所示．∵AE＝CG，BE＝BE′，∴E′G′＝AB＝10，∵GG′＝AD＝5，∴E′G=√E′G′2+GG′2=5√5，∴C四边形EFGH＝2E′G＝10√5．故答案为：10√5．2．（2020•泗阳县校级期中）如图，在矩形ABCD中，AB＝3，BC＝4，P是AB上动点，PQ平行于BC交CD于Q．M是AD上动点，MN平行于AB交BC于N．则PM+NQ的最小值为5．【详解】解：如图，设PQ交MN于F，连接AF、CF、AC．∵四边形ABCD是矩形，PQ∥BC，MN∥AB，∴可得四边形APFM、四边形CQFN是矩形，∴PM＝AF，NQ＝CF，∴PM+CQ＝AF+CF，∵F A+FC≥AC，AC=√32+42=5，∴AF+FC的最小值为5，∴PM+NQ的最小值为5．故答案为53．（2020•沙坪坝区校级月考）如图，在矩形ABCD中，AD＝4√3，∠DAC＝30°，点P、E分别在AC、AD上，则PE+PD的最小值是6．【详解】解：作D关于直线AC的对称点D′，过D′作D′E⊥AD于E，则D′E＝PE+PD的最小值，∵四边形ABCD是矩形，∴∠ADC＝90°，∵AD＝4√3，∠DAC＝30°，∵DD′⊥AC，∴∠CDD′＝30°，∴∠ADD′＝60°，∴DD′＝4√3，∴D′E＝6，故答案为：6．题型二菱形中的最值问题4．（2020•西城区校级期中）如图，菱形ABCD的对角线AC＝12，面积为24，△ABE是等边三角形，若点P在对角线AC上移动，则PD+PE的最小值为（）A．4B．4√2C．2√10D．6【详解】解：如图，连接BD交AC于O，连接PB．∵S菱形ABCD=12•AC•BD，∴24=12×12×BD，∴BD＝4，∵OA=12AC＝6，OB=12BD＝2，AC⊥BD，∴AB=√62+22=2√10，∵AC与BD互相垂直平分，∴PD＝PB，∴PE+PD＝PE+PB，∵PE+PB≥BE，∴当E、P、B共线时，PE+PD的值最小，最小值为BE的长，∵△ABE是等边三角形，∴BE＝AB＝2√10，∴PD+PE的最小值为2√10，故选：C．5．（2020•蓝田县一模）如图，菱形ABCD的边长为3，∠BAD＝60°，点E、F在对角线AC上（点E在点F的左侧），且EF＝1，则DE+BF最小值为√10【详解】解：如图，作DM∥AC，使得DM＝EF＝1，连接BM交AC于F，∵DM＝EF，DM∥EF，∴四边形DEFM是平行四边形，∴DE＝FM，∴DE+BF＝FM+FB＝BM，根据两点之间线段最短可知，此时DE+FB最短，∵四边形ABCD是菱形，AB＝3，∠BAD＝60°∴AD＝AB，∴△ABD是等边三角形，∴BD＝AB＝3，在Rt△BDM中，BM=√12+32=√10∴DE+BF的最小值为√10．故答案为√10．6．（2020•武昌区期中）如图，已知平行四边形ABCD中，AB＝BC，BC＝10，∠BCD＝60°，两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动，连接OA，则OA的长的最小值是5√3−5．【详解】解：如图所示：过点A作AE⊥BD于点E，当点A，O，E在一条直线上，此时AO最短，∵平行四边形ABCD中，AB＝BC，BC＝10，∠BCD＝60°，∴AB＝AD＝CD＝BC＝10，∠BAD＝∠BCD＝60°，∴△ABD是等边三角形，∴AE过点O，E为BD中点，则此时EO＝5，故AO的最小值为：AO＝AE﹣EO＝AB sin60°−12×BD＝5√3−5．故答案为：5√3−5题型三正方形中的最值问题7．（2020•洛阳三模）如图，点E、F是边长为4的正方形ABCD边AD、AB上的动点，且AF＝DE，BE交CF于点P，在点E、F运动的过程中，P A的最小值为（）A．2B．2√2C．4√2−2D．2√5−2【详解】解：在正方形ABCD中，∴AB＝BC，∠BAE＝∠ABC＝90°，在△ABE和△BCF中，∵{AB=BC∠BAE=∠ABCAE=BF，∴△ABE≌△BCF（SAS），∴∠ABE＝∠BCF，∵∠ABE+∠CBP＝90°∴∠BCF+∠CBP＝90°∴∠BPC＝90°如图，取BC的中点O，连接OP、OA，则OP=12BC＝2，在Rt△AOB中，OA=√AB2+OB2=√22+42=2 √5，根据三角形的三边关系，OP+AP≥OA，∴当O、P、A三点共线时，AP的长度最小，AP的最小值＝OA﹣OP＝2 √5−2．故选：D．8．（2020•永登县期中）如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为2√3．【详解】解：连接BD，与AC交于点F．∵点B与D关于AC对称，∴PD＝PB，∴PD+PE＝PB+PE＝BE最小．∵正方形ABCD的面积为12，∴AB＝2√3．又∵△ABE是等边三角形，∴BE＝AB＝2√3．故所求最小值为2√3．故答案为：2√3．巩固练习1．（2020•鸡泽县期末）如图，将n 个边长都为2的正方形按如图所示摆放，点A 1，A 2，…A n 分别是正方形的中心，则这n 个正方形重叠部分的面积之和是（ ）A ．nB ．n ﹣1C ．4（n ﹣1）D ．4n 【详解】解：由题意可得一个阴影部分面积等于正方形面积的14，即是14×4＝1，n 个这样的正方形重叠部分（阴影部分）的面积和为：1×（n ﹣1）＝n ﹣1．故选：B ．2．（2020•庐阳区校级月考）如图，在菱形ABCD 中，AB ＝4，E 是AB 边上一点，且∠A ＝∠EDF ＝60°，有下列结论：①△DEF 是等边三角形；②∠ADE ＝∠BEF ；③△BEF 周长的最小值为4+2√3，④△BEF 面积的最小值为√3．其中正确结论有（ ）A ．1个B ．2个C ．3个D ．4个【详解】解：连接BD ，∵菱形ABCD 中，∠A ＝60°，∴△ADB 与△CDB 是等边三角形，∴∠DBE ＝∠C ＝∠60°，BD ＝DC ，∵∠EDF ＝60°，∴∠BDE ＝∠CDF ，在△BDE 和△CDF 中∠DBE ＝∠C ，∠BDE ＝∠CDF ，BD ＝CD ，∴△DBE≌△DCF，∴DE＝DF，∠BDE＝∠CDF，BE＝CF，∴∠EDF＝∠BDC＝60°，∴△DEF是等边三角形，故①正确；∴∠DEF＝60°，∴∠AED+∠BEF＝120°，∵∠AED+∠ADE＝180°﹣∠A＝120°，∴∠AED+∠BEF ＝∠AED+∠ADE，即∠ADE＝∠BEF，故②正确；∵△BEF的周长＝BE+BF+EF＝BF+CF+EF＝BC+EF＝4+EF，∴等边三角形△DEF的边长最小时，△BEF 的周长最小，当DE⊥AB时，DE最小＝2√3△BEF周长的最小值为4+2√3，故③正确；连接BD，AC，∵菱形ABCD边长为4，∠BAD＝60°；∴△ABD与△BCD为正三角形，∴∠FDB＝∠EAB＝60°，∵AE+CF＝4，DF+CF＝4，∴AE＝DF，∵AB＝BD，∴△BDF≌△BAE，∴BE＝BF，∠ABE＝∠DBF，∴∠EBF＝∠ABD＝60°，∴△BEF是等边三角形，∴当BE⊥AD时，△BEF的面积最小，此时BE=√3，△BEF面积的最小值＝3√3，故④错误；综上正确的有①②③共3个．故选：C．3．如图，点P是矩形ABCD对角线BD上的一个动点，已知AB＝2，BC=√3，则P A+PB+PC的最小值是√13．【详解】解：将△PBC绕点C逆时针旋转60°，得到△EFC，连接PE，BF，则EF＝PB，△PCE是等边三角形，△BFC是等边三角形，∴PE＝PC，∴P A+PB+PC＝P A+PE+EF，当P A、PE、EF共线时，值最小，连接BF，作FN⊥BC，延长BM＝FN，连接MF，则四边形BMFN是矩形，∴BM＝FN，MF＝BN，∵△BCF是等边三角形，∴FN=√32BF=√32BC=√32×√3=32，BN=12BF=12BC=√32，∴AM＝AB+BM＝2+32=72，MF=√32，∴AF=√AM2+MF2=√13，∴P A+PB+PC的最小值为√13，故答案为√13．4．（2020•荔湾区校级模拟）如图，在正方形ABCD中，点E是BC上的一定点，且BE＝5，EC＝7，点P 是BD上的一动点，则PE+PC的最小值是13．【详解】解：如图连接AE交BD于P点，则AE就是PE+PC的最小值，∵正方形ABCD中，点E是BC上的一定点，且BE＝5，EC＝7，∴AB＝12，∴AE=√122+52=13，∴PE+PC的最小值是13．故答案为：13．5．如图，在矩形ABCD中，AB长为4，BC长为5，F是CD上的一点，且CF＝1，点E在AD上，且BE+EF最小，则DE长为157．【详解】解：作B关于AD的对称点G，连接GF交AD于E，则此时，BE+EF最小，AG＝AB＝4，∵四边形ABCD是矩形，∴CD＝AB＝4，AD＝BC＝5，∵CF＝1，∴DF＝3，∵AG∥DF，∴△AGE∽△DEF，∴AGDF =AEDE，∴43=5−DEDE，解得：DE=157，故答案为：157．6．（2020•新城区校级期中）如图，已知，在矩形ABCD中，AD＝4，AB＝8，点E，F是边CD上的动点（点F在点E右侧），且EF＝2，则四边形ABFE周长的最小值为20．【详解】解：在AB上截取AA′＝EF，作点A′关于直线DC的对称点A″，连接BA″交CD于F，此时四边形AEFB的周长最小．四边形AEFB的周长的最小值＝AB+EF+AE+BF＝AB+EF+A′F+BF＝AB+CD+A″F+BF＝AB+EF+A″B ＝8+2+√82+62=20，故答案为20．7．（2020•武昌区期中）如图，四边形ABCD是菱形，AB＝6，且∠ABC＝60°，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM的最小值为6√3．【点睛】如图，将△ABM绕点B逆时针旋转60°得到△EBN，连接MN，作EF⊥CB交CB的延长线于点F．根据“两点之间线段最短”，当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长．【详解】解：如图，将△ABM绕点B逆时针旋转60°得到△EBN，连接MN，AE，EC．作EF⊥CB交CB的延长线于点F．∵△ABE是等边三角形，∴BA＝BE，∠ABE＝60°．∵∠MBN＝60°，∴∠MBN﹣∠ABN＝∠ABE﹣∠ABN．即∠MBA＝∠NBE．又∵MB＝NB，∴△AMB≌△ENB（SAS），∴AM＝EN，∵∠MBN＝60°，MB＝NB，∴△BMN是等边三角形．∴BM＝MN．∴AM+BM+CM＝EN+MN+CM．根据“两点之间线段最短”，得EN+MN+CM＝EC最短∴当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长，过E点作EF⊥BC交CB的延长线于F，∴∠EBF＝180°﹣120°＝60°，∵BC＝AB＝BE＝6，∴BF＝3，EF＝3√3，在Rt△EFC中，∵EF2+FC2＝EC2，EC＝6√3．故答案为：6√3．。

特殊四边形中的最值问题张萌一、菱形中的最值问题例1（2014年莆田,改编）如图1，四边形ABCD 为菱形，∠BAD =120°， 点E 是AB 的中点，点F 是AC 上的一动点.如果EF+BF 的最小值是28，那么菱形的边长为_______.解：连接EC ，ED .因为菱形ABCD 关于AC 所在的直线对称，所以点D 是点B 关于AC的对称点，所以ED 为EF+BF 的最小值.因为∠BAD =120°，所以∠ABC =60°.又因为BA=BC ，所以△ABC 为等边三角形.又因为点E 是AB 的中点，所以CE ⊥AB ，∠CEB =90°.因为AB ∥CD ，所以∠ECD =90°.设菱形的边长为x . 在Rt △BEC 中，2222212CE BC BE x x ⎛⎫=-=- ⎪⎝⎭. 在Rt △ECD 中，2222(28)ED CE CD =+=，即22221(28)2x x x ⎛⎫-+= ⎪⎝⎭，解得4x =（负值舍去）.所以菱形的边长为4.二、矩形中的最值问题例2如图2，∠MON =90°，矩形ABCD 的顶点A ，B 分别在边OM ，ON上，当B 在边ON 上运动时，A 随之在OM 上运动，矩形ABCD 的形状保持不变，其中AB =2，BC =1，运动过程中，点D 到点O 的最大距离为_______. 解：如图2，取AB 的中点E ，连接OD,OE ,DE.因为∠MON =90°，AB=2，所以OE=AE =12AB =1.(直角三角形斜边上的中线等于斜边的一半)因为四边形ABCD 是矩形，BC =1，所以AD=BC =1.所以DE =22AD AE +=2211+=2.根据三角形的三边关系，OD ＜OE +DE ，所以当OD 过点E 时最大，最大值为2+1三、正方形中的最值问题例3（2014年资阳）如图3，在边长为4的正方形ABCD 中，E 是AB 边上的一点，且AE =3，点Q 为对角线AC 上的动点，则△BEQ 周长的最小值为________.解：连接DE ．因为四边形ABCD 是正方形，所以点B 与点D 关于直线AC 对称.所以DE 的长即为BQ +QE 的最小值．因为DE ＝22AD AE +＝2243+＝5， 所以△BEQ 周长的最小值为DE +BE ＝5+1＝6. 图1图3图2。