02第二章 控制系统的数学描述1
- 格式:ppt
- 大小:1.67 MB
- 文档页数:70








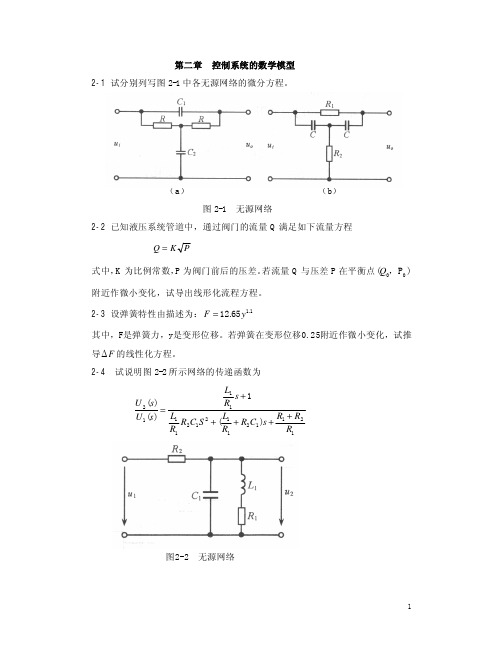
第二章 控制系统的数学模型2-1 试分别列写图2-1中各无源网络的微分方程。
(a ) (b )图2-1 无源网络2-2 已知液压系统管道中,通过阀门的流量Q 满足如下流量方程P K Q =式中,K 为比例常数,P 为阀门前后的压差。
若流量Q 与压差P 在平衡点)P (00,Q 附近作微小变化,试导出线形化流程方程。
2-3 设弹簧特性由描述为:1.165.12y F =其中,F 是弹簧力,y 是变形位移。
若弹簧在变形位移0.25附近作微小变化,试推导F Δ的线性化方程。
2-4 试说明图2-2所示网络的传递函数为1211211212111112)(1)()(R R R s C R R L S C R R L s R L s U s U +++++=图2-2 无源网络2-5 求图2-3所示有源网络的传递函数。
图2-3 有源网络2-6 试证明图2-4(a)的电网络与(b)的机械系统有相同的数学模型。
图2-4 电网络与机械系统2-7 由运算放大器组成的控制系统模拟电路如图2-5所示,试求闭环传递函数 )()(s U s U r c 。
图2-5 控制系统模拟电路2-8 某位置随动系统原理方块图如图2-6所示。
已知电位器最大工作角度o 330max =θ,功率放大级放大系数为K3,要求:(1) 分别求出电位器传递系数K0、第一级和第二级放大器的比例系数K1和K2;(2) 画出系统结构图;(3) 简化结构图,求系统传递函数)(/)(0s s i θθ。
图2-6 位置随动系统原理图2-9 已知一系统由如下方程组组成,试绘制系统结构图并求闭环传递函数)()(s R s C[])()()()()()()(87111s C s G s G s G s R s G s X −−=[])()()()()(36122s X s G s X s G s X −=[])()()()()(3523s G s C s G s X s X −=)()()(34s X s G s C =2-10 已知控制系统结构图如图2-7所示。








