6-2交互作用双因子方差分析解读
- 格式:ppt
- 大小:551.50 KB
- 文档页数:35

统计与决策2021年第1期·总第565期摘要:文章引入虚拟变量,将带交互作用的双因素方差分析进行了线性回归模型重构,给出了模型的参数估计,证明了回归分析的误差分解与方差分析的离差分解是一致的,得出方差分析的因素显著性F 检验与回归模型的显著性检验的等价性。
同时对方差分析的多重比较t 检验和线性模型的回归系数检验做了比较,指出了他们之间的联系和差异性,分析了差异来源是由于样本的选择差异,最后通过实例给出了两种方法的具体实现。
关键词:方差分析;多元线性回归;虚拟变量;多重比较中图分类号:O212.1文献标识码:A 文章编号:1002-6487(2021)01-0010-05带交互作用的双因素方差分析的线性回归建模黄伯强1,李启才2(1.南京师范大学中北学院;2.南京师范大学数学科学学院,南京210023)基金项目:国家自然科学基金资助项目(11701288);南京师范大学青蓝工程项目(2016);南京师范大学中北学院优秀教学团队建设项目(2018jxtd007)作者简介:黄伯强(1981—),男,江苏宜兴人,硕士,讲师,研究方向:概率论与数理统计。
李启才(1979—),男,安徽东至人,博士,副教授,研究方向:随机控制理论及其应用。
0引言方差分析与回归分析是数理统计中重要的两种统计方法,方差分析主要用来讨论不同试验因素对结果的影响是否存在差异性,分为单因素方差分析与双因素方差分析;回归分析是研究自变量与因变量之间函数关系的模型,比较常见的是线性回归模型。
一般的统计学教材都是单独介绍这两个内容,但这两种统计方法存在一定的相互关系。
许多学者对此做过研究,如刘晓华等(2012)讨论了单因素方差分析与虚拟变量回归,研究了这两种方法下显著性差异检验的等价性,但没有给出双因素方差分析下的回归建模;傅莺莺等(2019)将单因素方差分析纳入线性回归的理论体系,给出了回归系数的几何解释,并比较了单因素方差分析方法下两种统计方法的t 检验基本一致,但也只有单因素方差分析的讨论,缺乏双因素方差分析下回归模型的重构。



双因素方差的定义和使用条件
双因素方差分析(Two-way ANOVA)是一种统计方法,用于分析两个因
素对实验结果的影响。
该方法主要用来检验两个因子对因变量的交互作用。
双因素方差分析特别适用于那些同时受到两个或更多因素影响的因变量研究。
使用双因素方差分析时,需要满足以下条件:
1. 独立性:各个观测值之间必须相互独立,这意味着每个观测值都不受其他观测值的干扰。
2. 正态性:样本必须来自正态分布总体。
3. 方差齐性:各个总体的方差必须相等,即抽样的总体必须是等方差的。
4. 样本容量:每个组中的观测值数量应该足够多,这样才能保证估计的参数接近真实值。
5. 满足其他假设:例如,误差项应该是随机的,并且服从均值为0的正态分布。
双因素方差分析的步骤如下:
1. 提出假设:包括主效应和交互效应的假设。
2. 方差分析表:列出观测值的数量、各组的均值和方差以及总均值和总方差。
3. F检验:通过F检验来检验主效应和交互效应的显著性。
4. 结果解释:如果F检验的结果显著,则说明主效应或交互效应对因变量有影响;否则,说明没有影响。
以上信息仅供参考,如需获取更多详细信息,建议咨询统计学专家或查阅统计学相关书籍。
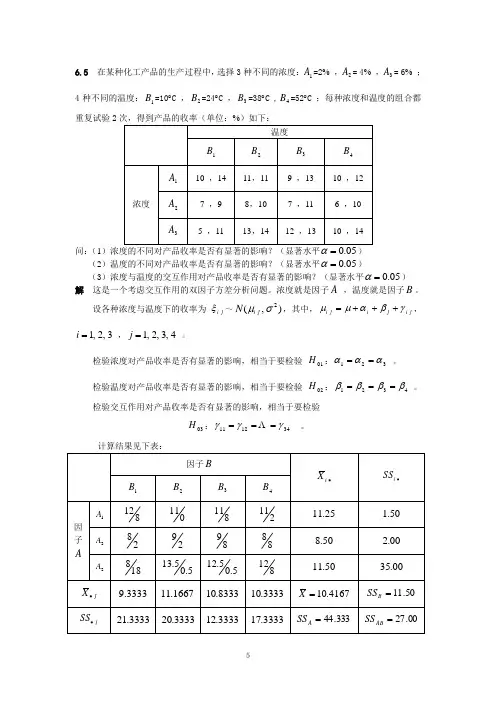
6.5 在某种化工产品的生产过程中,选择3种不同的浓度:1A =2% ,2A = 4% ,3A = 6% ;4种不同的温度:1B =10︒C ,2B =24︒C ,3B =38︒C ,4B =52︒C ;每种浓度和温度的组合都重复试验2问:(1)浓度的不同对产品收率是否有显著的影响?(显著水平) (2)温度的不同对产品收率是否有显著的影响?(显著水平05.0=α)(3)浓度与温度的交互作用对产品收率是否有显著的影响?(显著水平05.0=α) 解 这是一个考虑交互作用的双因子方差分析问题。
浓度就是因子A ,温度就是因子B 。
设各种浓度与温度下的收率为 j i ξ~),(2σμj i N ,其中,j i j i j i γβαμμ+++=,3,2,1=i ,4,3,2,1=j 。
检验浓度对产品收率是否有显著的影响,相当于要检验 01H :321ααα== 。
检验温度对产品收率是否有显著的影响,相当于要检验 02H :4321ββββ=== 。
检验交互作用对产品收率是否有显著的影响,相当于要检验03H :341211γγγ=== 。
计算结果见下表:06.7492.2588.282.1682.862.100.1811=+++++==∑∑==r i sj j i e SS SS 。
方差分析表为:因为 ))1(,1(89.309.41--=>=-t s r r F F A α,所以拒绝 01H , 浓度的不同对产品收率有显著的影响。
因为 ))1(,1(49.371.01--=<=-t s r s F F B α ,所以接受02H ,温度的不同对产品收率没有显著的影响。
因为 ))1(),1)(1((00.383.01---=<=-t s r s r F F AB α ,所以拒绝03H ,浓度与温度的交互作用对产品收率没有显著的影响。
6.6 某化工厂为了提高塑料大红R 颜料的收率,对合成过程中的酰氯化反应条件进行3因子3水平正交试验,所取的因子和水平分别为:因子 A 是酰氯化温度,1A 是85︒C ,2A 是95︒C ,3A 是105︒C ; 因子 B 是SOCl 2用量,1B 是4.2 ml ,2B 是4.6 ml ,3B 是5.0 ml ; 因子 C 是催化剂用量,1C 是0.2 ml ,2C 是0.5 ml ,3C 是0.8 ml 。





如何进行有交互多因方差分析
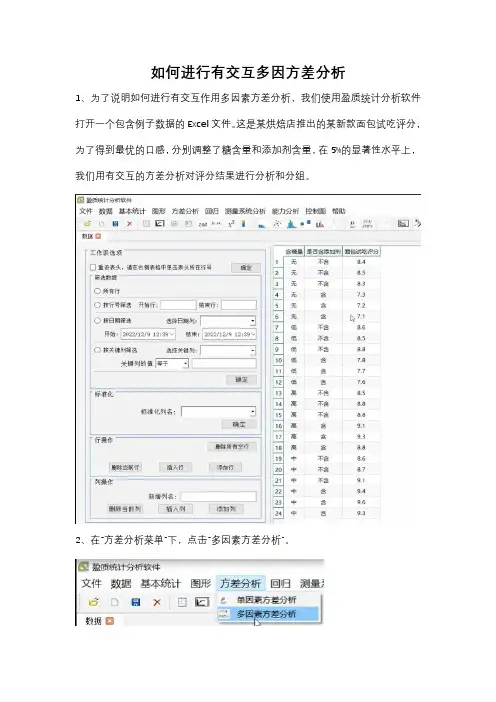
1、为了说明如何进行有交互作用多因素方差分析,我们使用盈质统计分析软件打开一个包含例子数据的Excel文件。
这是某烘焙店推出的某新款面包试吃评分,为了得到最优的口感,分别调整了糖含量和添加剂含量,在5%的显著性水平上,我们用有交互的方差分析对评分结果进行分析和分组。
2、在“方差分析菜单”下,点击“多因素方差分析”。
3、响应选择“面包试吃评分”,因子,单击“点击添加按钮”,选择“含糖量”、“是否含添加剂”,添加至右边,确认提交,勾选交互作用选项。
4、点击确定,会自动生成有交互作用的双因素方差分析结果和Tukey多重比较分组结果。
5、我们来看这个例子的分析结果,首先看因子信息,列出了两个因子的各个水平。
重点看方差分析表各个因子的P值,含糖量P值为0,小于显著性水平0.05,说明含糖量对面包的试吃评分有影响;是否含添加剂,P值为0.001,说明是否含添加剂对试吃评分也有影响;含糖量:是否含添加剂的P值为0,说明含糖量与是否含添加剂对面包试吃评分有交互作用的影响。
6、最后看通过Tukey方法给出的多重比较结果分组。
分别按因子进行了比较和
分组。
“含糖量”因子,“中”和“高”同属A组,“低”和“无”分属B和C组。
“是否含添加剂”因子,“不含”和“含”分属A和B组;重点看“含糖量”和“是否含添加剂”交互作用的分组,按评分由高至低排列,得到评分最高的A组为含糖量中等,且含有添加剂,所以,店家决定按这个配方制作该款面包,以得到最优口感。
7、如需查看完整视频或了解更多信息,请百度搜索“盈质统计分析软件”进行查看。
2、有交互影响的双因素方差分析假设两个因素A 和B ,因素A 有a 个水平,因素B 有b 个水平,对每一个水平A i B j重复了n 次试验。
X ijk 为在因素A 的第i 个水平,因素B 的第j 个水平下进行第k 次试验时的观察值(i =1,2... a ;j =1,2,...b ;k =1,2,...,n)。
有交互影响的双因素方差分析表如下:表9-12 有交互影响的双因素分析表其中:21()ai SSA bn i X A ==*∑-21()bj SSB na j X B==*-∑211(())ab i j SSAB n i jij X AB A B =-=--+∑∑2111()()abni j k SSE ijk ijA B X ====-⨯∑∑∑ 在显著性水平α下,如果F>临界值F α,则拒绝原假设,认为差异显著。
小案例9-2:不同路段和不同时间段对行车时间的影响城市道路交通管理部门为研究不同的路段和不同的时间段对行车时间的影响,让一名交通警察分别在两个路段和高峰期与非高峰期亲自驾车进行试验,通过试验共获得了20个行车时间的数据,如表9-13。
试分析路段、时段以及路段和时段的交互作用对行车时间的影响。
路段与时段对行车时间的影响:交互作用 无交互作用图9-1 有无交互作用的图示表9-13 不同的路段和不同的时间段对行车时间的影响数据表 (单位:min)路段(列变量)路段1路段2 时段(行变量)高 峰 期26 19 24 20 27 23 25 22 2521 非 高 峰 期20 18 17 17 22 13 21 16 1712通过计算,可以得到如表9-14所示的交互作用方差分析表。
可以得到:不同路段对行车时间有显著影响,不同时段对行车时间有显著影响,而路段与时段的交互作用对行车时间没有显著影响。
表9-14 交互作用方差分析表差异源 SS df MS F P 值 样本 174.0500 1 174.0500 44.0633 0.00000 列 92.4500 1 92.4500 23.4051 0.00002 交互 0.0500 1 0.0500 0.01270.9118内部 63.200 16 3.9500总计329.7519。
第九章双向方差分析
双向方差分析的基本原理是将观测值拆分为不同因素和交互作用的影响,并通过计算方差分析来判断因素和交互作用是否显著。
这种方法可以
帮助研究者确定不同因素对观测值的相对重要性,以及它们之间的相互关系。
双向方差分析有两个自变量和一个因变量。
第一个自变量称为行因素,第二个自变量称为列因素,因变量是我们想要比较的指标。
例如,我们可
以考察一个药物对不同性别和年龄组别的患者的疗效,并将性别和年龄分
别作为行因素和列因素,疗效作为因变量。
在进行双向方差分析之前,我们需要先进行数据收集和整理,确保数
据的完整性和合理性。
然后,我们可以通过计算方差分析表来检验不同因
素和交互作用的显著性。
双向方差分析的结果可以呈现在图形或表格中,以便更直观地理解和
比较不同因素和交互作用的影响。
例如,我们可以通过绘制柱状图来显示
不同因素和交互作用对观测值的平均影响,并通过误差线来表示平均值的
置信区间。
双向方差分析还可以用于比较多个因素和交互作用之间的差异。
例如,如果我们有一个实验涉及三个因素和它们之间的交互作用,我们可以使用
双向方差分析来比较这些因素和交互作用之间的差异,以确定哪些因素和
交互作用对观测值的影响最显著。
总之,双向方差分析是一种非常有用的统计方法,可以帮助研究者比
较和分析两个或多个因素对观测值的影响,并判断它们之间的交互作用是
否显著。
它不仅可以提供关于不同因素和交互作用的相对重要性的信息,还可以为进一步的研究和决策提供科学依据。