双因素方差分析法非常好的具体实例

格式：ppt
大小：1.11 MB
文档页数：33

下载文档原格式

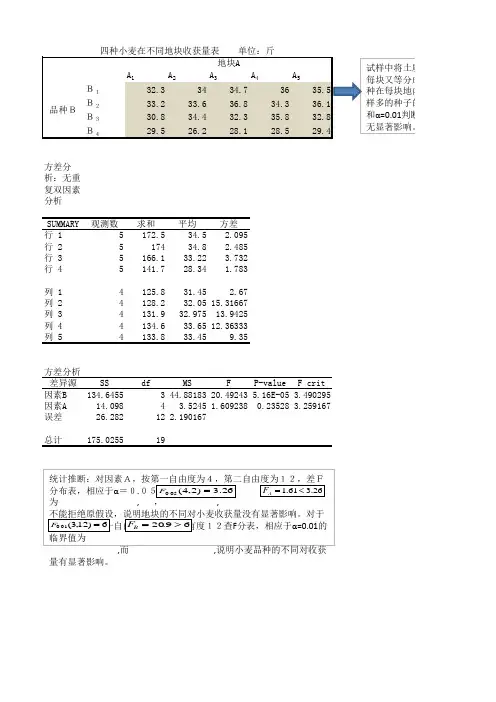
因子分析：双因子方差分析

方差分析：无重复双因素分析 SUMMARY 行 1 行 2 行 3 行 4 列列列列列 1 2 3 4 5 观测数 5 5 5 5 4 4 4 4 4 求和 172.5 174 166.1 141.7 125.8 128.2 131.9 134.6 133.8 平均 34.5 34.8 33.22 28.34 方差 2.095 2.485 3.732 1.783
31.45 2.67 32.05 15.31667 32.975 13.9425 33.65 12.36333 33.45 9.35
方差分析差异源 SS 因素B 134.6455 因素A 14.098 误差 26.282 总计 175.0255
df
MS F P-value F crit 3 44.88183 20.49243 5.16E-05 3.490295 4 3.5245 1.609238 0.235断：对因素Ａ，按第一自由度为４，第二自由度为１２，差Ｆ F0.05 ( 4,2) 3.26 FA 1.61 3.26 分布表，相应于α＝０.０５的临界值为 , ， , 不能拒绝原假设，说明地块的不同对小麦收获量没有显著影响。对于 F0.01(3,12) 6 F .9 6 B 20 因素Ｂ，按第一自由度３，第二自有度１２查 F分表，相应于α=0.01的临界值为 ,而 ,说明小麦品种的不同对收获量有显著影响。
四种小麦在不同地块收获量表单位：斤地块A A1 A2 A3 A4 Ｂ１Ｂ２品种ＢＢ３Ｂ４ 32.3 33.2 30.8 29.5 34 33.6 34.4 26.2 34.7 36.8 32.3 28.1 36 34.3 35.8 28.5
A5 35.5 36.1 32.8 29.4

论文—双因素试验的方差分析

X ijk ~ N (ij , 2 ) （ ij 和 2 未知），记 X ijk i = ijk ，即有
ijk X ij ijk ~ N (0, 2 ), 故 X ijk ijk 可视为随机误差. 从而得到如下数学模型
X ijk ij ijk， ijk ~ N（0， 2），各 ijk 相互独立， i 1, , r; j 1, , s; k 1, , t;
1 st
1 rt
X
j 1 k 1
r t
s
t
ijk
，i=1，2，，r，
X
j =
X
i 1 k 1
类似地，引入记号：， i , j , i , j , 易见

i 1
r
i 0 ，

j 1
s
j
0.
为水平 B j 的效应. 这样可以将
仍称为总平均，称 i 为水平 A i 的效应，称成
ij
j
ij
表示
= + i + j +
ij
（ i 1, , r; j 1, , s ），
(3)
与无重复试验的情况类似，此类问题的检验方法也是建立在偏差平方和的分解上的。 2. 偏差平方和及其分解引入记号： X =
1 rst
X
i 1 j 1 k 1
r
s
t
ijk
，
X
ij =
1 X ijk ，i=1，2，，r，j=1，2，，s， t k 1

t
X
i =
试验结因素果 A 因素 B

交互作用双因子方差分析

st
xijk
j1 k 1
称为水平 Ai 下的样本均值；
x• j•
1 rt
r i1
t
xijk
k 1
称为水平 B j 下的样本均值。
r s t
考虑总变差平方和 ST 2 xijk x 2 的如下分解：
i1 j1 k 1
r s t
ST 2
xijk x 2
i1 j1 k1 rst
若 H01 成立，即 1 2 r 0 ，那么，虽然不能苛求做为诸i 的估计值之平方和的若干倍的S A2
rst
r
（ xi•• x 2 st xi•• x 2 ）恰好等于零，
i1 j1 k 1
i 1
但相对于 SE
2
来说一定不应太大，倘若
SA2 SE2
超过某个界
限值k1 ，我们就有理由拒绝H01 ，故
0.
s
类似地，由 j
j 1
s j 1
u• j u
1 r
s j 1
r i 1
uij
su
0
r
r
r
ij uij ui• u• j u uij u• j ru• j ru• j 0
i 1
i 1
i 1
s
s
s
ij uij ui u• j u uij ui• sui• sui• 0
2
=
xijk xij• xi•• x x• j• x xij• xi•• x• j• x
i1 j 1 k 1
r s t
rst
rst
xijk xij• 2 xi•• x 2 x• j• x 2
i1 j1 k 1
i 1 j 1 k 1

双因素方差分析

双因素方差分析
在实际问题的研究中，有时需要考虑两个因素对实验结果的影响。

例如饮料销售，除了关心饮料颜色之外，我们还想了解销售地区是否影响销售量，如果在不同的地区，销售量存在显著的差异，就需要分析原因。

采用不同的销售策略，使该饮料品牌在市场占有率高的地区继续深入人心，保持领先地位；在市场占有率低的地区，进一步扩大宣传，让更多的消费者了解、接受该产品。

若把饮料的颜色看作影响销售量的因素A，饮料的销售地区则是影响因素B。

对因素A和因素B 同时进行分析，就属于双因素方差分析的内容，双因素方差分析是对影响因素进行检验，究竟是一个因素在起作用，还是两个因素都起作用，或是两个因素的影响都不显著。

双因素方差分析有两种类型：一个是无交互作用的双因素方差分析，它假定因素A和因素B的效应之间是相互独立的，不存在相互关系；另一个是有交互作用的双因素方差分析，它假定因素A和因素B 的结合会产生出一种新的效应。

例如，若假定不同地区的消费者对某种颜色有与其他地区消费者不同的特殊偏爱，这就是两个因素结合后产生的新效应，属于有交互作用的背景；否则，就是无交互作用的背景。

有交互作用的双因素方差分析已超出本书的范围，这里介绍无交互作用的双因素方差分析。

21两因素有重复方差分析-PPT文档资料32页

11
方差分析表
行间列间交互误差
SS 315.83 207.17
50.33 55.00
df MS 2 157.92 4 51.79 8 6.29
45 1.22
F
F0.05
129.21 **
42.38 **
5.15 **
F0.01 5.12 3.77 2.93
总变异 628.33 59
安康学院
12
安康学院
21
方差分析表
一级间A 二级间B 误差e
SS df
81.47
4
79.32 10
21.33 30
MS
20.368 7.932 0.711
F F0.05 F0.01 28.64** 2.69 4.02 11.16** 2.16 2.98
总变异 182.13 44
安康学院
22
多重比较（一级因素）
b
B
A3
75.67
b
B
安康学院
7
列间多重比较 (SSR 法) 临界值表
dfe 秩次距 k SSR 0.05 SSR 0.01 LSR0.05 LSR0.01
27
2
2.91 3.93 9.28 12.54
取26 3
3.06 4.11 9.76 13.11
行(A 间 )sxa
MeS bn
12 .324 3.19 34
安康学院
17
观测值数据表
一级二级
n1
n2
n3 二级平均一级平均
A1
B1
15.6
16.4
15.6
15.9
B2
13.6
15.6

方差分析实例详解

方差分析计算实例一、单因素方差分析二、双因素方差分析一、单因素方差分析（一）完全随机试验设计1、重复数相同（1）实例：不同浇水量对某蔬菜产量的影响试验，设置5个浇水量A、B、C、D、E；每个浇水量设置四个小区，小区采用完全随机试验设计；各小区产量见下表（单位：kg）（2）基本参数计算处理数k=5，重复数n=4220.0250.9750.485,11.143χχ==（3）方差同质性检验2220.0250.975,c χχχ≤≤五个处理的方差无显著差异平方和计算：（4）方差分析自由度计算：方差分析表：22222222/()/()(45.2869.5288.55108.48130.12)/4441.95/(45)1089.89t i ij SS T n x nk =−=++++−⨯=∑∑1107.051089.8917.16e T t SS SS SS =−=−=222222()/()16.6115.9531.11441.95/(45)1107.05T ijij SS x x nk =−=+++−⨯=∑∑1514t df k =−=−=(1)5(41)15e df k n =−=−=145119T df nk =−=⨯−=变异来源平方和自由度均方F 值F 0.05处理间1089.894272.47238.213.056误差17.1615 1.14总变异1107.0519F 值大于F 0.05，五个处理蔬菜产量平均值差异显著。

将五个处理小区产量平均值从大到小排列，采用字母标记法表示各均值间差异是否显著，均值间的差值大于LSD ，差异显著，标记不同的字母；均值间的差值小于LSD ，差异不显著，标记相同的字母。

标记字母时，第一个值标a ，用最大值减第二个值，差值若大于LSD 则标b ，差值若小于LSD 则标a ，再以最大值减第三个值，直到出现大于LSD 值，标记b ，再以该值为标准向上比较，若差值大于LSD 就停止比较，若小于LSD 值则在a 后面加上b ，直至出现差值大于LSD 就停止比较；再以最上面标记b 的均值为标准在向下比较；直到所有的平均值都标记字母。

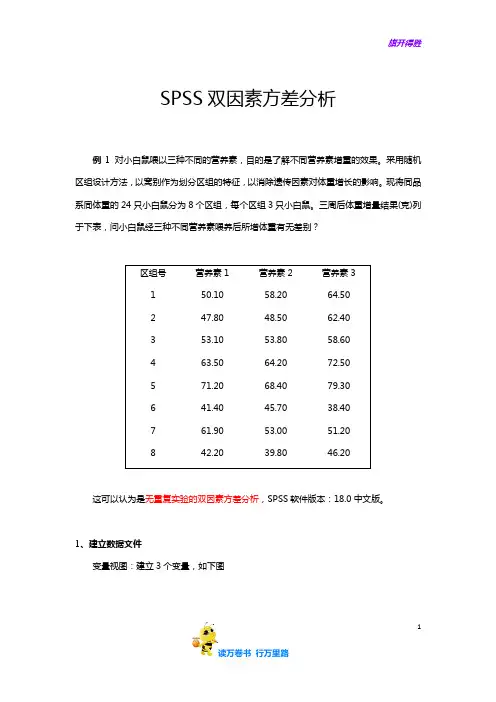
SPSS双因素方差分析

SPSS双因素方差分析例1 对小白鼠喂以三种不同的营养素，目的是了解不同营养素增重的效果。

采用随机区组设计方法，以窝别作为划分区组的特征，以消除遗传因素对体重增长的影响。

现将同品系同体重的24只小白鼠分为8个区组，每个区组3只小白鼠。

三周后体重增量结果(克)列于下表，问小白鼠经三种不同营养素喂养后所增体重有无差别？区组号营养素1 营养素2 营养素31 50.10 58.20 64.502 47.80 48.50 62.403 53.10 53.80 58.604 63.50 64.20 72.505 71.20 68.40 79.306 41.40 45.70 38.407 61.90 53.00 51.208 42.20 39.80 46.20这可以认为是无重复实验的双因素方差分析，SPSS软件版本：18.0中文版。

1、建立数据文件变量视图：建立3个变量，如下图1数据视图：如下图：区组号用1-8表示，营养素号用1-3表示。

数据文件见“小白鼠喂3种不同的营养素增重数量.sav”，可以直接使用。

2、统计分析菜单选择：分析-> 一般线性模型-> 单变量1点击进入“单变量”对话框1旗开得胜将“体重”选入“因变量”框，“区组”、“营养素”选入固定因子框点击右边“模型”按钮，进入“单变量：模型对话框”1点击“设定”单选按钮（无重复双因素方差分析不能选全因子！），在“构建项”下拉菜单中选择“主效应”（只能选主效应）1把左边的因子与协变量框中区组和营养素均选入右边的模型框中其余选项取默认值就行，点击“继续”按钮，回到“单变量”界面1点击“两两比较”按钮，进入下面对话框1将左边框中“区组”、“营养素”均选入右边框中再选择两两比较的方法，LSD、S-N-K，Duncan为常用的三种方法，点击“继续”按钮回到“单变量”主界面。

1点击“选项”按钮1勾选“统计描述”及“方差齐性检验”，设置显著性水平，点击“继续”按钮，回到“单变量”主界面1点击下方“确定”按钮，开始分析。

Minib两因素方差分析

注意：设立区组的目的，就是把区组平方和从总平方和分解出来，
免其对处理平方和与误差平方和的干扰，从而加强以后判断
的准确性．
各平方和的简化计算公式
Minitab
ST
v i 1
b
yi2j
j 1
T2 , vb
fT vb-1
SA
T12
T22
Tv2 b
T2 , vb
f A v-1
SB
B12
B22 Bb2 v
其中
yij －第 i 个处理在第 j 个区组内的观察值．
－总均值．
ai －第 i 个固定处理的效应，且满足 a1 a2 av 0 ．
b
j
－第
j
个随机区组的效应，诸
b
j
是来正态分布
N
(0,
2 b
)
的一个样本，其中
2 b
是区组效应的方差分量．
ij －试验误差， ij ~ N (0, 2 ) ，诸 ij 与诸 b j 相互独立， 2
F
MS A MS e
SA Se
/ /
fA fe
~
F( fA,
fe )
•等价于检验如下一对假设：
H0：a1 a2 av 0 H1：诸ai中至少有一个不为零在此假设下，检验统计量为
F MS A MSe
Minitab
随机化完全区组设计的方差分析表
随机化完全区组设计的方差分析表
来平方和
源
E(SA ) (v 1) 2 b ai2
i 1
E(SB
)
(b
1)
2
v(b
1)
2 b
E(Se ) (v 1)(b 1) 2

8.9有交互作用双因素方差分析问题描述

r
mij
j =1
=1 k
k
1
i=1 mi鬃= r
r
mj
j =1
å1 r
mi× = r
mij
j =1
å m×j
=
1 k
k i =1
mij
ai = mi× - m
bj = m×j - m
i =1, 2,..., k
j =1, 2,..., r i =1, 2,..., k j =1, 2,..., r
(ab)ij = mij - mi鬃- m j + m
ì ï
X ij
= mij
+ ai
+bj
+ (ab)ij
+e ijs
ï ïï
e ijs
~
N (0,s
2 ), 各e ijs独立
í ï
i
=1, 2,..., k;
j
=1, 2,..., r; s
=1, 2,..., t
邋邋 ï k
r
k
r
ï ïî
ai
i =1
= 0; bj
i =1
= 0; (ab)ij
i =1
… ..., X krt
… T鬃r
… X 鬃r
…
Ti鬃
X i鬃
…
…
Tk鬃
X k鬃
总和总均值
TX
有交互作用双因素方差分析问题描述
所考察的因素记为
因素共有个水平因素共有个水平
Xijs ~ N(mij ,s 2)(i =1, 2,..., k; j =1, 2,..., r; s =1, 2,...,t) 其中，

双因素方差分析在地球化学数据处理中的应用

双因素方差分析在地球化学数据处理中的应用
李昱星（长安大学地球科学与资源学院陕西西安
７１００５４）
Ｅｘｃｅபைடு நூலகம்ｌ，ｓｐｓｓ和ｍａｌｆａｂ都可以实现双凶素方差分析，在实验中发现ｓｐｓｓ较为简单易用，下面演示ｓｐｓｓ如何进行处理。首先要对给定的数据在ＥＸＣＥＬ中进行处理，处理为如表２
Ｙｕ＝Ｍ＋ＤＩ＋＋１３
源
表３
其中Ｙｕ为在岩性为Ｉ，深度为Ｊ的土壤中取得的地球化学样中金属ｃｕ的含量，Ｍ为样品中ｃｕ含量的平均值，ＤＩ为由于岩性引起的ｃｕ含量的异常，Ｌ为由于样品取样深度引起的ｃｕ含量的异常。１３为由于随机【大ｊ素导致的异常。但是以上双因素的模型并不严谨，因为可能出现如下状况：图表参数解释：Ｓ＝１０２２．８９６，Ｓ＝０．１，Ｓ＋＝０．３９６，Ｓ比如深度是否能够体现出异常要看岩性具体是什么类型；或者岩４．２３６；ＤＦ为个素自南度，其中岩性，深度为２，岩性深度性是否能体现出异常，要看具体的取样深度而定。这种状况被称为４，误差为３６，均方为个素条件误差值昱其自Ｆｆ｝度的比值。Ｆ为两个因素存在交互作用，此时需要在模型中加入交互项。为各要素统计量。Ｙｕ＝Ｍ＋ＤＩ＋ＬＪ＋Ｂ＋ｉｊＳＩＧ值为湿著性检验值：这里的表现的是岩性为Ｊ，深度为ｉ时两者的交互作用。岩性的ＳＩＧ值＜０．０５，所以在０．０５的著水平上认为其方筹在数学建模时未考虑每组合的多次取样，可以比较清楚的建是显著的，即岩性不同的情况下土壤中ｃｕ的含量变化很大，深度立较为简单易懂的模型。以及深度岩性的ＳＩＧ＞Ｏ．０５，所以在０．０５的显著性水平上认为其ＩＩ对模型中效应的检验：方差无显著差异，故对ｃｕ的含量多少没有影响。由于岩性对ｃｕ建立好模型后，要对岩性和深度这两个凶素对ｃｕ含量的作含量的显著性影响，故在做地球化学数据处理的过程中需要对不用进行检验，根据上面模型的公式，可以将总的样本离均差的和同岩性的岩石选取不同的地球化学背景值。分解成几部分：ＳＳ＝ＳＳ＋ＳＳＤ＋ＳＳ误，然后用每个离均差参考文献平方和除以自由度就可以得到均方，例如：Ｍｓ：ＳＳ／１）Ｆ，［１］ＧｅｏｒｅｇｅＳ．ｋｏｃｈ，ＪｒＲｉｃｈａｒｄＦ．Ｌｉｎｋ．１９７０，ＳＴＡＴＩＳＴＩＣＡ１ＡＮＡＬ — 最后将各效应的均方与误差的均方相比较就得到了Ｆ统计量，例ＹＳＩＳＯＦＧＥＯＬＯＧＩＣＡＬＤＡＴＡ，ｊｏｈｎｗｉｌｅｙ＆ｓｏｎｓ，ｉｎｃ如Ｆ岩性＝ＭＳ／ＭＳ。借助Ｆ分布，就可以知道岩性和深度对【２］杨永同．数学地质［Ｍ］．徐州：中国矿业大学出版社，２０１０Ｃｕ的含量有多大的影响。［３】吴锡生．化探数据处理方法【Ｍ１．北京：地质出版社，１９９３

双因素方差分析法非常好的具体实例课件

数据预处理与筛选
02
01
03
对原始数据进行清理和筛选，处理缺失值和异常值，确保数据质量。
对分类变量进行适当的编码和转换，使其符合分析要求。
对连续变量进行适当的变换，如对数转换或标准化处理，以满足正态分布和方差齐性的假设。
结果解读与报告撰写
仔细解读双因素方差分析的结果，包括F值、P值、效应大小和方向等。
混合类型数据
对于同时包含分类和数值型变量的数据，如何进行有效的双因素方差分析是一个值得研究的问题。
THANK YOU
感谢聆听
结合实际问题和专业知识，对结果进行解释和讨论，并给出合理的结论和建议。
按照学术规范撰写报告，注意逻辑性和条理性，并适当使用图表和表格来呈现结果。
04
双因素方差分析法的未来发展与展望
技术创新与改进
算法优化
随着计算能力的提升，双因素方差分析算法将进一步优化，提高分析的准确性和效率。
自动化程度提高
特点
能够同时考虑两个因素对连续变量的影响，并比较各组之间的差异。
适用范围
当有两个分类变量，且需要探讨它们对一个连续变量的影响时。
适用于探索两个因素对连续变量的交互作用和主效应。
优势与局限性
优势
能够全面分析两个因素对连续变量的影响，并提供交互作用和主效应的估计。
局限性
当样本量较小或数据不满足方差分析的前提假设时，分析结果可能不准确。
未来分析过程可能更加自动化，减少人工干预，降低错误率。
可视化呈现
数据分析结果将以更直观的方式呈现，方便用户理解和解释。
应用领域的拓展
80%
跨学科应用
双因素方差分析法将应用于更多学科领域，促进不同学科之间的交叉融合。

统计学双因素方差分析论文

关于林业部门对松树的不同树种在不同地区的生长情况的数据分析—---———统计学双因素方差分析摘要：松树，又名常青树，顾名思义它四季都是绿色的，使人们四季都能有春天的感觉.它不仅有很高的观赏价值，还很坚固顽强，常年不死。

因此如果在城市种植的话，不但可以供市民观赏，而且它的存活机率高，便于林业部门打理。

但它的种类繁多，而且不同地区的土壤也是有差别的，林业部门想根据其生长的直径,考虑不同的树种和不同的地区对它的生长状况有怎样的影响.采用双因素方差分析方法.关键词：双因素方差分析直径 SPSS软件正文：一、引文:松树，又名常青树,顾名思义它四季都是绿色的，使人们四季都能有春天的感觉。

它不仅有很高的观赏价值，还很坚固顽强，常年不死。

但它的种类繁多，而且不同地区的土壤也是有差别的，林业部门想根据其生长的直径，考虑不同的树种和不同的地区对它的生长状况有怎样的影响。

采取的分析方法：有重复双因素方差分析，单因素方差分析.分析过程应用了Excel 2003 软件和 SPSS 统计学软件。

二、统计学分析方法的理论依据：方差分析（ANOVA）是通过检验各总体均值是否相等来判断分类型数据自变量对数值型因变量是否有显著影响。

双因素方差分析法是一种统计分析方法，这种分析方法可以用来分析两个因素的不同水平对结果是否有显著影响,以及两因素之间是否存在交互效应。

因为在实际应用中，一个试验结果(试验指标）往往受多个因素的影响。

不仅这些因素会影响试验结果，而且这些因素的不同水平的搭配也会影响试验结果。

一般运用双因素方差分析法，先对两个因素的不同水平的组合进行设计试验，要求每个组合下所得到的样本的含量都是相同的。

在本分析中，我们所研究的因素是地区和松树种类，水平是不同的地区和不同的松树。

本分析中使用的有重复双因素方差分析方法即有交互作用的双因素方差分析方法。

有交互作用的双因素方差分析处理方法：把交互作用当成一个新因素来处理，即把每种搭配A i B j 看作一个总体X ij 。

16双因素方差分析

一、模型条件
正态性：各样本来自正态分布
方差齐性：各样处理组总体方差齐；各区组总体方差齐。
12
处理组间正态性检验结果
13
区组间正态性检验结果
14
处理组的残差诊断——方差齐性
15
区组的残差诊断——方差齐性
16
二、基本思想
SS组内
SS总
变异之间的关系：
SS组间
SS配伍
• SS总= SS组内+ SS组间+ SS配伍间
方差分析结果
SS
12.6147 3.0527 5.5280 4.0340

29 2 9 18
MS
1.5264 0.6142 0.2241
F
6.8112 2.7407
P
0.0063 0.0328
3 确定 P值，作出推断结论查 F界值表得：不同处理组的 P<0.05，所以认为A、B、C三种方案的处理效果不全相同。不同区组 P<0.05，认为10个区组的总体均数不全相同。
33
34
总=
组内+ 组间+配伍间
17
三、基本步骤
配伍组设计资料的方差分析的
无效假设有二个，其一是关于处理
因素的，另一个是关于配伍因素的。相应的统计量也有二个。
1
建立检验假设，确定检验水准对于处理组 H0：三个总体均数全相等 H1：三个总体均数不全相等对于区组 H0 ：十个总体均数全相等 H1 ：十个总体均数不全相等 a=0.05
生物蛋白 4.3 4.1 3.5 4.8 5.1 3.3 3.1 4.2 3.8 4.8 4.1
X i
3.60 3.87 3.17 4.43 4.27 3.50 3.03 3.83 3.70 4.13 3.75( X )

双因素无重复试验方差分析

r 1
均方
MSA SA r 1
SB s 1
F
值
MSA MSE
MSB M Se
显著性
FA
SB QB P
s 1
MSB
FB
Se R QA QB P
ST R P
( r 1)( s 1) M S e
rs 1
Se ( r 1)( s 1)
2
均为未知参数

.
称为总平均
a i 称为水平 A i 的效应
b j 称为水平 A j 的效应
显然，
i 1
r
ai 0, b j 0
j 1
s
并且， ij 可表示为
ij a i b j
双因素无重复试验方差分析的数学模型
X ij ai b j ij , 2 ij～N (0, ), 各 ij 独立, i 1, 2, , r , j 1, 2,, s, r s ai 0, b j 0. i 1 j 1
任务：检验假设
H 0 1 : a1 a 2 a r 0 , H 1 1 : a1 , a 2 , , a r 不全为零 .
H 0 2 : b1 b 2 b s 0, H 1 2 : b1 , b 2 , , b s 不全为零 .

Bs
x1 1 x 21

x1 2
x 22

x1 s
x2s

Ar
x r1
xr 2

x rs
假设
X ij ～ N ( ij , ), i 1 , , r , j 1 , , s .

SPSS双因素实验处理实例

【例6.6】为了研究饲料中钙磷含量对幼猪生长发育的影响，将钙(A)、磷(B)在饲料中的含量各分4个水平进行交叉分组试验。

选用品种、性别、日龄相同，初始体重基本一致的幼猪48 头，随机分成16组，每组3头，用能量、蛋白质含量相同的饲料在不同钙磷用量搭配下各喂一组猪，经两月试验，幼猪增重结果(kg)列于表6-29，试分析钙磷对幼猪生长发育的影响。

本例A因素─钙的含量分4个水平，即a=4；B因素─磷的含量分4个水平，即b=4；共有ab=4×4=16个水平组合；每个水平组合重复数n=3；全试验共有=4×4×3=48个观测值。

表6-29不同钙磷用量(%)的试验猪增重结果(kg)1、计算各项平方和与自由度4919.36680)344/(9.1326/22...=⨯⨯==abnx C 3181.9824919.366808100.376624919.36680)0.190.205.260.22(22222=-=-++++=-=∑∑∑ C x SS ijl T 9048.8344919.366803967.375154919.36680)5.575.839.72(3112222.=-=-+++=-=∑ C x n SS ij AB7356.3834919.366802275.370644919.36680)1.2788.3578.3632.327(34115106.444919.366800025.367254919.36680)5.3194.3321.3509.324(341122222..22222..=-=-+++⨯=-==-=-+++⨯=-=∑∑C x an SS C x bnSS j B i A6586.4067356.3835106.449048.834=--=--=⨯BA AB B A SS SS SS SS 15144147134414133.1479048.8343181.982=-⨯=-==-⨯⨯=-==-=-=ab df abn df SS SS SS AB T AB T e 32)13(44)1(9)14)(14()1)(1(31413141=-⨯=-==--=--==-=-==-=-=⨯n ab df b a df b df a df e B A B A2、列出方差分析表，进行F检验表6-30 不同钙磷用量方差分析表查临界F 值：F 0.05(3,32)=2.90，F 0.01(3,32)=4.47；F 0.01(9,32)=3.02。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a b
2
SST
X ij X
i1 j 1
可分解为：SST SSA SSB SSE
a
2
SSA b X i. X
i 1
b
2
SSB a X . j X
j 1
称为因素A的离差平方和，反映因素 A 对试验指标的影响。
称为因素B的离差平方和，反映因素 B 对试验指标的影响。
a b
X ij
i 1
i1 j 1
X. j T. j a X .1 X .2 ... X .b
X 1T ab
➢ 无交互作用的双因素试验的方差分析
基本假设（1）X ij 相互独立；
（2）Xij ~ N ij , 2 ，（方差齐性）。
线性统计模型 X ij i j ij
其中
1 ab
a i 1
F0.01 3,6 9.78 F0.05 3,6 4.76 F0.01 2,6 10.92
FB F0.01 2,6
结论：工人对产品的产量有显著影响，机器对产品的产量有极显著影响。
例1的上机操作
原始数据，行因素水平，列因素水平
对应例1 的数据输入方式
工人对产品产量有显著影响，而机器对产品产量的影响极显著。
F 右侧检验
双因素（无交互作用）试验的方差分析表
方差来源平方和自由度均方和
因素A 因素B 误差总和
SS A SSB SSE SST
df A
MS A
SS A df A
df B
MSB
SSB df B
df E
MSE
SSE df E
dfT
F值
FA
MS A MSE
FB
MSB MSE
F 值临介值
F ( a 1 , a 1 b 1) F (b 1 , a 1 b 1)
若“各因素、各水平及其交互作用的影响无统计意义”的假设
成立，则 Xijk ~ N , 2
可推得： SSA
2
~
2 a 1,
SSB
2
~
2 b 1,
SST
2
~ 2 abn 1
SS AB
2
~
2 a bn 1
则
FA
SS A SSE
df A df E
MSA ~ F MSE
注意
df E
dfT
df A
fB,
SSE SST SSA SSB
各因素离差平方和的自由度为水平数减一，总平方
和的自由度为试验总次数减一。
双因素（无交互作用）试验的方差分析表
简便计算式：
SSA DA p, SSB DB p
SSE R DA DB p, SST R p
其中： DA
a
Ti.2
b,
i1
p T 2 ab ,
DB
b
T.
2 j
a,
j1
ab
R
X
2 ij
i1 j1
例1 设甲、乙、丙、丁四个工人操作机器Ⅰ、Ⅱ、Ⅲ各一天，其产品产量如下表，问工人和机器对产品产量是否有显著影响？
机器 B 工人 A
ⅠⅡ
Ⅲ
甲
50 63 52
乙
47 54 42
丙
47 57 41
b
ij
j 1
所有期望值的总平均
i
1 a
b
ij
j 1
ig
水平Ai对试验结果的效应
j
1 b
a i 1
ij
gj
水平Bj对试验结果的效应
ij X ij ij
试验误差
i
1 a
b
ij
j 1
ig
水平Ai对试验结果的效应
j
1 b
a i 1
ij
gj
水平Bj对试验结果的效应
ij X ij ij
双因素无重复（无交互作用）试验资料表
因素 B 因素 A
B1
b
B2 ... Bb Ti. X ij X i. Ti. b j 1
A1
X11 X12 ... X1b
T1.
X 1.
...
... ... ... ... ...
...
Aa
X a1 X a2 ... X ab
Ta.
X a.
a
ab
T. j Xij T.1 T.2 ... T.b T
2
SSE
X ij X i. X . j X
i1 j1
称为误差平方和，反映试验误差对试验指标的影响。
若假设 H01, H02成立，则： Xij ~ N , 2
可推得：
SST
2
~ 2 ab 1
SSA
2
~
2 a 1
SSB
2
~
2 b 1
SSE
2
~
2 a 1b 1
将
SST
2
,
SS A
2
,
a b n
2
SST
X ijk X
i1 j1 k 1
可分解为： SST SSA SSB SSAB SSE
SSA称为因素A的离差平方和，反映因素 A 对试验指标的影响。 SSB称为因素B的离差平方和，反映因素 B 对试验指标的影响。SSAB称为交互作用的离差平方和，反映交互作用AB对试验指标的影响。SSE称为误差平方和，反映试验误差对试验指标的影响。
各因素，各水平，各交互作用下的均值。
作业 P195 3 4（借助软件完成）
预习第三节正交试验设计及其统计分析
R
X
2 ij
31678
i1 j1
DA
1 b
a
Ti.2
i 1
23495
DB
1 a
b
T.
2 j
j 1
42040.67
p T 2 31212 ab
SST R p 466
dfT n 1 11
SSA DA p 114.67
dfA a 1 3
SSB DB p 318.5
dfB b 1 2
SSE SST SSA SSB 32.83 dfE dfA dfb 6
MSA SSA dfA 38.223
MSB SSB dfB 159.25
MSE SSE dfE 5.47 FA MSA MSE 6.98 FB MSB MSE 29.10
F0.05 3,6 FA F0.01 3,6
~ F a 1, a 1b 1
FB
SSB SSE
df B df E
MSB MSE
~ F b 1, a 1b 1
对给定的检验水平，
当 FA F a 1, a 1b 1 时，
拒绝H01，即A 因素的影响有统计意义。
当 FB F b 1, a 1b 1 时，
拒绝H02，即B 因素的影响有统计意义。
因素 B 因素 A
B1
X111
A1
...
X11n
...
B2
...
Bb
X121
...
X1b1
...
...
...
X12n
...
X1bn
......
X a11
X a21
...
X ab1
Aa
...
...
...
...
X a1n
X a2n
...
X abn
双因素（有重复）试验方差分析表
方差来源平方和自由度均方和
其中
1 ab
a i 1
b
ij
j 1
所有期望值的总平均
i
1 a
b
ij
j 1
ig
水平Ai对试验结果的效应
j
1 b
a i 1
ij
gj
水平Bj对试验结果的效应
ij
ij
i
j
交互效应
ijk X ijk ij 试验误差
a
b
特性： i 0; j 0;
i 1
j 1
a
b
ij 0; ij 0; ijk ~ N 0, 2
B2
6.15 7.86 7.38 7.05 6.30 5.81 6.54 6.63
B3
4.93 5.59 6.10 5.46 3.33 2.85 3.60 3.19
输入数据时，C2表示行因素水平，C3表示列因素水平。第几次重复不必列明，软件
自会识别。
结果显示如P185
均<0.01
饲料中能量的高低、蛋白质含量的不同及两者的交互作用对鱼的体重的影响极有统计意义。
基本假设（1）X ij 相互独立；
（2）Xij ~ N ij , 2 ，（方差齐性）。
线性统计模型
因素B
总平均的效应
试验误差
Xijk i j ij ijk
观测值
因素A
交互作用
的效应的效应
➢ 有交互作用的双因素试验的方差分析
线性统计模型 Xijk i j ij ijk
试验误差
a
b
特性： i 0; j 0; ij ~ N 0, 2
i 1
j 1
要分析因素A，B的差异对试验结果是否有显著
影响，即为检验如下假设是否成立：
H01 :1 2 L a 0 H02 : 1 2 L b 0
➢ 总离差平方和的分解定理
仿单因素方差分析的方法，考察总离差平方和
丁
53 58 48
a
T. j Xij i 1
197 232 183
b
Ti. X ij j 1 165 143 145 159