当前位置：文档之家 › 典型环节的传递函数

典型环节的传递函数

  • 格式：pdf
  • 大小：420.27 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

典型环节传递函数

典型环节传递函数
θ 1 θ 2
u(t ) K1[1 (t ) 2 (t )] K1 (t )
K1 2 K11 图2-9 电位器
U(t)
K1是单个电位器的传递函数， (t ) 1 (t ) 2 (t ) 是两个电位器电刷角位移之差，称误差角。
U (s) K1 ( s )
5 振荡环节
n 1 G( s) 2 2 2 2 T S 2TS 1 S 2 n S n
2
T
1
式中 ξ－阻尼比 , (0 1) n -自然振荡角频率（无阻尼振荡角频率）
n
振荡环节的单位阶跃响应曲线
特点：环节中有两个独立的储能元件，并可进行能量交换，其
电位器的负载效应一般要求rl17测速发电机测量角速度并将它转换成电压量的装置直流测速发电机交流测速发电机dt图210测速发电机转子角速度radsktktsk18电枢控制直流伺服电动机例29中求得电枢控制直流电动机简化后的微分方程为tmk2tmk1tmk1stm图212两相伺服电动机两相定子线圈和一个高电阻值的转子组成
（b)
(t ) 转子角速度（rad/s）
Kt
Ω (s)
H (s)
Kt SKt 图2-11
U(s)
输出斜率（v/rad/s）
U ( s) Kt S ( s)
U(s)
G( s)
G( s)
U ( s) Kt ( )
18
电枢控制直流伺服电动机 例2-9中求得电枢控制直流电动机简化后的微分方程为
G (s) C (s) R( s)
如果将
S
d dt
置换 传递函数 微分方程
8
性质7
传递函数G(s)的拉氏反变换是脉冲响应g(t) 脉冲响应（脉冲过渡函数）g(t)是系统在单位脉冲输 入时的输出响应。

大学自动控制原理2.4典型环节传递函数

大学自动控制原理2.4典型环节传递函数
02
传递函数的零点和极点决定了系统的动态特性和稳定性。
03
传递函数的分子和分母多项式决定了系统的频率响应特性。
典型环节的分类
比例环节
输出信号与输入信号成正比，传递函 数为 G(s) = K，其中 K 为常数。
02
积分环节
输出信号与输入信号的时间积分成正 比，传递函数为 G(s) = 1 / (sT)，其 中 T 为时间常数。
将介绍控制系统的稳定性 分析方法。
掌握频率响应法在控制系 统设计中的应用。
学习如何利用根轨迹法进 行系统性能分析。
了解现代控制系统的基本 概念和分类。
THANKS FOR WATCHING
感谢您的观看
高阶环节的传递函数具有多个极点和零点，这些极点和零点 决定了环节的动态特性，如响应速度、超调和调节时间等。
实例分析
以一个三阶惯性环节为例，其传递函数为 $G(s) = frac{1}{s^3 + 2s^2 + 3s + 1}$，该环节具有三个极点 $s = -1, -1, -1$ 和一个 零点 $s = 0$。
拉普拉斯变换中的频率。
该传递函数是一个有理分式，分 母为线性多项式，分子为常数。
当输入信号 (s) 变化时，输出信 号 (G(s)) 会根据增益 (K) 和时间
常数 (T) 进行相应的变化。
实例分析
实例1
一阶惯性环节在电机控制系统中的应用，用于描述电机的动态响应特性。
实例2
在温度控制系统中的一阶惯性环节，用于描述加热元件的热量传递和散热过程。
04 一阶惯环节
定义与特点
定义
一阶惯性环节的传递函数为 (G(s) = frac{K}{T s + 1})，其中 (K) 是增益，(T) 是时间常 数。

5--典型环节传递函数-一阶惯性环节

5--典型环节传递函数-一阶惯性环节
)
一个储能元件(如电感、电容和弹簧等)和一个耗能元件(如 电阻、阻尼器等)的组合，就能构成一个惯性环节 当输入量发生突变时，输出量不能突变，只能按指数规 律逐渐变化，这就反映了该环节具有惯性。
1．微分方程
式中的 T为惯性时间常数。
一阶惯性环节（Ineritial Element)
2．传递函数与功能框
惯性环节的 功能框图
阶跃响应
一阶惯性环节（Ineritial Element)
3．动态
反变换：
一阶惯性环节（Ineritial Element)
4．举例 【实例1】电阻、电感电路，如 图所示。
由基尔霍夫定律可得电路
对上式进行拉氏变换,并整 理后可得：

2-4 典型环节及其传递函数

2-4 典型环节及其传递函数
1
气阻的数学表达式为 ∆p = R∆q ∆p 式中， 是气体压力降 ； ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ； R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) （３）喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 １，背压室 ２，喷嘴 ３，和挡板 ４ 组成，如图 ２－１８ 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时，可把喷嘴 1 2 4 一挡板机构看作一个比例环节，即 3 D ∆p D = k 1 ∆h 式中， 是喷嘴背压的变化； ∆p D ∆h 是挡板开度变化量； 是比例系数。 k1 d （４）放大器 h 在自动控制系统中用得最多的是运算放大 器，它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成，其符号如图 ２－ 3 − 喷嘴 4 − 挡板 １９ 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端，输出电压为 u 0 (t ) 它有两个输入端，一个是同相输入端 ｂ 用 “十”表示，一个是反相输入端 ａ 用“一”表示。当 放大器工作在放大区而不是饱和区时，输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中， 为开环放大倍数，这个数值很高，可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点： ①由于开环输入电阻很高，运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高，所以 ｂ 端和 Ｃ 端电位接近相等，即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节，但可用它来组成其他各种基本环节。

5-典型环节传递函数-振荡环节

5-典型环节传递函数-振荡环节
振荡环节(Oscillating Element)
2．传递函数与功能框
振荡环节的 功能框图阶跃响应振荡环节(Oscillating Element)
3．动态
当ξ=0时，c(t)为等幅自由振荡(又称为无阻尼振荡)。 其振荡频率为ωn，ωn称为无阻尼自然振荡 频率。
当0<ξ<1时，c(t)为减幅振荡(又称为阻尼振荡)。其振 荡频率为ωd, ωd称为阻尼自然振荡频率。
振荡环节(Oscillating Element)
4．举例
【实例1】 图为一RLC串联电路。若以 电源电压作为输入电压 ，以电容器两 端电压作为输出电压，此电路的传递 函数。并分析此为振荡电路的条件。 【解】 由基尔霍夫定律有
而流过电容的电流
其传递函数

自动控制原理实验典型环节的时域响应

自动控制原理实验典型环节的时域响应

实验名称：典型环节的时域响应一、目的要求1、熟悉并掌握TD-ACC+(或TD-ACS)设备的使用方法及各典型环节模拟电路的构成方法。

2、熟悉各种典型环节的理想阶跃响应曲线和实际阶跃响应曲线。

对比差异分析原因。

3了解参数变化对典型环节动态特性的影响。

二、原理简述1、比例环节传递函数：Uo(s)/Ui(s)=K.2、积分环节传递函数：Uo(s)/Ui(s)=1/TS3、比例微分环节传递函数：Uo(s)/Ui(s)=K+1/TS4、惯性环节传递函数： Uo(s)/Ui(s)=K/(TS+1)5、比例微分环节传递函数：Uo(s)/Ui(s)=K[(1+TS)/(1+τS)]6、比例积分微分环节传递函数：Uo(s)/Ui(s)=Kp+1/TiS+TdS三、仪器设备PC机一台，TD-ACC（或TD-ACS）实验系统一套四、线路视图1、比例环节2、积分环节3、比例积分环节4、惯性环节5、比例微分环节6、比例积分微分环节五、内容步骤1、按所列举的比例环节的模拟电路图将线连接好，检查无误后开启设备电源。

2、将信号源单元的“ST”端插针与“S”端插针用短路块短接，。

将开关设在方波档，分别调节调幅和调频电位器，使得“out”端输出的方波幅值为1V，周期为10S左右。

3、将2中的方波信号加至环节的输入端Ui，用示波器的“CH1”和“CH2”表笔分别检测模拟电路的输入Ui端和输出端Uo端，观测输出端的实际响应曲线Uo（t），记录实验波形及结果。

4、改变几组参数，重新观测结果。

5、用同样的方法分别搭接积分环节、比例积分环节、比例微分环节、惯性环节、比例积分微分环节的模拟电路图。

观测这些环节对阶跃信号的实际响应曲线，分别记录实验波形及结果。

六、数据处理1、比例环节①R0=200K,R1=100K;②R0=200K,R1=200K;2、积分环节①R0=200K,C=1uF;②R0=200K,C=2uF;3、比例积分环节①R0=R1=200K,C=1uF;②R0=R1=200K,C=2uF;4、惯性环节①R0=R1=200K,C=1uF;②R0=R1=200K,C=2uF;5、比例微分环节①R0=R2=100K,R3=10K,C=1uF,R1=100K;②R0=R2=100K,R3=10K,C=1uF,R1=200K;6、比例积分微分环节①R2=R3=10K,R0=100K,C1=C2=1uF,R1=100K;②R2=R3=10K,R0=100K,C1=C2=1uF,R1=200K;七、分析讨论在误差允许的情况下，输出的结果与理论值相符。

典型环节分析实验报告

典型环节分析实验报告

一、实验目的1. 理解并掌握典型环节（比例、惯性、比例微分、比例积分、积分、比例积分微分）的原理及其在控制系统中的应用。

2. 通过实验验证典型环节的阶跃响应特性，分析参数变化对系统性能的影响。

3. 熟悉MATLAB仿真软件的使用，掌握控制系统仿真方法。

二、实验原理控制系统中的典型环节是构成复杂控制系统的基础。

本实验主要研究以下典型环节：1. 比例环节（P）：输出信号与输入信号成比例关系，传递函数为 \( G(s) = K \)。

2. 惯性环节：输出信号滞后于输入信号，传递函数为 \( G(s) = \frac{K}{T s + 1} \)。

3. 比例微分环节（PD）：输出信号是输入信号及其导数的线性组合，传递函数为\( G(s) = K + \frac{K_d}{s} \)。

4. 比例积分环节（PI）：输出信号是输入信号及其积分的线性组合，传递函数为\( G(s) = K + \frac{K_i}{s} \)。

5. 积分环节（I）：输出信号是输入信号的积分，传递函数为 \( G(s) =\frac{K_i}{s} \)。

6. 比例积分微分环节（PID）：输出信号是输入信号、其导数及其积分的线性组合，传递函数为 \( G(s) = K + \frac{K_i}{s} + \frac{K_d}{s^2} \)。

三、实验设备1. 计算机：用于运行MATLAB仿真软件。

2. MATLAB仿真软件：用于控制系统仿真。

四、实验步骤1. 建立模型：根据典型环节的传递函数，在MATLAB中建立相应的传递函数模型。

2. 设置参数：设定各环节的参数值，例如比例系数、惯性时间常数、微分时间常数等。

3. 仿真分析：在MATLAB中运行仿真，观察并记录各环节的阶跃响应曲线。

4. 参数分析：改变各环节的参数值，分析参数变化对系统性能的影响。

五、实验结果与分析1. 比例环节：阶跃响应曲线为一条直线，斜率为比例系数K。

2. 惯性环节：阶跃响应曲线呈指数衰减，衰减速度由惯性时间常数T决定。

2-4 典型环节及其传递函数

2-4 典型环节及其传递函数

∫
G ( s ) = R / Ts ，这也是一个积分环节。从物理意义上说，由于液箱的液容 Ｃ 太大，或液阻 Ｒ
太大，液箱流出水量不足以影响液位，如果流入水量不变，液位将随时间不断增高（积分作 用）。 另外对直流伺服电动机，由于电气时间常数和机电时间常数大小，忽略不计时，该电动 机以转速为输出量，电枢电压为输入量时的动态特性成为比例环节，其传递函数为 N (s) G( s ) = =k U a (s) 如以电动机输出轴转角为输出量，相应的传递函数是 a ( s) k G( s ) = = U a (s) s 这是一个积分环节。可见，对于同一部件，不同输入或不同输出时，其传递函数是不同的。 最后，考虑气动仪表中常用的气容，它是一个气体容室能储存或放出气体，对气体量的 变化起惯性作用，类似于电路中的电容，见图 ２－２０。 通常采用“气容”这个概念来定量地表示气室储存气体的能力，其定义为 ∆m C= ∆p 式中， 是空气储存量的增量； ∆m ∆p 是气室压力的增量。 气体的质量流量（ｋｇ／ｓ）为 ∆q (t ) = d (∆m ) / dt
5
R2 R1
Ui Ri
图 2-23 运算放大器 组成的一阶惯性环节
−
+
C
U0
式中，时间常数 Ｔ＝ＲＣ。 实际上这是纯微分环节与一阶惯性环节相串联后构成的环节；当时间常数 Ｔ＜＜１ 时，一阶 惯性环节相当于 １：１ 的比例环节，因而总的传递函数相当于微分环节的传递函数。 当然也可以用运算放大器来组成微分环节，如 R 图 ２－２４ 所示。 该运放电路的传递函数为 if C U 0 (s) Ui G( s ) = = − RCs U i (s) U0 这就相当于一个纯微分环节。 + i
−
2

典型环节的传递函数

典型环节的传递函数
典型环节的传递函数
1、比例环节 凡输出量与输入量成正比，输出不失真也不延迟 而按比例地反映输入的环节，称为比例环节又叫 放大环节、无惯性环节、零阶环节
•动力学方程为：
xotKxit
•传递函数为：
Gs
Xo s Xi s
K
典型环节的传递函数
2、积分环节(纯积分环节) 凡输出量与输入量的积分成正比，称为积分环节， 又称为理想积分环节
•动力学方程为：
Tdxdottxotxit
•传递函数为：
GsXXoi ss
1 Ts1
典型环节的传递函数
5、导前环节(一阶微分环节) 又称为一阶微分环节，是一个相位超前环节。
•传递函数为：
GsXXoi ssTs1
典型环节的传递函数
6、振荡环节(二பைடு நூலகம்积分环节) 振荡环节是二阶环节，又称二阶振荡环节
•传递函数为：
•动力学方程为：
xotT1xi tdt
•传递函数为：
Gs
Xo s Xi s
1 Ts
典型环节的传递函数
3、微分环节(纯微分环节) 凡输出量与输入量的微分成正比，称为微分环节， 又称为理想微分环节
•动力学方程为：
xo
t
T
dxi t
dt
•传递函数为：
Gs
Xo s Xi s
Ts
典型环节的传递函数
4、惯性环节(一阶积分环节) 又称一阶惯性环节，是一个相位滞后环节。
G sX Xo isss22 n 2 nsn 2
GsX Xo issT2s22 1Ts1
典型环节的传递函数
7、二阶微分环节
•传递函数为：
G sX Xo isss22 n 2 nsn 2 GsX Xo issT2s22Ts1

2.3 传递函数 2.4 典型环节的传递函数

2.3 传递函数 2.4 典型环节的传递函数

2.4.3 微分环节
经过拉氏变换后得到
k sX o ( s) 2 X o ( s) sX i ( s) AR
得到传递函数
X o ( s) s Ts G( s) X i ( s) s k Ts 1 A2 R
A2 R T k
由上面传递函数形式看出，液压阻尼器是包含有惯性环 节和微分环节的系统，称之为具有惯性的微分环节。 若|Ts|<<1时，G(s)≈Ts，系统近似成为理想微分环节。
上海大学 机电工程与自动化学院
2.4.2 惯性环节
例题1 求图示质量-弹簧-阻尼器环节传递函数。 xo(t) xi(t) 解： 若质量m相对很小，可 k
略去其影响(忽略惯性力)。此 时的系统动力学方程为 m c
质量-弹簧-阻尼器系统模型
dxo (t ) c kxo (t ) kxi (t ) dt
经拉氏变换后
csX o ( s) kXo ( s) kXi ( s)
系统传递函数为
惯性环节的 时间常数
X o ( s) k 1 G(s) X i ( s) cs k Ts 1
上海大学 机电工程与自动化学院
c T k
2.4.2 惯性环节
例题2 求图示简单阻容电路的传递函数。 R 解：电路方程为
控制系统一般由若干元件以一定形式连接而成，从控制 理论来看，物理本质和工作原理不同的元件可以有完全相同 的数学模型。
在控制工程中，一般将具有某种确定信息传递关系的元 件、元件组或元件的一部分称为一个环节，经常遇到的环节 称为典型环节。 复杂控制系统常常由一些简单的典型环节组成，求出这 些典型环节的传递函数，就可以获得整个系统的传递函数。
压强
p2 p1 q Axi (t ) xo (t ) R

典型环节的传递函数

典型环节的传递函数

21
一、典型输入信号
1. 阶跃函数：
r(t)
a t 0
a
r(t) 0 t 0
t
单位阶跃函数：
1 t 0 r(t) 1(t) 0 t 0
单位阶跃函数的拉氏变换
R(s) L[1(t)] 1 s
22
2. 速度函数(斜坡函数)：
r(t)
at t 0
r(t)
0
t0
at
t
单位速度函数(斜坡函数)：
传递函数为： G(s)
1
s
积分环节原理图为：
U2(s) 1/ Cf s 1 1 U1(s) R1 R1C f s Tis
4
空载油缸
流量：
Q
f
(t)
A
dx(t) dt
X (s) 1/ A K Q f (s) s s
小惯性电动机
m(s) Km
Ua(s) s
三、理想微分环节 微分方程为：c(t) dr(t)
4. 调节时间ts:整个过渡过程所经历的时间，有时也叫过渡过 程时间。
30
5. 超调量σ%: 响应过程中，输出量
超出稳态值的最大偏差值， 一般用它与稳态值的比值 的百分数表示，即
% h(t p ) h() 100%
h()
6. 振荡次数N:单位阶跃响应曲线在0→ts时间内，穿越稳态 值次数的一半称为振荡次数。
31
7.稳态误差ess:对单位 负反馈系统，当时间t 趋于无穷时，系统单 位阶跃响应的期望值 [即输入量1(t)] 与实际值 (即稳态值)之差，定义为 稳态误差:
ess =1 - h(∞)
当h(∞) =1时，系统的稳态误差为零。
32
注意： σ%

自动控制原理--典型环节的频率特性

自动控制原理--典型环节的频率特性
j
j 1
0j 1
Im
0
Re
0
积分与微分环节
L(dB) 40
积分环节
0
微分环节
40
( )
90
微分环节
0 90
积分环节
20dB / dec
20dB / dec
6
三、微分环节
传递函数: G s s
频率特性:
G(j)
j
ej
π 2
➢1. 幅频特性 A及相频特性
A ,
A
( )
0
1
T
4
2
L,
0
1
T 3dB
4
20lg 2T 2 1
2
近似曲线 精确曲线
对数幅频特性和相频特性：
L() 20 lg 1 (T )2 () tg1 T
0 L0 0
1 L 20 lg 1 3
T
2
4
L
2
L()(dB) 0 0.1 5
10 15 20
0.2
0.3 0.4
0.6 0.8 1
T
2
34
6 8 10
七、一阶不稳定环节
传递函数: G s 1
Ts 1
➢1. 幅相频率特性
频率特性: G j 1
jT 1
G j
1
jT 1
1
1 T2
T
j1 T2
U
jV
U
1 2
2
V
2
1 2
2
一阶不稳定系统的幅相频
率特性是一个为（-1，j0）
为圆心，0.5为半径的半圆。
180O 90O
Im
1

2.4传递函数及典型环节传递函数

2.4传递函数及典型环节传递函数
典型环节示例 1 比例环节
输出量不失真、无惯性地跟随输入量， 两者成比例关系。
传递函数及典型环节的传递函数
比例环节的传递函数为：
传递函数及典型环节的传递函数
2 惯性环节： 凡运动方程为一阶微分方程
形式的环节称为惯性环节。其传递函数为：
K—环节增益（放大系数） T—时间常数，表征环节的惯性，和 环节结构参数有关
传递函数及典型环节的传递函数
如：有源积分网络
传递函数及典型环节的传递函数
液压缸
传递函数及典型环节的传递函数
5 二阶振荡环节 含有两个独立的储能元件，且所存储的 能量能够相互转换，从而导致输出带有 振荡的性质，运动方程为：
传递函数：
传递函数及典型环节的传递函数
振荡环节传递函数的另一常用标准形式为 （K=1）
无源微分网络
无源网络
显然，无源微分网络包括有惯性环节和微 分环节，称之为惯性微分环节，只有当 |Ts|<<1时，才近似为微分环节。
传递函数及典型环节的传递函数
除了上述微分环节外，还有一类一阶微分环 节，其传递函数为：
微分环节的输出是输入的导数，即输出反 映了输入信号的变化趋势，从而给系统以 有关输入变化趋势的预告。因此，微分环 节常用来改善控制系统的动态性能。
2) 传递函数是s 的复变函数。传递函数中的 各项系数和相应微分方程中的各项系数对应 相等，完全取决于系统结构参数；
传递函数及典型环节的传递函数
3) 传递函数是在零初始条件下定义的，即在零时 刻之前，系统对所给定的平衡工作点处于相对静 止状态。因此，传递函数原则上不能反映系统在 非零初始条件下的全部运动规律； 4) 传递函数只能表示系统输入与输出的关系,无 法描述系统内部中间变量的变化情况。

典型环节

典型环节

[G ( jω )]
1
ω →∞
0
G ( jω ) =
(1 − T ω ) + (2ζTω )
2 2 2
1
2
ωn ωn ωn
1 ω ≤ T
ς↑
ω →0
ς↓
2ζTω − arctan 1 − T 2ω 2 ∠ G ( jω ) = 2ζTω − π − arctan 1 − T 2ω 2
6、勾画出大致曲线。
①
②
当频率ω = 0 时，其开环幅相特性完全由比例环节和积分环 节决定。 节决定。 G 开环传递函数不含积分环节， 开环传递函数不含积分环节，即v = 0 时，( jω ) 曲线从正实 开始； 轴 开始；G ( j0) = K∠0° G 开环传递含有一个积分环节， 开环传递含有一个积分环节，即 v = 1 时， ( jω ) 曲线从负虚 π G 轴方向开始； 轴方向开始； ( j 0 ) = ∞ ∠ − 2 π G 曲线从负实轴方向开始； 当 v = 2 时，曲线从负实轴方向开始； ( j 0 ) = ∞∠ − 2 2 其余依次类推。 其余依次类推。 ，（即 中分母阶次n 当频率 ω = ∞ 时，若 n > m ，（即 G ( s ) 中分母阶次 大 于分子阶次m） 的模值等于0， 于分子阶次 ）其 G ( jω ) 的模值等于 ，相为 ( m − n ) π 。 2 即 π G ( j ∞ ) = 0∠ ( m − n ) 2
G ( jω) = G ( jω) e j∠G( jω) = u (ω) + jv (ω)
a) 令∠G ( jω ) = −π 。解出与负实轴交点处对应的频率 ω x 的值。再将 ω x 代入 G ( j ω ) 中，求得与负实轴交 的值。 点的模值。 点的模值。 b) 令 v (ω ) = 0 解出 ω x ，再将 ω x 代入 u (ωx ) 中求得与负 实轴交点的坐标。 实轴交点的坐标。

典型环节的传递函数

典型环节的传递函数

典型环节的传递函数
传递函数是一种表示线性时不变系统的方法，它可以表示为输入和输出之间的关系。

典型环节的传递函数是指在不同应用场景下，系统的输入和输出之间具有特定的数学关系。

下面列举一些常见的典型环节的传递函数：1、比例环节：
传递函数：G(s) = K
特性方程：y = Kx
2、一阶滞后环节：
传递函数：G(s) = K/(Ts+1)
特性方程：y(t) = Kx(t-t0)
3、积分环节：
传递函数：G(s) = Ks/(Ts+1)
特性方程：y(t) = K∫x(t) dt
4、微分环节：
传递函数：G(s) = Ks
特性方程：y(t) = Ky(t) + Kd/dt[y(t)]
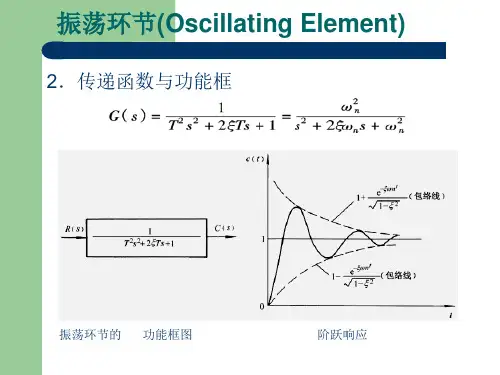
5、二阶振荡环节：
传递函数：G(s) = (K/T)(s^2+ω^2)/(s^2+2ζω_n s+ω_n^2)
特性方程：(T/K)(y''(t)+2ζω_n y'(t)+ω_n^2 y(t))=x''(t)+2ζω_n x'(t)+ω_n^2 x(t)
其中，K表示增益，T表示时间常数，s表示复变量，x表示输入，y 表示输出，ω_n表示无阻尼固有频率，ζ表示阻尼比。

自动控制原理_2.4典型环节传递函数

自动控制原理_2.4典型环节传递函数

B盘以角速度ω 转动时，因 B盘和I 轴
间以滑动键联接，故B盘滑动就会改变
偏心量e；当时e=0，A盘转动而 B盘不
转；e增大， B盘角速度ω 正比的增大， 设K为比例常数，B盘转角为θ (t)。 输入— e 输出—θ (t)
解： (t ) Ke(t )
(t ) K e(t )dt
di(t ) 1 ui (t ) L i(t ) R i(t )dt dt C 1 uo (t ) i(t )dt C
§2.4.6 延时环节（迟延环节）
xo (t ) xi (t )
τ为延迟时间
L[ x0 (t )] L[ xi (t )] G( s ) L[ xi (t )] L[ xi (t )]
当|Ts|<<1时，G(s)=Ts，
才近似为理想的微分环节。
此系统为包含有惯性环节及微分环节的系统。
（1）预见输入（ቤተ መጻሕፍቲ ባይዱ输入提前）
比例环节
R(s) r(t) t
1
1
X o ( s)
xo (t )
o
45
t

比例+微分
R(s) r(t ) t
1 Ts
X o ( s)
xo (t )
K G( s ) Ts 1
K为惯性环节的增益或放大系数；T为时间常数
理想的一阶惯性环节
1 G( s ) Ts 1
例1. 无源滤波电路
ui uo C为电容 R为电阻
1 ui (t ) i (t ) R i (t )dt C 解： 1 uo (t ) i (t )dt C 1 U i (t ) I ( s) R I (s) Cs LT得： 1 U o (t ) I ( s) Cs

典型环节传递函数-积分环节

典型环节传递函数-积分环节
4．举例
精品课件
输出量随着时间的增长而不断增加，增长的斜率为1/T。
1．微分方程
精品课件
积分环节(Integrating Element)
2．传递函数与功能框
积分环节的
功能框图
精品课件
阶跃响应
积分环节(Integrating Element)
3．动态Βιβλιοθήκη 反变换可得精品课件
积分环节(Integrating Element)
积分环节(Integrating Element)
积分环节的特点是它的输出量为输入量对时间的 积累。因此,凡是输出量对输入量有储存和积累特点的元 件一般都含有积分环节。如水箱的水位与水流量,烘箱的 温度与热流量(或功率),机械运动中的转速与转矩,位移与 速度，速度与加速度,电容的电量与电流等等。积分环节 也是自动控制系统中遇到的最多的环节之一。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.4 典型环节的数学模型P22
一、比例环节（Proportional Element）P23
二、惯性环节（Inertial Element） P23
三、积分环节（Integral Element）
P24
四、微分环节（Derivative Element） P26
五、振荡环节（Oscillating Element） P28
一、 比例环节
二、惯性环节（Inertial Element）P23
1.
动态微分方程：

dc(t) dt

c(t)

Kr(t)
2. 传递函数： 3. 阶跃响应
G(s) C(s) K
R(s) s 1
——时间常数 K——比通1 例系数
t
c(t) K (1 e )
过 原 点
惯性越大， 越大 当 t (3 ~ 4) 时，输出接近稳态值
5.零极点分布
j S平面
1 0
Re
只有一个极点

1

6.两个实例：
①
R2
u i R1 - C
+
②
R
ui
C
uo
Z1 R1,
而
Z2

R2 1 R2Cs
Uo(s) Z2
R2 R1
Ui (s) Z1 1 R2Cs
'
~ ui 为积分环节。
四、微分环节（Derivative Element） P26
理想微分环节：
1. 动态微分方程：
c(t)
dr(t)
dt
2. 传递函数
G(s) C(s) s
R(s)
——时间常数
3.单位阶跃响应
c(t) (t)
r(t)
1 0
C(t)
T
t
t
0
纯微分环节的阶跃相应曲线
2.4 典型环节的数学模型P22
思考题：
如何从该框图求得输出 与输入 之间的关系？
2.4 典型环节的数学模型P22
系统是由典型环节组成
常见的几种典型环节 比例、微分、积分、惯性、振荡、滞后
讨论内容
时域特征：微分方程，阶跃响应 复域（s域）特征：传递函数，零极点分布
有一个0值 极点
6.积分环节实
例① ：
C
R－
ui
＋
uo
② 电动机（忽略惯性和摩擦）
Ui (s) Uo(s)
R
1 Cs
Uo(s) 1 Ui (s) RCs
图中， 为转角， ' 为角速度。
ui
齿轮组

' kui


t
0 kui (t)dt
可见， ' ~ ui 为比例环节，
第二章 线性系统的数学模型
杜鹏英 dupy@
第二章 线性系统的数学模型
2.0 引言 2.1 线性系统的输入输出时域描述 2.2 拉普拉斯变换（Lapalase Transform） 2.3 线性系统的传递函数 Transfer Function P18 2.4 典型环节的数学模型 P22 2.5 系统的方框图（结构图）Block Diagram P28 2.6 信号流图及梅逊公式 2.7 非线性数学模型的线性化P20
uo
Uo(s) 1 Ui (s) RCs1
思考？
（1） RL电路
L
ui (t )
R
uo (t )
（2） 直流电机的励磁部分
L i f (t)
u f (t)
R
三、积分环节（Integral Element）P24
1.动态微分方程
t
c(t) K r(t)dt
0
K

1

2.传递函数
G(s) C(s) K 1
实例：
测速发电机输出电压与输入角度间的传递函数即 为微分环节。P28 图2-4-9
[实例]
①
R1
ui C
-
+
①
R1
u CR0
i
-
+
理想微分环节
uo
Uo(s) Ui (s)


R1Cs

Ts
比例微分环节
uoUo(s) R1(1 R0Cs) K(Ts1)
Ui (s)
R0
带有惯性的微分环节
四、微分环节（Derivative Element） P26
实际微分环节：微分环节和惯性环节串联
1.传递函数 2.阶跃响应
G(s) C(s) K s R(s) s 1
t
c(t) Ke
3.实例：P26 图2-4-5
四、微分环节（Derivative Element） P26
C
ui (t )
R
uo (t )
Uo (s) RCs Ui (s) 1 RCs
[实例]
R1
x(t)
C
R2 y(t)
Y (s) Z2(s) , X (s) Z1(s)
Z 2 R2,
Z1

R2

R1 1 R1Cs
G ( s ) Y ( s ) R 2 (1 R1Cs ) k (Ts 1) X ( s ) R1 R 2 R1 R 2Cs kTs 1
六、纯时间延时环节（又称存滞后环节） P29
一、 比例环节（Proportional
Element）
1. 动态微分方程： 2. 传递函数：
c(t)=Kr(t)
G(s) C(s) K R(s)
k为放大系数(增益)
3. 阶跃响应
4. 特点： 输入输出量成比例，无失真和时间延迟。
5. 实例： 电子放大器，齿轮，电阻（电位器），感应式变送器等。
比例微分环节：
1.传递函数
理想比例微分：
实际比例微分：
2.阶跃响应 r(t)
G(s) ( s 1) G(s) ( s 1)
s 1
c(t)
K
K
t
3.实例：P27 图2-4-7
t
四、微分环节（Derivative Element） P26
特点：
输出量正比输入量变化的速度; 能预示输入信号的变化趋势。
切
线
斜
率
为
阶跃响应
求单位阶跃输入的输出响应：
C(s) K
R(s) s 1
R(s) 1 , s
C(s) K K (1 1 )
s( s 1)
s s 1
c (t ) L1[C ( s )] K (1 e t )
二、惯性环节
4.特点：
对突变的输入其输出不能立即复现，有延迟； 非周期指数函数，无振荡；
R(s) s s
K—— 比例系数
— — 时间常数
3.单位阶跃响应
c(t)

1
t

Kt

c(t) c(t) Kr(t)
r(t) 1(t)
0t三ຫໍສະໝຸດ 积分环节（Integral Element）P24
4.特点：
输出量与输入量的积分成正比； 当输入消失，输出具有记忆功能
5.零极点分布
S平面
j
0 Re