当前位置：文档之家 › 第10章 能量法

第10章 能量法

  • 格式：ppt
  • 大小：1.76 MB
  • 文档页数：68

下载文档原格式

  / 68

合集下载

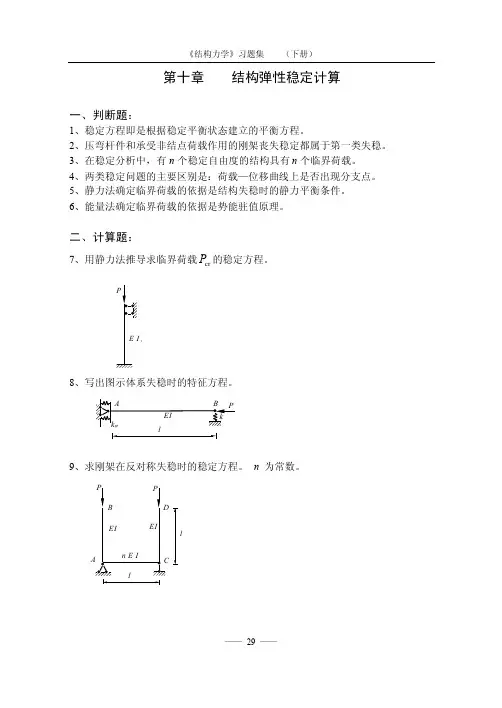
《结构力学》习题集及答案（下册）第十章结构弹性稳定计算

《结构力学》习题集及答案（下册）第十章结构弹性稳定计算

第十章 结构弹性稳定计算一、判断题：1、稳定方程即是根据稳定平衡状态建立的平衡方程。

2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。

3、在稳定分析中，有n 个稳定自由度的结构具有n 个临界荷载。

4、两类稳定问题的主要区别是：荷载—位移曲线上是否出现分支点。

5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。

6、能量法确定临界荷载的依据是势能驻值原理。

二、计算题：7、用静力法推导求临界荷载cr P 的稳定方程。

PE I ,l8、写出图示体系失稳时的特征方程。

k lEIk AB P9、求刚架在反对称失稳时的稳定方程。

n 为常数。

l Pl P n E IEIEI A C BD10、求图示完善体系的临界荷载cr P 。

转动刚度kl k r 2=，k 为弹簧刚度。

P l k r kl kEIO O EI O O11、求图示刚架的临界荷载cr P 。

已知弹簧刚度l EI k 33= 。

PEIlA BC lO O 0EI k12、求图示中心受压杆的临界荷载cr P 。

PEI l13、用静力法求图示结构的临界荷载cr P ，欲使B 铰不发生水平移动，求弹性支承的最小刚度k 值。

PlEI A Bk14、用静力法确定图示具有下端固定铰，上端滑动支承压杆的临界荷载crP。

P PEI yxδly15、用能量法求图示结构的临界荷载参数crP。

设失稳时两柱的变形曲线均为余弦曲线：yxh=-δπ(cos).12提示：cos d sin22u u u uabab⎰=+⎡⎣⎢⎤⎦⎥214。

PEIP2EI h3EA16、用能量法求中心受压杆的临界荷载crP与计算长度,BC段为刚性杆，AB段失稳时变形曲线设为：()y x a xxl=-().32EIPllEIABCyx→∞17、用能量法求图示体系的临界荷载cr P 。

l PEIEI 1=H18、用能量法求图示中心压杆的临界荷载cr P ，设变形曲线为正弦曲线。

第10章 杆件稳定性

第10章 杆件稳定性

(F )
a
II (大 挠 度 理 论) II (小 挠 度 理 论)
Fcr
B I (稳 定)
D'
O
a)
b)
第10章
两条平衡路径Ⅰ 的交点为分支点 分支点 B 将 分支点。 两条平衡路径 Ⅰ和 Ⅱ 的交点为 分支点 。
10.1 稳定性概念
原始的平衡路径Ⅰ分为两段：前段 OB 上的点属于稳定 原始的平衡路径Ⅰ 分为两段： 平衡， 上的点属于不稳定平衡。 平衡 ， 而后段 BC 上的点属于不稳定平衡 。 具有这种特 征的失稳形式称为分支点失稳形式。 征的失稳形式称为 分支点失稳形式。 分支点失稳形式
θ
例10.2
第10章
考虑如图(a)的单自由度非完善体 考虑如图(a)的单自由度非完善体 (a)
F k
B B'
系，刚性杆AB有初倾角 ε 。 刚性杆 有初倾角
k
10.1 稳定性概念
l
l
A
A
（a） ）
（b） ）
解：在图(b)中，平衡条件(水平方向)为 在图(b)中 平衡条件(水平方向) (b)
F tan(θ + ε ) − kl[sin(θ + ε ) − sin ε ] = 0 sin ε F = kl cos(θ + ε )[1 − ] sin(θ + ε )
第10章
例10.5
10.1 稳定性概念
如图所示， 如图所示，由三根相同的刚性杆组
成的系统，一端作用外力 ,铰结处B、 都是弹性 成的系统，一端作用外力F,铰结处 、C都是弹性 系数为k的弹性支座。试用两种方法求临界载荷。 系数为 的弹性支座。试用两种方法求临界载荷。 的弹性支座
第10章动载荷与交变载荷

第10章动载荷与交变载荷

3、交变应力：应力随时间作周期性变化，属疲劳问题。疲 劳破坏是指在反复载荷作用下，结构中裂纹形成、扩展乃至 断裂的过程。
4、振动问题： 求解方法很多。
4
工 程 力 学§10-2 构件作等加速直线运动
时的动应力计算
钢索起吊重物，W、a， 求：钢索 d
钢索具有a，不为平衡状态，不能用平
衡方程求内力。
kd
动荷因数
kd
FNd Fst
d st
d st
结论：只要将静载下的应力，变形，乘以动荷系数Kd即得 动载下的应力与变形。
6
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
冲击荷载问题的动响应
方法原理：能量法 ( 机械能守恒 ）
在冲击物与受冲构件的接触区域内，应力状态异常复杂， 且冲击持续时间非常短促，接触力随时间的变化难以准确分析， 放弃动静法。工程中通常采用能量法来解决冲击问题，即在若 干假设的基础上，根据能量守恒定律对受冲击构件的应力与变 形进行偏于安全的简化计算。
7
工 程 力 学§10-3 构件受冲击载荷作用件受冲击载荷作用时
的动应力计算
9
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
10
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
在冲击过程中，运动中的物体称为冲击物。 阻止冲击物运动的构件,称为被冲击物。
（3）、构件在交变应力作用下发生破坏需要经历一定数量的应 力循环，其循环次数与应力的大小有关。应力愈大，循环次数 愈少。
实验表明在静载荷下服从胡克定律的材料,只要应力不超 过比例极限 ,在动载荷下虎克定律仍成立且E静=E动.
动荷因数：
动响应 Kd 静响应
材料力学第十章杆件计算的能量法

材料力学第十章杆件计算的能量法


T
T
A

T
l
o
B


3.梁弯曲时的应变能
3.1 纯弯曲梁
l Ml
M
EI
W

1 2
M e
Vε
W

1 2
M
e

M 2l 2EI

M
l
3.2 剪切弯曲梁
弯矩M：
dVε M

M (x)2 dx 2EI
M (x)2 dx
Vε M l 2EI
剪力FQ：


6FQ
h2 (

y2)
0 2EI
l
2EI
FA

4
F2 A
l
3

F
l2 3

5FA Fl3
3EI 6EI 6EI
3.位移
Δ A

Vε FA

0
FA

5 16
F
例 求如图所示简支梁截面A的转角，设梁EI的为常数。
Mo A
M B
l
解：为了求A截面的转角A，可在A端加一虚力偶M0，如
图所示。则按卡氏第二定理，A截面的转角:
§10-2 杆件的弹性应变能
一、杆在基本变形下的应变能
1.杆在轴向拉伸（压缩）时的应变能
F
F
A
l l1
Vε

1 2
FN l

FN2l 2EA
dF F1 F
o
d(△l) △l1
B △l
2.圆杆扭转时的应变能
W 1 T
2
Mx T
M xl
GIP
弹塑性力学第十章

弹塑性力学第十章


( V
ijui),jdV V
i,jj
uidV
Snjijuid SVi,jjuidV
代入原虚位移方程
2019/10/27
34
§10-4 虚位移原理和最小势能原 理
代入原虚位移方程
V (i,jj fi)u id V S (X i n j i) ju id S 0
各向同性线性材料的应力应变关系
ijE 1(1)ijk kij
代入Uc表达式
Uc
1 2
VijijdV
1
U c2EV
(1)i2 j
kklldV
2019/10/27
10
§10-1 几个基本概念和术语
应变能、应变余能的计算举例
l
P
o
x
l
P
o
x
U

2P3l 3E2 A2

P 3l 3E 2A2
2019/10/27
14
§10-1 几个基本概念和术语
作业：图示结构各杆等截
面杆，截面面积为A,结点 A
C承受荷载P作用,材料应
力—应变关系分别为（1） l
y
=E ，(2) =E 1/2 。
试计算结构的应变能U 和 B
应变余能Uc。
2019/10/27
27
§10-3 功的互等定理
对于线弹性体本构关系
ij Eijkl kl
Eij kl kijli2j W k likjlEk lij
dVE dV (1) (2)
V ij ij
(1) (2) V ijkl kl ij
4
§10-1 几个基本概念和术语
能量法

能量法

第十章能量法承载的构件或结构发生变形时，加力点的位置都要发生变化，从而使载荷位能减少。

如果不考虑加载过程中其他形式的能量损耗，根据机械能守恒定律，减少了的载荷位能将全部转变为应变能储存于构件或结构内。

据此，通过计算构件或结构的应变能，可以确定构件或结构加力点处沿加力方向的位移。

但是，机械能守恒定律难以确定构件或结构上任意点沿任意方向的位移，也不能确定构件或结构上各点的位移函数。

应用更广泛的能量方法，不仅可以确定构件或结构上加力点处沿加力方向的位移，而且可以确定构件或结构上任意点沿任意方向的位移；不仅可以确定特定点的位移，而且可以确定梁的位移函数。

本章介绍的是：用应变能的概念，根据能量守恒原理来解决与弹性结构或构件变形有关问题的一般方法，这种方法称为能量法。

能量法既可用于计算构件或结构位移；也可用以解决静不定问题及其它一些问题；本章只讨论用能量方法计算位移。

§10.1 杆件的应变能计算前面我们曾讨论过拉伸（压缩）、扭转或弯曲时的变形计算。

但是在工程上还常遇到比较复杂的结构，例如图10-1中所示的桁架、刚架——是指由直杆组成的具有刚性结点的结构、拱——是指杆轴为曲线而且在铅垂载荷作用下会产生水平支座反力的结构等。

在计算这些结构上某一点或某一截面的位移时，能量法是比较简单的方法。

通过拉伸（压缩）、扭转、弯曲时的应变能分析，可见：杆件在受力变形后，都储藏有应变能。

若不计杆件变形过程中少量的热能等损失，则杆件能量守恒，外力在弹性体变形过程中所作的功W应等于杆件内储藏的应变能Vε，即Vε=W。

在第七章我们曾经分别得到等截面杆各横截面上的内力为常量时，拉伸（压缩）、扭转、弯曲（参看图10-2）时的应变能表达式如下拉伸（压缩）时2122NPF lV F lEAε=∆=此处F N=F P（10-1）圆轴扭转时 2122x P PM l V M GI εϕ== 此处M x =M P （10-2）平面弯曲时 2122P M lV M EIεθ== 此处M =M P （10-3）综合以上三个表达式中外力表达的部分，可以把应变能概括地写为12V W F εδ==(10-4) 式中 F ——在拉伸（压缩）时表示拉力（压力），在扭转或弯曲时表示集中力偶，所以此处F 称为广义力；δ——在广义力作用处与广义力F 相应的位移，称为广义位移，在拉伸（压缩）时它是与拉力（压力）相应的位移l ∆，在扭转时它是与扭转力偶矩相应的转角φ，在平面弯曲时它是与弯曲力偶矩相应的截面转角θ（如图2所示）。

材料力学第10章(动载荷)

材料力学第10章(动载荷)

突加荷载 h 0,
Kd 2
二、水平冲击 mg v
d
Fd d ， Pst st
Pst mg 其中： mgl st EA
Fd
st
Pst
mv2 冲击前：动 T1 能 2
冲击后： 应变能Vε 2 Fd d 2
2 F 2 st mv d mg
h
P
h
解：
st
Pl 1.7 102 (mm) EA
2h K d 1 1 st
2 500 1 1 243 2 1.7 10
l
l
d 2 A 4
P 2 103 0.028(MPa) st 4 A 7.1 10 d Kd st
假设： (1)冲击物为刚体； (2)不计冲击过程中的声、光、热等能量损耗（能量守恒）；
(3)冲击过程中被冲击物的变形为线弹性变形过程。(保守计算)
一、自由落体冲击
P
冲击前： T 0
V P(h d )
B
h
A
冲击后：
1 Vε d Fd d 2
A
Δd
能量守恒： T V Vd
B
2h st
l
4 Pl 3 22mm st 3 EI
K d 1 1 2 50 3.35 22
40 C 30
d Kd st
M max Pl 50(MPa) st W W
d Kd st 161 MPa) (
A
Δd
Fd
B
1 P (h d ) Fd d 2 Fd d P st
2 Fd 1 Fd P (h st ) st P 2 P
第10章 能量法

第10章 能量法

M n ( x) = − Px
EI L x
2
P A O
U =
∫
[M n ( x)]
L
2 EI
P 2 L2 dx = 6 EI
∂U PL3 = ③求位移 δ A = ∂P 3EI
例5(续): 求 A点的转角 解： ①求弯矩 M n ( x) = −(M 0 + Px) ②求变形能
U =
EI L x
P A O
N1 = N 2 cos α = Pctgα , N 2 =
对每个杆内能
2 2
P sin α
2
L
A N1 α
2
P
U =∫
L
[ N ( x)] dx + [ M T ( x)] dx + [ M n ( x)] dx = N
2 EA
∫
L
2GI p
∫
L
2 EI
L 2 EA
C
对整个杆系内能 N 12 l1 N 22 l 2 1 U = + = W = P yc 2 E A1 2 E A2 2 1 ( Pctg α ) 2 l1 l2 P 2 Py c = + ( ) 2 2 EA 1 2 EA 2 sin α
δ1 δi δn
δ2
Fi
Fn
1 n U = ∑ Fiδ i 2 i =1
二. 互等定理
1.功互等定理 Fi δ′ = Fjδ′ji ij
i 力在 j 力引起的位移δ’ij上 做的功等于j 力在 i 力引起 的位移δ’ji上做的功。
Fi
δ i′
i
0 Fj j
δ i′
i Fi
0
δ ij ′
δ j′
《材料力学》第十章 动载荷

《材料力学》第十章 动载荷

第十章 动 载 荷
基本要求: 基本要求: 了解构件作变速运动时和冲击时应力与变形的计 算。 重点: 重点: 1.构件有加速度时应力计算； 2.冲击时的应力计算。 难点： 难点： 动荷因数的计算。 学时： 学时： 4学时
第十章
§lO.1 概述
动 载 荷
§10.2 动静法的应用 §10.4 杆件受冲击时的应力和变形 §10.5 冲击韧性
( 2 )突然荷载 h = 0 : K
d
=2
△st--冲击物落点的静位移
五、不计重力的轴向冲击问题
冲击前∶
动能T1 = Pv 2 / 2 g 势能V1 = 0 变形能V1εd = 0
冲击后：
动能T2 = 0 势能V 2 = 0 变形能V 2εd = Pd ∆ d / 2
ห้องสมุดไป่ตู้
v P
冲击前后能量守恒，且
Pd = K d P
补例10-1 起重机钢丝绳的有效横截面面积为A , 已知[σ], 补例 物体单位体积重为γ , 以加速度a上升，试建立钢丝绳(不计自 重)的强度条件。 外力分析。 解：1.外力分析。包括惯性力 外力分析
惯性力：q a
x a L x m m a Nd qg +qa
=
γA
g
a
2.内力分析。 内力分析。 内力分析 3.求动应力。 求动应力。 求动应力
任何冲击系统都 可简化弹簧系统
能量法（机械能守恒） 三、能量法（机械能守恒）
冲击过程中机械能守恒。即动能 ，势能V，变形能V 冲击过程中机械能守恒。即动能T，势能 ，变形能 εd守恒 冲击前：系统动能为T， 势能为V=Q∆d， 变形能Vεd=0 冲击后：系统动能为0， 势能为V=0， 变形能Vεd
吉林大学材料力学考试大纲

吉林大学材料力学考试大纲

吉林大学材料力学考试大纲
要考的章数为1-14章。

第3章第9节不考弹簧应力和变形不考。

第4章第6节叠加法做弯矩图不考。

第5章第5节弯曲理论对某些问题的扩充不考。

第6章叠加法求弯曲变形不考。

第7章第10节莫尔强度理论和双剪理论不考。

第9章不考。

第10章第3节不考虚功原理不考。

第12章第5节不考。

第13章8节不考弯曲组合构件交变力计算知道公式推算不必计算。

第14章5、6、7节不考。

考试重点
一：画内力图（轴力•剪力•弯矩）
二：组合变形（拉•扭）静不定
三：压杆稳定，弯曲应力
四：应力状态•强度稳定
五：能量法•求位移，变形
六：冲击，动载荷
七：疲劳
八：求变形能（10章能量法）（非必考）（拉分题）（变形能基本公式推倒）
九：推倒公式（拉分题）
十：广义胡克定律
注：考试重点内容考的机率很大。

另外除了考试重点和不考范围之外的内容也要看，只是考的机率没那么大，但并非不考。

材料力学习题册2012.9.26

材料力学习题册2012.9.26

2－4螺旋压紧装置如下图。现已知工件所受的压紧力为F＝4 kN。装置中旋紧螺栓螺纹的内径d1＝13.8 mm；固定螺栓内径d2＝17.3 mm。两根螺栓材料相同，其许用应力 ＝53.0 MPa。试校核各螺栓的强度是否安全。
2－5现场施工所用起重机吊环由两根侧臂组成〔图a〕，A、B、C三处均为铰链连接。每一侧臂AB和BC都由两根矩形截面杆所组成〔图b〕。已知起重载荷FP＝1200 kN，每根矩形杆截面尺寸比例b/h，材料的许用应力 ＝。试设计矩形杆的截面尺寸b和h。
〔2〕轴的最大相对扭转角 。
3－5图示实心圆轴承受外加扭转力偶，其力偶矩Me=3 kN·m，图中尺寸单位为mm。试求：
〔1〕轴横截面上的最大切应力。
〔2〕轴横截面上半径r＝15mm以内部分承受的扭矩所占全部横截面上扭矩的百分比。〔3〕去掉r=15mm以内部分，横截面上的最大切应力增加的百分比。
3－6同轴线的芯轴AB与轴套CD，在D处二者无接触，而在C处焊成一体。轴的A端承受扭转力偶作用，如下图。已知轴直径d＝66 mm，轴套外直径D＝80 mm，厚度＝6 mm；材料的许用切应力[]＝60 MPa。试求结构所能承受的最大外力偶矩。
7－7已知矩形截面梁的某个截面上的剪力FQ=120kN，弯矩M＝10kN·m，截面尺寸如下图。试求1、2、3点的主应力与最大切应力。
7－8用实验方法测得空心圆轴外表上某一点〔距两端稍远处〕与轴之母线夹45°角方向上的正应变 。假设已知轴的转速n=120r/min(转／分)，材料的G=81GPa， ，试求轴所受之外力偶矩Me。(提示： 〕
5－13由号工字钢制成的ABD梁，左端A处为固定铰链支座，B点处用铰链与钢制圆截面杆BC连接，BC杆在C处用铰链悬挂。已知圆截面杆直径d＝20 mm，梁和杆的许用应力均为[]＝160 MPa，试求:结构的许用均布载荷集度[q]。

第十章 能量法

一、是非题10.1 杆系结构的变形能，等于各杆变形能之和。

（）10.2 弹性体变形能与加力次序无关，只与最后受力有关。

（）10.3 结构上的外力作功可能为正或负，因而结构的变形能有正负之分。

（）10.4 线性弹性结构的变形能可以叠加而非弹性结构的变形能不能叠加。

（）10.5 载荷与变形能之间必为非线形关系。

（）10.6以莫尔积分求各种结构在载荷作用下的位移时都可以采用图形互乘法。

（）10.7应用单位力法计算出结构在某处的位移值时在数值上就等于该单位力所做的虚功。

（）10.8若由载荷引起之弯矩图面积的代数和为零（=0 ），则不论其形心所对应的单位力弯矩图之值Mc 为何值，图乘所得必为零。

（）10.9超静定结构的多余约束数即等于建立力法方程的变形条件数。

（）10.10结构中的内力与应力只与结构受力和结构尺寸有关，与材料无关。

（）10.11变形协调法在本质上也是力法。

（）10.12力法的基本未知量均不能用静力平衡条件求得。

（）10.13温度变化和支座位移不会引起静定结构的内力，但一般会引起超静定结构的内力。

（）10.14力法基本方程均是根据结构支座处的位移约束条件建立的。

（）10.15n 次超静定结构的静定基可由解除结构任意n 个约束而得。

（）10.16力法正则方程适用于任何材料制成的小变形超静定结构。

（）10.17外力超静定结构必须解除外部多余约束而得到静定基。

（）10.18以力法求解超静定结构后经力平衡方程验算无误，说明结果正确。

（）二、选择题10.19设一梁在n 个广义力F 1 ，F 2 ，……，F n 共同作用下的外力功，则式中为（）。

A. 广义力F i 在其作用处产生的挠度B. 广义力F i 在其作用处产生的相应广义位移C. n 个广义力在F i 作用处产生的挠度D. n 个广义力在F i 作用处产生的广义位移10.20一根梁处于不同的载荷或约束状态，则（）A. 梁的弯矩图相同，其变形能也一定相同B. 梁的弯矩图不同，其变形能也一定不同C. 梁的变形能相同，其弯矩图也一定相同D. 梁的弯矩图相同，而约束状态不同，其变形能也不同10.21一梁在集中力F 作用下，其应变能为V e 。

材料力学第10章-能量法


10-4 卡氏定理
（2）先加载dFi ，则力 dFi 在其相应的位移 di上做的功为
1
W1 dFi di
2
F1
再加载F1, F2 ,, Fn ，在相应
的位移 i 上所做的功为
1
n1
W2 i1 2 Fi i V
F2
2
dFi Fi
di
i
n
Fn
原来载荷 dFi 对位移i 上所做的功为
W3 dFi i
F A
F
在位移坐标轴上取了一个微段d ，
该微段对应的外力可视为常力。则常力作
功为
dW Fd k d
B
当外载荷和相应的位移由零缓慢增加 O
d
至F 和 时，在这个过程中外力作功
k 2 F
W kd 0
2
2
SOAB
线弹性范围内，外载荷所做的功等于力与位移乘积的一半。
10-2 外载荷做的功
二、多个力作用下的外力功
量的损失），弹性体内部所贮存的应变能，在数
值上等于外力所作的功，即满足：
V W
l
P
利用功和能的概念来求解可变形固体的位移、变形和内力
等的方法，通称为能量方法。
10-2 外载荷做的功
一、单个力作用下的外力功
材料服从胡克定律，即在线弹性范围内，弹性体在外力
作用下位移 与外载荷F 成正比，即
F k
横力弯曲时，弯矩为x的函数，则横力弯曲时的应变能为
M (x)2 dx dV
2EI
M (x)2 dx
V l 2EI
四、用广义力和广义位移表示的应变能
轴向压力
扭转
弯曲
F l V 2
V M e

材料力学第十章


fC
1 EI
AC
M
(
x1
)
Fs
0
M ( x1 Fs
)
dx
)
f ( x) 1 EI
x 0
F
(l
x1
)(
x
x1
)dx1
Fx 2 6EI
(3l
x)
§10-4 卡氏第二定理
例10-5 图示悬臂梁AB，B端作用铅垂力F，梁的EI已知，
1)求梁的挠曲线方程；2)若在梁中截面再作用力F，求自
x2
F=F0
A
1)dx段应变能：
dU 1(A)( d
x
)
2
d
xA
FQ2dx
2
2G
2GA
dx dx
2)l段应变能：
U
l
0dU
0l
FQ2 dx 2GA
FQ—横截面剪力； A—横截面面积；
—截面系数
矩形：=6/5；实心圆：=10/9；薄圆环：=2；
3)注意：在一般细长梁中，远小于弯矩应变能的 剪力应变能，通常忽略不计。
若=0.3，h/l=0.1，比值为0.0312。长梁忽略剪切应变能。
3)求C点挠度：W
1 2
FfC
U弯
F 2l3 96EI
fC
Fl 3 48EI
§10-2 弹性应变能的计算
四、非线性固体的应变能
1．应变能
F 非线性
与比能：
U*
线性
非线性
u*
线性
2．余能与
F1
余比能：
U
d1
1 d
u
1
应变能：线弹性
F
由端挠度fB。

材料力学( 最新 )能量法


U W
• 10-2
杆件变形能的计算
P P
•轴向拉压 •轴力P与轴向变形成正比 •当轴力N沿轴向为变量时
N 2 ( x)dx dU udV dV Pl 2 2 EA N 2 ( x)dx dU 2 EA N 2 ( x)dx U dU l l 2 EA
' 4
1 1 U b P 3 P4 4 3 2 2
P3
P 4
A
B
1'
' 2
3
4
• 10-4
P 1
互等定理
P 2
A
P3
P 4
B
' 4 4
1
' 1
2
' 2
3
' 3
1 1 1 1 ' U1 P 1 P2 2 P 3 P4 4 P 1' P2 2 1 3 1 2 2 2 2 1 1 1 1 ' ' U 2 P 1 P2 2 P 3 P4 4 P 3 P4 4 1 3 3 2 2 2 2
U1 U 2
P 1' P2 2' P3 3' P4 4' 1
•功的互等定理
P P P P
' 1 1 ' 2 2 ' 3 3 ' 4 4
•第一组力在第二组力引起的位移上做的功，等 于第二组力在第一组力引起的位移上所做的功
' 当P2和P4等于零时 P 1' P3 3 1
V wA ε FP
FP2l 3 x 2dx 0 6 EI
l
FP l 3 wA () 3EI

第10章 能量法(作业解答)


=
1 EI
l 0
⎡ ⎢M ⎣
(x
)
∂M (x
∂M es
)
⎤ ⎥ ⎦
M
es
=
dx
0
=
qa 3 6EI
10-5 图示刚架，各杆的 EI 相等。试求截面 A 的位移和转角。
Bl F
x2
x1 A
1
1
1
h
C
解：用单位载荷法求解 如图所示，在截面 A 处分别作用一水平方向单位力、铅垂方向单
位力和一顺时针方向单位力偶，并分别求出由荷载 F 以及单位力和单 位力偶所引起的内力，列表计算如下：
∂Fs
当 a ≤ x ≤ l ， M (x) = −Fs (l − x)，
∂M (x) = −(l − x)
∂Fs
∫ yB
= ⎜⎜⎝⎛
∂U ∂Fs
⎟⎟⎠⎞Fs =0
=
1 EI
l 0
⎡ ⎢ ⎣
M
(x
)
∂M (x
∂Fs
)
⎤ ⎥ ⎦
Fs
=0
dx
∫ = q
a
(a
−
x)2 (l
−
x)dx
=
qa 3 (4l
−
a)
F=qa
q
面 A 和 B 之间的相对位移和相对转角。
A
F 对称轴 F
B
1
1
x1
h
x2
E
C
D
A
B
C
a
l
ql2/8
③
a
①②
解：用单位载荷法求解 由于结构和载荷的对称性，取刚架对称轴的一侧来求解 δ AB 和

材料力学填空与判断题解

F122-题132-题第 2 章 轴向拉伸与压缩二、填空题2-6 承受轴向拉压的杆件，只有在（加力端一定距离外）长度范围内变形才是均匀的。

2-7 根据强度条件][σσ≤可以进行（强度校核、设计截面、确定许可载荷）三方面的强度计算。

2-8 低碳钢材料由于冷作硬化，会使（比例极限）提高，而使（塑性）降低。

2-9 铸铁试件的压缩破坏和（切）应力有关。

2-10 构件由于截面的（形状、尺寸的突变）会发生应力集中现象。

三、选择题2-11 应用拉压正应力公式AN=σ的条件是（ B ） （A ）应力小于比极限；（B ）外力的合力沿杆轴线； （C ）应力小于弹性极限；（D ）应力小于屈服极限。

2-12 图示拉杆的外表面上有一斜线，当拉杆变形时，斜线将（ D ） （A ）平动；（B ）转动；（C ）不动；（D ）平动加转动。

2-13 图示四种材料的应力-应变曲线中，强度最大的是材料（A ），塑性最好的是材料（D ）。

2-14 图示三杆结构，欲使杆3的内力减小，应该（ B ）（A ）增大杆3的横截面积； （B ）减小杆3的横截面积； （C ）减小杆1的横截面积； （D ）减小杆2的横截面积。

2-15 图示有缺陷的脆性材料拉杆中，应力集中最严重的是杆（ D ）第 3 章 扭转二、填空题3-6 圆杆扭转时，根据（切应力互等定理），其纵向截面上也存在切应力。

3-7 铸铁圆杆发生扭转破坏的破断线如图所示，试画出圆杆所受外力偶的方向。

3-8 画出圆杆扭转时，两种截面的切应力分布图。

3-9 在计算圆柱形密围螺旋弹簧簧丝切应力时,考虑到(剪力引起的切应力及簧丝曲率的影响 ),而加以校正系数。

题24（A （B （C ）（D第3章 扭转3-10 开口薄壁杆扭转时，截面上最大切应力发生在(最厚的矩形长边 )处；闭口薄壁杆扭转时,截面上最大切应力发生在( 最小厚度)处. 三,选择题3-11阶梯圆轴的最大切应力发生在( D ) (A) 扭矩最大的截面; (B)直径最小的截面; (C) 单位长度扭转角最大的截面; (D)不能确定.3-12 空心圆轴的外径为 D ，内径为 d ，D d /=α。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2．扭转圆轴
1)应变能
U W
1 2
M
e
U T 2l 2GIp
若扭矩或截面直径为变量时
Me
l
a)分段变化
U
n
U
i1
i
in12TGi2Ilpi i
b)为杆长x的函数
U
0ldU
0l
T2 2GI
(
p
x) (x
dx )
2)比能
u
dU dV
0.5(A)(
dV
d
x)
A
2 G 2
2 2G 2
dx
dx
§10-2 弹性应变能的计算
1．广义力和广义位移 1)广义力泛指力与力矩； 广义位移为广义力所 F1 d1 直接产生的位移和转 角，如力产生位移， 力矩产生转角；
2)线弹性情况下，广义力与 广义位移成线性关系。
d2
F2
d3 F3
2．弹性应变能 1)弹性体中的应变能只决定于外力和位移的最终值， 与加力的次序无关；
§10-2 弹性应变能的计算
u
1
2
1
1
非线性
U W
d 0
1
Fdd
非线性
u
1
0
d
余能：线弹性 U*U 12F1d1 余比能：线弹性 u*u 12 11
非线性
U
*
F1 0
d
dF
非线性
u*
0
1
d
§10-3 互等定理
一、功和位移互等定理
1．推导：以简支梁为例
1)先加F1再加F2 ，二 力作的总功为
U1 W1 12F1d11 12F2d 22 F1d12
2)弹性应变能
a)等比例加载，使Fi同时由零到终值，则d i也同时由零
到终值；
b)引进参数b (0～1)，则有b Fi和与之对应的bd i，给b 一个增量db，则位移有相应的增量dbd i。
外力在位移增量上作的功为
dW (bFi dbFi )•(dbdi ) (Fid i )bdb c)外力总功 W dW (Fid i )01bdb (12Fid i ) d)弹性体中的应变能 U W (12Fid i )
U
U
弯
U
剪
F 2l3 96EI
F 2l
8GA
U
剪
2
l/2
0
2G A(
F 2
)2
dx
F 2l
8GA
U
剪
:U
弯
12EI
GAl 2
152(1
)(
h l
)
2
矩形截面梁： 6/5，I / Ah2 /12，G E/[2(1 )]
取 =0.3，h/l=0.1，上述比值为0.0312。可见对长梁可不考虑剪
切应变能。
3．弯曲
1)dx段应变能
d
dU
12 M
(
x
)d
1 2
M
(
x )dx
M(x)
M(x)
M 2 ( x)dx
2 EI
2)l 段应变能
dx
U
ldU
0
l 0
M2(x 2 EI
)dx
§10-2 弹性应变能的计算
4．剪切
1)dx段应变能
dU
12(A)(
d
x
)
2 d xA 2G
FQ2dx 2GA
A
2)l 段应变能
2)求C点挠度：由外力功等于应变能(W=U)，并忽略剪切应变能有
W
1 2
Ff
C
U弯
F 2l3 96EI
fC
Fl 3 48EI
§10-2 弹性应变能的计算
三、非线性固体的应变能
1．应变能
F 非线性
非线性
与比能
U*
线性
u*
线性
2．余能与 余比能
F1
1
U
u
d
d1
1
应变能：线弹性
U W
1 2
F1d
1
比能：线弹性
3K 2
F3 3 A3 K
2
4)由克罗第—恩格塞定理：d
BV
U * F
5F 2b A2K 2
C
R F
B x a
Fs
解：1)求铅垂位移fCV
CB段：M ( )
FRsin
，M (
F
)
Rsin
BA段：M ( x)FR，M ( x) R
F
fCV
1 EI
0/2F R3 sin2 d 0aFR2dx
FR2 ( R a) EI 4
2)求水平位移fCH：C点无水平力，虚加Fs
A
CB段：M BA段：M
)
Fx2
F
0
(
x2
l) 2
，
M ( x2 F
)
x2
f
B
1 EI
l/ 0
2
Fx12dx1
l l/2
Fx2
F
0
(
x2
l 2
)
x2dx2
7Fl 3 16EI
§10-4 卡氏第二定理
例10-6 图示桁架用幂强化材料制造，应力、应变关系为 =K 1/2(K为常
数)。两杆的横截面面积均为A，求集中力F作用点B处的位移。
F
A ① B dBH
解：1)使用节点分析法知： FN1 F ，FN2 2F
45o
dBV
=K 1/2
b
②
各杆中的应力为
1 F / A， 2 2F / A
2)①杆的余比能为
C 3)桁架总余能：U * (u1*
2u2*
)
Ab
5F 3 A2
3b K2
u1*
1 0
d
1 2
0 K2
d
3 1
第十章 能 量 法
• §10-1 概 述 • §10-2 弹性应变能的计算 • §10-3 互等定理 • §10-4 卡氏第二定理 • §10-5 虚功原理*
第十章 能 量 法
• §10-6 单位载荷法 • §10-7 图乘法(维利沙金法) • §10-8 瑞利—李兹法* • §10-9 超静定结构的基本解法 • §10-10 力法 正则方程* •小 结
1)求梁的挠曲线方程(用卡氏定理)；
2)若在梁中截面再作用集中力F，求自由端挠度fB。 x2
Fl+Fsx
x1 Fs
A
C
F Bx
x
F+Fs
l
解：1)求梁的挠曲线方程 在距梁左端x处虚加Fs
AC段：M (
x1 )
F (l
x1
) Fs
(
x
x1
)
，
M ( x1 Fs
)
x
x1
CB段：M ( x2
) F (l
x2
a)分段变化
b)为杆长x的函数
U
n
U
i1
i
in12FEN2iAlii
U
ldU
0
l FN2 ( x) dx 02EA( x)
2)比能
u dU dV
[FN2 ( x)dx]/[2EA( x)] A( x)dx
2
FN2 ( x EA2 (
) x
)
2 1
2E 2
1E
2
2
§10-2 弹性应变能的计算
§10-3 互等定理
二、互等定理的应用
例10-2 任意形状弹性体承受一对等值、反向、共线的力F作用，材料的
弹性常数为E、，试用功的互等定理，求弹性体的体积改变。
A F
d
A
B
F
p
p
p
B
p
解：1)设在同一个弹性体的表面上作用均匀压应力p
此时弹性体处于三向均压状态： 1 2 3 p
任意方向的线应变为： [ 1 ( 2 3 )]/ E (12 ) p/ E
克拉贝依隆原理：线弹性体应变能等于每一广义外力
与其产生广义位移乘积二分之一的总和。
§10-2 弹性应变能的计算
3)弹性应变能可以表达成外力或位移的唯一表达式，
称为外力的二次齐函数或位移的二次齐函数。
二、杆件应变能的计算
1．轴向拉伸或压缩
l
1)应变能
U
W
12FDl
U
FN2 l 2 EA
F Dl
若轴力FN或截面面积A为变量时
3)应变能是内力的函数，是外力的复合函数，计算偏微分
时，可先求内力对Fi的导数再积分
U
l
FN2 ( x 2 EA
)dx
l
M2(x 2 EI
)dx
lT2G2 (Ixp)dx
d
i
U Fi
l
FN ( EA
FN Fi
)dx
l
M EI
(
M Fi
)dx
lGTI
p
(
T Fi
)dx
§10-4 卡氏第二定理
a)只有轴力的桁架
(
(x
) )
FRsin Fs
FRFs ( R
Rx)(，1cMosF(sx)，)M( RF(s
) x)
R(1cos
)
fCH
(
U Fs
) Fs
0Leabharlann 1 EI0/2FR3
sin
(1cos
)d 0aFR( R
x )dx
FR( Ra)2 EI
§10-4 卡氏第二定理
例10-5 图示悬臂梁AB，B端作用铅垂集中力F，梁的EI已知，