第10章 能量法题解
- 格式:doc
- 大小:1.03 MB
- 文档页数:16



5.带电粒子在电场中的运动1.能用两种思路分析带电粒子在电场中的加速运动问题。
2.能用类平抛运动的分析方法研究带电粒子在匀强电场中的偏转问题。
3.能综合分析带电粒子在电场中的运动。
一、带电粒子在电场中的加速1.带电粒子的速度方向与电场强度的方向01相同或相反。
2.两种分析思路(1)利用02牛顿第二定律结合03匀变速直线运动公式来分析。
适合用于解决的问题:属于匀强电场且涉及运动时间等描述04运动过程的物理量。
(2)利用05静电力做功结合06动能定理来分析。
适合用于解决的问题:只涉及位移、速率等07动能定理公式中的物理量或08非匀强电场情景。
二、带电粒子在电场中的偏转1.带电粒子的初速度方向跟电场方向01垂直,静电力方向跟速度方向02不在同一直线上。
2.在匀强电场中,带电粒子的运动轨迹是一条03抛物线,类似04平抛运动的轨迹。
分析思路与分析05平抛运动一样。
(1)带电粒子在电场中不受重力。
( )(2)带电粒子仅在静电力作用下运动时,动能一定增加。
( )(3)带电粒子在匀强电场中偏转时,其速度和加速度均不变。
( )(4)带电粒子在匀强电场中无论是直线加速还是偏转,均做匀变速运动。
( )提示:(1)×(2)×(3)×(4)√课堂任务 带电粒子在电场中的加速仔细观察下列图片,认真参与“师生互动”。
活动1:图甲中粒子的受力情况如何?提示:受到向右的静电力和向下的重力,而重力远小于静电力,故重力可以忽略,这里认为粒子只受静电力。
活动2:图甲、乙中两极板间电场有什么区别?提示:图甲中两极板间的电场是匀强电场,图乙中两极板间的电场是非匀强电场。
活动3:图甲中若粒子无初速度释放,如何求粒子的末速度?提示:可以利用牛顿第二定律结合运动学公式求解:U =Ed ,F =Eq ,a =F m ,d =v 22a,得v=2Uqm ;还可以利用静电力做功结合动能定理求解:Uq =12mv 2-0,得v = 2Uqm。



第10章 结构的动力计算习题解答习题10.1 是非判断题(1) 引起单自由度体系自由振动的初速度值越大,则体系的自振频率越大。
( ) (2) 如果单自由度体系的阻尼增大,将会使体系的自振周期变短。
( ) (3) 在土木工程结构中,阻尼对自振周期的影响很小。
( )(4) 由于各个质点之间存在几何约束,质点体系的动力自由度数总是小于其质点个数。
( )(5) 多自由度的自振频率与引起自由振动的初始条件无关。
( ) (6) n 个自由度体系有n 个自振周期,其中第一周期是最长的。
( )(7) 如果考虑阻尼,多自由度体系在简谐荷载作用下的质点振幅就不能用列幅值方程的方法求解。
( )【解】(1) 错误。
体系的自振频率与初速度无关,由结构本身的特性所决定。
(2) 错误。
由阻尼结构的自振频率2r 1ωωξ=-可知,阻尼增大使自振频率减小,自振周期变长。
(3) 正确。
(4) 错误。
由动力自由度的概念知,动力自由度数与计算假定有关,而与集中质量数目和超静定次数无关。
(5) 正确。
(6) 正确。
(7) 正确。
习题10.2 填空题(1) 单自由度体系运动方程为2P 2()/y y y F t m ξωω++=,其中未考虑重力,这是因为__________。
(2) 单自由度体系自由振动的振幅取决于__________。
(3) 若要改变单自由度体系的自振周期, 应从改变体系的__________或__________着手。
(4) 若由式()211βθω=-求得的动力系数为负值,则表示__________。
(5) 习题10.2(5)图所示体系发生共振时,干扰力与__________平衡。
c k WF sin θ tP 12-2(5)习题 图习题10.2(5)图(6) 求习题10.2(6)图所示质点系的自振频率时(EI =常数),其质量矩阵[M ]=__________。
mm2m12-2(6)习题 图mF sin θ tP 12-2(7)习题 图习题10.2(6)图 习题10.2(7)图(7) 习题10.2(7)图所示体系不考虑阻尼,EI =常数。

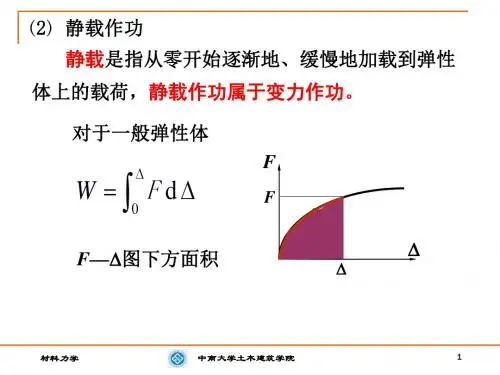

(名师选题)部编版高中物理必修三第十章静电场中的能量解题技巧总结单选题1、真空中相距为3a的两个点电荷M、N,分别固定于x轴上,x1=0和x2=3a的两点上,在它们连线上各点的电场强度E随x变化的关系如图所示,下列判断正确的是()A.点电荷M、N一定为同种电荷B.在x轴上,6a>x>3a的区域内,有一点电场强度为零C.点电荷M、N所带电荷量的绝对值之比为2:1D.若设无穷远处为电势零点,则x=2a处的电势一定为零答案:AA.若两电荷为异种电荷,则在x=2a处电场强度不可能为0,所以两电荷为同种电荷,故A正确;B.两电荷为同种电荷,在x轴上,只有一点电场强度为零,即2a处,故B错误;C.M在2a处产生的场强为E1=kQ1 (2a)2N在2a处产生的场强为E2=k Q2 a2由于2a处场强为零,故有E1=E2解得Q1=4Q2所以点电荷M、N所带电荷量的绝对值之比为4:1,故C错误;D.若设无穷远处为电势能零点,由于电荷从无穷远处到x=2a处电场力做功不为零,则x=2a处电势不为零,故D错误。
故选A。
2、平行板电容器保持与直流电源两极连接,充电平衡后,两极板间的电压是U,充电荷量为Q,两极板间场强为E,电容为C,现仅将两极板间距离减小,则引起的变化情况是()A.U变小B.C变小C.Q变大D.E不变答案:CA.电容器保持与直流电源两极连接,充完电后,电压U保持不变,A错误;B.根据C=εS 4πkd当极板间距离减小时,电容C增大,B错误;C.根据Q=CU 结合上述,电容增大,则Q变大,C正确;D.根据E=U d极板间距离减小,极板间电压不变,则场强E变大,D错误。
故选C。
3、水平光滑的绝缘木板上O点的正上方固定一正点电荷,其电荷量为Q,a、b、c为木板上以O为圆心的三个等间距同心圆。
现将一带正电的小球P从木板上O点附近静止释放,在小球依次经过a、b、c位置的过程中,下列说法错误的是()A.点电荷电场的电势逐渐降低B.点电荷电场的电场强度逐渐较小C.小球运动的加速度逐渐增大D.小球的电势能逐渐减小答案:CA.由正点电荷的电场线及等势面分布特点可知φa>φb>φc故A正确,不符合题意;和a、b、c三点到正点电荷的距离B.由点电荷的场强大小公式E=k Qr2r a<r b<r c可知E a>E b>E c故B正确,不符合题意;C.由F=qE可知小球P在三处所受电场力F1>F2>F3由牛顿第二定律可知小球P在三处的加速度大小a1>a2>a3故C错误,符合题意;D.由E p=qφ可知正电荷在电势高的地方电势能大,小球P在三处的电势能E pa>E pb>E pc故D正确,不符合题意。

在线测试题试题库及解答第十章结构动力学基础一、单项选择题1、结构的主振型与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案 A2、结构的自振频率与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案 A3、单自由度体系在简谐荷载作用下,下列哪种情况内力与位移的动力系数相同?A、均布荷载作用B、荷载作用在质点上与质点运动方向垂直C、荷载不作用在质点上D、惯性力与运动方向共线标准答案 D4、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案 D5、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案 D6、当简谐荷载作用于有阻尼的单自由度体系质点上时,若荷载频率远远大于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、重力C、阻尼力D、惯性力标准答案 D7、设ω为结构的自振频率,θ为荷载频率,β为动力系数下列论述正确的是A、ω越大β也越大B、θ/ω越大β也越大C、θ越大β也越大D、θ/ω越接近1,β绝对值越大标准答案 D8、如果体系的阻尼增大,下列论述错误的是A、自由振动的振幅衰减速度加快B、自振周期减小C、动力系数减小D、位移和简谐荷载的相位差变大标准答案 B9、无阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力C、惯性力与弹性力的合力D、没有力标准答案 D10、有阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力与弹性力的合力C、惯性力D、阻尼力标准答案 D11、当简谐荷载作用于无阻尼的单自由度体系质点上时,若荷载频率远远小于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、阻尼力C、惯性力D、重力标准答案 A12、一单自由度振动体系,其阻尼比为ξ,动力系数β,共振时下列结果正确的是A、ξ=0.05,β=10B、ξ=0.1,β=15C、ξ=0.15,β=20D、ξ=0.2,β=25标准答案 A13、一单自由度振动体系,由初始位移0.685cm,初始速度为零产生自由振动,振动一个周期后最大位移为0.50cm,体系的阻尼比为A、ξ=0.05B、ξ=0.10C、ξ=0.15D、ξ=0.20标准答案 A14、在低阻尼体系中不能忽略阻尼对什么的影响?A、频率B、主振型C、周期D、振幅标准答案 D15、单自由度体系受简谐荷载作用,ω为体系自振频率,θ为荷载频率,动位移 y(t)与荷载 P(t) 的关系是A、当θ/ω>1时,y(t)与P(t)同向,当θ/ω<1时,y(t)与P(t)反向。
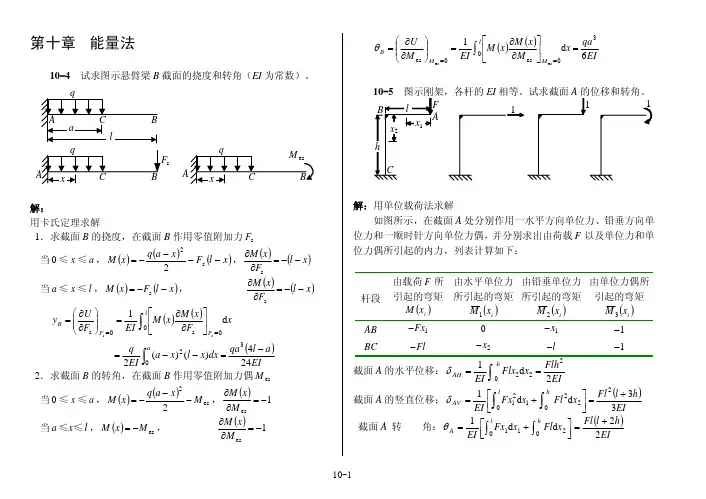
高中物理第十章静电场中的能量知识点总结归纳单选题1、在x轴上O、P两点分别放置电荷量为q1、q2的点电荷,一个带负电的试探电荷在两电荷连线上的电势能E p随x变化关系如图所示,其中A、B两点电势能为零,BD段中C点电势能最大,则()A.q1和q2都是正电荷且q1>q2B.B、C间场强方向沿x轴负方向C.C点的电场强度大于A点的电场强度D.将一个正点电荷从B点移到D点,电场力先做正功后做负功答案:DA.由题图可知,从O到P电势能一直减小,试探电荷带负电,则电势一直增加,两个点电荷必定是异种电荷,故A错误;B.由题图可知,从B到C电势能增加,试探电荷带负电,则电势降低,根据沿电场线方向电势降低可知,B、C间电场强度方向沿x轴正方向,故B错误;C.根据E p−x图像的切线斜率表示电场力,可知C点场强为零,A点的场强不等于零,则A点的场强大于C点的场强,故C错误;D.由题图可知,从B点到D点,试探电荷带负电,电势能先增大后减小,则电势先降低后升高,将一个正点电荷从B点移到D点,电势能先减小后增大,则电场力先做正功后做负功,故D正确。
故选D。
2、C1和C2两空气电容器串联以后接电源充电。
在电源保持联接的情况下,在C2中插入一电介质板,则()A.C1极板上电荷增加,C2极板上电荷增加B.C1极板上电荷减少,C2极板上电荷增加C.C1极板上电荷增加,C2极板上电荷减少D.C1极板上电荷减少,C2极板上电荷减少答案:AC1和C2两空气电容器串联以后接电源充电,稳定后两电容器所带电荷量相同;在C2中插入一电介质板,由C=εrS 4πkd可知,C2电容量增大,在电源保持联接的情况下,电势差不变,由C=Q U可知,C2极板上电荷增加,稳定后两电容器所带电荷量相同,C1极板上电荷增加。
故选A。
3、一正点电荷形成的电场,如图实线是其中的三条电场线,另一带电的点电荷从M点射入电场,仅受电场力作用下沿图中虚线运动到N点,则该点电荷从M向N运动的过程中()A.动能一直增加B.合力一直减小C.电势能一直减少D.动能和电势能的总和一直减少答案:BAC.由电场的性质和曲线运动的特点可知,电场力的方向始终与速度方向成钝角,对电荷做负功,电荷的动能减少、电势能增加,选项A、C错误;D.只有电场力做功时,电荷电势能与动能的总和保持不变,选项D错误;B.电场线的疏密表示电场强度的大小,M点处比N点处的电场线密,所受电场力FM>FN所以合力一直减小,选项B正确。
通用版带答案高中物理必修三第十章静电场中的能量微公式版解题技巧总结单选题1、两个可看成点电荷的物体,所带的电荷量分别为2q和−q,两者在空间的电场线分布如图所示,以−q为圆心做圆,a、b两点为圆和两电荷连线的交点,过−q的中心做两电荷连线的垂线,c、d两点为垂线和圆的交点,以无穷远为电势零点,点电荷在空间某点与电荷距离为r处产生的电势为φ=kq,以下说法正确的是()rA.a点的场强小于b点的场强B.a点的场强小于d点的场强C.电子沿圆弧从a点经c点到b点,电势能一直增大D.电子沿圆弧从a点经c点到b点,电势能先减小后增大答案:CA.两点荷在a点产生的场强方向相同,在b点产生的方向相反,−q在圆上产生的场强大小相同,2q在a点产生的场强大于在b点产生的场强,根据矢量叠加,a的场强大于b点的场强,A错误;B.同时2q在a点产生的场强大于在d点产生的场强,且两电荷在d点产生的夹角大于零,a的场强大于d点的场强,B错误;CD.电势是标量,根据公式φ=kq r−q在圆上产生的电势相等,且为负值,从a经c到b,2q产生的电势越来越小,且为正值。
则φa>φc>φb电子沿圆弧从a经c到b,电势能一直增大,C正确,D错误。
故选C。
2、静电除尘装置如图所示,它由金属管A和管中金属丝B组成,A接高压电源的负极,B接高压电源的正极,关于静电除尘的原理,下列说法正确的是()A.煤粉等烟尘在靠近B时被电离成正、负离子B.因为金属外壳接地,所以B的电势比A的电势高C.煤粉等烟尘吸附电子后被吸在B上D.煤粉等烟尘吸附电子后被吸在A上,最后由于重力的作用掉落在装置底部答案:BA.由题意可知靠近B的空气被电离,煤粉等烟尘吸附正离子后带正电,A错误;B.A接高压电源的负极,B接高压电源的正极,所以B的电势比A的电势高,B正确;C.因为A接高压电源的负极,煤粉等烟尘吸附正离子后被吸在A上,C错误;D.煤粉等烟尘吸附正离子后被吸在A上,最后由于重力的作用掉落在装置底部,D错误。
通用版带答案高中物理必修三第十章静电场中的能量微公式版解题方法技巧单选题1、小明同学用自制的验电器进行了一些探究实验。
如图所示,小明使验电器带了负电荷,经过一段时间后,他发现该验电器的金属箔片(用包装巧克力的锡箔纸制作)几乎闭合了。
关于此问题,他跟学习小组讨论后形成了下列观点,你认为正确的是()A.小球上原有的负电荷逐渐消失了B.在此现象中,正电荷从金属球转移到金属箔中,中和了负电荷C.小球上负电荷减少的主要原因是潮湿的空气将电子导走了D.该现象是由于电子的转移引起的,不再遵循电荷守恒定律答案:C带负电的验电器在潮湿的空气中,经过一段时间后,小球上的负电荷(电子)被潮湿的空气导走了,但电荷在转移的过程中仍然守恒,故C正确,ABD错误。
故选C。
2、如图所示,真空中固定两个等量异种点电荷A、B,其连线中点为O。
在A、B所形成的电场中,以O点为圆心、半径为R的圆面垂直AB,以O为几何中心、边长为2R的正方形abcd平面垂直圆面且与AB共面,两平面边线交点分别为e、f,g为圆面边缘上一点。
下列说法中错误的是()A.e、f、g三点电势均相同B.e、f、g三点电场强度均相同C.将一正试探电荷沿线段eOf从e移动到f过程中试探电荷受到的电场力一定先增大后减小D.若给某一正电荷一个合适的初速度,此电荷可以绕图示圆周做圆周运动答案:DA.整个圆面为等势面,因此e、f、g三点电势均相同,A正确;B.等势面与电场线垂直,可知e、f、g三点场强的方向相同;由于三点到A、B的距离完全相同,根据对称性,可知场强的大小也相同,B正确;C.在AB连线中垂线上,O点的场强最大,从O点向外逐渐减小,因此正试探电荷沿线段eOf从e移动到f过程中试探电荷受到的电场力先增大后减小,C正确;D.若正电荷在该圆周上,所受电场力与该平面垂直,不会指向圆心,不可能提供向心力,因此只在电场力的作用下,不可能绕图示圆周做圆周运动,D错误。
故错误的选D。
第10章 习题解答10-1 两根材料相同的圆截面直杆,其形状和尺寸如图所示。
试比较两杆的变形能。
解:22222d E lF EA l F U a a π== 2222222287283241286d E l F d E l F d E l F EA lF EA l F U a b b π=π+π=⋅+⋅=716872==b a U U10-2 已知图示等截面外伸梁的抗弯刚度EI ,试求梁的变形能及A 截面的转角。
解:1. 支反力 l M F F C B 02==2. 弯矩AB 段:01M x M =)( (0≤x 1≤l /2)CB 段:2022x l M x M =)( (0≤x 2≤l /2) 3. 变形能 EI lM dx x l M dx M EI U ll 3421202022222020120=⎥⎥⎦⎤⎢⎢⎣⎡+=⎰⎰4. 位移 EI l M U M A 321200==θ ,EIl M A 320=θ()10-3 图示桁架各杆抗拉压刚度EA 均相等,试求桁架的变形能及C 点的水平位移。
(a )(b )(a )(b ) 3 (c )BF DB解:1. 支反力 F F Ax = ,2F F F B Ay == 2. 各杆长度 l l l 231== ,l l l l ===5423. 各杆轴力 由节点B 的平衡条件得F N 223=(压),25F N =(拉); 由节点 D 的平衡条件得02=N ,24FN =(拉);由节点C 的平衡条件得F N 221=(拉)。
4. 变形能 EA l F EA l F l F l F EA U 2222957.0412222222221=⎪⎪⎭⎫ ⎝⎛+=⎥⎥⎦⎤⎢⎢⎣⎡⨯⎪⎭⎫ ⎝⎛+⨯⎪⎪⎭⎫ ⎝⎛⨯= 5. 位移 EA l F F CH 2957.021=∆ ,EAFlCH 914.1=∆(→)10-4 图示等截面曲杆为1/4圆周,其抗弯刚度EI 已知,试求曲杆的变形能及B 点的铅垂位移。
解:1 弯矩 θ=θs i n FR M )( (0≤θ≤π/2)变形能 ⎰ππ=θ⋅θ=20322228sin 21EIR F Rd R F EIU 位移 EI R F F BV 82132π=∆EIFR BV43π=∆(↓) 10-5 图示阶梯形变截面圆轴两端承受扭矩M n 作用,d 2 = 1.5d 1,材料的切变模量G 已知,试求圆轴的变形能及圆轴两端的相对扭转角。
解:1. 圆轴扭矩 M n = T2. 变形能 ⎰=2011221l P ndx I M G U ⎰+2022221l P n dx I M G 124P GI l T =224P GI lT +41281776Gd l T π= 3. 位移 ϕT 2141281776Gd l T π= , 41811552Gd Tl πϕ=B的弹簧刚度k,试求截面C的挠度。
解:1. 支反力32FF A=,3FF B=2. 内力梁的弯矩:AC段1132FxxM=)((0≤x1≤l/3)BC段2231FxxM=)((0≤x2≤2l/3)弹簧轴力:3FN=3. 在C点施加单位力,单位力引起的内力梁的弯矩:AC段1132xxM=)((0≤x1≤l/3)BC段2231xxM=)((0≤x2≤2l/3)弹簧轴力:310=N4. 莫尔积分⎰=3121941lCdxFxEIv⎰+32222911ldxFxEI kFEIFlFk9243431313+=⎪⎭⎫⎝⎛⨯+(↓)10-7图示简支梁B端悬吊在直杆CB上,已知梁的抗弯刚度EI和杆的抗拉刚度EA,试求梁中点D的挠度。
解:1. 载荷引起的内力杆:2qlN=梁:AD段2212qxxqlxM-=)((0≤x≤l/2)2. 在D点施加单位力,单位力引起的内力杆:21=N梁:AD段xxM210=)((0≤x≤l/2)3. 莫尔积分EAqlaEIqlqlEAaxdxqxxqlEIvlD43845212212122422+=⋅⋅+⋅⎪⎭⎫⎝⎛-=⎰(↓)10-8 试求图示简支梁A 截面的转角,已知梁的抗弯刚度EI 。
解:1. 支反力 qa F A 41= ,qa F B 43=2. 弯矩 AC 段:1141qax x M =)( (0≤x 1≤a )BC 段: 22222143qx qax x M -=)( (0≤x 2≤a ) 3. 在A 截面施加单位力偶,单位力偶引起的支反力和内力支反力 a F A 210=(↓),aF B 210=(↑) 弯矩 AC 段: 11011x 2ax M -=)( (0≤x 1≤a ) BC 段: 2201x 2ax M =)( (0≤x 2≤a ) 4. 莫尔积分 ⎰⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=θa A dx x a qax EI0111211411⎰⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-+a dx x a qx qax EI 0222222121431EIqa 4873=)10-9 试求图示变截面梁A 截面转角和B 截面的挠度,已知材料的弹性模量E 。
解:1. 支反力 a M F A 20=(↓),aMF C 20=(↑)2. 弯矩 AC 段:1012x aM x M =)( (0≤x 1≤2a ) BC 段: 01M x M =)( (0≤x 2≤a ) 3. 计算A 截面转角在A 截面施加单位力偶,单位力偶引起的弯矩 AC 段: 11110-=x 2a x M )( (0≤x 1≤2a )BC 段: 020=)(x M (0≤x 2≤a )莫尔积分 ⎰-=⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛=θa A EI a M dx x a x a M EI20011106121221)(4. 计算B 截面挠度 在B 截面施加单位力,单位力引起的弯矩qAC 段: 1101x 2x M =)( (0≤x 1≤2a ) BC 段: 220x x M =)( (0≤x 2≤a )莫尔积分 120210421dx x a M EIv a B ⎰=EIa M dx x M EIa 651202020=+⎰(↓)10-10 已知图示组合梁的抗弯刚度EI ,试求中间铰B 左右两截面的相对转角。
(提示:在中间铰B 两侧加一对单位力偶,分别写出两边弯矩方程,并注意到中间铰处的弯矩为零。
) 解:1. 载荷引起的弯矩BA 段: 21qx 2x M =)( (0≤x ≤l ) 2. 在中间铰B 的两边施加一对单位力偶,单位力偶引起的弯矩BA 段: lxx M +=10)( (0≤x ≤l ) 3. 莫尔积分 EI ql dx l x qx EIl2471211302=⎪⎭⎫⎝⎛+=θ⎰10-11 外伸梁受力如图所示,M = Fl/4,已知抗弯刚度EI ,试用图乘法求D 点的铅垂位移和B 截面的转角。
解:分别画出集中力F 和力偶M 引起的弯矩图,在D 点施加铅垂单位力,在B 截面施加单位力偶,并分别画出单位力和单位力偶引起的弯矩图。
1. D 点的铅垂位移 ⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛⨯⨯-=84211l l Fl EI v DV ⎥⎦⎤⎢⎣⎡⨯⨯⎪⎭⎫ ⎝⎛⨯⨯+4324211l l Fl EI ⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛⨯+8441l l Fl EI EI Fl 38453=(↓)2. B 截面的转角M 14 Fl 4 Fl l (M F ) (M M ) (M 0)(M 0)D⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛⨯⨯=θ3128211l Fl EI B ⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛⨯-+41281l Fl EI EIFl l Fl EI 9661282112-=⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛⨯⨯-+10-12 图示外伸梁由于温差变化产生弯曲变形,已知梁顶面温度为t 1℃,梁底面温度为t 2℃(t 2>t 1),设温度沿梁高h 为线形变化,材料的线膨胀系数为α,试求自由端C 的挠度。
解:用单位载荷法求解。
1. 由于温差引起微段梁两端相对转角(参阅例10-7)hdxt t d )(12-=αθ2. 在C 端施加单位力,单位力引起弯矩AB 段: 110x lax M -=)((0≤x 1≤l ) CB 段: 220x x M -=)( (0≤x 2≤a )3. 自由端C 的挠度 101211dx h t t x la EIv l C ⎰-⎪⎭⎫ ⎝⎛-=)(α hl a a t t dx ht t x EIa211220122)()()()(+--=--+⎰αα计算结果为负, C 点的挠度向上。
10-13 图示刚架由于沿截面高度线性变化的温差而弯曲变形(不计杆的拉压变形),设外表面温度为t 1℃,内表面温度为t 2℃(t 2>t 1),AB 杆和BC 杆截面相同,高度均为h ,材料的线膨胀系数为α,试求自由端C 的水平位移、铅垂位移及转角。
解:用单位载荷法求解。
1. 由于温差引起微段杆两端相对转角(参阅例10-7)hdxt t d )(12-=αθ2. 在C 端施加向上铅垂单位力,单位力引起弯矩CB 段: 110x x M =)( (0≤x 1≤l )C CBA 段: l x M =)(20(0≤x 2≤l )10121dx ht t x l CV ⎰-=∆)(αht t l dx ht t ll 231222012)()(-=-+⎰αα 3. 在C 端施加向左水平单位力,单位力引起弯矩CB 段: 010=)(x M (0≤x 1≤l ); BA 段: 220x x M =)( (0≤x 2≤l )ht t l dx ht t x l CH 212220122)()(-=-=∆⎰αα 4. 在C 端施加单位力偶,单位力偶引起弯矩CB 段: 110=)(x M (0≤x 1≤l ) BA 段: 120=)(x M (0≤x 2≤l ))()()(ht t l dx h t t l C 12201222-=-=⎰ααθ10-14 图示桁架各杆抗拉压刚度均为EA ,试求节点B 的水平位移和BC 杆的转角。
解:1. 载荷引起各杆的轴力由节点B 的平衡条件得 N 1 = F (拉) ,N 2= F (压)由节点C 的平衡条件得 N 3 = F /2 (拉) 2. 在节点B 施加向右水平单位力,单位力引起的轴力由节点B 的平衡条件得 330201==N N (拉),由节点C 的平衡条件得6303=N (压)。
B 点的水平位移 EAFl EA Fl EA Fl EA Fl BH 1231233333-=--=∆ (←) (↑)(←)F3. 在BC 杆两端节点B 和C 各施加一垂直杆轴线的单位力,单位力引起的轴力 由节点B 的平衡条件得 33201=N (拉),3302=N (压),由节点C 的平衡条件得3303=N (压)。