当前位置：文档之家 › 第十三章 - 能量法.ppt-结构力学

第十三章 - 能量法.ppt-结构力学

  • 格式：ppt
  • 大小：1.71 MB
  • 文档页数：59

下载文档原格式

  / 59

合集下载

演示课件材料力学能量法.ppt

演示课件材料力学能量法.ppt

.精品课件.
14
先加F1后加F2 F1
F2
先加F2后加F1 F1
F2
不同加载次序外力功均相同，若按比例同时加载， 外力同时达到最终值，即比例加载，外力功不变。
.精品课件.
15
三、克拉贝依隆（Clapeyron)原理 线弹性体上，作用有载荷F1,F2 , … Fi, … Fn 与外力方向相应的位移为D1, D2, … Di, … Dn 由线弹性体的叠加原理，各位移是载荷的线性函数
……
Di*= di1F1 * +di2 F2 * + … +diiFi * … +dinFn *= lDi
……
注意：带星号上标的载荷和位移都是中间值，所 以是变数，随着l的变化而变化。
.精品课件.
18
Ve
W
n i 1
1 2
Fi Di
线弹性体的外力功或变形能等于每一外力与其 对应位移乘积之半的总和。
20
组合变形
M
据Clapeyron原理，
微段dx上
dVe
dW
1 2
FNd (Dl )
1 Mdq
2
1 Tdj
2
FN2dx M 2dx T 2dx
dx
2EA 2EI 2GIP
整个杆件的应变能为
Ve
FN2
(
x
)
dx
l 2EA
M2 (x)
dx l 2EI
T2 (x)
dx l 2GIP
T
FN
.精品课件.
9
已知：EI = 常数，用功能原理
F
计算A点的挠度。
A
B
解：①建立坐标系
wA

结构力学

结构力学
结构动力学
结构动力学是研究工程结构在动载荷作用下的响应和性能的分支学科。动载荷是指随时间而改变的载荷。在 动载荷作用下，结构内部的应力、应变及位移也必然是时间的函数。由于涉及时间因素，结构动力学的研究内容 一般比结构静力学复杂的多。（见结构动力学）
结构稳定理论
结构稳定理论是研究工程结构稳定性的分支。现代工程中大量使用细长型和薄型结构，如细杆、薄板和薄壳。
结构力学
基础学科
01 简介
03 发展简史 05 研究方法
目录
02 工作任务 04 学科体系 06 能量法
结构力学是固体力学的一个分支，它主要研究工程结构受力和传力的规律，以及如何进行结构优化的学科， 它是土木工程专业和机械类专业学生必修的学科。结构力学研究的内容包括结构的组成规则，结构在各种效应 （外力，温度效应，施工误差及支座变形等）作用下的响应，包括内力（轴力，剪力，弯矩，扭矩）的计算，位 移（线位移，角位移）计算，以及结构在动力荷载作用下的动力响应（自振周期，振型）的计算等。结构力学通 常有三种分析的方法：能量法，力法，位移法，由位移法衍生出的矩阵位移法后来发展出有限元法，成为利用计 算机进行结构计算的理论基础。
能量法
结构力学中的能量原理以内部和外部力量的能量或作业的形式表达应力，应变或变形，位移，材料特性和外 部影响之间的关系。由于能量是一个标量，这些关系为固体力学中可变形体的控制方程提供了方便和可选的方法。 它们也可以用于获得相当复杂系统的近似解，绕过了解一组控制偏微分方程的困难任务。
感谢观看
简介
结构力学是一门古老的学科，又是一门迅速发展的学科。新型工程材料和新型工程结构的大量出现，向结构 力学提供了新的研究内容并提出新的要求。计算机的发展，又为结构力学提供了有力的计算工具。另一方面，结 构力学对数学及其他学科的发展也起了推动作用。有限元法这一数学方法的出现和发展就和结构力学的研究有密 切关系。在固体力学领域中，材料力学给结构力学提供了必要的基本知识，弹性力学和塑性力学是结构力学的理 论基础。另外，结构力学与流体力学相结合形成边缘学科——结构流体弹性力学。

材料力学能量法

材料力学能量法

限制条件：不适 用于求解动力学 问题如振动、冲 击等
适用范围：适用 于求解线性问题 如弹性、塑性等
限制条件：不适 用于求解非线性 问题如塑性、蠕 变等
材料力学能量法的发展趋势和未来 展望
材料力学能量法的发展趋势
计算方法：发展高效、准确 的数值计算方法
应用领域：拓展应用领域如 航空航天、生物医学等
柱的压缩问题
问题描述：柱在轴向 压力作用下的压缩问 题
应用实例：桥梁、建 筑等结构中的柱在受 压时的变形和破坏
能量法分析：利用能 量法分析柱的受压变 形和破坏过程
结论：能量法在柱的 压缩问题中的应用可 以有效地预测柱的变 形和破坏情况为工程 设计提供依据。
弹性体的振动问题
添加 标题
弹性体振动问题的背景：在工程中弹性体的振动问题非常常见如桥梁、建筑物、机械设备等。
定义和原理
材料力学能量法： 一种研究材料力学 问题的方法通过分 析能量变化来求解 问题。
基本概念：能量、 应力、应变、位移 等。
原理：根据能量守 恒定律材料的变形 和破坏过程中能量 会发生变化通过分 析这些变化可以求 解问题。
应用：广泛应用于 结构分析、优化设 计等领域。
能量法的应用范围
结构力学：分析结构受力、变形和稳定性 材料力学：分析材料应力、应变和断裂 流体力学：分析流体流动、压力和速度 热力学：分析热传导、对流和辐射 电磁学：分析电磁场、电磁波和电磁感应 声学：分析声波传播、反射和吸收
能量法的基本假设
材料是连续、均匀、各向同性的
材料是线弹性的应力与应变成正 比
添加标题
添加标题
材料是弹性的满足胡克定律
添加标题
添加标题
材料是各向同性的应力与应变的 关系与方向无关

结构力学(全套课件131P) ppt课件

结构力学(全套课件131P) ppt课件

的两根链杆的杆轴可以平行、交叉，或延长线交于
一点。
当两个刚片是由有交汇点的虚铰相连时，两个刚
片绕该交点（瞬时中心，简称瞬心）作相对转动。
从微小运动角度考虑，虚铰的作用相当于在瞬时
中心的一个实铰的作用。
19
20
规则二 （三刚片规则）： 三个刚片用不全在一条直线上的三个单铰（可以
是虚铰）两两相连，组成无多余约束的几何不变体 系。
两个平行链杆构成沿平行方向上的无穷远虚铰。
三个刚片由三个单铰两两相连，若三个铰都有交 点，容易由三个铰的位置得出体系几何组成的结论 。当三个单铰中有或者全部为无穷远虚铰时，可由 分析得出以下依据和结论：
１、当有一个无穷远虚铰时，若另两个铰心的连 线与该无穷远虚铰方向不平行，体系几何不变；若 平行，体系瞬变。
３、通过依次从外部拆除二元体或从内部（基础、 基本三角形）加二元体的方法，简化体系后再作分 析。
41
第一部分 静定结构内力计算
静定结构的特性： １、几何组成特性 ２、静力特性 静定结构的内力计算依据静力平衡原理。
第三章 静定梁和静定刚架
§3-1 单 跨 静 定 梁
单跨静定梁的类型：简支梁、伸臂梁、悬臂梁 一、截面法求某一指定截面的内力
15
１、单约束（见图２-2-2） 连接两个物体（刚片或点）的约束叫单约束。
１）单链杆（链杆）（上图） 一根单链杆或一个可动铰（一根支座链杆）具
有１个约束。 ２）单铰（下图）
一个单铰或一个固定铰支座（两个支座链杆） 具有两个约束。 ３）单刚结点
一个单刚结点或一个固定支座具有３个约束。
16
２、复约束 连接３个（含３个）以上物体的约束叫复约束。
三、对体系作几何组成分析的一般途径

材料力学第十三章 能 量 法

材料力学第十三章 能 量 法

Vε Vε (D1 , D 2 ,, D i ,, D n )
假设位移 Di 有一微小增量 dDi 其它位移均保持不变 梁的应变能也有一增量 dVe
外力功的增量
d W Fi d D i
Ve d Ve d Di D i
d Ve d W
Ve Fi D i
卡氏第一定理
卡氏第一定理
Vε
l
0
F ( x) T ( x) dx dx 0 2GI 2 EA p
l
2 N
2
F ( x) M ( x) d x s dx 0 2 EI 0 2GA
l l
2
2 S
应变能恒为正 ，是内力或外力的二次函数。
非线性函数
一般情况：非线性弹性体
s s1 s e
外力作功：
de e 1
DAB 方向水平向外
§3-4 用能量法解超静定系统
解超静定问题要综合考虑三方面 几何方面 —— 建立变形几何相容条件 物理方面 —— 建立补充方程 静力学方面 —— 建立平衡方程
等直杆，发生基本变形，材料为线性弹性体 非等直杆或杆系结构，受较复杂荷载作用， 材料为非线性弹性体 易 难
能量法
例1：求图示超静定梁支座处的约束力。
③ 先加M，后加F
A
M AM
F
B
AF DCF
AM
Ml 3EI
D CF
Fl 48 EI
3
AF
Fl 16 EI
2
1 1 应变能： V M ε AM ( FD CF M AF ) 2 2 2 3 2 2 1 F l M l MFl ( ) EI 96 6 16
Ve Fi D i

材料力学第13章 能 量 法

材料力学第13章 能 量 法

基本变形下的外力功及杆件的变形能的计算 变形 类型 外力功 应变能(内力 为常力） 应变能(内力 为变力） 拉压 扭转 弯曲
1 Pl 2
1 T 2
1 M e 2
F l 2 EA FN ( x) l 2 EA dx
2
2 N
T 2l 2GI P T 2 ( x) l 2GI P dx
2
M l 2 EI
?
解：
Fi i W 2 i 1
n
PwA M A 2 2 P 2l 3 M 2l FMl 2 6 EI 2 EI 2 EI
3 Pl P wA 3EI
2 Ml M wA 2 EI
P A
Pl 2 EI
2
M A
Ml EI
例2: 弯曲刚度为EI的简支梁受均布荷载q作 q 用，如图所示。试求梁内的应变能 。
W dW F d
0 0
F F1
1
1
O
d
F
1
(a)
W dW F d
0 0
1
1
F F
F W 2
当载荷与相应的位移保持正 比关系，并且载荷由零逐渐 增加时，载荷所作之功为载 荷最大值与位移最大值乘积 的一半。 式中力F是广义力（力， 力矩）、Δ为广义位移（ 线位移，角位移）。
P a2 RB (3l a ) 2 2 l
§13－3
1.卡氏定理
卡氏定理
设图中材料为线性弹性体，求与广义力Fi对应 的广义位移Δi 。
1 2 3 n
B
1 2 3 n
根据克拉贝隆定理，由于应变能只与最后荷 载有关，而与加载顺序无关。外力功与应变 能为：
Fi i V W 2 i 1

能量法——精选推荐

能量法——精选推荐
2l
(Δ cosθ
)2
=
EAΔ2 2l
cos3 θ
△
对杆2,有:
V2
=
EA 2l
Δ2
∴有
V
= V1
+ V2
+ V3
=
EAΔ2 l
cos3 θ
+
EAΔ2 2l
外力的力函数为PΔ，故结构的总位能为:
∏
=V
−U
=
⎛ ⎜ ⎝
EAΔ2 l
cos3 θ
+
EAΔ2 2l
−
pΔ
⎞ ⎟
⎠
Pre
Next Exit
∵根据题意,Δ是未知的，现变化Δ满足δΠ= 0条件,故得:
δ
∏
=
∂Π ∂Δ
δΔ
=
⎛ ⎜⎝
2EAΔ l
cos3 θ
+
2EAΔ 2l
−
P
⎞ ⎟⎠
δΔ
=
0
从而得到: ( ) EAΔ 1+ 2 cos3 θ − P = 0 l
( ) 所以得:
Δ=
Pl
EA 1+ 2 cos3 θ
Δ求得后，即可求出各杆的力，可见用位能驻值原理的计算方法
是“位移法”，并且所得的就是力的平衡方程式。若以Π为纵坐标，
2 能量法
能量法是从能量的角度出发去描述结构的平
衡和连续,使力的平衡和变形连续同时满足,出发
点更高,是进一步研究结构的重要理论基础
§6-1 应变能与余能 (知识回顾)
普遍 弹性体的外载 的 与变形间的关 情况 ： 系为非线性的
①可能由于材料本身的 应力—应变间的非线性关系而引起

第十三章结构的稳定计算

第十三章结构的稳定计算

•由位移参数不全为零得稳定方程并求解：
Pl k

Pl
k Pl
k


0
展开得：只P2是 3理P论k 上存k 在2 的0 失稳(曲3)线
l l
解得：P1

0.38
k l
•求失稳曲线：将P1

P2 0.38
k2.代62入kl （, 1）Pc得r P11
l
结 •稳定性演算：高强度材料应用、结构形式的发展，结构
构
趋于轻型、薄壁化，更易失稳，稳定计算
日益重要。
2、平衡状态的三种情况
稳定平衡：在某个平衡状态，轻微干扰，偏离原位， 干扰消失，恢复原位。
中性平衡：由稳定平衡到不稳定平衡的中间状态。
不稳定平衡：在某个平衡状态，轻微干扰，偏离原位，
干扰消失，不能恢复原位。
Pcr
Pcr
原始平衡：轴向受压 新平衡形式：压弯组合
原始平衡：轴向受压
Pcr
新平衡形式：压弯组合
分支点失稳的特点：
原始平衡：平面弯曲 新平衡形式：斜弯曲加扭转
结构的变形产生了质的改变。即原来的平衡形式成为不稳定
而可能出现新的与原来平衡形式有质的区别的平衡形式，同时，
这种现象带有突然性。
5
5、极值点失稳：非完善体系出：现极极具承值值有受点点初偏失失曲心稳稳率荷的。的载特平压的点衡杆压：形杆非式完不善出体现系分
2）P>k/l ，当θ≠0，Π恒小于零（Π为负定） (即U<UP表示体系缺
少足够的应变能克服荷载势能，压杆不能恢复到原有位置) 。
当θ=0，Π为极大值0。原始的平衡状态是不稳定的。
3）P=k/l ，当θ为任意值时，Π恒等于零(即U=UP) 。 体系处

工科教材—材料力学完整成套课件第13章- 能量法

工科教材—材料力学完整成套课件第13章- 能量法
G
E
T0()cos, M 0()sin
2(1 )
B 0T (G )T Ip 0()R d 0M ()E M I0()R d 0mG coIsp 2Rd0msE inI2Rd
mR mR
GIp 2 EI 2
R
Rm 1
2 GIp
1
EI
32(2 )Rm
Ed4
例：轴线为半圆形的平面曲杆,位于水平面内, 在自由端受垂直力P作用。试求自由端A的垂直 位移、绕x轴的转角和绕y轴的转角。已知 GIp、 EI为常量
P0作功：
U0
P 1、 P2作 功 ： U
共做功
W1
U0
U
1
P 0在 上 又 作 功 ： 1
P1
P2
P0 1
C
W1 U1
U 0U1[(M (x)2 EM I0(x)]2dx l
M 2(x)d x[M 0(x)]2d xM (x)M 0(x)d x
l 2 E I l 2 E I
X 8a(l a)
(2)
ql2 / 8
CE 1IX 2 al2 3X2 a21q 1l232 1
0 X ql3
4a(2l 3a)
例：图示梁的抗弯刚度为EI，试求D点的 铅垂位移。
解：
vC
3 EI
Pa2 2
2a
3
Pa3 EI
例：图示开口刚架，EI=const。求A、B两 截面的相对角位移 θAB 和沿P力作用线方向的 相对线位移 ΔAB 。
N 2(x)
T2(x)
M 2(x)
Ul2EA (x)dxl2G Ip(x)dxl2EI(x)dx
例：试求图示悬臂梁的变形能，并利用功 能原理求自由端B的挠度。

结构力学稳定理论

结构力学稳定理论
1）3于结）当中论P体性：=系k平/l处，衡于当（稳θ临为定界任平状意衡态值状）时态这，时时Π，的恒其荷等总载于势称零能为(必即临为U界=最U荷小P载) 。。Pc体r=k系/l处。 2）临P<界Pc状r 态Π的能量特征是：P=势P能cr 为Π驻值δΠ=0 ，P且>P位cr移Π有非零
解。即在荷载达到临界值前后，总势能由正定过渡到非正定θ。 3）如以原始平衡位置作为参考状态，当体θ系处于中性平衡P=Pcr
时，必有总势能θ=0。对于多自由度体系，结论仍然成立。
2）能量法
•在新的平衡位 置各杆端的相 对水平位移
A
YA=Py1/l
y1
Bk
R1=ky1
y2
kC
R2=ky2
Dλ P YD=Py2/l
l
l
l cos
2l sin 2
2
1 2
l能①2量给法出12步新l(骤的ly )平:2 衡 形12 式yl 2 ;②写出
体系具有足够的应变能克服荷载势能，使压杆恢复到原有平
衡位置)当θ=0，Π为极小值0。
对于稳定平衡状态，真实的位移使Π为极小值
2）P>k/l ，当θ≠0，Π恒小于零（Π为负定） (即U<UP表示体系缺 少足够的应变能克服荷载势能，压杆不能恢复到原有位置) 。当 θ=0，Π为极大值0。原始的平衡状态是不稳定的。
对于具有n找个新自的由平度衡的位结置构，，列新平的衡平方衡程形，式需E要I=∞n个独立的位
l
移参数确定，由在此新求的临平界衡荷形载式。下也可列出n个独立的平衡方程，
它们是以n个独立的位移参数为未知量的齐次代数方θ程组。根据
临P(l界Pl状Mkk态)A的静00 力θ特=0征，，原该始齐平次衡方程组除零解转外动（刚对应于原有平

结构力学结构弹性

结构力学结构弹性

k1 1
M Fy k11
， 令 n2 F
上式可写为
EI
y"n2 y n2 k11
F
微分方程的通解（挠曲线方程）
y Acosnx B sin nx k11
F
式中，A，B为任意常数。挠曲线的边界条件为
当 x=0 时，y=0， y′= 1 当 x=l 时，y k11
F
δF
y
y 1
k1
δ
y y 1
k1
F
B
EI
l x A
F
M
y
x
y 1
A
k1 1
F k11 0
k11
F
\
1.弹性支座（弹性）压杆的稳定
δF
取下段隔离体分析，由M A 0 有
B
F
M
EI
y
因 EIy" M 于是可得挠曲线微分方程
y
l
x
x
y 1
A
EIy" Fy k11
或
y" F y k11
EI EI
y 1
A
k1
F2=0.382kl 时，失稳形式是 因 F2 <F1，所以临界荷载为 而真正的失稳形式是
y2 F1 kl 0.618
y1
F1
y2 F2 kl 1.618
y1
F2
Fcr F2 0.382 kl y2 1.618 y1
2. 弹性压杆（无限自由度）的临界荷载
图示一段固定另一端铰支的等 截面弹性压杆。设失稳时杆件 的挠曲线为 y=y(x)，C为任一 截面，其弯矩为M，取AC段 分析，
(1) 按小变形分析
由于位移和变形都很小，近似地取 sin ，则平衡方程

材料力学13能量法

材料力学13能量法
FN (x)
T (x)
M (x)
FN (x)
T (x)Fs(x)
Vε
FN2 (x) dx l 2EA(x)
T 2(x) dx l 2GIp (x)
M 2(x) dx l 2EI (x)
kFs 2 (x) dx l 2GA(x)
对若k于是杆双用件向来及弯修杆曲正系，横的弯力变矩弯形沿曲是形时以心切弯主应曲轴力变分不形解沿为, 截主面的均，匀因分轴布力的和修剪正力系远数小，
)
再施加P1
AB又伸长
Dl AB

P1l1 EA
P2保持不变，作功为
V 2

P2

P1l1 EA
P1作功为
V 3

P12l1 2EA
（5）应变能是可逆的。(跳板跳水) 总功仍为上述表达式。10
直接利用功能原理求位移的实例 利用能量法求解时，所列
例 求简支梁外力P作用点C的挠度。 弯矩方程应便于求解。
V F

FL3 48 EI
wC
29
说明： （1）卡氏第二定理只适用于线性弹性体
δi

Vε Fi
（2）Fi 为广义力，i为相应的位移
一个力
一个力偶
一对力
一对力偶
一个线位移
一个角位移
相对线位移
相对角位移
30
（3）卡氏第二定理的应用
（a） 轴向拉伸与压缩
δi

Vε Fi

Fi
22
F
B2
wC1
解：由功的互等定理 F wC1 M B2
得：F

wC1

M
Fl 2 16EI

材料力学-13 能量法共36页文档

材料力学-13 能量法共36页文档

RA
2a
a
1/2
2a
a
【解】
RA
qa 2
1 RA 2
（1）求截面的挠度（在 c 处加一单位力“1”）
AB:
M(x1)
q2ax1
qx12 2
M
(
x1
)
x1 2
河南理工大学力学系
材料力学
q
A
RA
2a
F=qa
B
CA
x2
a
1/2
第十三章 能量法
1
B
C
x2
2a
a
BC:
M(x1)q2ax1
qx12 2
M(
x1 )
§13-2 杆件变形能的计算
一、变形能的计算
拉压变形能 扭转变形能
V
FN2l 2EA
T 2l V 2GI p
河南理工大学力学系
材料力学
第十三章 能量法
弯曲变形能
Me
1. 纯弯曲
θ
Me
Me
Me
V W 1 2M eθ1 2M eM E el IM 2E e2lI
2. 横力弯曲
V
Me2(x)dx l 2EI(x)
河南理工大学力学系
材料力学
第十三章 能量法
例题13-2 图示为一水平面内的曲杆，B 处为一刚性 节点, ABC=90°在 C 处承受竖直力 F，设两杆的抗弯刚 度和抗扭刚度分别是 EI 和 GIp ，求 C 点竖向的位移。
F
A a
C Bb
河南理工大学力学系
材料力学
F
C
A
x1
x2 B b a
【解】在 C点加竖向单位力
V L 2EI dx
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

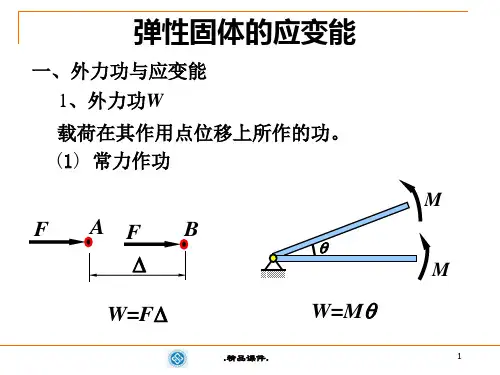
三 利用功能原理计算位移
第十三章 能量法/三 利用功能原理计算位移
利用
U W
1 P 2
可以计算荷载作用点的位移,但是
只限于单一荷载作用,而且所求位移只是荷载作用点 (或作用面)沿着荷载作用方向与荷载相对应的位移。
第十三章 能量法/三 利用功能原理计算位移
例题 图示变截面受拉杆，E、A 为已知，求加力点C的水平位
第十三章 能量法/二 变形能
4 关于变形能计算的讨论
1 2 以上计算公式仅适用于线弹性材料在小变形下的变形能的计算。 变形能可以通过外力功计算，也可以通过杆件微段上的内力功
等于微段的变形能，然后积分求得整个杆件上的变形能。
3 变形能为内力（或外力）的二次函数，故叠加原理在变形能计算
中不能使用。只有当杆件上任一载荷在其他载荷引起的位移上不做功
P
CP
Pl 3 48 EI
BP
mo
Pl 2 16 EI
A
B
Bm
o
C
Cm
o
mol 2 16 EI
mol 3EI
L/2
L/2
B
Pl 2 16 EI
Pl 3 mo l 2 C 48EI 16 EI

mo l 3EI
第十三章 能量法 /一 外力功
解: (2)外力功的计算
FN L U W 2 EA
式中
2
FN
——轴力，
A ——截面面积
第十三章 能量法/二 变形能
由拉压杆件组成的杆系的变形能： 2 1 5 4 受力复杂杆(轴力沿杆的轴线变化)的变形能
x
P 3
2 n Pi 2 Li FNi Li U i 1 2 Ei Ai i 1 2 Ei Ai n
应的位移上所作的功全部以能量的形式储存在弹性体 内，这种因变形而储存的能量称为变形能。
第十三章 能量法/二 变形能
1 变形能、功能原理 定义：功能原理
外力功等于变形能（能量守恒及转换原理）
U W
第十三章 能量法/二 变形能
2、杆件产生基本变形时的变形能
（1）轴向拉伸或压缩
P A L L P L o B
dx
q L
FN ( x)dx U dU L L 2 EA
2
第十三章 能量法/二 变形能
（2）圆截面杆的扭转 m m m
A

L o
圆截面杆的变形能
2 Mn L 1 U W m 2 2GI p
B
式中 Mn——圆杆横截面上的扭矩； I ——圆杆横截面对圆心的极惯性矩。
p
U dU U U dPi P i
(a)
第十三章 能量法/四 求位移的卡氏定理 (2) 先加 dP ，然后再加 P , P2 ,, Pn ，此时弹性体的变形能 1 i
由三部分组成： (a) dP 在相应的位移 d i 上所作的功 i (b) P , P2 ,, Pn 在相应位移 1
一般实心截面的细长梁:剪切变形能远小于其弯曲变形 能，通常忽略不计。
第十三章 能量法/二 变形能
3 产生组合变形时的变形能
M (x) M (x)
Mn
FN
Mn
FN
L
M 2 ( x)dx FN2 ( x)dx M n2 ( x)dx U L L L 2 EA 2GI p 2 EI
注意：变形能为内力（或外力）的二次函数，故叠加原 理在变形能计算中不能使用。
2 若在该杆上作用的外力多于一个,如在b截面上还作 用一个P1力,这时.外力表达式无两个或两个以上的位
移,显然也不能求位移的大小。
第十三章 能量法
四 求位移的卡氏定理
第十三章 能量法/四 求位移的卡氏定理
1 卡式定理
若弹性体上作用着多个外力(广义力),则该弹性
体的变形能 U(P1, P2, Pn) ,对于任一外力的偏导数, 就等于该力作用处沿其作用方向的位移(广义位移), 即
2
第十三章 能量法/一 外力功 ·计算
分析与讨论
若先加mo ，后加P ，则外力功为
1 1 W2 mo Bmo mo BP P cp 2 2 mol 1 Pl 2 1 Pl 3 mo mo P 2 3EI 16 EI 2 48EI mo l Pmol 2 P 2l 3 6 EI 16 EI 96 EI
2
第十三章 能量法/一 外力功 ·计算
分析与讨论
比较计算结果，说明：
W W1 W2
即作用在弹性体上的所有外力作的总功W,等于这些力分别
与其相应位移乘积之和的一半。而与各个力的施加次序无
关。
第十三章 能量法
二 变形能
第十三章 能量法/二 变形能
1 变形能、功能原理 定义：变形能
当弹性体受到外力作用而发生变形时，外力在相
结构力学
第十Hale Waihona Puke 章 能量法第十三章 能量法
利用功能原理解决工程结构位移或杆 件变形等有关问题的方法,称为能量法
第十三章 能量法
一 外力功 二 变形能
三 利用功能原理计算位移
四 求位移的卡氏定理
第十三章 能量法
一 外力功
第十三章 能量法 /一 外力功
定义:
任何弹性体在外力作用下都要发生变
形。弹性体在变形过程中,外力沿其作用线
U P n
1
P1 2
P2
Pi
i
Pn
n
第十三章 能量法/四 求位移的卡氏定理
证明： 考虑两种不同的加载次序。 (1)先加 P , P2 ,, Pn ，此时弹性体的变形能为U： 1
U f ( P , P2 ,, Pn ) 1
再加增量 dP，则变形能U的增量dU为 i U dU dPi Pi 梁的总变形能为：
第十三章 能量法/二 变形能
受力复杂的圆截面杆(扭矩沿杆的轴线为变量)
2 M n ( x)dx U dU L L 2GI p
t
A x L
dx
B
第十三章 能量法/二 变形能
（3）平面弯曲
m
m
A o B
L
纯弯曲梁的变形能：
m
1 M 2L U W m 2 2 EI
式中 M－梁横截面上的弯矩； I－梁横截面对中性轴的惯性矩
分析与讨论
若先加P，后加mo，则外力功为
1 1 W1 P cP P cmo mo Bmo 2 2 mol 2 ml 1 Pl 3 1 P P mo o 2 48EI 16 EI 2 3EI Pmol 2 m l P 2l 3 o 96 EI 16 EI 6 EI
3、多个力作用下的外力功
1
P1 2
P2
Pi
i
Pn
n
外力功的最终值仅与各个外力的最终值有关,
而与各个力的施加次序无关
第十三章 能量法 /一 外力功
例题:计算图示简支梁上的外力功
P mo A EI L/2 B C EI
L/2
第十三章 能量法 /一 外力功
解:(1)位移计算 梁在P和mo共同作用下C 截面的位移 c 和B截面的转角 B ：
第十三章 能量法/三 利用功能原理计算位移
（2）位移计算
1 U W P cx 2
即
1 3P 2 l P cx 2 4 EA
得
3P l cx 2 EA
第十三章 能量法/三 利用功能原理计算位移
分析和讨论 1 若需要位移处无外力作用,如求b截面 bx ,外力功表
达式中无需求的位移项,因此无法求 bx 。
移
cx
P
2A
a l b
A
c l
第十三章 能量法/三 利用功能原理计算位移
解：（1）变形能计算
U ab
l
0
P 2 dx P 2l 2 E (2 A) 4 EA
2l
U bc
l
P 2 dx P 2l 2 E ( A) 2 EA
整根杆的变形能
3P 2 l U ab U bc 4 EA
分析与讨论
(2)为什么有时两种荷载单独作用时的变形能可以进行
叠加,是因为其中一种荷载在另一种荷载引起的位移上不作 功. 例如,一直杆同时承受弯曲与扭转作用时,就可以把扭 转变形能和弯曲变形能叠加起来进行计算.因为扭转在弯曲
引起的转角 上不作功,弯矩在扭转引起的扭转角 上也
不作功.
第十三章 能量法
l
第十三章 能量法/二 变形能
例题 计算图示梁在集中力P作用下的变形能
EI
(b) A
P
l
x
B
M (2x)dx Ub U p 0 2 EI
l
( Px)2 dx P 2l 3 0 2EI 6EI
l
第十三章 能量法/二 变形能
例题 计算图示梁在集中力偶mo、集中力P共同作用下的变形能
1 1 W P P c 2 2 mol 2 1 Pl 3 P( ) 2 48EI 16 EI Pmol 2 m l P 2l 3 o 96 EI 16 EI 6 EI
2
1 mo B 2 ml 1 Pl 2 mo ( o ) 2 16 EI 3EI
第十三章 能量法 /一 外力功
第十三章 能量法/二 变形能
横力弯曲梁(弯矩沿梁的轴线为变量)的变形能
U dU
L
M 2 ( x)dx 2 EI
P
L
m=Pa
A
a
B
a
C
第十三章 能量法/二 变形能
（4）剪切
U dU k
L L