当前位置：文档之家 › 自动控制原理 第五章(第四和五次)

自动控制原理 第五章(第四和五次)

  • 格式：ppt
  • 大小：2.07 MB
  • 文档页数：46

下载文档原格式

  / 46

合集下载

自动控制原理 自控第五章

自动控制原理 自控第五章

【授课时间】：2013.11.18、11.20上午三四节【授课形式】：多媒体 【授课地点】：4306 4114 【授课时数】：2 【授课题目】：频率特性及典型环节的频率特性 【教学目标】1、正确理解频率特性的概念；2、熟练掌握典型环节的频率特性，熟记其幅相特性曲线及对数频率特性曲线。

【教学重难点】重点：典型环节的频率特性难点：典型环节的幅相特性曲线及对数频率特性曲线【教学内容】复数的表示形式： (1) 代数式：A =a +bj (2) 三角式：A =R (cos φ+j sin φ) (3) 指数式：A =Re j φ (4) 极坐标式：A =R ∠φ 5.1 频率特性 一、频率特性定义频率特性是控制系统在频域中的一种数学模型，是研究自动控制系统的一种工程求解方法。

系统频率特性能间接地揭示系统的动态特性和稳态特性，可简单迅速地判断某些环节或参数对系统性能的影响，指出系统改进方向。

频率特性的定义（1）频率响应: 在正弦输入作用下，系统输出的稳态值称为频率响应。

（2）频率特性: 频率响应c(t)与输入正弦函数r(t)的复数比。

()()()()()()j Q P e A A j j R j C j ωωωωϕωωωωωϕ+==∠=Φ=)()()(⎪⎪⎩⎪⎪⎨⎧=∠=Φ∠==Φ)()()()()()()()(ωϕωωωωωωωj R j C j A j R j C j()|()|A G j ωω==幅频特性：输出响应中与输入同频率的谐波分量与谐波输入的幅值之比A(ω)为幅频特性相频特性： 输出响应中与输入同频率的谐波分量与谐波输入的相位之差φ(ω)为相频特性实频特性： 虚频特性： 例5-1 已知u i (t )=A ·sin ωt 。

()()()t u t u dt t du RC r C C =+()()11+=Ts s U s U i C 其中，T =RC ()22ωω+=s A s U i()()22221111ωωωω+⎪⎭⎫ ⎝⎛+⋅=+⋅+=s T s T A s A Ts s U C零初始条件())arctan sin(112222T tT Ae AT uT tt c ωωωωτω-+++=-()()()()ωϕωωωωω+∙=-+=t A A T t TA t u s c sin )arctan sin(122上式表明：对于正弦输入，其输出的稳态响应仍然是一个同频率正弦信号。

《自动控制原理》胡寿松自动控制原理简明教程第5章详解

《自动控制原理》胡寿松自动控制原理简明教程第5章详解

bm1s bm an1s an
➢ 惯性环节：1/(Ts+1)，式中T>0
➢ 一阶微分环节：(Ts+1)，式中T>0
➢ 积分环节：1/s
➢ 微分环节：s
➢ 振荡环节：1/[(s/ωn)2+2ξs/ωn+1]；式中ωn>0，0 < ξ <1 ➢ 二阶微分环节：(s/ωn)2+2 ξ s/ωn+1；式中ωn>0，0 < ξ <1
线性分度，单位是分贝（dB）；对数相频曲线的纵坐标按 φ(ω) 线性分度，单位是度（°）。由此构成的坐标系称为 半对数坐标系。
ω和lgω的关系表
① ω轴为对数分度， 即采 用相等的距离代表相等的 频率倍增，在伯德图中横 坐标按μ=lgω均匀分度。 ② ω=0在对数分度的坐标系中的负无穷远处，ω =0不可能 在横坐标上表示出来，横坐标上表示的最低频率由所感兴 趣的频率范围确定。 ③ 从表中可以看出，ω的数值每变化10倍， 在对数坐标 上lgω相应变化一个单位。 频率变化10倍的一段对数刻度 称为“十倍频程”， 用“dec”表示。
arctg
2
曲线起自幅角
为－v90°的
无穷远处。
1. 极坐标图的起点
2T T 2
2
tan
1
2T T 2 2
1
0 L 0dB
-40
0 90
0
180
L 20 lgT 2 40 lgT
180
n
1 T
90
1 10 TT
40dB dec
(a) (b)
➢ 延迟环节
Gs eTs
G j e jT G j 1 G j T
精确曲线

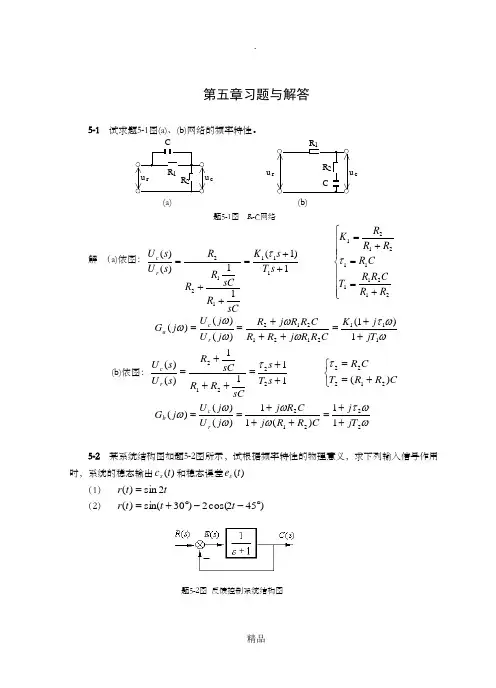
自动控制原理第五章习题及答案

自动控制原理第五章习题及答案

第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。

u r R1u cR2CR2R1u r u c(a) (b)题5-1图R-C网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图：⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++==5-2某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs和稳态误差)(tes（1）tt r2sin)(=（2）)452cos(2)30sin()(︒--︒+=ttt r题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ（2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ )]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应h t e e t tt ()..=-+≥--11808049试求系统频率特性。

《自动控制原理》5章课后习题参考答案.

《自动控制原理》5章课后习题参考答案.
G S S S =
+
1(
10000(6
.311
2e +=
S S S G
1001.0(11.0(1(1.0(d +++=
S S S S S G 61
.054
.0154.0,
11(2
2
=+==+=
K K
A ω
ωω010
s
900.257.3180 2.16rad
tg ωωω----∙︒=-=,(
(
5
.1,
(5
(6 (7
5.12
K增大和T减少
((1(1(1m K
K s s Ts Ts K
s T s K
Φ=
≈
+++++
K
T m 21=
ζ ,不变(稳定裕度不变
2
22
(12(121b n ωωξξ=-+
-+
5.13
11=+=
p
ssr K e 35
.01
12
416==
=
v
ssr K e %
8.4%100%2
1=⨯=--ξ
πξ
σe 05
.006.13
==≈
ቤተ መጻሕፍቲ ባይዱεξ
ω,S t n s s
rad n n c 8.2707.0707.02=∙=ωωω=0
63
=γdB K g s rad g ∞=∞=ω0,1==r r M ωs
rad n b 4==ωω0
1
1
11006
.787.53.841001.01001.0180180=-=∙-=-+-=----tg

自动控制原理第五章

自动控制原理第五章

1第五章 频域分析法目的：①直观，对高频干扰的抑制能力。

对快(高频)、慢(低频)信号的跟踪能力。

②便于系统的分析与设计。

③易于用实验法定传函。

§5.1 频率特性一. 定义)()()()(1n p s p s s s G +⋅⋅⋅+=θ在系统输入端加一个正弦信号：t R t r m ωsin )(⋅=))(()(22ωωωωωj s j s R s R s R m m -+⋅=+⋅=↔ 系统输出：))(()()()()(1ωωωθj s j s R p s p s s s Y m n -+⋅⋅+⋅⋅⋅+=2t j t j e A e A t y t y ωω⋅+⋅+=↔-瞬态响应)()(1 若系统稳定，即)(s G 的极点全位于s 左半平面，则 0)(l i m 1=∞→t y t 稳态响应为：t j t j ss e A eA t y ωω⋅+⋅=-)( 而)(21)()(22ωωωωωj G R j j s s R s G A m j s m -⋅-=+⋅+⋅⋅=-= )(21)()(22ωωωωωj G R jj s s R s G A m j s m ⋅=-⋅+⋅⋅== ∴t j m t j m ss e j G R je j G R j t y ωωωω⋅⋅+⋅-⋅-=-)(21)(21)( =])()([21t j t j m e j G e j G R jωωωω-⋅--⋅⋅ 又)(s G 为s 的有理函数，故)()(*ωωj G j G -=，即3φωωj e j G j G )()(=φωωj e j G j G -=-)()( ∴][)(21)()()(φωφωω+-+--⋅=t j t j m ss e e j G R jt y =)sin()(φωω+⋅⋅t j G R m=)sin(φω+⋅t Y m可见：对稳定的线性定常系统，加入一个正弦信号，其稳态响应也是一个同频率的正弦信号。

自动控制原理第五章

自动控制原理第五章

KT j 1 2T 2
0 : U(0) K
V (0) 0
1: T
:
U(1) K T2
U() 0
V(1) K T2
V() 0
●
●
K
●
0.707K
V(ω)
K/2 K
●
●
U(ω)
-K/2
●
10
3 由零、极点分布图绘制
1)在[s]上标出开环零极点；
G( j ) K K / T 1 jT j 1 / T
低频段 1
T
L( ) 20lg A( ) 20lg () arctgT 0
10
高频段
1
T
20lg A() 20lgT ( ) arctgT 900
转折频率 1
T
20lg A( ) 20lg 2 3.01 0db
( ) arctgT 450
15
20 0 -20 -40 -60 90 45 0 -45 -90
3) 振荡环节
1
G(s) (s / n )2 2 (s / n ) 1
n
1 T
0
4) 一阶微分 G(s) Ts 1 (T>0)
0 1
5) 二阶微分 G(s) (s / n )2 2 (s / n ) 1 (n 0, 0 1)
6) 纯滞后环节 G(s) e s
19
5-3-2 最小相位典型环节的频率特性
0.01
0.1
T
10
T
●
●
●
●
0.1
1/T1
10
T 0.1 () arctg0.1 5.70
T 1 ( ) arctg10 84.30

《自动控制原理》第五章：系统稳定性

《自动控制原理》第五章：系统稳定性

5.2 稳定的条件
当σi和λi均为负数，即特征根的 σi和λi均为负数， 均为负数 实部为负数，系统是稳定的； 实部为负数，系统是稳定的； 或极点均在左平面。 或极点均在左平面。
5.3 代数稳定性判据
定常线性系统稳定的充要条件 定常线性系统稳定的充要条件是特征方程的根具有负 充要条件是特征方程的根具有负 实部。因此，判别其稳定性，要解系统特征方程的根。为 实部。因此，判别其稳定性，要解系统特征方程的根。 避开对特征方程的直接求解，可讨论特征根的分布， 避开对特征方程的直接求解，可讨论特征根的分布，看其 是否全部具有负实部，并以此来判别系统的稳定性，这样 是否全部具有负实部，并以此来判别系统的稳定性， 也就产生了一系列稳定性判据。 也就产生了一系列稳定性判据。 其中最主要是E.J.Routh(1877 )h和Hurwitz（ 其中最主要是E.J.Routh(1877年)h和Hurwitz（1895 E.J.Routh(1877年 年）分别提出的代数判据。 分别提出的代数判据 代数判据。
习题讲解： 习题讲解：
µ
G1
Q21
G1
h2
k1 k1 G1 ( s ) = , G1 ( s ) = (T1s + 1) (T1s + 1) k1k 2 G0 ( s ) = (T1s + 1)(T2 s + 1)
kp
G0 ( s ) G(s) = 1 + G0 ( s ) K p
5.4 Nyquist稳定性判据 Nyquist稳定性判据
系统稳定的条件？ 系统稳定的条件？
5.2 稳定的条件
d n y (t ) d ( n −1) y (t ) dy (t ) 线性系统微分方程： 线性系统微分方程： n a + an −1 + L + a1 + a0 y (t ) n ( n −1) dt dt dt d m x(t ) d ( m −1) x(t ) dx(t ) = bm + bm−1 + L + b1 + b0 x(t ) m ( m −1) dt dt dt d n y (t ) d ( n −1) y (t ) dy (t ) + a( n −1) + L + a1 + a0 y (t ) = 0 齐次微分方程： 齐次微分方程： an n ( n −1) dt dt dt an s n + an −1s n −1 + L + a1s + a0 = 0 设系统k 设系统k个实根

自动控制原理 第五章 频率法

自动控制原理 第五章 频率法

频率特性
在稳态下输出：e2 = E2Sin(wt +υ ) 仍是正弦信号, 频率不变, 幅值和相角发生变化. 变化与w有关. 1/jwC 1 写成矢量形式：e2 = ————— e1 = ———— e1 R + 1/jwC 1+jwRC e2 1
-— = ———— e1 1+jwRC
与电路参数RC有关、与输入电压的频率有关
自动控制原理
蒋大明
幅相特性与传递函数之间的关系
输出输入的振幅比（幅频特性）： A(w) = Ac/Ar = | G(jw)| = G(S) | 输出输入的相位差（相频特性）： υ (w) = υ - 0 =∠G(jw) =∠G(S) | 所以：G(jw) = G(S)|S=jw 频率特性 传递函数 证毕
自动控制原理
蒋大明
一阶不稳定环节
一阶不稳定环节的对数幅频特性与惯性环节的完全一样；相频则有所 不同，是在-180至-90范围内变化.
L ( )
0 -20
1
10

(a )
( )
0o
90o

(b)
180o
图5-20 一阶不稳定环节 的对数频率特性
自动控制原理
蒋大明
时滞环节
传递函数： G(S) = e-τ
S
幅相频率特性：
G(jw) = e-jτ
A(w) = 1 υ (w) = -τ w
w
自动控制原理
蒋大明
时滞环节
对数频率特性： L(w) = 20 lg A(w) = 20lg 1 = 0 υ (w) = -τ w
（横坐标对数分度，曲线）
自动控制原理
蒋大明
第三节
1.

自动控制原理(胡寿松版)完整第五章ppt课件

自动控制原理(胡寿松版)完整第五章ppt课件

-20
φ (ω )
ω=0.1 L(ω )=20lg0.1=-20dB 90
对数相频特性：φ (ω )=90o 0 0.1
1
10ω
第二节 典型环节与系统的频率特性
4)．惯性环节
G(s)=Ts1+1
G(ωj
)=
jω
1 T+1
(1) 奈氏图
A(ω
)=
1 1+(ω T)2
φ (ω )= -tg-ω1 T
取特可殊以点证：绘明ω制：=0奈氏图近似方I法m : AA图心半A点(ω(ω(是 ， 圆ω，))=以 以 。惯=)0然=根ωω0(1性.171==/后据0/环2∞27为T将幅1节φ,jφo半φ它频的(ω)(ω径为(ω奈们特))=的圆)=氏平-性=09-o0滑4和o5连o相ω接频起∞特来0性-。求45ω=出T1特殊ω1=0Re
5）二阶微分环节 s 2 /n 2 2s /n 1(n 0 ,0 1 )
6）积分环节 1 / s
7）微分环节 s
第二节 典型环节与系统的频率特性
（2）非最小相位系统环节
1）比例环节 K (K0)
2）惯性环节 1/( T s1 ) (T0) 3）一阶微分环节 Ts1 (T0)
4）振荡环节 1 /( s 2 /n 2 2 s /n 1 )(n 0 ,0 1 )
第一节 频率特性
系统输入输出曲线 定义频率特性为:
r(t) c(t)
r(t)=Asinωt
G(ωj )
=|G(jω)|e j G(jω) =A(ω )e φj (ω )
A 0
幅频特性： t A(ω )=|G(jω)|
G(jω)
A G(jω )
相频特性： φ (ω )= G(jω)

自动控制原理第五章

自动控制原理第五章

L( )
Im
c
-1
1


0
ωc
(c )
Re
( )

90
180

2.增益裕度
定义：开环频率特性曲线相位为-π 时对应幅值的
倒数。
计算:
GM
1 1 1 , Kg Wk ( j ) A( j ) 1
或h 20 lg

20 lg
含义:
增益裕度含义
① 乃图上 WK ( j ) A( ) 1 的单位图对应于Bode图 的零分贝线。 ② 单位图以外对应L(ω )>0 ③ 乃图上负实轴对应于Bode图上相频特性的－π 线。
三、系统稳定裕度
稳定裕度：衡量闭环系统相对稳定性的指标。
相位裕度： 开环频率特性曲线上模值
等于1的矢量与负实轴的夹角。
增益裕度：开环频率特性曲线与负实轴相
交点模值的倒数。
1.相位裕度
定义：在频率特性上对应于幅值A(ω )＝1的角频
率称为剪切频率，用 ω c表示。在剪切频率ω c使系统 达到稳定的临界状态所要附加的相角迟后量，称为相 位裕度。
计算: 含义:
( c ) 180 ( c )
相位裕度含义
L( )
1.BODE图
-2
20 lg K
1
-1
10
c
20 lg h

( )
-3
90
180
270

2.稳定分析图
L( )
-2
20 lg K
1
-1
10
c
20 lg h

( )
-3

自动控制原理第五章频域分析法

自动控制原理第五章频域分析法
一 由传递函数求系统的频率响应
第19页/共187页
频率特性
对应的幅值和相角：
同理，可求得对应于2的|G(j2)|和(j2) 。
若对取所有可能的值，则可得到一系列相应的幅值和相位。 其中幅值随频率变化而变化的特性称为系统的幅频特性。 相角随频率变化而变化的特性称为系统的相频特性。
第20页/共187页
每当ω增加十倍， L(ω)减少20dB负20分贝十倍频程 －20dB/ dec
第34页/共187页
5－3典型环节和开环系统频率特性
第35页/共187页
积分环节L(ω)
[-20]
[-20]
[-20]
第36页/共187页
5－3典型环节和开环系统频率特性
三、微分环节
幅频特性与ω成正比，相频特性恒为90°
第12页/共187页
5-2频率特性
以RC网络为例，说明频率特性的基本概念。
取拉氏变换，求网络的传递函数
如果输入为正弦量：
由电路分析，电路达到稳态时，输出也是以ω为角频率的正弦量。
在传递函数中G(s)中，只要令s=jω，则可由⑴式得到⑵式。
第13页/共187页
5-2频率特性
控制系统的三种数学模型：微分方程、传递函数、频率特性可以相互转换，它们的关系见右图。
交接频率将近似对数幅频特性曲线分为二段：低频段和高频段。
第41页/共187页
惯性环节G(jω)
φ(ω) = -tg-10.5 ω
ω
0
0.5
1
2
4
5
8
20
φo(ω)
A(ω)
0
1
-14.5
0.97
-26.6
0.89

自动控制原理第5章

自动控制原理第5章

自动控制原理
第五章 频域分析法－频率法
1 sin(t arctanT ) 1 2T 2
1
e jarctanT
j 1
e 1 jT
1 2T 2
jT
1
1 jT
RC网络的频率特性
只要把传递函数式中的s以j置换，就可以 得到频率特性，即
1
1
1 jT 1 Ts sj
自动控制原理
第五章 频域分析法－频率法
对数相频特性：( ) arctan 特征点： 1 , L( ) 3dB, 45
自动控制原理
第五章 频域分析法－频率法
一阶微分环节的伯德图 幅相曲线
自动控制原理
第五章 频域分析法－频率法
六、振荡环节
传递函数： 频率特性：
G(s)
2 n
s2 2n s n2
1
s
n
2
2 n
s1
G( j
M ( ) G(j )
G1(j ) G2 (j ) G3(j ) M1( ) M2 ( ) M3 ( )
( ) G(j ) G1(j ) G2(j ) G3(j ) 1( ) 2( ) 3( )
自动控制原理
第五章 频域分析法－频率法
1.开环幅相特性曲线的绘制
例 某0型单位负反馈控制系统，系统开环
频率特性： G(j) 2 j 2 2 j 1
对数幅频特性：
L() 20lg G j 20lg 1 22 2 2 2
对数相频特性：
arctan
1
2 2
2
自动控制原理
第五章 频域分析法－频率法
幅相曲线: 0时，M 1, 0 ; 时，M =, =180
自动控制原理

自动控制原理课件第五章

自动控制原理课件第五章

1 幅相频率特性
• • •
曲线或极坐标图。 在复平面，把频率特性的模和角同时表示出来的图就是 幅相曲线或极坐标图。 它是以 为参变量，以复平面上的矢量 G ( j ) 表示的一 种方法。 例 惯性环节幅相频率特性
G ( j ) k 1 jT k 1 T
2 2
•幅相频率特性曲线：又称奈奎斯特（Nyquist）
模从- 相角从-/2-3/2
-1
Im
ω
∞
Re
ω ω
0
系统开环对数频率特性例题2
系统开环对数频率特性
系统开环对数频率特性例题3
系统开环传函：
G (s)
-1 -1 0.05 0.1 1 2 10 100 -2 -90°
20 lg 40 20 lg 1 0 . 05 20 lg
L( )
为横坐标，
为纵坐标。
5-3 典型环节及开环频率特性 一、典型环节的频率特性p177
•要求掌握以下各环节幅相频率特性及对数频率 特性。
比例环节、微分环节、 积分环节、 惯性环 节、 振荡环节、 一阶微分环节、 二阶微分 环节、 延时环节。 非最小相位环节 开环传函中包含右半平 面 的零点或极点。
比例 G( s ) k , G( j ) k , 积分 ( s ) , G ( j ) G , s j 微分
1 1
k, 0
1


, 90

G( s ) s, G( j ) j ,
, 90

惯性环节（对比一阶微分环节）
G( s) 1 Ts 1 1 1 T
s
G ( j ) e
j
cos j sin

05_自动控制原理—第五章(4)讲解

05_自动控制原理—第五章(4)讲解
当系统开环频率特性曲线及其镜像通过(-1，j0)点时，表明在s平面 虚轴上有闭环极点,系统处于临界稳定状态，属于不稳定。
例5-3 一个闭环系统如图所示。其开环 传递函数为
G(s)=K/(Ts-1),K＞1 这是一个不稳定的惯性环节,开环特征 方程式在右半s平面有一个根,P=1。闭 环传递函数为
(s)=K/(Ts+K-1) 由于K＞1,闭环特征方程式的根在左半s 平面,所以利用代数方法可以判断闭环 是稳定的。
特别是，如果知道了开环特性，要研究闭环系统的稳定性， 还需要求出闭环特征方程，无法直接利用开环特性判断闭环系统 的稳定性。而对于一个自动控制系统，其开环数学模型易于获取， 同时它包含了闭环系统所有环节的动态结构和参数。
除劳斯判据外，分析系统稳定性的另一种常用判据为 奈奎斯特（Nyquist）判据。Nyquist稳定判据是奈奎斯 特于1932年提出的，它是频率法的重要内容，简称奈氏 判据。奈氏判据的主要特点有
1. 只绘制由0变到+ 时的开环幅相频率特性G(j)
因为（0，+∞）与（-∞，0）的曲线完全关于实轴对称，则0变到
+ 时的开环幅相频率特性G(j)顺时针包围(-1,j0)点的圈数N’满
足
N’= N/2 N是当从-∞变化到+∞时，系统开环频率特性曲线及其镜像G(j)
顺时针包围(-1,j0)点的圈数。 因此，简化奈奎斯特稳定判据可改为
Z = N + P=2 Nˊ+P
2.采用穿越的概念简化复杂曲线包围次数的 计算
由0变到+ 时开环频率特性曲线要形成对 (-1,j0)点的一次包围，势必穿越（-∞，-1）区 间一次。
开环频率特性曲线逆时针穿越（-∞，-1）区 间时，随ω增加，频率特性的相角值增大，称为 一次正穿越N+。

《自动控制原理》 第五章习题解答

《自动控制原理》 第五章习题解答
胡寿松自动控制原理习题解答第五章
5-2 若系统单位阶跃响应为
h(t) = 1−1.8e −4t + 0.8e −9t
试确定系统的频率特性。 解：对单位阶跃响应取拉氏变换得：
1 − 1.8 + 0.8 =
36
s s + 4 s + 9 s(s + 4)(s + 9)
(t ≥ 0)
即： C(s) = G(s) =
K,T1,T2 > 0
当取ω = 1时， ∠G( jω ) = −1800 ， G( jω ) = 0.5 。当输入为单位速度信号时，系统的稳
态误差为 0.1，试写出系统开环频率特性表达式。
解： KV
= lim sG(s) = s→0
K
= 10
当ω = 1时 G( jω ) = K (T2ω )2 + 1 = 10 (T2 )2 + 1 = 0.5
T2
=
1 20
T1 = 20
T1
=
1 T2
代入到
G(
j)
=
10
(T2 )2 + 1 (T1 )2 + 1
=
0.5 中得到：
所以系统的开环传递函数为： G(s) = 10(−s / 20 + 1) s(20s + 1)
系统开环频率特性表达式为： G( jω ) = 10(− jω / 20 + 1) jω(20 jω + 1)
ω
2 n
=1
(ω
2 n
− 1)
+
(2ζω n )2
∠GB
(
jω
)
=
−
arctan
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6
5-5 频域稳定判据（奈氏判据）
自动控制原理
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
Im
K=100
P=0; R=-2;
Z=0-(-2)=2 闭环系统在 s 右半平面有两个 极点，系统不稳定
-1
+∞
ω=0
Re
闭环传递函数在复平面右半平面有Z个极点
Z PR
R(>0)为Nyquist曲线逆时针包围（-1，j0）点的圈数; R(<0)为Nyquist曲线顺时针包围（-1，j0）点的圈数;
➢只要在这个闭合曲线 内没有F(s)的零点，系 统即为稳定的。
+∞ Im ∞
O Re
-∞
3
5-5 频域稳定判据（奈氏判据）
自动控制原理
➢对于真有理分式，s等于无穷
大的时候，|G(s)H(s)|=0，在
+∞ Im
G(s)H(s)曲线中对应坐标原点。
∞
➢我们只需考察S在虚轴上取值
O
的情况
Re
➢ s j 在复平面上的
自动控制原理
(2)开环传递函数含ν 个积分环节 ν型系统
Ga (S )
K S (TS 1)
Im
-1
0
(a)ν=1,从 0 点逆时针
0 Re
补画半径为无穷大的1/4圆。
0
P=0, N=0，Z=0，
所以，闭环系统稳定。
22
5-5 频域稳定判据（奈氏判据）
自动控制原理
Im
0 -1 0
＝0
曲线G，( j就)是HN( jyq)uist曲线
-∞
4
5-5 频域稳定判据（奈氏判据）
自动控制原理
2. Nyquist稳定判据
如果系统的开环传递函数G(s)H(s)在右半平面有P个
极点，则闭环系统稳定的充分必要条件为：当ω从-∞
连续地变化到+∞时，开环频率特性G(jω)H(jω)的
Nyquist图逆时针方向包围复平面的-1点P圈。 Im
-1
0 (b) K Re
K Gb(S) (T1S 1)(T2S 1)(T3S 1)
P=0, NN N 011
闭环不系统稳定。 Z=P-2N=2
Im
0 0
K -1
Re
(c)
Gc
(S)
K (TS1)
P=1,
N
N
N
1 2
0
1 2
Z=P-2N=1-1=0
闭环系统稳定。
21
5-5 频域稳定判据（奈氏判据）
11
5-5 频域稳定判据（奈氏判据）
自动控制原理
例1.某最小相位系统的开环Nyqusit曲线如图所示 试确定其闭环系统的稳定性
N 1； N 1
Im
Z P 2N
C
P 2(N N ) -2
0 2(11)
0
B
A
-1.5 -1 0.5 0 Re
闭环系统稳定
12
5-5 频域稳定判据（奈氏判据）
33
5-5 频域稳定判据（奈氏判据）
自动控制原理
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
Im
K=100
P=0; R=-2;
Z=0-(-2)=2 闭环系统在 s 右半平面有两个 极点，系统不稳定
-1
+∞
ω=0
Re
闭环传递函数在复平面右半平面有Z个极点
Z PR
R(>0)为Nyquist曲线逆时针包围（-1，j0）点的圈数; R(<0)为Nyquist曲线顺时针包围（-1，j0）点的圈数;
19
5-5 频域稳定判据（奈氏判据）
自动控制原理
稳定性分析举例
(1)开环传递函数不含积分环节（0型系统）
Ga
(S)
(T1S
K 1)(T2S
1)
P=0, N=0 Z=P-2N=0 该闭环系统稳定。
Im
0 0
-1
K Re
（a）P＝0 奈氏曲线
20
5-5 频域稳定判据（奈氏判据）
自动控制原理
Im
0
➢只要在这个闭合曲线 内没有F(s)的零点，系 统即为稳定的。
+∞ Im ∞
O Re
-∞
30
5-5 频域稳定判据（奈氏判据）
自动控制原理
➢对于真有理分式，s等于无穷
大的时候，|G(s)H(s)|=0，在
+∞ Im
G(s)H(s)曲线中对应坐标原点。
∞
➢我们只需考察S在虚轴上取值
O
的情况
Re
➢
s j在复平面上的
➢1+G(s)H(s)曲线包围原点的圈数就是G(s)H(s)包围-1 点的圈数；
➢因此，闭环系统的稳定性可以通过研究开环传递函 数G(s)H(s)的曲线包围复平面上-1点的圈数来判断， 而无需画1+G(s)H(s)的曲线
2
5-5 频域稳定判据（奈氏判据）
自动控制原理
(3)复平面上闭合曲线的选择
➢选择闭合曲线包围复 平面的右半部
Re
Gb (S)
S
2
K (TS
1)
(b)由于ν＝2，从 0点逆时针 补画半径为无穷大的半园。 P=0, N=-1，Z=2 该闭环系统不稳定。
23
5-5 频域稳定判据（奈氏判据）
自动控制原理
0 Im
10 Gc (S) S(TS 1)
0
(c)ν=1,从 0 点逆时针
＝0
ReLeabharlann 补画半径为无穷大的1/4圆。
P为开环传递函数在S右半平面的极点个数
Z P 2N
10
5-5 频域稳定判据（奈氏判据）
自动控制原理
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
N 0； N 1
Im K=100
-1
+∞
ω=0
Re
Z P 2N P 2( N N ) 0 2(0 1) 2
闭环系统不稳定
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1) -1
K=20
_+∞∞
ω=0
Re
32
5-5 频域稳定判据（奈氏判据）
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
-1
K=20
自动控制原理
Im
_∞
+∞
Re
ω=0
G( j) a() jb() G( j) e j () c() jd ()
R=P-Z
其中：R为圈数，正表示逆时针方向：负表示顺时针 方向。
28
5-5 频域稳定判据（奈氏判据）
自动控制原理
(2)F(s)有理分式函数的选择
F(s) 1 G(s)H (s)
1 B(s) A(s) B(s)
A(s)
A(s)
F(s)的零点为闭环传递函数的极点，F(s)的极点为开
环传递函数的极点。
(
arctgx
)
0
dx
x2
( arctg 3) 1.21
3
27
5-5 频域稳定判据（奈氏判据）
自动控制原理
1. 奈氏判据的数学基础
设s为复变量，F(s)为有理分式函数
(1)幅角原理：
设在s平面上任一闭合曲线包围了F(s)的Z个零点 和P个极点，并且不经过F(s)的任一零点和极点，则 当s沿闭合曲线顺时针方向旋转一圈时，映射到F(s) 平面内的F(s)曲线逆时针绕原点（ P–Z ）圈。即
7
5-5 频域稳定判据（奈氏判据）
自动控制原理
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
Z PR
R的确定方法
Im K=100
-1
+∞
ω=0
Re
G(jω)H(jω)曲线包围(-1,j0)点的圈数，仅仅与幅相曲线 穿越实轴区间(-,-1)的次数有关。
根据对称性，只需考察 0 时的情况
解：
自动控制原理
P194 例5-9
2
(x ) x arctgx (2k 1) k 0,1, 2,.....
( arctgx ) / x 取k 0
26
5-5 频域稳定判据（奈氏判据）
A(x )
2 1
1 x2
x 3
自动控制原理
( arctgx ) x
减函数
d
(0
x 1 x2
)
➢1+G(s)H(s)曲线包围原点的圈数就是G(s)H(s)包围-1 点的圈数；
➢因此，闭环系统的稳定性可以通过研究开环传递函 数G(s)H(s)的曲线包围复平面上-1点的圈数来判断， 而无需画1+G(s)H(s)的曲线
29
5-5 频域稳定判据（奈氏判据）
自动控制原理
(3)复平面上闭合曲线的选择
➢选择闭合曲线包围复 平面的右半部
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1) -1
K=20
_+∞∞
ω=0
Re
5
5-5 频域稳定判据（奈氏判据）
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
-1
K=20
自动控制原理
Im
_∞
+∞
Re
ω=0
G( j) a() jb() G( j) e j () c() jd ()
5-5 频域稳定判据（奈氏判据）