当前位置：文档之家 › 自动控制原理作业参考答案(第五章

自动控制原理作业参考答案(第五章

  • 格式：doc
  • 大小：297.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

自动控制原理 第五章(第四和五次)

自动控制原理 第五章(第四和五次)

6
5-5 频域稳定判据（奈氏判据）
自动控制原理
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
Im
K=100
P=0; R=-2;
Z=0-(-2)=2 闭环系统在 s 右半平面有两个 极点，系统不稳定
-1
+∞
ω=0
Re
闭环传递函数在复平面右半平面有Z个极点
Z PR
R(>0)为Nyquist曲线逆时针包围（-1，j0）点的圈数; R(<0)为Nyquist曲线顺时针包围（-1，j0）点的圈数;
➢只要在这个闭合曲线 内没有F(s)的零点，系 统即为稳定的。
+∞ Im ∞
O Re
-∞
3
5-5 频域稳定判据（奈氏判据）
自动控制原理
➢对于真有理分式，s等于无穷
大的时候，|G(s)H(s)|=0，在
+∞ Im
G(s)H(s)曲线中对应坐标原点。
∞
➢我们只需考察S在虚轴上取值
O
的情况
Re
➢ s j 在复平面上的
自动控制原理
(2)开环传递函数含ν 个积分环节 ν型系统
Ga (S )
K S (TS 1)
Im
-1
0
(a)ν=1,从 0 点逆时针
0 Re
补画半径为无穷大的1/4圆。
0
P=0, N=0，Z=0，
所以，闭环系统稳定。
22
5-5 频域稳定判据（奈氏判据）
自动控制原理
Im
0 -1 0
＝0
曲线G，( j就)是HN( jyq)uist曲线
-∞
4
5-5 频域稳定判据（奈氏判据）

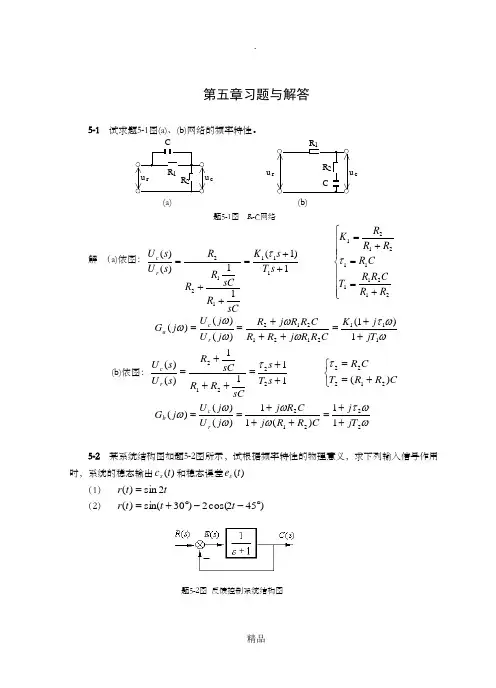
自动控制原理第五章习题及答案

自动控制原理第五章习题及答案

第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。

u r R1u cR2CR2R1u r u c(a) (b)题5-1图R-C网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图：⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++==5-2某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs和稳态误差)(tes（1）tt r2sin)(=（2）)452cos(2)30sin()(︒--︒+=ttt r题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ（2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ )]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应h t e e t tt ()..=-+≥--11808049试求系统频率特性。

自控原理第五章习题参考答案

自控原理第五章习题参考答案

5-1 5()0.251G s s =+5()0.251G j j ωω=+()A ω=()arctan(0.25)ϕωω=-输入 ()5cos(430)5sin(460) =4r t t t ω=-︒=+︒(4)A ==(4)arctan(0.25*4)45ϕ=-=-︒系统的稳态输出为()(4)*5cos[430(4)]3045)17.68cos(475)17.68sin(415)c t A t t t t ϕ=-︒+=-︒-︒=-︒=+︒ sin cos(90)cos(90)cos(270)αααα=︒-=-︒=+︒或者，()(4)*5sin[460(4)]6045) 17.68sin(415)c t A t t t ϕ=+︒+=+︒-︒=+︒所以，对于cos 信号输入下的稳态输出计算规律与sin 信号作用下计算相同。

5-3（2）1()(1)(12)G s s s =++ 1()(1)(12)G j j j ωωω=++()A ω=()arctan arctan 2ϕωωω=--起点：0ω= (0)1;(0)0A ϕ==︒ 位于正实轴上。

终点：ω→∞ ()0;()180A ϕ∞=∞=-︒+∆ 从第三象限趋于原点因此，，Nyquist 曲线与虚轴有交点，并且满足：()arctan arctan 290ϕωωω=--=-︒ arctan arctan 290ωω+=︒所以有，1/(2)ωω= 21/2ω=()0.473A ω=== 因此，与虚轴的交点为（0，-j0.47）()ω（3）1()(1)(12)G s s s s =++ 1()(1)(12)G j j j j ωωωω=++()A ω=()90arctan arctan 2ϕωωω=-︒--起点：0ω= (0);(0)90A ϕ=∞=︒∆－－ 位于负虚轴（左侧）无穷远方向终点：ω→∞ ()0;()270A ϕ∞=∞=-︒+∆ 从第二象限趋于原点因此，，Nyquist 曲线与实轴有交点，并且满足：()90arctan arctan 2180ϕωωω=-︒--=-︒ arctan arctan 290ωω+=︒1/(2)ωω= 21/2ω=2()0.673A ω===与实轴的交点为（-0.67，-j0）)ω（4）21()(1)(12)G s s s s =++ 21()()(1)(12)G j j j j ωωωω=++()A ω=()180arctan arctan 2ϕωωω=-︒--起点：0ω= (0);(0)180A ϕ=∞=︒∆－－ 位于负实轴（上侧）无穷远方向终点：ω→∞ ()0;()360A ϕ∞=∞=-︒+∆ 从第一象限趋于原点因此，，Nyquist 曲线与虚轴有交点，并且满足：()180arctan arctan 2270ϕωωω=-︒--=-︒ arctan arctan 290ωω+=︒1/(2)ωω= 21/2ω=()0.94A ω===与虚轴的交点为（0，j0.94）)ω=5-4（2）10.5ω=，21ω=，1K =，0ν=（3）10.5ω=，21ω=，1K =，1ν=低频段直线（延长线）与0db 线交点的频率为：1/cK νω'=。

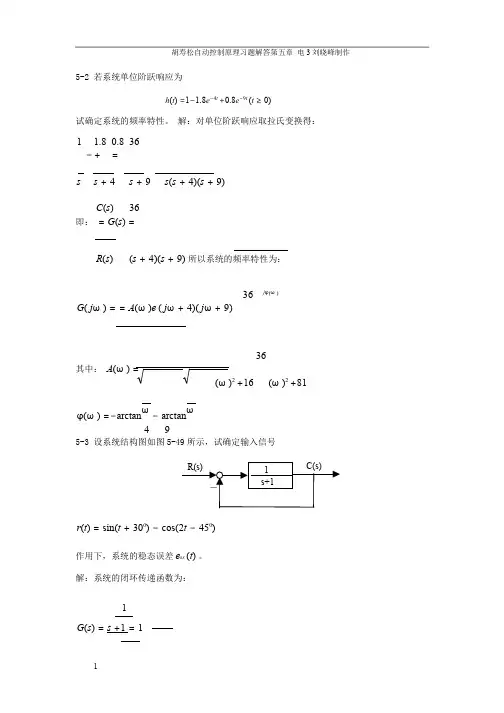
自动控制原理简明教程第二版课后答案第五章习题答案

自动控制原理简明教程第二版课后答案第五章习题答案

5-13 试用奈氏判据分宾判断题 5-5，5-6 系统的闭环稳定性。 解：5-5 （1）τ > T 时系统闭环稳定。 （2）T >τ 5-6 （1）ν =1 时系统闭环稳定。 （2）ν = 2,3,4 时系统闭环不稳定。 5-14 已知下列系统开环传递函数（参数 K,T,Ti > 0;i = 1,2,,6 ） ： 时系统闭环不稳定。
8
胡寿松自动控制原理习题解答第五章 电 3 刘晓峰制作
L（ω ） （dB）
60 40 20
-20 -40 -20
0
0.1 1 2 10
-40 20 -60
100ω
ω 0 − 90

−180
5-11 绘制下列函数的对数幅频渐进特性曲线：
2
（1）G(s) =
(2s +1)(8s +1) 200 （2）G(s) = s 2(s +1)(10s +1)
1
所以：G(s) = 100(0.001s/ω
1
+1)
(s
/ω 1 +1)(s /100 +1)
11
胡寿松自动控制原理习题解答第五章 电 3 刘晓峰制作
（b）G(s) = s 102 (s(s/ω /ω
21
++11) )
（c）
G(s) = (s
2
2ξ ω nKs+2ω + s
n 2
ω
n
2
)(s /10 +1)

0.5 −87.2

1 −92.1
3 −164

5 − 216

7 − 234.5
10 − 246

自动控制原理（黄坚）第五章答案

自动控制原理（黄坚）第五章答案

第五章 频率特性法习题5-1 单位反馈控制系统的开环传递函数110)(+=s s G ，当下列信号作用在系统输入端时，求系统的稳态输出。

(1) )30sin()(︒+=t t r (2) )452cos(2)(︒-=t t r (3) )452cos(2)30sin()(︒--︒+=t t t r 解：本题注意事项：一定要用闭环传递函数求模求角，计算角度一定要看象限 （1）1110)(+=Φs s ，1110)(+=Φωωj j ， ︒-∠=-∠=+=Φ-19.5905.0111122101110)1(1tg j j )8.24sin(905.0)19.530sin(905.0)(︒+=︒-︒+=t t t c ss(2)︒-∠=+=Φ3.10894.011210)2(j j)3.552cos(788.1)(︒-=t t c ss（3）)3.552cos(788.1)8.24sin(905.0︒--︒+=t t c ss5-2 设控制系统的开环传递函数如下，试绘制各系统的开环幅相频率特性曲线和开环对数频率特性曲线。

(1))15)(5(750)(++=s s s s G (2) )1008()1(1000)(2+++=s s s s s G (3) 13110)(++=s s s G解：（1）起点s 10，︒-∞∠90；终点3750s ，︒-∠2700；交点5.0)75(-=j G （2）起点s 10，︒-∞∠90；终点21000s，︒-∠1800；交点)100927()1(1000)(232-++-=s s s s s s G ，)]92()1007[()1(1000)(222ωωωωωω--++=j j j G ，03.13)92(j j G -= （3）起点1；终点，3.33，与坐标轴无交点；曲线在第一象限(1)(2)5-4 最小相位系统对数幅频特性曲线如图所示，试写出他们的传递函数。

解： (a)11.010)(+=s s G (b)105.01.0)(+=s s s G (c))101.0)(1100(100)(++=s s s s G(d))101.0)(11.0)(1(19.251)(+++=s s s s G （书后答案有误）5-5 试由下述幅值和相角计算公式确定最小相位系统的开环传递函数。

自动控制原理第五章课后答案

自动控制原理第五章课后答案

五 频域分析法2-5-1 系统单位阶跃输入下的输出)0(8.08.11)(94≥+-=--t e e t c tt ,求系统的频率特性表达式。

【解】： 98.048.11)]([L )(1+++-==-s s s t c s C 闭环传递函数)9)(4(36198.048.11)()()(++=+++-==s s ss s s s R s C s G )9tg 4(tg 2211811636)9)(4(36)(ωωωωωωω--+-+⨯+=++=j ej j j G2-5-2系统时，系统的稳态输出（1）)30sin()(0+=t t r ； （2）)452cos(2)(0+=t t r ；（3）)452cos(2)30sin()(00--+=t t t r 。

【解】：求系统闭环传递函数5tg 21254)5(4)(54)(1)()()()(14)(ωωωω--+=+=+=+==+=j B K K B K ej j G s s G s G s R s C s G s s G根据频率特性的定义，以及线性系统的迭加性求解如下：（1）︒===30,1,11θωr A︒--====-3.1151tg )1(178.0264)1()(1j j j B e eeA j G θωω[])7.18sin(78.0)1(sin )1()sin()(12︒+=++=+=t t A A t A t c r c s θθθ（2）︒===45,2,21θωr A︒--==+=-8.2152tg 274.02544)(1j j B e ej G ωω)2.232cos(48.1)(︒+=t t c s（3）)8.662cos(48.1)7.18sin(78.0)(︒--︒+=t t t c s2-5-3 试求图2-5-3所示网络的频率特性，并绘制其幅相频率特性曲线。

【解】：（1）网络的频率特性1)(111)(212212+++=+++=ωωωωωC R R j C jR C j R R C j R j G（2）绘制频率特性曲线)tg (tg 22212121111)(1)(11)(ωωωωωωωT T j eT T jT jT j G ---++=++= 其中1221221,)(,T T C R R T C R T >+==。

自动控制原理及其应用课后习题第五章答案

自动控制原理及其应用课后习题第五章答案
40 20 0 -20 -20dB/dec 10 1 2ωc -40dB/dec -60dB/dec 40 -40dB/dec
ω
20 0 -20
10 ωc
1
2 -20dB/dec
ω
-60dB/dec
10 ≈1 ω2 0.5 c
ω c=4.5
5 ≈1 ω c=7.9 ω 0.01 c3
第五章习题课 (5-17)
-20
低频段曲线： 低频段曲线： 20lgK=20dB φ (ω ) 0 ω1=5 ω2=15 -90 相频特性曲线： 相频特性曲线： -180 -270 φ ( )= -90o ω ω=0 φ ( )= -270o ω ω=∞
-60dB/dec
ω
第五章习题课 (5-2)
10(s+0.2) 1.33(5s+1) (5) G(s)= s2(s+0.1)(s+15)=s2(10s+1)(0.67s+1) 解： 低频段曲线： 低频段曲线： 20lgK=2.5dB
第五章习题课 (5-7)
5-7 已知奈氏曲线，p为不稳定极点个数， 已知奈氏曲线， 为不稳定极点个数 为不稳定极点个数， υ为积分环节个数，试判别系统稳定性。 为积分环节个数，试判别系统稳定性。 Im υ=2 (b) p=0 (a) p=0 Im υ=0
ω=0 Re -1 0 ω=0+ -1 0 ω=0 Re
第五章习题课 (5-1)
5-1(1) 已知单位负反馈系统开环传递函数， 已知单位负反馈系统开环传递函数， 当输入信号r(t)=sin(t+30o)，试求系统的稳态 当输入信号 ， 输出。 输出。 10 G(s)=(s+1) 10 解： φ(s)= (s+11) 10 = 10 = 10 ω A( )= 2 2 112+1√ 122 =0.905 √ 11 +( ) √ ω φ ( )=-tg-1ω =-tg-1 1 =-5.2o ω 11 11 cs(t)=0.9sin(t+24.8o)

自动控制原理作业及答案.

自动控制原理作业及答案.


j (1
15 j 2)(1
j
6)
A constant gain K=15 20lg K 23.5dB A pole at origin slope: -20dB/dec A pole at ω=2 slope: -20dB/dec A pole at ω=6 slope: -20dB/dec
③ A pole at ω= 2
slope: -20dB/dec
④ A zero at ω= 3
slope: 20dB/dec
⑤ A pole at ω= 4
slope: -20dB/dec
⑥ A zero at ω= 5
《自动控制原理》
slope: 20dB/dec
第五章 控制系统的频域分析
(1) Logarithm magnitude frequency characteristic Asymptote
101
/ rad / sec
第五章 控制系统的频域分析
2. A control system has an open-loop transfer function G(s)H (s) (s 3)(s 5) s(s 2)(s 4)
Sketch Bode diagram of the system.
6)

15
《自动控制原理》
K1 15 Select K1 15
第五章 控制系统的频域分析
(2) Draw the Bode plot of K1GH0( j) , and evaluate c0 , pm0 and GM0 .
K1GH0( j)
K1G0( j)
180 j( j 2)( j 6)

《自动控制原理》第5章习题答案

《自动控制原理》第5章习题答案

jω
期望极点
期望极点
− p3
j
600
j0.58
− p2
-1
− p1
0 -j
-3
-2
σ
-2
19.150 -1
40.880 0.33 0
119.640
校核相角条件： 根据在图中主导极点位置的近似值－0.33 ± j 0.58 和开环极点的位置， 作由各开环极点到期望主导极点的向量，
Φ = －119.640 －40.880 －19.150 = －179.670≈－1800
− p2
-10 -5
− p1
0
σ
②计算期望主导极点位置。
超调量σ％ ≤ 20％，调整时间 ts ≤ 0.5s
4
ζω n
= 0.5s ， ζω n = 8
σ%=e
−
ζπ
1−ζ 2
= 0.2 ， ζ = 0.45 ， θ = 63.2 0
故，期望主导极点位置， s1, 2 = −8 ± j15.8
期望极点
Gc ( s ) =
4，控制系统的结构如图 T5.3 所示，Gc(s)为校正装置传递函数，用根轨迹法设计校正装置，
使校正后的系统满足如下要求，速度误差系数 Kv ≥ 20，闭环主导极点 ω n = 4 ，阻尼系数 保持不变。
R(s)
+ -
Gc(s)
4 s ( s + 2)
Y(s)
图 T5.3
解：①校核原系统。
14
+20
0dB
1
Φ (ω ) 度
900 00
5
ω rad/s
ω rad/s
2，控制系统的结构如图 T5.1 所示，试选择控制器 Gc(s)， 使系统对阶跃响应输入的超调量

《自动控制原理》答案 李红星 第五章

《自动控制原理》答案 李红星 第五章
由上式可得
0<K <
3 2
b 、 K = 10 时，对于开环幅相曲线与实轴的交点有
Kω (T ω 2 − 1) 10ω (T ω 2 − 1) = =0 (T + 1)2 ω 4 + ω 2 (T ω 2 − 1)2 (T + 1)2 ω 4 + ω 2 (T ω 2 − 1)2
由上式可得 ω =
1 ，则交点的实轴坐标为 T
− K (τ j∞ + 1) = 0, ϕ (∞) = −180o ∞ 2 (Tj∞ + 1)
又由于 G ( jω ) H ( jω ) =
− K (τ jω + 1) − K (τ T ω 2 + 1) + jK ω (T − τ ) = ，所以有 ω 2 (Tjω + 1) ω 2 (T 2ω 2 + 1)
要求画出以下 4 种情况下的奈奎斯特曲线，并判断闭环系统的稳定性： a． T2 = 0 ；
141
b． 0 < T2 < T1 ； c． 0 < T2 = T1 ； d． 0 < T1 < T2 。 解： a． 当 T2 = 0 时， Q ( s ) =
K ， s (T1 s + 1)
2
其开环幅相曲线如题 5-5 解图 a 所示， P = 0 ，N=2 则 Z=P+N=2，故在 s 平面右半平面有 2 个闭环极点，闭环系统不稳定； b．当 0 < T2 < T1 时， Q( jω ) =
a 、 T = 2 时，对于开环幅相曲线与实轴的交点有
K ω (T ω 2 − 1) K ω (2ω 2 − 1) = =0 (T + 1) 2 ω 4 + ω 2 (T ω 2 − 1)2 9ω 4 + ω 2 (2ω 2 − 1) 2

《自动控制原理》课后习题答案(5章)

《自动控制原理》课后习题答案(5章)

《自动控制原理》课后习题答案（5章）5.1 系统的结构图如图5-68所示。

试依据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出ss c 和稳态误差ss e 。

⑴()t t r 2sin =⑵()()()︒︒--+=452cos 230sin t t t r图5-1解 系统的传递函数：()()()21+==Φs s R s C s ()()()21++==Φs s s R s E s e 幅频特性及相频特性：()()2,2122ωωωωarctgj j -=Φ+=Φ()()2,21222ωωωωωωarctgarctg j e e -=Φ++=Φ（1）()2,2sin ==ωt t r 稳态输出：()()︒︒-=-+=452sin 221452sin 441t t c ss()︒-≈452sin 354.0t稳态误差：⎪⎭⎫ ⎝⎛-+++=2222sin 2221222arctg arctg t e ss()()︒︒+≈+=43.182sin 791.043.182sin 225t t（2）()()()()()︒︒︒︒+-+=--+=452sin 230sin 452cos 230sin t t t t t r⎪⎪⎭⎫ ⎝⎛+∠+++•-⎪⎪⎭⎫ ⎝⎛+∠+++=︒︒221452sin 221212130sin 211222j t j t c ss ()t t 2sin 225.3sin 55-+=︒ ()t t 2sin 708.05.3sin 447.0-+≈︒⎪⎭⎫ ⎝⎛-++++•-⎪⎭⎫ ⎝⎛-++++=︒︒222452sin 2221221130sin 12112222222arctg arctg t arctg arctg t e ss ()()︒︒︒︒︒︒-++•--++=4543.63452sin 410257.264530sin 510t t ()()︒︒+-+≈43.632sin 582.143.48sin 632.0t t ()()︒︒--+=57.1162sin 582.143.48sin 632.0t t5.2 若系统的单位阶跃响应：()t t e e t h 948.08.11--+-=()0≥t 试求系统的频率特性。

自动控制原理课后习题答案第五章

自动控制原理课后习题答案第五章

⾃动控制原理课后习题答案第五章第五章5-2 若系统单位阶跃响应为49()1 1.80.8t t h t e e --=-+试确定系统的频率特性。

分析先求出系统传递函数，⽤j ω替换s 即可得到频率特性。

解：从()h t 中可求得：(0)0,(0)0h h '==在零初始条件下，系统输出的拉普拉斯变换()H s 与系统输出的拉普拉斯变换()R s 之间的关系为()()()H s s R s =Φ?即()()()H s s R s Φ= 其中()s Φ为系统的传递函数，⼜1 1.80.836()[()]49(4)(9)H s L h t s s s s s s ==-+=++++1()[()]R s L r t s == 则()36()()(4)(9)H s s R s s s Φ==++ 令s j ω=，则系统的频率特性为()36()()(4)(9)H j j R j j j ωωωωωΦ==++5-7 已知系统开环传递函数为)1s T (s )1s T (K )s (G 12++-=;（Ｋ、Ｔ1、Ｔ2＞０）当取ω＝１时， o 180)j (G -=ω∠,|Ｇ(ｊω)|＝０.５。

当输⼊为单位速度信号时，系统的稳态误差为0.1，试写出系统开环频率特性表达式G(ｊω)。

分析：根据系统幅频和相频特性的表达式，代⼊已知条件，即可确定相应参数。

解：由题意知：()G j ω= 021()90arctan arctan G j T T ωωω∠=---因为该系统为Ⅰ型系统，且输⼊为单位速度信号时，系统的稳态误差为0.1，即 01()lim ()0.1ss s e E s K →∞===所以：10K = 当1ω=时，(1)0.5G j ==0021(1)90arctan arctan 180G j T T ∠=---=-由上两式可求得1220,0.05T T ==，因此10(0.051)()(201)j G j j j ωωωω-+=+5-14 已知下列系统开环传递函数(参数K 、T 、T2，…，６) (1) )1s T )(1s T )(1s T (K )s (G 321+++=(2))1s T )(1s T (s K )s (G 21++=(3))1Ts (s K )s (G 2+=(4))1s T (s )1s T (K )s (G 221++=(5)3s K)s (G = (6)321s )1s T )(1s T (K )s (G ++=(7))1s T )(1s T )(1s T )(1s T (s )1s T )(1s T (K )s (G 432165++++++= (8)1Ts K)s (G -=(9)1Ts K )s (G +--= (10))1Ts (s K )s (G -= 其系统开环幅相曲线分别如图5-6(1)～(10)所⽰，试根据奈⽒判据判定各系统的闭环稳定性，若系统闭环不稳定，确定其s 右半平⾯的闭环极点数。

《自动控制理论》参考答案第五章

《自动控制理论》参考答案第五章

第五章一、单项选择题1-5：D 、B 、D 、A 、B 6-10：B 、D 、C 、A 、C 11-13：D 、A 、B二、分析计算题5-1解 （a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sCR sC R R R s U s U r c ττ ωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sCR s U s U r c )(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-= 系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω)452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ )4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ （2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m s ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m s ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-4解 ()()()12G j K j K e j ==-+ωωπω=→∞00,()G j ω→∞∞=,()G j 0ϕωπ()=-2幅频特性如图解5-4(a)。

中文版教材习题五答案

中文版教材习题五答案


z
*

30 199
30
（2）分离点为： d 0.4 ，分离角为： (2k 1)
l
2
起始角： p4 268 ， p5 268
与虚轴的交点：
K1*

0 0
K2,3*

1.034 73.04
K4*,5165.553104
K(3s 1)
s(2s 1) K(3s 1)
闭环特征方程： 2s 2 (1 3K)s K 0
闭环特征根： s1,2 (1 3K)
(1 3K)2 8K (1 3K) 9K 2 2K 1

4
4
当
K＝0
时，特征根
s1

0, s2


1 2
(1 3K ) (3K 1)2 8
(1)
G(s)

K s(s 1)2
(2)
G(s)

K(s s(s2 4s
4) 29)
(3) G(s)
K
s(s 2 4s 8)
试概略画出闭环系统根轨迹图。 5-4 参考答案：
(a) G(s)H (s) K s(s 1)2
(4) G(s) K (s 5)(s 4) s(s 1)(s 3)
-4 -3
Im
-1
0
Re 5
44
“自动控制原理”第五章习题参考答案
5-5
已知开环传递函数为 G(s)H (s)
K s(s 4)(s2 4s 20)
，请概略画出闭环系统根轨。
5-5 参考答案：
与虚轴交点：

K

自动控制原理(第2版)(余成波)_第5章习题解答 -

自动控制原理(第2版)(余成波)_第5章习题解答 -

108第5章频率特性法教材习题同步解析5.1 一放大器的传递函数为：G (s )=1+Ts K测得其频率响应，当ω=1rad/s 时，稳态输出与输入信号的幅值比为12/2，稳态输出与输入信号的相位差为－π/4。

求放大系数K 及时间常数T 。

解：系统稳态输出与输入信号的幅值比为A ==222172K T ω=+ 稳态输出与输入信号的相位差arctan 45T ϕω=-=-︒，即1T ω=当ω=1rad/s 时，联立以上方程得T =1，K =12放大器的传递函数为：G (s )=121s +5.2 已知单位负反馈系统的开环传递函数为5()1K G s s =+ 根据频率特性的物理意义，求闭环输入信号分别为以下信号时闭环系统的稳态输出。

（1）r （t ）=sin （t +30°）； （2）r （t ）=2cos （2t －45°）；（3）r （t ）= sin （t +15°）－2cos （2t －45°）； 解：该系统的闭环传递函数为65)(+=Φs s 闭环系统的幅频特性为109365)(2+=ωωA闭环系统的相频特性为6arctan )(ωωϕ-=（1）输入信号的频率为1ω=，因此有37375)(=ωA ，()9.46ϕω︒=- 系统的稳态输出()20.54)37ss c t t ︒=+ （2）输入信号的频率为2ω=，因此有()A ω=，()18.43ϕω︒=- 系统的稳态输出()cos(263.43)2ss c t t ︒=- （3）由题（1）和题（2）有对于输入分量1：sin （t +15°），系统的稳态输出如下1() 5.54)37ss c t t ︒=+ 对于输入分量2：－2cos （2t －45°），系统的稳态输出为2()63.43)ss c t t ︒=- 根据线性系统的叠加定理，系统总的稳态输出为)4363.632cos(210)537.5sin(37375)(︒︒--+=t t t c ss5.3 绘出下列各传递函数对应的幅相频率特性与对数频率特性。

《自动控制原理》 第五章习题解答

《自动控制原理》 第五章习题解答
胡寿松自动控制原理习题解答第五章
5-2 若系统单位阶跃响应为
h(t) = 1−1.8e −4t + 0.8e −9t
试确定系统的频率特性。 解：对单位阶跃响应取拉氏变换得：
1 − 1.8 + 0.8 =
36
s s + 4 s + 9 s(s + 4)(s + 9)
(t ≥ 0)
即： C(s) = G(s) =
K,T1,T2 > 0
当取ω = 1时， ∠G( jω ) = −1800 ， G( jω ) = 0.5 。当输入为单位速度信号时，系统的稳
态误差为 0.1，试写出系统开环频率特性表达式。
解： KV
= lim sG(s) = s→0
K
= 10
当ω = 1时 G( jω ) = K (T2ω )2 + 1 = 10 (T2 )2 + 1 = 0.5
T2
=
1 20
T1 = 20
T1
=
1 T2
代入到
G(
j)
=
10
(T2 )2 + 1 (T1 )2 + 1
=
0.5 中得到：
所以系统的开环传递函数为： G(s) = 10(−s / 20 + 1) s(20s + 1)
系统开环频率特性表达式为： G( jω ) = 10(− jω / 20 + 1) jω(20 jω + 1)
ω
2 n
=1
(ω
2 n
− 1)
+
(2ζω n )2
∠GB
(
jω
)
=
−
arctan

自动控制原理参考答案-第5章

自动控制原理参考答案-第5章

第五章题5-1：试绘制下列开环传递函数的幅相频率特性曲线。

(1) 10G(s)H(s)(s 1)(0.2s 1)=++ (2) 25(s 1)G(s)H(s)(s 3)(s 2s 2)+=+++(3) 100G(s)H(s)(s 1)(s 3)(s 4)=+++ 题5-6：试绘制题5-1各开环传递函数的对数幅频特性渐近线和半对数相频特性曲线。

(1) 2221010122()()(1)(0.21)(1)(10.04)j G j H j j j ωωωωωωωω--==++++实频特性：)04.01)(1(210)(222ωωωω++-=P虚频特性：)04.01)(1(12)(22ωωωω++-=Q 相频特性：()arctan arctan 0.2ϕωωω=-- Nyqist 曲线：起点：0ω=(0)10P ⇒=，(0)0Q =，(0)0ϕ=终点：ω=∞()0P ⇒∞=，()0Q ∞=，()180ϕ∞=- 与虚轴交点：()0P ω= 2.236ω⇒=() 3.73Q ω⇒=- Nyqist 曲线如下：转折频率1：111T ω==；转折频率2：215T ω==对数幅频特性：()20lg ()20lg10L A ωω==-半对数相频特性：()arctan arctan 0.2ϕωωω=-- Bode 图如下：(2) 25(1)()()(3)(22)j G j H j j j ωωωωωω+=+-+ 222222225(3)(2)202(12)(9)[(2)4]j ωωωωωωωω+-+-+=+-+ 实频特性：]4)2)[(9(20)2)(3(5)(2222222ωωωωωωω+-++-+=P 虚频特性：]4)2)[(9()21(10)(22222ωωωωωω+-++-=Q相频特性：2()arctan arctan arctan 310.5ωωϕωωω=--- Nyqist 曲线：起点：0ω=5(0)6P ⇒=，(0)0Q =，(0)0ϕ=终点：ω=∞()0P ⇒∞=，()0Q ∞=，()180ϕ∞=-与虚轴交点：()0P ω= 2.09ω⇒=()0.66Q ω⇒=- Nyqist 曲线如下：225(1)0.83(1)()()(3)(22)(0.331)[(0.7)1]j j G j H j j j j j j ωωωωωωωωωω++==+-++++ 转折频率1：11 1.414T ω==；转折频率2：213T ω==对数幅频特性：5()20lg ()20lg 6L A ωω==+半对数相频特性：2()arctan arctanarctan310.5ωωϕωωω=---Bode 图如下：(3) 23222100100[128(19)]()()(1)(3)(4)(1)(3)(4)j G j H j j j j ωωωωωωωωωωω-+-==++++++实频特性：)4)(3)(1()812(100)(2222ωωωωω+++-=P虚频特性：)4)(3)(1()19(100)(2223ωωωωωω+++-=Q 相频特性：()arctan arctan 0.33arctan 0.25ϕωωωω=--- Nyqist 曲线：起点：0ω=(0)8.33P ⇒=，(0)0Q =，(0)0ϕ= 终点：ω=∞()0P ⇒∞=，()0Q ∞=，()270ϕ∞=- 与虚轴交点：()0P ω= 1.22ω⇒=() 4.77Q ω⇒=- 与实轴交点：()0Q ω= 4.36ω⇒=()0.71P ω⇒=- Nyqist 曲线如下：8.33()()(1)(0.331)(0.251)G j H j j j j ωωωωω=+++转折频率1：111T ω==；转折频率2：213T ω==；转折频率3：314T ω==对数幅频特性：()20lg ()18.4L A ωω==-半对数相频特性：()arctan arctan 0.33arctan 0.25ϕωωωω=--- Bode 图如下：题5-2：已知某一控制系统的单位阶跃响应为4t 9t c(t)1 1.8e 0.8e --=-+试求该系统的开环频率特性。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

5.1（1）)(20)(20)(20)(12)(t r t r t c t c t c+=++ （2）21)10)(2()1(20)(ss s s s C ∙+++==s s s s 4.0110275.02125.02+++-++- 所以 c(t)=4.0275.0125.0102++----t e e t t c(0)=0;c(∞)=∞;（3）单位斜坡响应，则r(t)=t所以t t c t c t c2020)(20)(12)(+=++ ，解微分方程加初始条件 解的： 4.04.02)(102++-+=--t e e t c t t c(0)=2, c(∞)=∞; 5.2(1)t t e e t x 35.06.06.3)(---= (2)t e t x 2)(-= (3)tw n n n tw n n n nn n n e w bw a ew bw a t x )1(22)1(222212)1(12)1()(----+----+-+-+----=ξξωξξωξξξωξξξω(4)t a A t a Aa e a a b t x atωωωωωωωcos sin )()(222222+-++++=-5.3(1)y(kT)=)4(1619)3(45)2(T t T t T t -+-+-δδδ+……(2) 由y(-2T)=y(-T)=0;可求得y(0)=0,y(T)=1;则差分方程可改写为y[kT]-y[(k-1)T]+0.5y[(k-2) T]=0;,k=2,3,4….则有0))0()()((5.0))()(()(121=++++----y T y z z Y z T y z Y z z Y2115.015.01)(---+--=zz z z Y =.....125.025.025.05.015431----++++z z z 则y *(t)=0+)5(25.0)4(25.0)3(5.0)2()(T t T t T t T t T t -+-+-+-+-δδδδδ+… (3)y(kT)=k k k k k TT k T T )1(4)1(4)1(4)1(4++---- 5.4开环传递函数G(s)=11)1(+∙--s s e Ts G （z ）=)1)(1(11------e z z z z z =111----ez e 因为系统为单位反馈，所以闭环采样系统传递函数为：W （z ）=)(1)()()(z GH z G z R z C +==1111111------+--e z e e z e =)21(111-----e z e 当系统为单位阶跃输入时，C （z ）=W(z)R(z)= )21(111-----e z e 1-z z =)21(5.015.01-------e z z z z 所以c(kT)=-0.5(1)k +0.5()ke 121-- ,k=0,1,2… 5.5由电路图可得：Ri+y(t)=x(t) ; i=Cdt t dy )( 由上试得出系统传递函数G(s)=11.0+sG(z)=Tez z--1.0 Y(z)=G(z)X(z)= T e z z --1.0T e z z --100=2)(1010T T T e z ze e z z ----+- 所以y(kT)=10(1.0-e )k +10k(1.0-e )k ,k=0,1,2…5.6 解：对于惯性环节，当4t T =时，输出到达稳态输出的98%，所以由题意得4T=60s ，所以环节参数T=15。

5.7已知系统闭环传递函数，求瞬态性能指标，并画出单位阶跃响应曲线（1）29()39W s s s =++解：由2391232n n n ωωξξω=⎧⎧=⎪⎪⇒⎨⎨==⎪⎩⎪⎩3πϕ==，2d ωω==可得：0.806r dt s πϕω-== 1.209p dt s πω==%100%16.3%e σ=⨯=42.67(2)32(5)s ns nt s t s ξωξω==∆===∆=21.1(2)ln %1.50.83(5)ln %N N σσ-==∆=-==∆=（2）210()10100W s s s =++解：221010110()1010010(0.110)10(0.11)10W s s s s s s s ===⋅++++++所以10,0.1K T ==1012n ωξ⎧==⎪⎪⇒⎨⎪==⎪⎩30.2420.363%100%16.3%40.8(2)30.6(5)21.1(2)ln %1.50.83(5)ln %d r d p ds n s nt st se t s t s N N πϕωωπϕωπωσξωξωσσ====-=====⨯===∆===∆=-==∆=-==∆=5.8解：（1）251()1(25)25(1)125G s s s s s ==++++ 11,25K T ==， 2.51,ξ==>过阻尼，5n ω==11.5d ωω= （2） 2.5>21(s),1,441s C T t T s ξ=∴≈===+ 5.9解：由图得%100%33.3%eσ=⨯=，得0.33ξ=由0.1p d t s πω===，得33.3n ω=1110, 2.257,50,0.045KKT K T T ∴==== 11,K K T a a==，所以1222.2,1111,3a K K ===5.10 解： ()()1121258.02525K s K K s K s C t +++=2111 1.4425360.312250.812n t n t K K K K K ωξω=⎧==⎧⎪∴⇒⎨⎨==+=⎪⎩⎩1=ξ为临界阻尼系统， 8.075.4==ns t ω5.11解：（1）加入速度反馈前12212()()K K C s R s Ts s K K =++ 当1240,0.5,0.2,2K K T τ====时，()()C s R s =21005100s s ++100.25n ωξ====41.6(2)31.2(5)s ns nt s t s ξωξω==∆===∆=%100%44.4%e σ=⨯= 加入速度反馈后122212()()(1)K K C s R s Ts K s K K τ=+++ 当1240,0.5,0.2,2K K T τ====时，()()C s R s =210010100s s ++ 2101000.5210n n n ωωξξω⎧==⎧⎪∴⇒⎨⎨==⎪⎩⎩40.8(2)30.6(5)s ns nt s t s ξωξω==∆===∆=%100%16.3%e σ=⨯=（2）为使加入速度反馈后1ξ=1=，即0.511,64ττ+==临界阻尼时，1210n s s ω==-=- 其调节时间24.750.475s t s s ==- 5.12解：系统为Ι型系统，静态误差系数为：,,02np v a K K K ωξ=∞== 设其开环传递函数为20()(2)n n G s s s s ωω=+其误差传递函数为：222012()1()2n E n ns sW s G s s s ξωξωω+==+++ =222214nn s s ξξωω-++……所以20122,,,214n n K K K ωωξξ=∞==-……5.13解：该系统为一型系统,100,0p v a K K K =∞==。

输入信号为二阶，一型系统不能跟踪二阶信号，所以系统稳态误差为无穷大。

5.14已知单位反馈系统的闭环传递函数和在单位阶跃作用下的误差，求阻尼比，无阻尼自然振荡频率和在单位斜坡输入作用下的稳态误差。

解：单位阶跃信号1()R s s=误差响应21()24E s s s =-++ 误差传递函数2()(6)()()68E E s s s W s R s s s +==++设该系统开环传递函数为0()(1)K G s s Ts =+，其中1,22n nK T ωξξω==其误差函数应为22222126()1()268n E n n s s s s W s G s s s s s ξωξωω++===+++++ 所以28,26n n ωξω==所以4n ξω== 004lim ()3v s K s G s →=⋅=134ss v e K == 5.15解：（1）1122()12s s G s s s-+==+ （2）①2110(),()915W s R s s s s==++ 210()()()(915)C s W s R s s s s ==++02()l i m ()3s c s C s →∞=⋅=②系统的开环传递函数为：01()(2)(7)G s s s =++21155(),5,1591510n W s s s ωξ=⋅==++ 为过阻尼系统，因此不会出现峰值和超调。

01()(2)(7)G s s s =++ ， 为0型系统。

()()()()()328721110lim 110limlim lim 00000=+++=+⋅===→→→→s s s G s s s sE t e e s s s t ss。