实振型与复振型分解反应谱法

复振型分解反应谱法复振型分解反应谱法（Multiple Degree of Freedom Modal Analysis Method）是一种结构动力学分析方法，适用于多自由度体系的振动问题。

它通过将结构系统划分为多个振型，从而简化振动问题的求解过程，提供了一种有效的分析工具。

对于一个多自由度体系，其振动方程可以表示为：[M]{u}''+[C]{u}'+[K]{u}={F}其中[M]、[C]和[K]分别是质量矩阵、阻尼矩阵和刚度矩阵，{u}是位移向量，{F}是外力向量。

复振型分解反应谱法的基本思想是通过将位移向量{u}分解为一系列振型分量的叠加，使得振动方程能够化简为多个单自由度振动方程。

为了实现这个目标，首先需要进行模态分析，确定结构的固有振型和固有频率。

模态分析的过程中，需要求解下面的特征值问题：[K]{\phi}=-\lambda[M]{\phi}其中[K]是结构的刚度矩阵，[M]是质量矩阵，{\phi}是由模态向量组成的矩阵，{\lambda}是由模态频率的平方组成的对角矩阵。

通过解特征值问题，可以得到特征频率和特征向量。

根据特征频率，可以计算结构的固有周期，根据特征向量，可以得到结构的模态形式。

接下来，将位移向量{u}按照模态形式进行分解：{u}=\sum_{i=1}^{N}q_i{\phi}_i其中，{q}是由模态振幅组成的位移向量，{q_i}是第i个模态的振幅。

将位移向量{u}的分解形式代入振动方程，可以得到每个模态的单自由度振动方程：m_i{q_i}''+c_i{q_i}'+k_i{q_i}=f_i其中，m_i、c_i和k_i是第i个模态的质量、阻尼和刚度，f_i 是每个模态对应的外力分量。

对于每个单自由度振动方程，可以采用反应谱法进行求解。

反应谱是结构对地震激励的响应的频率特性分析结果，表示结构的响应在不同频率下的幅值。

通过分析反应谱，可以评估结构对地震的响应程度。

复振型分解反应谱法
复振型分解反应谱法（Complex Modulus Decomposition Method，CMDM）是一种用于分析材料动态响应的方法，它可以对材料在不同频率下的动态响应进行分解，从而得到材料的动态特性。

该方法基于复振型分解原理，将材料的动态响应分解为多个模态的贡献，每个模态代表了不同频率范围内的动态响应。

这些模态可以通过实测或者计算得到，并且可以用于分析材料的动态响应特性。

复振型分解反应谱法的主要优点是可以对材料的动态响应响应进行全面的分析，包括动态响应的频率响应、相位响应、振幅响应等，可以为材料设计和优化提供重要的参考。

此外，该方法还可以用于分析材料的疲劳寿命、耐久性等方面的问题。

然而，复振型分解反应谱法也存在一些局限性，例如需要准确测量材料的动态响应，需要对材料的结构和材料特性进行深入的研究，以及需要对材料的动态响应进行长时间的监测等。

复振型分解反应谱法是一种非常有用的材料动态响应分析方法，可以为材料设计和优化提供重要的参考，但需要在实验和理论方面进行深入的研究和探索。

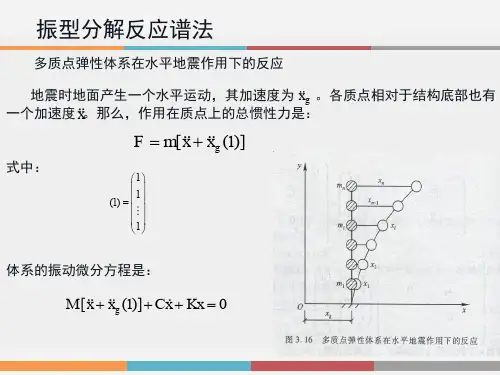
振型分解反应谱法振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。

该法是利用单自由度体系的加速度设计反应谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原则对各阶振型的地震作用效应进行组合，从而得到多自由度体系的地震作用效应。

振型分解反应谱法一般可考虑为计算两种类型的地震作用：不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。

适用条件（1）高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法计算。

（此为底部剪力法的适用范围）（2）除上述结构以外的建筑结构，宜采用“振型分解反应谱法”。

（3）特别不规则的建筑、甲类建筑和规范规定的高层建筑，应采用时程分析法进行补充计算。

刚重比刚重比是指结构的侧向刚度和重力荷载设计值之比，是影响重力二阶效应的主要参数刚重比=Di*Hi/GiDi-第i楼层的弹性等效刚度，可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系；周期比的调整将导致结构侧移刚度的变化，从而影响到刚重比。

因此调整周期比时应注意，当某主轴方向的刚重比小于或接近规范限值时，应采用加强刚度的方法；当某主轴方向刚重比大于规范限值较多时，可采用削弱刚度的方法。

同样，对刚重比的调整也可能影响周期比。

特别是当结构的周期比接近规范限值时，应采用加强结构外围刚度的方法规范上限主要用于确定重力荷载在水平作用位移效应引起的二阶效应是否可以忽略不计。

见高规5.4.1和5.4.2及相应的条文说明。

刚重比不满足规范上限要求，说明重力二阶效应的影响较大，应该予以考虑。

规范下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大，避免结构的失稳倒塌。

见高规5.4.4及相应的条文说明。

刚重比不满足规范下限要求，说明结构的刚度相对于重力荷载过小。

但刚重比过分大，则说明结构的经济技术指标较差，宜适当减少墙、柱等竖向构件的截面面积。

振型分解反应谱法求结构的最大位移和底部最大剪力概述说明以及解释1. 引言1.1 概述本文讨论的是振型分解反应谱法在求解结构的最大位移和底部最大剪力方面的应用。

在工程设计和结构分析中，了解结构的抗震性能是至关重要的，因为地震荷载可能会对结构造成巨大影响。

因此，准确估计结构在地震作用下的位移和剪力变化对于设计可靠、安全稳定的建筑物至关重要。

1.2 文章结构本文共分为五个部分进行详细介绍。

首先，在引言部分我们将概述本文的主题和研究目的。

然后，我们将详细讨论振型分解反应谱法的理论基础、求解过程以及其应用范围与限制。

接着，在第三部分中，我们将探讨如何使用等效静力法原理来求解结构的最大位移，并给出相应的求解步骤和计算公式。

第四部分将重点研究底部最大剪力的求解，包括底部剪力分布特点、剪力计算方法及公式导出过程，并通过数值模拟和实验验证结果对比来进行进一步分析。

最后，我们将在结论与展望部分总结主要研究结论，并对存在问题提出改进方向的展望。

1.3 目的本文的主要目的是介绍和解释振型分解反应谱法在求解结构最大位移和底部最大剪力中的应用。

通过阐述相关理论基础、求解过程以及实例分析，旨在为工程师和研究人员提供一种有效的方法来评估建筑物在地震作用下的抗震性能。

此外，本文还将探讨该方法存在的限制，并提出改进方向，以促进该领域未来的研究和应用发展。

2. 振型分解反应谱法2.1 理论基础振型分解反应谱法是结构动力学中常用的一种分析方法，通过将结构的地震作用响应按照不同振型进行分解，进而求解结构在各个振型下的最大位移和底部最大剪力。

该方法基于以下两个理论基础：首先是振型理论。

振型是描述结构在地震激励下的运动状态的数学函数形式。

结构可通过特征向量与自由振荡频率确定其对应的振型形态。

其次是反应谱理论。

反应谱是一种表征动力响应强度与频率关系的曲线。

通过将地震输入转化为加速度-频率坐标系上的曲线，可以获取到某个特定周期（频率）下结构对地震作用响应的峰值。

实振型与复振型分解反应谱法
首先，我们来看实振型分解反应谱法。

实振型分解反应谱法是一种基于结构固有振动模式进行地震响应分析的方法。

在这种方法中，结构的地震响应被分解为各个振动模式的响应之和。

每个振动模式对应结构的一个固有振动频率和振型，通过对结构的所有振动模式进行叠加，可以得到结构在地震作用下的总响应。

这种方法的优点是能够直观地展示结构在不同振动模式下的响应特性，有利于工程师对结构的地震响应进行分析和评估。

而复振型分解反应谱法则是一种将结构地震响应分解为实部和虚部的方法。

在这种方法中，结构的地震响应被分解为实部和虚部的反应谱，实部反映了结构的动态特性，而虚部则反映了结构的耗能特性。

通过对实部和虚部的分析，可以更全面地了解结构在地震作用下的响应情况，有利于工程师进行结构的抗震设计和评估。

从工程实践的角度来看，实振型与复振型分解反应谱法都是有效的工具，可以帮助工程师更好地理解结构在地震作用下的响应情况。

在实际工程中，工程师可以根据具体的结构特点和设计要求选择合适的分解反应谱方法，以便更准确地评估结构的抗震性能并进行合理的设计优化。

总的来说，实振型与复振型分解反应谱法都是结构地震响应分析中重要的方法，它们各自具有独特的优势，可以帮助工程师更全面地理解和分析结构在地震作用下的响应情况，从而为结构的抗震设计和评估提供重要的参考依据。