9工程力学材料力学答案

(a) (b)习题1-1图 【最新整理，下载后即可编辑】1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。

试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。

解：（a ），图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。

（b ），图（d ）：1y F x xF 1y Fα1xF y F（c ）2F2y F2y2x 2x F2y FF（d ）(a) (b)习题1－2图F DR AC BD AxF AyF(a-1)Ay F FB C A AxF 'F C(a-2) C DF DR(a-3)AxFF A C BD AyF (b-1) 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j FϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。

1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。

比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。

1－3 试画出图示各物体的受力图。

习题1－3图F AxFAyF D C BABF或(a-2)FB AF DCA(a-1)BF AxF AAyF C(b-1)WF BD CF FCBBF AACBF(f-1)(e-3)'A(f-2)1O(f-3)c FF AF DF BF AF A习题1－4图1－4 图a所示为三角架结构。

力F1作用在B铰上。

杆AB 不计自重，杆BD杆自重为W。

试画出图b、c、d所示的隔离体的受力图，并加以讨论。

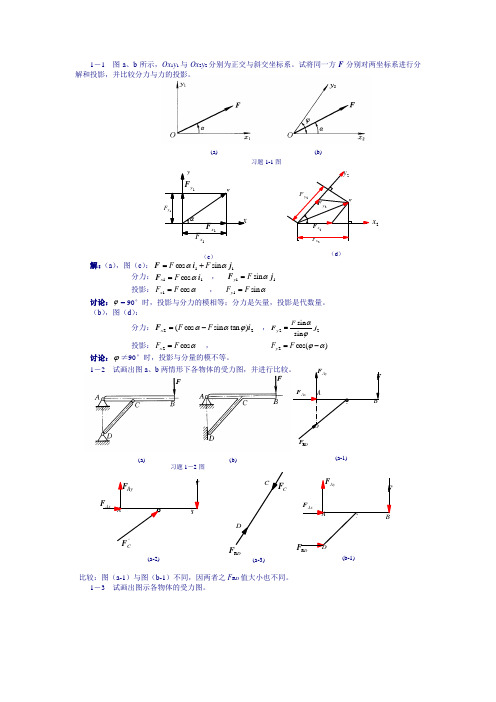
(a) (b) 习题1-1图 (a) (b) 习题1－2图FD R F ACBDAx F AyF(a-1) Ay F F B C A Ax F 'F C(a-2)C D F D R F(a-3)AxF F FA C BD Ay F(b-1) 1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。

试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。

解：（a ），图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。

（b ），图（d ）：分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。

1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。

比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。

1－3 试画出图示各物体的受力图。

1y F x 1F 1y F α1x F y F （c ）x F 2y F 2y 2x 2x F 2y F F （d ）习题1－4图习题1－3图1－4 图a 所示为三角架结构。

力F 1作用在B 铰上。

杆AB 不计自重，杆BD 杆自重为W 。

试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。

F Ax F AyF D C B A B F 或(a-2) F B F A F D C A (a-1) B F AxF AAy F C(b-1)W F B DC Ay F F (c-1) FF C B B F A或(b-2) αD A F A BCBFC F C A A F (e-1) Ax F A Ay FD F D C αF或(d-2)BF F C D B OOx F OyF W 1O F A(f-1)FA F D C AB B F 'F A O Ox F OyF AW (f-2) A 1F A 1O (f-3) c F F A F D F B F AF AAx F C 'CxF 'B F B Ay F 'F CyA (b-3)EF D F E D (a-3) C F F CE 'F E (a-2) 习题1－5图E EF B B F(b-2)Cx F C CyF W T(b-1) B F B C 'CF D 'D F Ax F AyF A1－5 试画出图示结构中各杆的受力图。

1．过受力构件内任一点，取截面的不同方位，各个面上的()。

A.正应力相同，切应力不同B.正应力不同，切应力相同C.正应力相同，切应力相同D．正应力不同，切应力不同2．滚动支座约束的约束反力大小未知、作用线过铰链中心、方向()。

A.与活动方向垂直B.与活动方向平行C.为铅锤方向D.为水平方向3．对称循环时，交变应力的循环特征 r= ()。

A．－1；B．0；C．0.5；D．1。

4.二力杆约束的约束反力大小未知、作用点铰链中心、方向()。

A.未知B.平行于两个铰链的中心连线C.垂直于两个铰链的中心连线D.为水平方向5.下列说法中不正确的是： ()A 力使物体绕矩心逆时针旋转为负B 平面汇交力系的合力对平面内任一点的力矩等于力系中各力对同一点的力矩的代数和C 力偶不能与一个力等效也不能与一个力平衡D 力偶对其作用平面内任一点的矩恒等于力偶矩，而与矩心无关6.圆轴扭转时，表面上任一点处于()应力状态。

A.单向B.二向C.三向D.零7.梁的截面为 T 字型， Z 轴通过横截面的形心，弯矩图如图所示，则有()。

A.最大拉应力和最大压应力位于同一截面 CB.最大拉应力位于截面 C，最大压应力位于截面 DC.最大拉应力位于截面 D，最大压应力位于截面 CD.最大拉应力和最大压应力位于同一截面 D8.下列说法中不正确的是：()。

A 力使物体绕矩心逆时针旋转为负B 平面汇交力系的合力对平面内任一点的力矩等于力系中各力对同一点的力矩的代数和C 力偶不能与一个力等效也不能与一个力平衡D 力偶对其作用平面内任一点的矩恒等于力偶矩，而与矩心无关9.低碳钢材料由于冷作硬化，会使()提高：A 比例极限、屈服极限B 塑性C 强度极限D 脆性10.下列表述中正确的是()。

A.主矢和主矩都与简化中心有关。

B.主矢和主矩都与简化中心无关。

C.主矢与简化中心有关，而主矩与简化中心无关。

D．主矢与简化中心无关，而主矩与简化中心有关。

11.图所示阶梯形杆 AD 受三个集中力 F 作用，设AB、BC、CD 段的横截面面积分别为 2A、3A、A，则三段杆的横截面上()。

静力学部分第一章基本概念受力图工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学汤2-1 解：由解析法，23co s 80R X F X P P Nθ==+=∑12sin 140R Y F YP P Nθ==+=∑故：161.2R F N==1(,)a rc c o s 2944R Y R RF F P F '∠==工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123co s 45co s 453R X F X P P P K N==++=∑13sin 45sin 450R Y F YP P ==-=∑故：3R F K N== 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：X =∑sin 300A C AB F F -=Y=∑co s 300A C F W -=0.577A B F W=（拉力）1.155A C F W=（压力）（b ） 由平衡方程有：X =∑co s 700A C AB F F -=Y=∑sin 700A B F W -=1.064A B F W=（拉力）0.364A CF W=（压力）（c ） 由平衡方程有：X =∑co s 60co s 300A C AB F F -=Y=∑sin 30sin 600A B A C F F W +-=0.5A B F W= (拉力)0.866A C F W=（压力）（d ） 由平衡方程有：X =∑sin 30sin 300A B A C F F -=Y=∑co s 30co s 300A B A C F F W +-=0.577A B F W= (拉力)0.577A C F W= (拉力)工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2-4 解：（a ）受力分析如图所示：由x =∑4c o s 450R A F P ⋅-=15.8R A F K N∴=由0Y =∑s in 450R A R B F F P ⋅+-=7.1R B F K N∴=(b)解：受力分析如图所示：由x =∑c o s 45c o s 450R A R B F F P ⋅--=Y=∑s in 45s in 450R A R B F F P ⋅+-=联立上二式，得：22.410R A R B F K N F K N==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5R A F K N= （压力）5R B F K N=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2A C F G =由x =∑c o s 0A C r F F α-=12c o s G G α∴=由0Y =∑s in 0A C N F F W α+-=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2s in N F W G W α∴=-⋅=-2-7解：受力分析如图所示，取左半部分为研究对象由x =∑co s 45co s 450R A C B P F F --=Y=∑sin 45sin 450C B R A F F '-=联立后，解得：0.707R A F P=0.707R B F P=由二力平衡定理0.707R B C B C B F F F P'===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑co s 60co s 300A C AB F F W ⋅--=Y=∑sin 30sin 600A B A C F F W +-=联立上二式，解得： 7.32A BF K N=-（受压）27.3A CF K N=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑s in c o s 0D B T W αα-=D B T W c tg α∴==（2）取B 点列平衡方程：由Y=∑s in c o s 0B D T T αα'-=230B D T T ctg W ctg K Nαα'∴===2-10解：取B 为研究对象：工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理由Y=∑s in 0B C F P α-=sin B C P F α∴=取C 为研究对象：由x =∑c o s s in s in 0B C D C C E F F F ααα'--=由0Y =∑s in c o s c o s 0B C D C C E F F F ααα--+=联立上二式，且有B C B CF F '= 解得：2c o s 12s in c o s C E P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象：由0Y =∑c o s 0N H C E F F α'-=C E C EF F '= 故有：22c o s 1c o s 2s in c o s 2s in N H P P F ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750A B A D F F -=Y=∑co s 75co s 750A B A D F F P +-=联立后可得： 2c o s 75A D AB P F F ==取D 点平衡，取如图坐标系：x =∑co s 5co s 800AD N D F F '-=c o s 5c o s 80N D A DF F '=⋅由对称性及A D A DF F '=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理c o s 5c o s 5222166.2c o s 80c o s 802c o s 75N N D A D P F F F K N'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑co s co s 300R A D C F F P α+-=Y=∑sin sin 300R A F P α-=联立上二式得：2.92R A F K N=1.33D C F K N=（压力）列C 点平衡x =∑405D C A C F F -⋅=Y=∑305B C A C F F +⋅=联立上二式得：1.67A C F K N=（拉力）1.0B CF K N=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑R D R E F F '=Y =∑R D F Q =联立方程后解得：R D F =2R E F Q'=（2）取ABCE 部分，对C 点列平衡x =∑co s 450R E R A F F -=Y=∑sin 450R B R A F F P --=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理且 R ER EF F '=联立上面各式得：R AF =2R B F Q P=+（3）取BCE 部分。

工程力学材料力学考研试题及答案### 工程力学材料力学考研试题及答案#### 一、选择题1. 下列哪项不是材料力学研究的范畴？（）A. 材料的应力-应变关系B. 材料的疲劳寿命C. 材料的热膨胀系数D. 材料的弹性模量答案： C2. 根据胡克定律，当材料受到正应力时，其应变与应力的关系是（）A. 正比B. 反比C. 无关D. 非线性答案： A3. 材料力学中的“屈服强度”指的是（）A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料的弹性模量D. 材料的硬度答案： A#### 二、简答题1. 简述材料力学中“弹性模量”和“剪切模量”的区别。

答案：弹性模量，也称为杨氏模量，是指材料在受到正应力作用下，其应变与应力之间的比值。

它反映了材料抵抗线性弹性变形的能力。

剪切模量，又称为刚度模量，是指材料在受到剪切应力作用下，其剪切应变与剪切应力之间的比值。

它描述了材料抵抗剪切变形的能力。

2. 解释什么是材料的“疲劳寿命”并简述其影响因素。

答案：疲劳寿命是指材料在重复或循环加载条件下，从开始加载到发生疲劳断裂的时间或循环次数。

影响疲劳寿命的因素包括应力水平、加载频率、材料的微观结构、表面处理和环境条件等。

#### 三、计算题1. 某材料的弹性模量为200 GPa，若该材料的一根长直杆受到100 MPa的正应力，求其应变。

答案：根据胡克定律，应变 \( \epsilon \) 与应力 \( \sigma \) 的关系为 \( \epsilon = \frac{\sigma}{E} \)，其中 \( E \) 是弹性模量。

代入数值得：\[ \epsilon = \frac{100 \times 10^6 \text{ Pa}}{200 \times 10^9 \text{ Pa}} = 5 \times 10^{-4} \]2. 已知某材料的屈服强度为250 MPa，若该材料的一根横截面积为50 mm²的杆件在受到2500 N的拉力作用下，判断是否会发生屈服。

1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDC ’B2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。

工程力学(静力学与材料力学)单祖辉 谢传峰合编课后习题答案1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)DBF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

(d)FC(e)WB(f)F FBC(c)(d)(b)(e)解：(a)(b)(c)(d)(e)ATF BAFCAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa ∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S =15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3= 3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ==== AC AC AC L NL EA EA σε===1.59*104, CB CB CB L NL EA EA σε===6.36*1041-8:解:Nll EAl l ε∆=∆= ∴NEA ε=62.54*10N EA N ε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max 59.5MPa σσ=<1-11：解：（1）当45oα=，[]11.2σσ=>强度不够 （2）当60oα=，[]9.17σσ=< 强度够 1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPa σ=<1-14：解： 1.78, 1.26d cm d cm ==拉杆链环1-15 解：BC F ==70.7 kN70.70.505140F S FS σσ=∴=== 查表得： 45*45*31-16解：(1)[]2401601.5ss n σσ===MPa[][]24P SP dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPa S d σπ===≤⎛⎫ ⎪⎝⎭1-17 解：（1） 2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭78.4AC F MPa S σ== 300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F S F S Nσσ===='61544014.521542390F n F ===≈1-18 解：P=119kN1-19 解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kN P kN σ=====同理所以最大载荷 84kN1-20 解： P=33.3 kN1-21 解：71,,12123A B C P F F P F P ===1-22 解：10MAX MPa σ=-1-23 解：A B X R R R =∴==∑t r l l ∆=∆ t A B l l tα∆= 21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1 一螺栓连接如图所示，已知P=200 kN ， =2 cm ，螺栓材料的许用切应力[τ]=80Mpa ，试求螺栓的直径。

2-1 求下列结构中指定杆内的应力。

已知(a)图中杆的横截面面积A 1=A 2=1150mm 2； 解：（1）分析整体，作示力图∑=0)(i BF M：CB 041088=××−×A F AF N1F N2(c)40kN A F =（2）取部分分析，示力图见（b ）∑=0)(i CF M：02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×（3）分析铰E ，示力图见（c ）∑=0ix F ：0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。

（3）图(c)为变截面拉杆，上段AB 的横截面积为40mm 2，下段BC 的横截面积为30mm 2，杆材料的ρg =78kN/m 3。

解：1.作轴力图，BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ，发生在B 截面。

EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm ，直径缩小了0.022mm ，确定材料的弹性模量E 、泊松比µ。