工程力学材料力学答案-第十一章解析

工程力学第十一章习题解答题目：一物体质量为10kg，在水平地面上以10m/s的初速度开始运动，若物体受到一个恒力F=20N的作用，且与运动方向相反，求物体在力作用下停止前所经过的距离。

解答过程：一、问题分析根据牛顿第二定律，力等于质量乘以加速度，即F=ma。

本题中，物体受到一个恒力F=20N的作用，且与运动方向相反，因此加速度a为负值。

我们需要求解物体在力作用下停止前所经过的距离。

二、解题步骤1. 求加速度a根据牛顿第二定律，F=ma，代入已知数据，得到加速度a：a = F/m = -20N / 10kg = -2m/s²2. 求物体停止前所经过的时间t由于物体初速度v0=10m/s，加速度a=-2m/s²，根据速度-时间关系式v=v0+at，我们可以求解物体停止前的时间t：0 = 10m/s - 2m/s² tt = 10m/s / 2m/s² = 5s3. 求物体在力作用下停止前所经过的距离s根据位移-时间关系式s=v0t + 1/2at²，代入已知数据，求解物体在力作用下停止前所经过的距离s：s = 10m/s 5s + 1/2 (-2m/s²) (5s)²s = 50m - 25ms = 25m三、答案验证根据动能定理，物体在运动过程中，动能的变化等于外力做的功。

物体从初始速度10m/s减速到0，动能变化为：ΔK = 1/2 m (v² - v0²) = 1/2 10kg (0 - 100m²/s²) = -500J外力做的功为：W = F s = 20N 25m = 500J由于动能变化等于外力做的功，所以我们的答案是正确的。

四、总结本题主要考查了牛顿第二定律、速度-时间关系式、位移-时间关系式和动能定理的应用。

通过求解加速度、时间和距离，我们得到了物体在力作用下停止前所经过的距离为25m。

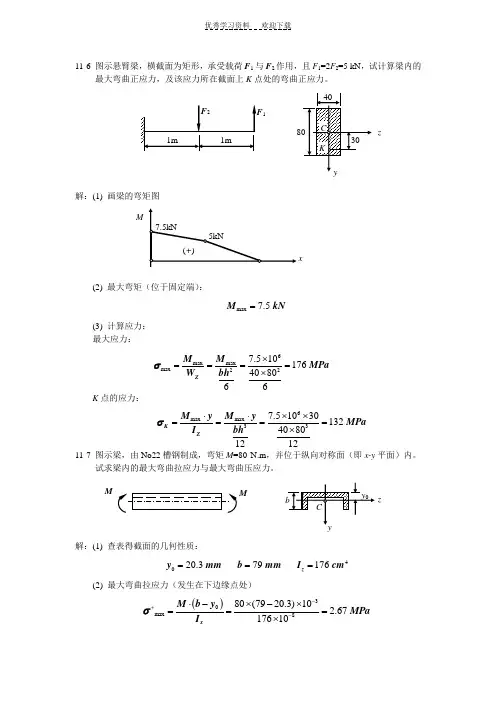
11-6 图示悬臂梁，横截面为矩形，承受载荷F 1与F 2作用，且F 1=2F 2=5 kN ，试计算梁内的最大弯曲正应力，及该应力所在截面上K 点处的弯曲正应力。

解：(1) 画梁的弯矩图(2) 最大弯矩（位于固定端）：max 7.5 M kN =(3) 计算应力： 最大应力：K 点的应力：11-7 图示梁，由No22槽钢制成，弯矩M =80 N.m ，并位于纵向对称面（即x-y 平面）内。

试求梁内的最大弯曲拉应力与最大弯曲压应力。

解：(1) 查表得截面的几何性质：4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力（发生在下边缘点处）()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力（发生在上边缘点处）30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁，由No28工字钢制成，在集度为q 的均布载荷作用下，测得横截面C 底边的纵向正应变ε=3.0×10-4，试计算梁内的最大弯曲正应力，已知钢的弹性模量E =200 Gpa ，a =1 m 。

解：(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为：49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为：2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力：2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁，F =10 kN ，M e =70 kNm ，许用拉应力[σ+]=35 MPa ，许用压应力[σ-]=120 MPa ，试校核梁的强度。

第11章典型习题解析1.用卡氏第二定理求图12.3所示刚架A 截面的位移和B 截面的转角。

略去剪力Q 和轴力N 的影响，E Ⅰ为已知.解：（1）A 截面的位移AB 段弯矩：M(x)=-Px （0≤x ≤l ） ∂M(x) /∂P=-x在A 处虚加一水平力向右的力Q,之后，再令其为0.那么,BC 段弯矩：M(y)=-2P l - Q l +(P+Q)y∂M(y) /∂P=-2l +y ∂M(y) /∂ Q=-l +yA 截面的竖直位移:Y A ==∂∂∑⎰EI P Mdx ML 0 ()()()()⎰⎰+-+-+--L LEIdy y L Py PL EI dx x Px 00222 =EIPL 223A 截面的水平位移: X A =EI Q M M L ∂∂∑⎰0dx=()()EI dy y L Qy Py QL PL L 200+-++--⎰ 积分，令Q=0得 ()()EIPL EI dy y L Py PL XA L 1252230=+-+-=⎰(2)B 截面的转角在B 处虚加一力偶M B,AB 段弯矩：M(x)=-Px （0≤x<l ）BC 段弯矩：M(y)=-2P l -B M +Py （0<y<l ）∂M(x) /∂MB=0 ∂M(y) /∂MB =-1 ∑⎰∂∂=L B B EI dx M M M 0θ =()()⎰-+--L B EI dxPy M PL 0212 EIPL 432= 2.用卡氏第二定理求图示的A 截面的位移和B 截面的转角。

略去剪力Q 和轴力N 的影响，E Ⅰ为已知。

解：（1）A 截面的位移在A 点虚加一向下的力F ，支反力2qL F P Y B ++= （L 为AB 和AD 的长度） P X qL P Y C C -=--=,2AB 段弯矩： M1=0∂ M1 /∂F=0AD 段弯矩：M2(x)=2qL P F qx 2++⋅1（）x-2∂M2(x) /∂F=xCD 段弯矩：M3(y)=PyaⅠⅠ2ⅠC DA 截面的竖直位移:∑⎰∂∂=L A EIdx F M M Y 0=⎰⋅⎥⎦⎤⎢⎣⎡-⋅⎪⎭⎫ ⎝⎛++L EI xdx qx x F qL P 02222 积分，令F=0得34A PL qL Y 6EI 24EI =+求A 截面的水平位移时， 在A 处虚加一水平力向右的力Q, 再令其为0.那么, 支反力B qL Y P Q 2=++ （L 为AB 和AD 的长度）C C qL Y P Q X P Q 2=-+=-+（）+，（） AB 段弯矩： M1=0∂ M1 /∂Q=0AD 段弯矩：M2(x)=(P+Q)x ⋅∂M2(x) /∂Q=xCD 段弯矩：M3(y)=（P+Q ）y∂M3(y) /∂Q=yA 截面的水平位移∑⎰∂∂=L A EI dx Q M M X 0=()⎰⋅+L EIdx x Q P 022=()⎰⋅+L EI ydy y Q P 0积分，令Q=0得 EIPL X A 23= (2) B 截面的转角在B 处虚加一顺时针的力偶M B, 积分，并令其为零。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。

（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。

所有摩擦均不计，各物自重除图中已画出的外均不计。

（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。

梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。

如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。

题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。

转动绞车，物体便能升起。

设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。

电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。

题2-3图以AC 段电线为研究对象，三力汇交2-4 图示为一拔桩装置。

在木桩的点A 上系一绳，将绳的另一端固定在点C ，在绳的点B 系另一绳BE ，将它的另一端固定在点E 。

然后在绳的点D 用力向下拉，并使绳BD 段水平，AB 段铅直；DE 段与水平线、CB 段与铅直线成等角α=0.1rad （弧度）（当α很小时，tanα≈α）。

如向下的拉力F=800N ，求绳AB 作用于桩上的拉力。

题2-4图 作BD 两节点的受力图 联合解得：kN F F F A80100tan 2=≈=α 2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2，，机构在图示位置平衡。

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a 所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN ，吊杆的尺寸如图b 所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS=38.1MPa1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC ACLNL EA EA σε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

单选题
1.在图示结构中，如果将作用于构件AC上矩为M的
力偶搬移到构件BC上，则A、B、C三处约束力的
大小( )。

A．都不变
B．A、B处约束力不变，C处约束力改变；
C．都改变
D．A、B处约束力改变，C处约束力不变
答案:C
知识点：第二章
难度: 4
解析: 力偶的性质
2.下列结论中哪些是正确的（）？
（1）为保证构件能正常工作，应尽量提高构件的强度。

（2）为保证构件能正常工作，应尽量提高构件的刚度。

（3）为保证构件能正常工作，应尽量提高构件的稳定性。

（4）为保证构件能正常工作，应尽量提高构件的强度、刚度和稳定性。

A.（1），（2），（3）
B.（4）
C.全对
D.全错
答案: C
知识点：第五章
难度: 3
解析: 材料力学的定义
3.变截面杆AD受集中力作用，如图所示。

设N AB、N BC、N CD分别表示该杆AB段，BC段和CD 段的轴力，则下列结论中正确的是( )
A.N AB >N BC >N CD
B.N AB =N BC=N CD
C.N AB=N BC >N CD
P
P
D
C
B
A。

第十一章 能量方法第十一章答案11、1 图示桁架各杆的材料相同,截面面积相等。

试求在F 力作用下,桁架的变形能。

12,2N N F F F ==32N F F = 2222222()2222N F F l l F x V dx EA EA EA ε⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=、11、2计算图示各杆的应变能。

(a) 2223244F l F l F l V EA EA EAε=+=、 (b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l e e M M l x x EIl EI ⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭、11、3 传动轴受力情况如图所示。

轴的直径为40mm ,材料为45钢,E = 210GPa ,G = 80GPa 。

试计算轴的应变能。

由扭转引起的应变能:20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能:20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=、11、4 计算图示梁的应变能,并说明就是否满足叠加原理及其原因。

2230()26lFl Fx F lV dx EI EIε-==⎰而22310()22l Fl F lV dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰、不满足叠加原理,因为应变能与内力的关系不就是线性的。

、0、36kN(b)1kN200200 EIMe=FlFlx11、5在外伸梁的自由端作用力偶矩中点C 的挠度w c 。

(见课本下册p40例12-4)11、6 图示刚架的各杆的EI 皆相等,试求截面A 、B 的位移与截面C 的转角。

(a) A 点:在A 点加一个向下的单位力。

M (x 1)=0, M (x 2)=Fx 2, M (x 3)=Fb11()M x x =,22()M x Fx =,3()0M x = 3330()()h M x M x Fabhdx EI EI∆==-⎰、C 点:在C 加一个逆时针的力偶矩为１的单位力偶。

材料力学答案第十一章仅供学习与交流，如有侵权请联系网站删除 谢谢50第十一章 能量方法第十一章答案11.1 图示桁架各杆的材料相同，截面面积相等。

试求在F 力作用下，桁架的变形能。

12,2N N F F F == 32N F F = 222222()2222N F F l l F x V dx EA EA EA ε⎫⎛⎫⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=.11.2计算图示各杆的应变能。

(a)仅供学习与交流，如有侵权请联系网站删除 谢谢512223244F l F l F l V EA EA EAε=+=.(b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l ee M M l x x EIl EI ⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.11.3 传动轴受力情况如图所示。

轴的直径为40mm ，材料为45钢，E = 210GPa ，G = 80GPa 。

试计算轴的应变能。

由扭转引起的应变能：20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能：20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=.11.4 计算图示梁的应变能，并说明是否满足叠加原理及其原因。

2230()26lFl Fx F l V dx EI EIε-==⎰0.08kN· 0.36kN (b) 1kN 2000200EIMe=FlFlx仅供学习与交流，如有侵权请联系网站删除 谢谢52而22310()22lFl F l V dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰.不满足叠加原理，因为应变能与内力的关系不是线性的。

11.5在外伸梁的自由端作用力偶矩M跨度中点C 的挠度w c 。