工程力学--材料力学(北京科大、东北大学版)第4版第六章习题答案
- 格式:doc
- 大小:338.50 KB
- 文档页数:18
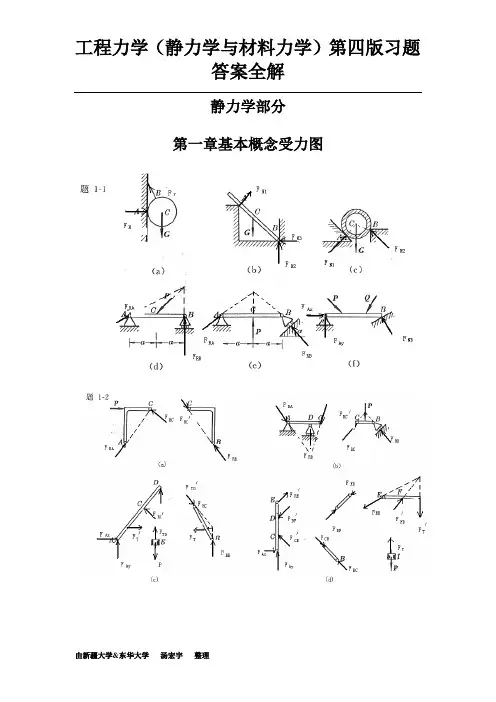
静力学部分第一章基本概念受力图2-1 解:由解析法,23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故:161.2R F N ==1(,)arccos 2944RY R R F F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑ 13sin 45sin 450RY F Y P P ==-=∑ 故:3R F KN == 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑ sin 300AC AB F F -=0Y =∑ cos300AC F W -=0.577AB F W =(拉力) 1.155AC F W =(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑ sin 700AB F W -=1.064AB F W =(拉力)0.364AC F W =(压力)(c ) 由平衡方程有:0X =∑ cos 60cos300AC AB F F -=0Y =∑ sin 30sin 600AB AC F F W +-=0.5AB F W = (拉力)0.866AC F W =(压力)(d ) 由平衡方程有:0X =∑ sin 30sin 300AB AC F F -=0Y =∑ cos30cos300AB AC F F W +-=0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解:(a )受力分析如图所示:由0x =∑cos 450RA F P -=15.8RA F KN ∴=由0Y =∑sin 450RA RB F F P +-=7.1RB F KN ∴=(b)解:受力分析如图所示:由x =∑cos 45cos 450RA RB F F P --=0Y =∑sin 45sin 450RA RB F F P -=联立上二式,得: 22.410RA RB F KNF KN ==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN = (压力) 5RB F KN =(与X 轴正向夹150度) 2-6解:受力如图所示:已知,1R F G = ,2AC F G =由0x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解:受力分析如图所示,取左半部分为研究对象由0x =∑ cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CB RA F F '-= 联立后,解得: 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力) 列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q -=联立方程后解得:RD F =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
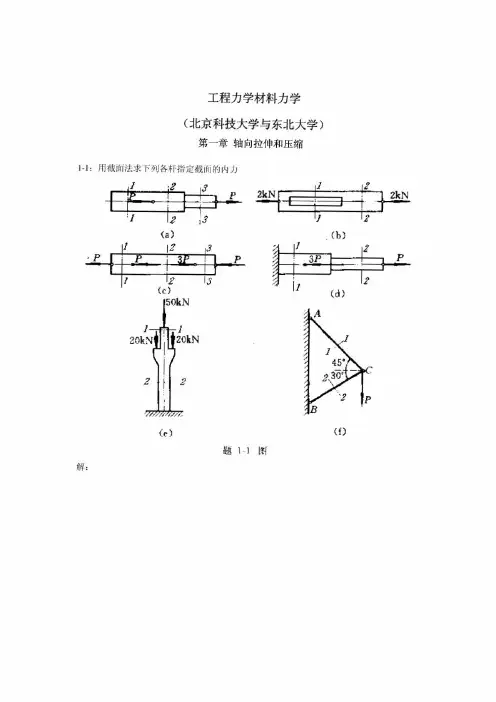

第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD,AD,AB(带滑轮C,重物E和一段绳索)的受力图。
1-4构架如图所示,试分别画出杆HED,杆BDC及杆AEC的受力图。
1-5构架如图所示,试分别画出杆BDH,杆AB,销钉A及整个系统的受力图。
1-6构架如图所示,试分别画出杆AEB,销钉A及整个系统的受力图。
1-7构架如图所示,试分别画出杆AEB,销钉C,销钉A及整个系统的受力图。
1-8结构如图所示,力P作用在销钉C上,试分别画出AC,BCE及DEH 部分的受力图。
参考答案1-1解:1-2解:1-3解:1-4解:1-5解:1-6解:1-7解:1-8解:第二章习题参考答案2-1解:由解析法,故:2-2解:即求此力系的合力,沿OB建立x坐标,由解析法,有故:方向沿OB。
2-3解:所有杆件均为二力杆件,受力沿直杆轴线。
(a)由平衡方程有:联立上二式,解得:(拉力)(压力)(b)由平衡方程有:联立上二式,解得:(拉力)(压力)(c)由平衡方程有:联立上二式,解得:(拉力)(压力)(d)由平衡方程有:联立上二式,解得:(拉力)(拉力)2-4解:(a)受力分析如图所示:由由(b)解:受力分析如图所示:由联立上二式,得:2-5解:几何法:系统受力如图所示三力汇交于点D,其封闭的力三角形如图示所以:(压力)(与X轴正向夹150度)2-6解:受力如图所示:已知,,由由2-7解:受力分析如图所示,取左半部分为研究对象由联立后,解得:由二力平衡定理2-8解:杆AB,AC均为二力杆,取A点平衡由联立上二式,解得:(受压)(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D,B点分别列平衡方程(1)取D点,列平衡方程由(2)取B点列平衡方程由2-10解:取B为研究对象:由取C为研究对象:由由联立上二式,且有解得:取E为研究对象:由故有:2-11解:取A点平衡:联立后可得:取D点平衡,取如图坐标系:由对称性及2-12解:整体受力交于O点,列O点平衡由联立上二式得:(压力)列C点平衡联立上二式得:(拉力)(压力)2-13解:(1)取DEH部分,对H点列平衡联立方程后解得:(2)取ABCE部分,对C点列平衡且联立上面各式得:(3)取BCE部分。
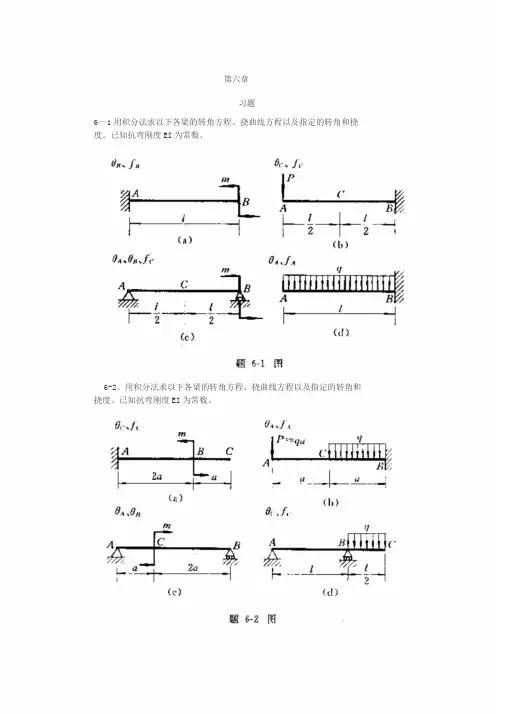
第六章习题6—1用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
m壁厚=4mm,单位长度重量6-7两端简支的输气管道,外径D=114m。
q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-845a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。
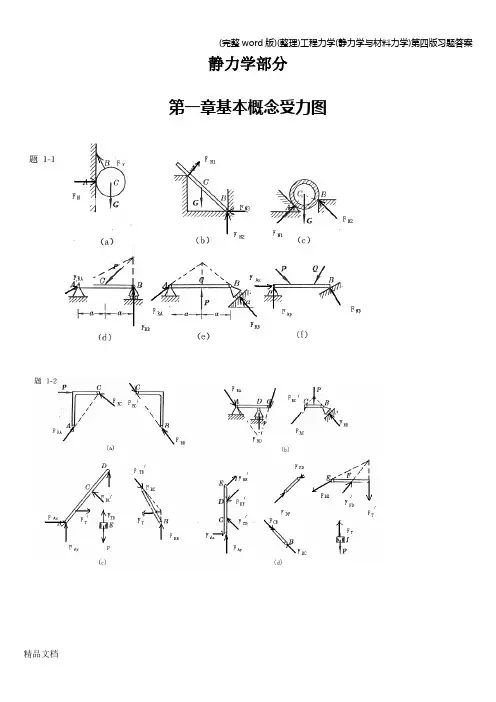
静力学部分第一章基本概念受力图2-1 解:由解析法,23cos 80RX F X P P Nθ==+=∑ 12sin 140RY F Y P P N θ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故:223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑ sin300ACAB FF -= 0Y =∑ cos300ACFW -=0.577AB F W =(拉力) 1.155AC F W =(压力)(b ) 由平衡方程有:0X =∑ cos700ACAB FF -= 0Y =∑ sin700ABFW -=1.064AB F W =(拉力)0.364AC F W =(压力)(c ) 由平衡方程有:0X =∑ cos60cos300ACAB FF -= 0Y =∑ sin30sin600ABAC FF W +-=0.5AB F W = (拉力)0.866AC F W =(压力)(d ) 由平衡方程有:0X =∑ sin30sin300ABAC FF -=0Y =∑ cos30cos300ABAC FF W +-=0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解:(a )受力分析如图所示:由x =∑22cos 45042RA F P -=+15.8RA F KN ∴=由Y =∑22sin 45042RA RB F F P +-=+7.1RB F KN ∴=(b)解:受力分析如图所示:由x =∑cos 45cos 45010RA RB F F P --= 0Y =∑sin 45sin 45010RA RB F F P +-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN = (压力) 5RB F KN =(与X 轴正向夹150度) 2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑ cos45cos450RA CB P F F --=0Y =∑ sin 45sin 450CBRA F F '-=联立后,解得: 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑ cos60cos300AC AB F F W ⋅--=0Y =∑ sin30sin600ABAC FF W +-=联立上二式,解得: 7.32AB F KN =-(受压)27.3AC F KN =(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑ sin cos 0DB T W αα-=0DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑ sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑ cos sin sin 0BC DC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BC BC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑ sin75sin750AB AD F F -=0Y =∑ cos75cos750ABAD FF P +-=联立后可得:2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑ cos5cos800AD ND F F '-=cos5cos80ND ADF F '=⋅由对称性及 AD AD F F '=cos5cos5222166.2cos80cos802cos75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O点,列O点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得: 2.92RAF KN=1.33DCF KN=(压力)列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得: 1.67ACF KN=(拉力)1.0BCF KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '-= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q2RE F Q '=(2)取ABCE 部分,对C 点列平衡x =∑ cos450RE RA F F -=0Y =∑ sin 450RBRA FF P --=且 RE RE F F '=联立上面各式得: 22RA F Q =2RB F Q P =+(3)取BCE 部分。

第六章 习题参考答案6-1解:(a )1()cos602Z M P P R P R =⋅⋅=⋅(b) 3()sin sin 602Z M P P R P R PRβ=-⋅⋅=-⋅⋅=-6-2解:sin 45cos 60sin 45212cos 45cos 60cos 45212sin 60520()0.242.4()0.50.268.4()0.0510.6X XY Y XY Z X Y Y Z X Z Y F F F N F F F N F F N M F F N mM F F F N m M F F N m=⋅=⋅==⋅=⋅====⨯=⋅=-⨯-⨯=-⋅=⨯=⋅6-3解:受力如图所示,为空间汇交力系。
0XF =∑cos 60cos30cos 60cos300AD BD F F -+=0YF =∑cos 60cos 60sin 30cos 60sin 30cos 600CD AD BD F F FG --+=0ZF=∑()sin 60sin 600AD BD CD F F F G G ++--=解得:31.5AD F KN=(压力)31.5BD F KN=(压力)1.5CD F KN=(压力)6-4解:受力分析如图所示,为空间汇交力系,由几何关系可得:2002OB OC mm ==;2003BD CD mm ==;5AD mm =XF =∑0335CD BD AD F F F --=YF =∑22032325CD BD AD F F F Q --= 0ZF=∑2203232CDBD F F -+= 解得:7.45AD F KN=-(压力)2.89BD F KN =(拉力)2.89CD F KN=(拉力)6-5解:受力分析如图所示:3F 和3F '构成一力偶,且有33F F '=0ZM=∑1122332220F r F r F r ⋅-⋅-⋅=1122333F r F r F F r ⋅-⋅'∴==6-6解:该平行力系的合力大小为:12345200()R RZ Z F F F P P P P P N ===++--=↑∑该合力RF 与平面的交点为(,C CX Y ),由合力矩定理有:12354()()13524650X R X M F M F P P P P P N cm==⨯+⨯+⨯-⨯-⨯=⋅∑1235()()43211200Y R Y M F M F P P P P KN==-⨯-⨯-⨯+⨯=-∑12006200Y C R M X cm F -∴=-=-=650 3.25200X C R M Y cm F ===6-7解:齿轮传动轴受力如图:0XF=∑120AX BX F R P F +++=0YF =∑0AY F =0ZF=∑120AZ BZ F P R F --+=0XM=∑121001502700BZ P R F -⨯-⨯+⨯=0Y M =∑12022P dP P -⨯+⨯=0zM=∑121001502700BX R P F -⨯-⨯-⨯=且有:1120R Ptg =2220R P tg =联立后解得: 12121950;3900;710;1420;P KN P KN R KN R KN ====2180;0;1860;AX AY AZ F N F F N =-==2430;1510BX BZ F N F N=-=6-8解:取轮I :0Y M =∑ 1102D m P '-⋅= 118713P P N'∴==111203172R Ptg Ptg N θ===取AB :0X F =∑120AX BX F F R R ++-=0ZF=∑120AZ BZ F F P P +--=0XM=∑212024375820AZ P P F -⨯-⨯+⨯=0Y M =∑3221022D D P P ⨯-⨯=0ZM=∑212024375820AX R R F ⨯-⨯-⨯=‘且有:2220R P tg=联立后解得:1.03;15.9AX AZ F KN F KN==5.64;19.8BX BZ F KN F KN==6-9解:0X F =∑12sin 20cos15cos150AX BX F N F S S -+--=0YF =∑0AY F =0ZF=∑12cos 20sin15sin150AZ BZ F N F S S +++-=0XM=∑12cos 20250500sin15650sin156500BZ N F S S ⨯+⨯+⨯-⨯=0Y M =∑12cos 20cos15cos150222d D DN S S -⨯+⨯-⨯=0ZM=∑12sin 20250500cos15650cos156500BX N F S S ⨯-⨯+⨯+⨯=联立后解得: 2130N N =500;0;919AX AY AZ F N F F N =-==-4130;1340BX BZ F N F N==-6-10(a )解:由对称性c x =11222705016530030152705030030105iicy A y A y A y A A mm+⨯⨯+⨯⨯===⨯+⨯=∑(b)解:由对称性 0c y =用负面积法求cx2107537.52007040210752007017.5iic x Ax Amm⨯⨯-⨯⨯==⨯-⨯=∑6-11解:由对称性 0c y =由减面积法求cx500560280400420320500560400420220iicx A x Amm⨯⨯-⨯⨯==⨯-⨯=∑6-12解:105002100105010501050500(2100)232100105010505000.51179i i c x A x A mm +⨯⨯+⨯⨯⨯+==⨯+⨯⨯=∑ 11050210010505251050500232100105010505000.5506i i c y A y A mm ⨯⨯+⨯⨯⨯==⨯+⨯⨯=∑ 6-13解:由对称性c y =由负面积法求cx2222()9.6iicx A R R r R a x AR r cmππππ⋅-⋅+==-=∑6-14解:受力分析如图所示0AM=∑()0N l W l b ⋅-⋅-=1.33Nlb l m W ∴=-=6-15解:由对称性,0c y =11223399...303 3.4595.6 5.178.6 4.0242.5 3.3885.5 2.632.51.6836.6 1.4356 1.7495.50.520.192930395.678.642.585.532.536.65695.5292.89i i keke C iZ A w z w z w z w z w z Awm ⋅+⋅++++==⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=+++++++++=∑∑。
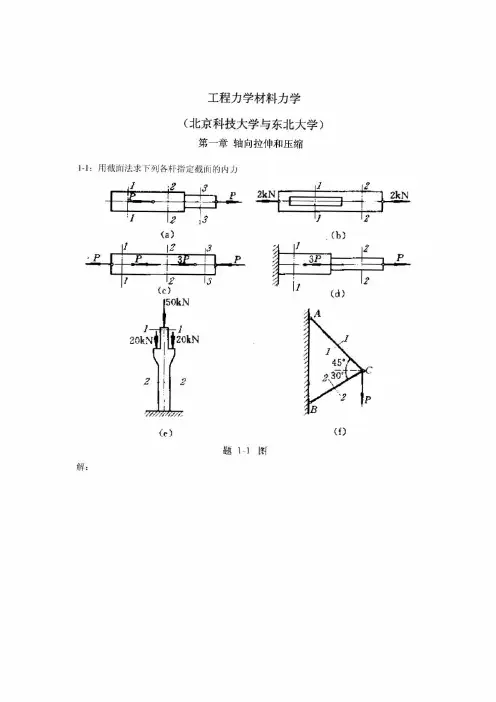

第六章习题6—1用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
m壁厚=4mm,单位长度重量6-7两端简支的输气管道,外径D=114m。
q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-845a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。

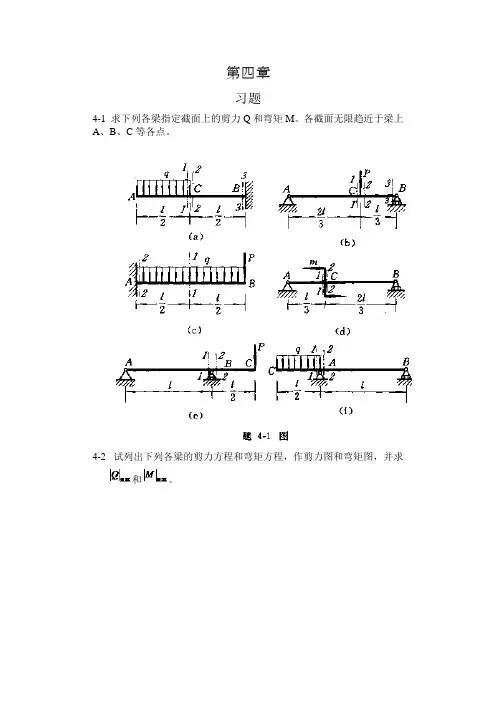
第四章习题4-1 求下列各梁指定截面上的剪力Q和弯矩M。
各截面无限趋近于梁上A、B、C等各点。
4-2 试列出下列各梁的剪力方程和弯矩方程,作剪力图和弯矩图,并求和。
4-3 用叠加法作以下各梁的弯矩图。
并求出。
4-4 用剪力、弯矩和分布载荷集度之间的微分关系校核前面已画的剪力图和弯矩图是否正确。
4-5 不列剪力方程和弯矩方程,作以下各梁的剪力图和弯矩图,并求出和。
4-6 用合适的方法作下列各梁的剪力图和弯矩图。
4-7 试根据载荷、剪力图和弯矩图之间的关系,检查下列各梁的剪力图和弯矩图是否正确,并对错误之处加以改正。
4-8 作下列构件的内力图。
4-9 在梁上行走的小车二轮的轮压均为P ,如图所示。
问小车行至何位置时梁内的弯矩最大?最大弯矩值是多少?设小车的轮距为c,大梁的跨度为。
参考答案4-1 解:题(b)(1)求支反力(见图)由,l-P l=0 =由,(2)剪力按计算剪力的规则(3)弯矩按计算弯矩的规则其它各题的答案:(a)(c)(d)(e)(f)4-2 解:题c(1)剪力和弯矩方程以左端A为原点,任一截面距左端的距离为x(图)\剪力方程:弯矩方程:(2 )剪力图与弯矩图按上述剪力方程和弯矩方程绘剪力图和弯矩图(3)与值由及得=200N =950题(f)(1)求支反力(见图)由,600-1004040=0=由,q4020-60=0=校核:+=2667+1333=4000N=q40=10040 所以支反力计算正确(2)剪力和弯矩方程以左端为原点,任一截面距左端的距离为x,则得剪力方程:弯矩方程(2)剪力图和弯矩图按上述剪力及弯矩方程绘出图及所示的剪力图和弯矩图所示剪力图和弯矩图.图中最大弯矩的截面位置可由,即剪力的条件求得Q(x)=3333-100x=0x=33.3cm(4)及由及得=2667N ,=355其他各题的答案:(a)=ql =(b)(d)(e)(g)(h)(i)(j)4-3 解:题c分别作、q单独作用时的弯矩图(图、),然后将此二图叠加得总的弯矩图。
静力学部分第一章基本概念受力图2-1 解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==o v v2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故:223R RX RY F F F KN=+= 方向沿OB 。
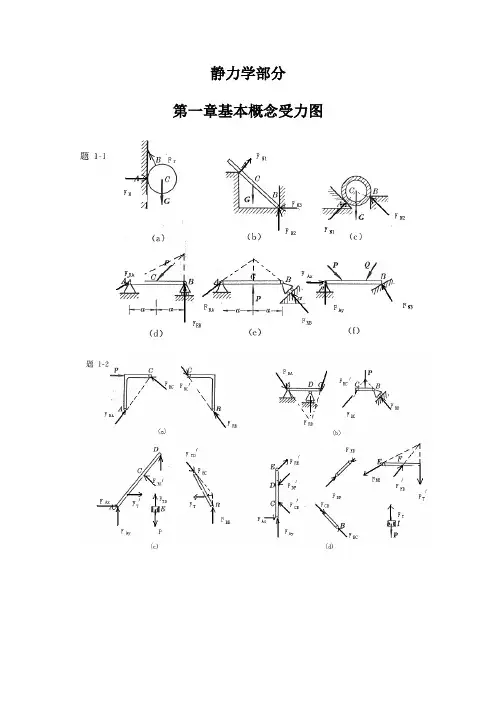
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a )由平衡方程有:0X =∑sin 300AC AB F F -=o0Y =∑cos300AC F W -=o0.577AB F W=(拉力)1.155AC F W=(压力)(b )由平衡方程有:0X =∑ cos 700AC AB F F -=o0Y =∑sin 700AB F W -=o1.064AB F W=(拉力)0.364AC F W=(压力)(c )由平衡方程有:0X =∑ cos 60cos300AC AB F F -=o o0Y =∑sin 30sin 600AB AC F F W +-=o o0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=o o0Y =∑cos30cos300AB AC F F W +-=o o0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+o15.8RA F KN∴=由0Y =∑22sin 45042RA RB F F P +-=+o7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑cos45cos 45010RA RB F F P ⋅--=o o0Y =∑sin 45sin 45010RA RB F F P ⋅+-=o o联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN= (压力) 5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CBRA F F '-=o o联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '=Q 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联立后可得:2cos 75AD AB PF F ==o取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=⋅oo由对称性及 ADAD F F '=cos5cos5222166.2cos80cos802cos 75N NDAD PF F F KN '∴===⋅=o o o o o2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q -=联立方程后解得:RD F =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
第四章习题4-1 求下列各梁指定截面上的剪力Q和弯矩M。
各截面无限趋近于梁上A、B、C等各点。
4-2 试列出下列各梁的剪力方程和弯矩方程,作剪力图和弯矩图,并求和。
4-3 用叠加法作以下各梁的弯矩图。
并求出。
4-4 用剪力、弯矩和分布载荷集度之间的微分关系校核前面已画的剪力图和弯矩图是否正确。
4-5 不列剪力方程和弯矩方程,作以下各梁的剪力图和弯矩图,并求出和。
4-6 用合适的方法作下列各梁的剪力图和弯矩图。
4-7 试根据载荷、剪力图和弯矩图之间的关系,检查下列各梁的剪力图和弯矩图是否正确,并对错误之处加以改正。
4-8 作下列构件的内力图。
4-9 在梁上行走的小车二轮的轮压均为P ,如图所示。
问小车行至何位置时梁内的弯矩最大?最大弯矩值是多少?设小车的轮距为c,大梁的跨度为。
参考答案4-1 解:题(b)(1)求支反力(见图)由,l-P l=0 =由,(2)剪力按计算剪力的规则(3)弯矩按计算弯矩的规则其它各题的答案:(a)(c)(d)(e)(f)4-2 解:题c(1)剪力和弯矩方程以左端A为原点,任一截面距左端的距离为x(图)\剪力方程:弯矩方程:(2 )剪力图与弯矩图按上述剪力方程和弯矩方程绘剪力图和弯矩图(3)与值由及得=200N =950题(f)(1)求支反力(见图)由,600-1004040=0=由,q4020-60=0=校核:+=2667+1333=4000N=q40=10040 所以支反力计算正确(2)剪力和弯矩方程以左端为原点,任一截面距左端的距离为x,则得剪力方程:弯矩方程(2)剪力图和弯矩图按上述剪力及弯矩方程绘出图及所示的剪力图和弯矩图所示剪力图和弯矩图.图中最大弯矩的截面位置可由,即剪力的条件求得Q(x)=3333-100x=0x=33.3cm(4)及由及得=2667N ,=355其他各题的答案:(a)=ql =(b)(d)(e)(g)(h)(i)(j)4-3 解:题c分别作、q单独作用时的弯矩图(图、),然后将此二图叠加得总的弯矩图。
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a 所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN ,吊杆的尺寸如图b 所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS=38.1MPa1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC ACLNL EA EA σε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析标准化文件发布号:(9312-EUATWW-MWUB-WUNN-INNUL-DDQTY-KII工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=,N2=注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==σ2=2228504P kN S d π= =∴σmax =1-3:试计算图a 所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN ,吊杆的尺寸如图b 所示。
解:下端螺孔截面:σ1=19020.065*0.045P S ==上端单螺孔截面:σ2=2PS =上端双螺孔截面:σ3= 3PS=∴σmax=1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=σBC=22FS= MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*=180mm2S2=(H-d)*t=(65-30)*=∴σmax=2FS=1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△l AC=NLEA=ACLEAσ=△l CD=CDL EAσ=0△L DB=DBL EA σ=(2) ∴AB l∆=1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127AC AC CB CB P MPa S P MPa S σσ====AC AC AC L NL EA EA σε===*104,CB CB CB L NL EA EA σε===*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:Nll EAl l ε∆=∆= ∴NEA ε=62.54*10N EA N ε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa 上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
第六章
习题
6—1 用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]
=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:
6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许
用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
6-7两端简支的输气管道,外径D=114mm。
壁厚=4mm,单位长度重量q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度
试确定管道的最大跨度。
6-8 45a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的
最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC 段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如
图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受
集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得
C端的挠度
6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,
梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。
试问当百分表F指针转动一小格(1/100mm)时,载荷P增加多少?
6-11试求以下各梁的支反力,并做弯矩图。
由图可见有三个支反力,但在平面能够力系中,只可列出二个静力平衡方程,可知此梁是静不定梁问题。
(1)选取静定基,建立变形条件
假想解除多余约束C,选取静定基如图(b),变形条件为(2)计算变形
(3)建立补充方程,解出多余反力
利用变形条件,可得补充方程
算出中间支座的反力,
(4)由平衡条件求其他支座反力
因为此梁的载荷和结构有对称性,可知
(5)作弯矩图如图c) 在中间支座处
6-12加热炉内的水管横梁,支持在三个支点上,承受纵管传来的钢锭载荷。
求A、B、C处的反力。
并作横梁的弯矩图。
提示:横管简化成三支点的静不定梁。
6-13在车床加工工件,已知工件的弹性模量E=220GP a,试问(1)按图(a)方式加工时,因工件而引起的直径误差是多少?
(2)如在工件自由端加上顶尖后,按车刀行至工作中点时考虑(b),这时因工件变形而引起的直径误差又是多少?(3)二
者误差的百分比如何?
提示:(a)情形可简化成在右端作用一集中力P的静定是悬臂梁,(b)情形可简化成左端固定右端简支的静不定梁,在中点作
用一集中力P。
计算直径的误差时,应是所求得挠度的二倍。
6-14、悬臂梁AB因强度和刚度不足,用同材料同截面的一根短梁AC加固,如图所示。
问(1)支座C处的反力为多
少?(2)梁AB的最大弯矩和最大挠度要比没有梁AC支撑时减少多少?
6-15、图示一铣床齿轮轴AB,已知传动功率,转速n=230rpm,D轮为主动轮。
若仅考虑齿轮切向力的影响,试求此
轴的弯矩图。
参考答案
6—1 解:(a)
挠曲线微分方程为:
积分得:
(1)
(2)
在固定端A,转角和挠度均应等于零,即:
当x=0时,;
把边界条件代入(1),(2)得
C=0
D=0
再将所得积分常数
(3)
(4)
求B点处转角和挠度
x=l时代入(3),(4)
(b)任意截面上的弯矩为:
挠曲线的微分方程:
积分得
(1)
(2)在固定端B
当x=0时
将边界条件代入(1)、(2)中,得:
C=D=0
再将所得积分常数C和D代回(1)、(2)式,得转角方程和挠曲线方程
以截面C的横坐标x=l/2代入以上两式,得截面C的转角和挠度分别为
(c)求支座反力:
=0
选取如图坐标,任意截面上的弯矩为:
挠曲线的微分方程为:
积分得:
(1)
(
2)
铰支座上的挠度等于零,故
x=0时
因为梁上的外力和边界条件都对跨度中点对称,挠曲线也对该点对称。
因此,在跨度中点,挠曲线切线的斜率
截面的转角都应等于零,即
x=时=0
分别代入(1)、(2)式,得
,D=0
以上两式代入(1)(2)得
当x=0时,
当x=l/2时,
6-2解:AC段,
(d)、
解:取坐标系如图。
(1)、求支坐反力、列弯矩方程
支座反力,
AB段,
BC段,
(2)列梁挠曲线近似微分方程并积分
AB段,
BC段,
(3)确定积分常数
利用边界条件:
处,,代入上面式中,得,
处,,再代入式中,得
处,,由和式可得。
处,,代入式中,得
(4)转角方程和挠度方程
AB段,
BC段,
最后指出,列弯矩方程时,不变,也可取截面右侧的载荷列
出,,这样可使计算大为简化。
6-3、解:(a)计算转角左、右集中力P分别为和表示集中力作用下引起的转角,
集中力作用下引起的转角,
所以
(1)计算挠度
集中力作用下引起的挠度,
集中力作用下引起的挠度
所以
答(b)
,
(c)(1) 计算转角
力偶作用下引起的转角
力P作用下引起的转角
所以
(2)、计算挠度
力偶作用下引起的挠度力P作用下引起的转角
所以
回答
(d ),
(e) ,
(f) 解答:
(1计算转角力P作用下引用的转角
力偶作用下引起的转角
所以
(2计算挠度力P作用下引起的挠度
力偶作用下引起的挠度
所以
6-5回答:
6-6解:(1)选择截面
采用迭加法可求得最大弯矩
由正应力强度条件可得
(2)校核刚度
采用迭加法可求得最大挠度
计算可知,此钢梁的刚度够。
6-7 答:
6-8 答:
6-9提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受
集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得
C端的挠度
6-11答:(b)
提示:题(c)在固定端处,除有反力偶及竖直反力外,还有水平反力,此梁是一次静不定梁。
可以解除支
座B,选择反力作多余反力,建立补充方程求解。
答:
答(d),在固定端。
6-12答:在距离两端的处。
6-13答:(1)二者误差百分比为2.73%
6-14解:(1)计算约束反力
根据在加固处两个悬臂梁的挠度相等这个变形条件,来计算约束反力。
即
可得
(2)比较最大弯矩
没有加固梁时,
有加固时,
比较可知,梁AB加固后,最大弯矩可减少一半。
(3)比较最大挠度
没有加固梁时,
有加固时,
经加固后,梁AB在右端的最大挠度要减少
6-15解:
(1)计算AB轴上的外力
AB轴上的外力偶矩
作用于AB轴的左右齿轮上的切向力为
(2)求AB轴上的约束反力
AB轴是一次静不定梁,取静定基如图(b),变形条件为而
代入有关数据,再代回变形条件中,可得
由平衡条件,
(3)作弯矩图
AB轴的弯矩图如图(c)。