2018年中考数学 第1编 教材知识梳理篇 第6章 图形的相似与解直角三角形 第18讲 相似(精练)试题(含答案)

第六章 图形的相似与解直角三角形第十八讲 相似,考标完全解读),感受宜宾中考)1．(2015宜宾中考)如图，△OAB 与△OCD 是以点O 为位似中心的位似图形，相似比为1∶2，∠OCD ＝90°，CO ＝CD.若B(1，0)，则点C的坐标为( B )A ．(1，2) B ．(1，1) C ．(2，2) D ．(2，1),(第1题图)) ,(第2题图))2．(2013宜宾中考改编)如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，CD ⊥AB 于点D.则△BCD 与△ABC 的周长之比为( A )A ．1∶2B . 1∶3C . 1∶4D . 1∶53．(2014宜宾中考改编)若一个图形的面积为2，那么将与它成中心对称的图形放大为原来的两倍后的图形面积为( A )A ．8B ．6C ．4D ．24．(2015宜宾中考模拟)如图，P 是Rt △ABC 斜边AB 上一点(A ，B 两点除外)，过点P 作一直线，使截得的三角形与Rt △ABC 相似，这样的直线可以作( C )A ．1条B . 2条C . 3条D . 4条,(第4题图)),(第5题图))5．(2017宜宾中考)如图，⊙O 的内接正五边形ABCDE 的对角线AD 与BE 相交于点G ，AE ＝2，则EG 的长是．,核心知识梳理)线段的比、线段成比例及比例的性质1．两条线段的比是两条线段的长度之比． (1)两条线段的长度单位需统一； (2)线段的比是一个不带单位的整数． 2．线段成比例，如a b ＝cd(即ad ＝bc)．对于四条线段a ，b ，c ，d ，如果其中两条线段的比与另外两条线段的比相等，我们就说这四条线段成比例． 3．比例的性质性质1：a b ＝cd ⇔ad ＝bc(bd≠0)；性质2：a b ＝c d 那么a ±b b ＝c ±dd；性质3：如果a b ＝c d ＝…＝m n (b ＋d ＋…＋n≠0)，则a ＋c ＋…＋m b ＋d ＋…＋n ＝a b ＝cd .4．黄金分割如果点C 把线段AB 分成两条线段，使AC AB ＝__BCAC __，那么点C 叫做线段AB 的__黄金分割点__，AC 是BC 与AB的比例中项，AC 与AB 的比叫做__黄金比__．相似三角形5．平行线分线段成比例 6．相似三角形的判定与性质(1)判定：①__有两角__对应相等，两三角形相似； ②两边对应成比例且__夹角__相等，两三角形相似； ③三边__对应成比例__，两三角形相似；④两直角三角形的斜边和一条直角边__对应成比例__，两直角三角形相似． 【方法点拨】判定三角形相似的几条思路： (1)条件中若有平行线，可采用相似三角形的判定；(2)条件中若有一对等角，可再找一对等角[用判定(1)]或再找夹边成比例[用判定(2)]； (3)条件中若有两边对应成比例，可找夹角相等；(4)条件中若有一对直角，可考虑再找一对等角或证明斜边、直角边对应成比例；(5)条件中若有等腰条件，可找顶角相等，可找一个底角相等，也可找底和腰对应成比例． (2)性质：①相似三角形的__对应角__相等；②相似三角形的对应线段(__边、高、中线、角平分线__)成比例； ③相似三角形的周长比等于__相似比__，面积比等于__相似比的平方__．相似多边形的判定及性质7．定义：对应角__相等__，对应边__成比例__的两个多边形叫做相似多边形，相似多边形对应边的比叫做它们的__相似比__．8．性质：(1)相似多边形的对应边__成比例__；(2)相似多边形的对应角__相等__；(3)相似多边形周长的比__于__相似比，相似多边形面积的比等于__相似比的平方__．位似图形9．定义：如果两个图形不仅是相似图形而且每组对应点所在的直线都经过同一个点，那么这样的两个图形叫做__位似图形__，这个点叫做__位似中心__，相似比叫做位似比．10．性质：(1)在平面直角坐标系中，如果位似变换是以原点为中心，相似比为k ，那么位似图形对应点的坐标的比等于__k 或－k__；(2)位似图形上任意一对对应点到位似中心的距离之比等于__位似比(或相似比)__．11．找位似中心的方法：将两个图形的各组对应点连接起来，若它们的直线或延长线相交于一点，则该点即是__位似中心__．12．画位似图形的步骤： (1)确定__位似中心__； (2)确定原图形的关键点；(3)确定__位似比__，即要将图形放大或缩小的倍数； (4)作出原图形中各关键点的对应点；(5)按原图形的连接顺序连接所作的各个对应点．,重点难点解析)线段成比例及比例的性质【例1】(1)若y x ＝34，则x ＋yx 的值为( )A ．1B .47C .54D .74(2)下列各组线段(单位：cm )中，成比例线段的是( )A ．1，2，4，8B ．2，4，6，8C ．3，6，8，12D ．3，6，9，12【解析】(1)∵y x ＝34，∴x ＋y x ＝4＋34＝74；(2)若在四条线段中，存在其中两条线段长度的比等于另外两条线段长度的比，则称这四条线段是成比例线段(或比例线段)，本题中只有选项A 中存在两条线段长度的比等于另外两条线段长度的比．【答案】(1)D ；(2)A 【针对训练】1．下列各组数中，成比例的是( A )A ．－6，－8，3，4B . －7，－5，14，5C . 3，5，9，12D . 2，3，6，122．如图，直线l 1∥l 2∥l 3，直线AC 分别交l 1，l 2，l 3于点A ，B ，C ；过点B 的直线DE 分别交l 1，l 3于点D ，E.若AB ＝2，BC ＝4，BD ＝1.5，则线段BE 的长为( C )A ．1B ．2C ．3D ．4位似变换【例2】如图，△ABC 三个顶点坐标分别为A(－1，3)，B(－1，1)，C(－3，2)．(1)请画出△ABC 关于y 轴对称的△A 1B 1C 1.(2)以原点O 为位似中心，将△A 1B 1C 1放大为原来的2倍，得到△A 2B 2C 2，请在第三象限内画出△A 2B 2C 2，并求出S △A 1B 1C 1∶S △A 2B 2C 2的值．【解析】(1)根据网格结构找出点A 、B 、C 关于x 轴的对称点A 1、B 1、C 1的位置，然后顺次连接即可得到△A 1B 1C 1；(2)连接A 1O 并延长至A 2，使A 2O ＝2A 1O ，连接B 1O 并延长至B 2，使B 2O ＝2B 1O ，连接C 1O 并延长至C 2，使C 2O ＝2C 1O ，然后顺次连接点A 2、B 2、C 2即可得到△A 2B 2C 2；由变换的方式可知△A 1B 1C 1与△A 2B 2C 2相似，且相似比为1∶2，根据相似三角形面积的比等于相似比的平方便可求出两个三角形的面积比．【答案】解：(1)△A 1B 1C 1如图所示；(2)△A 2B 2C 2如图所示．∵△A 1B 1C 1放大为原来的2倍得到△A 2B 2C 2， ∴△A 1B 1C 1∽△A 2B 2C 2，且相似比为1∶2， ∴S △A 1B 1C 1∶S △A 2B 2C 2＝1∶4. 【针对训练】3．如图，直线y ＝12x ＋1与x 轴交于点A ，与y 轴交于点B ，△BOC 与△B′O′C′是以点A 为位似中心的位似图形，且相似比为1∶3，求点B 的对应点B′的坐标．解：∵直线y ＝12x ＋1与x 轴交于点A ，与y 轴交于点B.令x ＝0，可得y ＝1， 令y ＝0，解得x ＝－2，∴点A 和点B 的坐标分别为(－2，0)，(0，1)．∵△BOC 与△B′O′C′是以点A 为位似中心的位似图形，且相似比为1∶3， ∴OB O ′B ′＝OA AO ′＝13，∴O ′B ′＝3，AO ′＝6， ∴B ′的坐标为(－8，－3)或(4，3)．相似三角形的性质和判定【例3】如图，在平行四边形ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF ∶FC 等于( )A ．3∶2B ．3∶1C . 1∶1D ．1∶2【解析】根据题意得出△DEF∽△BCF，DE BC ＝EFFC ，利用点E 是边AD 的中点得出答案即可．【答案】D 【针对训练】4．如图，在△ABC 中，D ，E 分别为AB ，AC 边上的点，DE ∥BC ，BE 与CD 相交于点F ，则下列结论一定正确的是( A )A .AD AB ＝AE AC B .DF FC ＝AE EC C .AD DB ＝DE BCD .DF BF ＝EF FC相似三角形知识的综合应用在中考题目中，相似三角形的知识常与解直角三角形、全等三角形、圆、二次函数等知识综合，考查考生探索问题、解决问题的能力．【例4】如图，在直角坐标系中，Rt △OAB 的直角顶点A 在x 轴上，OA ＝4，AB ＝3.动点M 从点A 出发，以每秒1个单位长度的速度，沿AO 向终点O 移动；同时点N 从点O 出发，以每秒1.25个单位长度的速度，沿OB 向终点B 移动．当两个动点运动了x s (0<x<4)时，解答下列问题：(1)求点N 的坐标；(用含x 的代数式表示)(2)设△OMN 的面积是S ，求S 与x 之间的函数表达式；当x 为何值时，S 有最大值？最大值是多少？ (3)在两个动点运动过程中，是否存在某一时刻，使△OMN 是直角三角形？若存在，求出x 的值；若不存在，请说明理由．【解析】(1)由勾股定理求出OB ，作NP⊥OA 于P ，则NP∥AB，得出△OPN∽△OAB，得出比例式，求出OP 、PN ，即可得出点N 的坐标；(2)由三角形的面积公式得出S 是x 的二次函数，即可得出S 的最大值；(3)分两种情况：①若∠OMN＝90°，则MN∥AB，由平行线得出△OMN∽△OAB，得出比例式，即可求出x 的值；②若∠ONM＝90°，则∠ONM＝∠OAB，证出△OMN∽△OBA，得出比例式，求出x 的值即可．【答案】解：(1)根据题意得：MA ＝x ，ON ＝1.25x ， 在Rt △OAB 中，由勾股定理得：OB 2＝OA 2＋AB 2， OB ＝OA 2＋AB 2＝42＋32＝5，作NP⊥OA 于P ，如图①所示， 则NP∥AB， ∴△OPN ∽△OAB ， ∴PN AB ＝OP OA ＝ON OB ， 即PN 3＝OP 4＝1.25x 5， 解得OP ＝x ，PN ＝34x ，∴点N 的坐标是⎝ ⎛⎭⎪⎫x ，34x ； (2)在△OMN 中，OM ＝4－x ，OM 边上的高PN ＝34x ，∴S ＝12OM ·PN ＝12(4－x)·34x ＝－38x 2＋32x ，∴S ＝－38x 2＋32x(0<x<4)，即S ＝－38(x －2)2＋32.当x ＝2时，S 有最大值，最大值是1.5；(3)存在某一时刻，使△OMN 是直角三角形，理由如下： 分两种情况：①若∠OMN＝90°，如图②所示， 则MN∥AB，此时OM ＝4－x ，ON ＝1.25x ， ∵MN ∥AB ， ∴△OMN ∽△OAB ， ∴OM OA ＝ON OB ，即4－x 4＝1.25x 5， 解得x ＝2；②若∠ONM＝90°，如图③所示，则∠ONM＝∠OAB，此时OM ＝4－x ，ON ＝1.25x ， ∵∠ONM ＝∠OAB， ∠MON ＝∠BOA， ∴△OMN ∽△OBA ， ∴OM OB ＝ON OA ，即4－x 5＝1.25x 4， 解得x ＝6441.综上所述，x 的值是2或6441 s 时，△OMN 是直角三角形．【针对训练】5．(2017恩施中考)如图，在△ABC 中，DE ∥BC ，∠ADE ＝∠EFC，AD ∶BD ＝5∶3，CF ＝6，则DE 的长为( C )A ．6B ．8C ．10D ．12,(第5题图)) ,(第6题图))6．(2017泰安中考)如图，正方形ABCD 中，M 为BC 上一点，ME ⊥AM ，ME 交AD 的延长线于点E.若AB ＝12，BM ＝5，则DE 的长为( B )A ．18B .1095 C .965 D .253,当堂过关检测)1.已知a b ＝34，b c ＝35，则a∶b∶c 等于( C )A ．3∶4∶5B ．4∶3∶5C ．9∶12∶20D ．9∶15∶202．在下列命题中，真命题是( D )A ．两个钝角三角形一定相似B ．两个等腰三角形一定相似C ．两个直角三角形一定相似D ．两个等边三角形一定相似3．(2017滨州中考)在平面直角坐标系中，点C ，D 的坐标分别为C(2，3)，D(1，0)．现以原点为位似中心，将线段CD 放大得到线段AB ，若点D 的对应点B 在x 轴上且OB ＝2，则点C 的对应点A 的坐标为__(4，6)或(－4，－6)__．4．(2017六盘水中考)如图，在平行四边形ABCD 中，对角线AC ，BD 相交于点O ，在BA 的延长线上取一点E ，连结OE 交AD 于点F ，若CD ＝5，BC ＝8，AE ＝2，则AF ＝__169__.5．梯形的中位线长为12 cm ，上、下底之比为1∶3，则梯形的上、下底之差是__－12______．6．(2017沈阳中考)如图，在矩形ABCD 中，AB ＝5，BC ＝3，将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ，点A 落在矩形ABCD 的边CD 上，连接CE ，则CE 的长是5。

第六章《图形的相似》知识点一：比例线段1.比例线段：在四条线段a ，b ，c ，d 中，如果a 与b 的比等于c 与d 的比，即a cb d=，那么这四条线段a ，b ，c ，d 叫做成比例线段，简称比例线段． 2.比例的基本性质：(1)基本性质：a cb d =⇔ ad ＝bc ；（b 、d ≠0）(2)合比性质：a c b d =⇔a b b ±＝c dd±；（b 、d ≠0） (3)等比性质：a cb d =＝…＝m n ＝k (b ＋d ＋…＋n ≠0)⇔......a c mb d n++++++＝k .（b+d …+n ≠0） 3.平行线分线段成比例定理：（1）两条直线被一组平行线所截，所得的对应线段成比例.即如图所示，若l 3∥l 4∥l 5，则AB DEBC EF=.（2）平行于三角形一边的直线截其他两边(或两边的延长 线)，所得的对应线段成比例.即如图所示，若AB ∥CD ，则OA OBOD OC=. （3）平行于三角形一边的直线和其他两边相交，所构成的三角形和原三角形相似． 如图所示，若DE ∥BC ，则△ADE ∽△ABC.4. 黄金分割：点C 把线段AB 分成两条线段AC 和BC ，如果AC AB ＝=5－12≈0.618，那么线段AB 被点C 黄金分割．其中点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比．例1：把长为10cm 的线段进行黄金分割，那么较长线段长为 cm 。

知识点二 ：相似三角形的性质与判定5. 相似三角形的判定：(1) 两角对应相等的两个三角形相似(AAA).如图，若∠A ＝∠D ，∠B ＝∠E ，则△ABC ∽△DEF. (2) 两边对应成比例，且夹角相等的两个三角形相似． 如图，若∠A ＝∠D ，AC ABDF DE=，则△ABC ∽△DEF. FE DC B A学 班级 姓名 考试号-----------------------------------------------------------密---------------------------------封----------------------------------线--------------------------------------(3) 三边对应成比例的两个三角形相似．如图，若AB AC BCDE DF EF==，则△ABC∽△DEF.6.相似三角形的性质：(1)对应角相等，对应边成比例．(2)周长之比等于相似比，面积之比等于相似比的平方．(3)相似三角形对应高的比、对应角平分线的比和对应中线的比等于相似比．例2：(1)已知△ABC∽△DEF，△ABC的周长为3，△DEF的周长为2，则△ABC与△DEF的面积之比为 .(2) 如图，DE∥BC， AF⊥BC,已知S△ADE:S△ABC=1:4，则AF:AG= .【学习目标】1.加深了解比例的基本性质、线段的比、成比例线段，认识图形的相似、位似等概念和性质．2.理解相似图形的性质与判定、位似的性质与把一个图形放大或缩小，在同一坐标系下感受位似变换后点的坐标的变化规律.【重点难点】重点：利用相似三角形知识解决实际的问题；位似的应用及在平面直角坐标系中作位似图形．难点：如何把实际问题抽象为相似三角形、位似形这一数学模型.【知识回顾】1、相似三角形定义：_________________________．2、判定方法：__________________________3、相似三角形性质：（1）对应角相等，对应边成比例；（2）对应线段之比等于；（对应线段包括哪几种主要线段？）（3）周长之比等于；（4）面积之比等于．4、相似三角形中的基本图形．（1）平行型（X型，A型）; （2）交错型；（3）旋转型；（4）母子三角形.5、位似形的性质： .6、将一个图形按一定的比例放大或缩小的步骤为： . 【综合运用】1.如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.（1）求证：△ADF∽△DEC（2）若AB＝4,AD＝33,AE＝3,求AF的长.2如图，在等腰三角形△ABC中，底边BC=60cm，高AD=40cm，四边形PQRS是正方形，S,R分别在AB,AC上，SR与AD相交于点E.（1）△ASR与△ABC相似吗？为什么？（2）求正方形PQRS的边长.【矫正补偿】如图1，已知矩形ABED，点C是边DE的中点，且AB = 2AD．（1）判断△ABC的形状，并说明理由；（2）保持图1中ABC固定不变，绕点C旋转DE所在的直线MN到图2中（当垂线段AD、BE在直线MN的同侧），试探究线段AD、BE、DE长度之间有什么关系？并给予证明．【完善整合】1.通过本节课的学习你有那些收获?2.你还有哪些疑惑？第六章《图形的相似》易错疑难易错点1 对黄金分割的概念理解不清而出现漏解AB ，点C是线段AB的黄金分割点，则AC的长为.1. 已知线段20易错点2 找不准三角形的对应关系2. 如图，ACD ∆和ABC ∆相似需具备的条件是() A.AC AB CD BC =； B. CD BCAD AC=C. 2AC AD AB =g ；D. 2CD AD BD =g易错点3 混淆相似三角形的性质，误认为相似三角形的面积比等于相似比 3. 如图，若ADE ABC ∆∆:，DE 与AB 相交于点D ，与AC 相交于点E ，2DE =，5BC =，20ABC S ∆=，求ADE S ∆的值.易错点4 不能区分“相似”写“:”的含义4. 如图，在矩形ABCD 中，10,4AB AD ==，点P 是边AB 上一点，连接,PD PC ，若APD ∆与BPC ∆相似，则满足条件的点P 有 个.第4题第5题5. 如图，ABC ∆中，90C ∠=︒，16BC =cm ，12AC =cm ，点P 从点B 出发，沿BC 以2 cm/s 的速度向点C 移动，点Q 从点C 出发，以1 cm/s 的速度向点A 移动，若点,P Q 分别从点,B C 同时出发，设运动时间为t s ，当t = 时，CPQ ∆与CBA ∆相似. 疑难点1 相似三角形的判定和性质的综合应用1. 如图是一块含30°角的直角三角板，它的斜边8AB =8cm ，里面空心DEF ∆的各边与ABC ∆的对应边平行，且各对应边间的距离都是1 cm ，那么DEF ∆的周长是( )A. 5cm ；B. 6cm ；C. (63)-cm ；D. (33)+cm第1题第2题2. 如图，已知矩形ABCD ，2,6AB BC ==，点E 从点D 出发，沿DA 方向以每秒1个单位长度的速度向点A 运动，点F 从点B 出发，沿射线AB 以每秒3个单位长度的速度运动，当点E 运动到点A 时，,E F 两点停止运动.连接BD ，过点E 作EH BD ⊥，垂足为H ，连接EF ，交BD 于点G ，交BC 于点M ，连接,CF EC .给出下列结论:①CDE CBF ∆∆:;②DBC EFC ∠=∠;③DE HGAB EH=;④GH 10.上述结论正确的个数为( )A.1B. 2C. 3D. 4 疑难点2 相似图形中的规律探索3.如图，在平面直角坐标系中，矩形AOCB 的两边,OA OC 分别在x 轴和y 轴上，且2,1OA OC ==.在第二象限内，将矩形AOCB 以原点O 为位似中心放大为原来的32倍，得到矩形111A OC B ，再将矩形111A OC B 以原点O 为位似中心放大32倍，得到矩形222A OC B ……依此类推，得到的矩形n n n A OC B 的对角线交点的坐标为 .第3题 第4题4.如图，已知正方形11ABC D 的边长为1，延长11C D 到1A ，以11A C 为边向右作正方形1122AC C D ，延长22C D 到2A ，以22A C 为边向右作正方形2233A C C D ……依此类推，若112A C =，且点12310,,,,,A D D D D …都在同一直线上，则正方形991010A C C D 的边长是 .疑难点3 相似三角形与函数等知识的综合5. 反比例函数y ＝的图象在第一象限的分支上有一点A （3，4），P 为x 轴正半轴上的一个动点，（1）求反比例函数解析式．（2）当P 在什么位置时，△OP A 为直角三角形，求出此时P 点的坐标．疑难点4 动态问题中的相似三角形6.如图，在直角坐标系中，点(0,4),(3,4),(6,0)A B C --，动点P 从点A 出发以1个单位长度/秒的速度在y 轴上向下运动，动点Q 同时从点C 出发以2个单位长度/秒的速度在x 轴上向右运动，过点P 作PD y ⊥轴，交OB 于点D ，连接DQ .当点P 与点O 重合时，两动点均停止运动.设运动的时间为t 秒.(1)当1t =时，求线段DP 的长;(2)连接CD ，设CDQ ∆的面积为S ，求S 关于t 的函数表达式，并求出S 的最大值; (3)运动过程中是否存在某一时刻，使ODQ ∆与ABC ∆相似?若存在，请求出所有满足要求的t 的值;若不存在，请说明理由参考答案例1. 5(5－1)；例 2.（1）9：4；（2）1：2 综合运用：1.分析：（1）根据平行四边形的性质可得AD ∥BC ，AB ∥CD ，即得∠ADF =∠CED ，∠B +∠C =180°，再由∠AFE +∠AFD =180°，∠AFE =∠B ，可得∠AFD =∠C ，问题得证； （2）根据平行四边形的性质可得AD ∥BC ，CD =AB =4，再根据勾股定理可求得DE 的长，再由△ADF ∽△DEC 根据相似三角形的性质求解即可. 证明：（1）∵四边形ABCD 是平行四边形∴AD ∥BC ，AB ∥CD ∴∠ADF =∠CED ，∠B +∠C =180°∵∠AFE +∠AFD =180，∠AFE =∠B ∴∠AFD =∠C ∴△ADF ∽△DEC ； 解：（2）∵四边形ABCD 是平行四边形，∴AD ∥BC ，CD =AB =4。

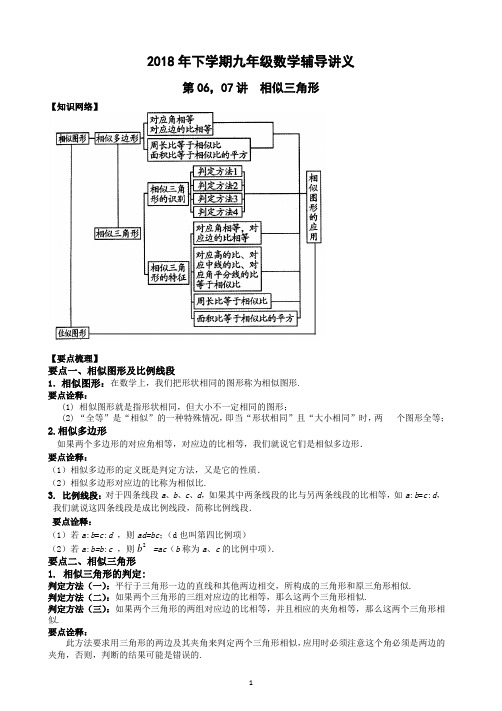
2018年下学期九年级数学辅导讲义第06，07讲 相似三角形【知识网络】【要点梳理】要点一、相似图形及比例线段1．相似图形：在数学上，我们把形状相同的图形称为相似图形.要点诠释：(1) 相似图形就是指形状相同，但大小不一定相同的图形； (2) “全等”是“相似”的一种特殊情况，即当“形状相同”且“大小相同”时，两 个图形全等；2.相似多边形如果两个多边形的对应角相等，对应边的比相等，我们就说它们是相似多边形． 要点诠释：（1）相似多边形的定义既是判定方法，又是它的性质． （2）相似多边形对应边的比称为相似比.3. 比例线段：对于四条线段a 、b 、c 、d ，如果其中两条线段的比与另两条线段的比相等，如a :b =c :d ，我们就说这四条线段是成比例线段，简称比例线段． 要点诠释：（1）若a :b =c :d ，则ad=bc ；（d 也叫第四比例项） （2）若a :b=b :c ，则 =ac （b 称为a 、c 的比例中项）．要点二、相似三角形 1. 相似三角形的判定:判定方法（一）：平行于三角形一边的直线和其他两边相交，所构成的三角形和原三角形相似. 判定方法（二）：如果两个三角形的三组对应边的比相等，那么这两个三角形相似. 判定方法（三）：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似.要点诠释：此方法要求用三角形的两边及其夹角来判定两个三角形相似，应用时必须注意这个角必须是两边的夹角，否则，判断的结果可能是错误的.2b判定方法（四）：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似. 判定方法（五）：如果两个直角三角形斜边与一条直角边对应成比例，那么这两个直角三角形相似. 要点诠释：要判定两个三角形是否相似，只需找到这两个三角形的两个对应角相等即可，对于直角三角形而言，若有一个锐角对应相等，那么这两个三角形相似.2. 相似三角形的性质：（1）相似三角形的对应角相等，对应边的比相等； （2）相似三角形中的重要线段的比等于相似比；相似三角形对应高，对应中线，对应角平分线的比都等于相似比. 要点诠释：要特别注意“对应”两个字，在应用时，要注意找准对应线段. (3) 相似三角形周长的比等于相似比；（4）相似三角形面积的比等于相似比的平方。

初中数学相似三角形知识点
学习可以这样来看，它是一个潜移默化、厚积薄发的过程。

小编编辑了初中数学相似三角形知识点，希望对您有所帮助!更多相关信息请关注相应栏目！
1.相似三角形定义：
对应角相等，对应边成比例的三角形，叫做相似三角形。

2.相似三角形的表示方法：用符号"∽"表示，读作"相似于"。

3.相似三角形的相似比：
相似三角形的对应边的比叫做相似比。

4.相似三角形的预备定理：
平行于三角形一边的直线和其他两边(或两边的延长线)相交，所截成的三角形与原三角形相似。

从表中可以看出只要将全等三角形判定定理中的"对应边相等"的条件改为"对应边
成比例"就可得到相似三角形的判定定理，这就是我们数学中的用类比的方法，在旧知识的基础上找出新知识并从中探究新知识掌握的方法。

6.直角三角形相似：
(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。

(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。

7.相似三角形的*质定理：
(1)相似三角形的对应角相等。

(2)相似三角形的对应边成比例。

(3)相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比。

(4)相似三角形的周长比等于相似比。

(5)相似三角形的面积比等于相似比的平方。

8.相似三角形的传递*
如果△abc∽△a1b1c1，△a1b1c1∽△a2b2c2，那么△abc∽a2b2c2。

图形的相似考点一、比例线段 1、比例线段的相关概念如果选用同一长度单位量得两条线段a ，b 的长度分别为m ，n ，那么就说这两条线段的比是，或写成a ：b=m ：n在两条线段的比a ：b 中，a 叫做比的前项，b 叫做比的后项。

在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫做成比例线段，简称比例线段若四条a ，b ，c ，d 满足或a ：b=c ：d ，那么a ，b ，c ，d 叫做组成比例的项，线段a ，d 叫做比例外项，线段b ，c 叫做比例内项，线段的d 叫做a ，b ，c 的第四比例项。

如果作为比例内项的是两条相同的线段，即cb b a =或a ：b=b ：c ，那么线段b 叫做线段a ，c 的比例中项。

2、比例的性质（1）基本性质①a ：b=c ：d ⇔ad=bc ②a ：b=b ：c ac b =⇔2（2）更比性质（交换比例的内项或外项） db c a =（交换内项）⇒=dcb a ac bd =（交换外项）abc d =（同时交换内项和外项） （3）反比性质（交换比的前项、后项）：cd a b d c b a =⇒= （4）合比性质：ddc b b ad c b a ±=±⇒= （5）等比性质：ban f d b m e c a n f d b n m f e d c b a =++++++++⇒≠++++==== )0( 3、黄金分割把线段AB 分成两条线段AC ，BC （AC>BC ），并且使AC 是AB 和BC 的比例中项，叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AC=215-AB ≈0.618AB 考点二、平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例。

nm b a =d c b a =推论：（1）平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例。

逆定理：如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边。

第五章 图形的相似与解直角三角形第一节 图形的相似与位似1．如图，在△ABC 中，∠C ＝90°，BC ＝6，D ，E 分别在AB ，AC 上，将△ABC 沿DE 折叠，使点A 落在点A′处，若A′为CE 的中点，则折痕DE 的长为( B )A .12B ．2C ．3D ．4(第1题图)(第2题图)2．(2017泰安中考)如图，正方形ABCD 中，M 为BC 上一点，ME ⊥AM ，ME 交AD 的延长线于点E.若AB ＝12，BM ＝5，则DE 的长为( B )A ．18B .1095 C .965 D .2533．(2017遵义十九中一模)如图，点P 在△ABC 的边AC 上，要判断△ABP∽△ACB，添加一个条件，不正确的是( D )A ．∠ABP ＝∠CB ．∠APB ＝∠ABC C .AP AB ＝ABACD .AB BP ＝AC CB(第3题图)(第4题图)4．(济南中考)如图，正方形ABCD 的对角线AC 与BD 相交于点O ，∠ACB 的平分线分别交AB ，DB 于M ，N 两点．若AM ＝2，则线段ON 的长为( C )A .22 B .32 C ．1 D .625．(2017滨州中考)在平面直角坐标系中，点C ，D 的坐标分别为C(2，3)，D(1，0)．现以原点为位似中心，将线段CD 放大得到线段AB ，若点D 的对应点B 在x 轴上且OB ＝2，则点C 的对应点A 的坐标为__(4，6)或(－4，－6)__．6．(2017随州中考)在△ABC 中，AB ＝6，AC ＝5，点D 在边AB 上，且AD ＝2，点E 在边AC 上，当AE ＝__125或53__时，以A ，D ，E 为顶点的三角形与△ABC 相似． 7．(汇川升学一模)如图，正方形DEFG 的边EF 在△ABC 的边BC 上，顶点D ，G 分别在边AB ，AC 上．若△ABC 的边BC 长为40 cm ，高AH 为30 cm ，则正方形DEFG 的边长为__1207__cm .(第7题图)(第8题图)8．(2017包头中考)如图，在平面直角坐标系中，Rt △ABO 的顶点O 与原点重合，顶点B 在x 轴上，∠ABO ＝90°，OA 与反比例函数y ＝kx 的图象交于点D ，且OD ＝2AD ，过点D 作x 轴的垂线交x 轴于点C.若S 四边形ABCD ＝10，则k 的值为__－16__．9．(2017六盘水中考)如图，在平行四边形ABCD 中，对角线AC ，BD 相交于点O ，在BA 的延长线上取一点E ，连接OE 交AD 于点F ，若CD ＝5，BC ＝8，AE ＝2，则AF ＝__169__．10．(泰安中考)如图，在△ABC 中，AB ＝AC ，点P ，D 分别是BC ，AC 边上的点，且∠APD＝∠B.(1)求证：AC·CD＝CP·BP；(2)若AB ＝10，BC ＝12，当PD∥AB 时，求BP 的长． 解：(1)∵AB＝AC ， ∴∠B ＝∠C.∵∠APD ＝∠B， ∴∠APD ＝∠B＝∠C. ∵∠APC ＝∠BAP＋∠B， ∠APC ＝∠APD＋∠DPC， ∴∠BAP ＝∠DPC， ∴△ABP ∽△PCD ， ∴BP CD ＝AB CP， ∴AB ·CD ＝CP·BP. ∵AB ＝AC ， ∴AC ·CD ＝CP·BP；(2)∵PD∥AB，∴∠APD ＝∠BAP. ∵∠APD ＝∠C ，∴∠BAP ＝∠C. ∵∠B ＝∠B，∴△BAP ∽△BCA ， ∴BA BC ＝BP BA. ∵AB ＝10，BC ＝12， ∴1012＝BP 10，∴BP ＝253.11．(随州中考)如图，D ，E 分别是△ABC 的边AB ，BC 上的点，且DE∥AC，AE ，CD 相交于点O ，若S △DOE ∶S △COA ＝1∶25，则S △BDE 与S △CDE 的比是( B )A ．1∶3B ．1∶4C ．1∶5D ．1∶2512．(盘锦中考)如图，四边形ABCD 是矩形，点E 和点F 是矩形ABCD 外两点，AE ⊥CF 于点H ，AD ＝3，DC ＝4，DE ＝52，∠EDF ＝90°，则DF 长是( C )A .158B .113C .103D .165(第12题图)(第13题图)13．(2017杭州中考)如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝15，AC ＝20，点D 在边AC 上，AD ＝5，DE ⊥BC 于点E ，连接AE ，则△ABE 的面积等于__78__.14.(2017长春中考)如图，在▱ABCD 中，点E 在边BC 上，点F 在边AD 的延长线上，且DF ＝BE ，EF 与CD 交于点G. (1)求证：BD∥EF；(2)若DG GC ＝23，BE ＝4，求EC 的长．解：(1)∵四边形ABCD 是平行四边形， ∴AD ∥BC. ∵DF ＝BE ，∴四边形BEFD 是平行四边形， ∴BD ∥EF ；(2)∵四边形BEFD 是平行四边形， ∴DF ＝BE ＝4. ∵DF ∥EC ， ∴△DFG ∽△CEG ， ∴DG CG ＝DF CE， ∴CE＝DF·CG DG ＝4×32＝6.15.(2017杭州中考)如图，在锐角三角形ABC 中，点D ，E 分别在边AC ，AB 上，AG ⊥BC 于点G ，AF ⊥DE 于点F ，∠EAF ＝∠GAC.(1)求证：△ADE∽△ABC； (2)若AD ＝3，AB ＝5，求AFAG 的值．解：(1)∵AG⊥BC，AF ⊥DE ， ∴∠AFE ＝∠AGC＝90°.∵∠EAF ＝∠GAC，∴∠AED ＝∠ACB， ∵∠EAD ＝∠BAC，∴△ADE ∽△ABC ； (2)由(1)可知：△ADE∽△ABC，∴AD AB ＝AE AC ＝35. ∵∠AFE ＝∠AGC＝90°，∠EAF ＝∠GAC， ∴△EAF ∽△CAG ， ∴AF AG ＝AE AC ， ∴AF AG ＝35. 16 .(2017枣庄中考)如图，在平面直角坐标系中，已知△ABC 三个顶点的坐标分别是A(2，2)，B(4，0)，C(4，－4)．(1)请在图中，画出△ABC 向左平移6个单位长度后得到的△A 1B 1C 1；(2)以点O 为位似中心，将△ABC 缩小为原来的12，得到△A 2B 2C 2，请在图中y 轴右侧，画出△A 2B 2C 2，并求出∠A 2C 2B 2的正弦值．解：(1)如图所示，△A 1B 1C 1即为所求； (2)如图所示，△A 2B 2C 2即为所求， 由图形可知，∠A 2C 2B 2＝∠ACB， 过点A 作AD⊥BC 交BC 的延长线于点D ，由A(2，2)，C(4，－4)，B(4，0)，易得D(4，2)， ∴AD ＝2，CD ＝6，AC ＝22＋62＝210， ∴sin ∠ACB ＝AD AC ＝2210＝1010，即sin ∠A 2C 2B 2＝1010.17．(2017连云港中考)如图，在△ABC 中，∠ABC ＝90°，BC ＝3，D 为AC 延长线上一点，AC ＝3CD ，过点D 作DH∥AB，交BC 的延长线于点H. (1)求BD·cos ∠HBD 的值； (2)若∠CBD＝∠A，求AB 的长． 解：(1)∵DH∥AB，∴∠BHD ＝∠ABC＝90°，∠A ＝∠HDC， ∴△ABC ∽△DHC ， ∴AC CD ＝BCCH＝3， ∴CH ＝1，BH ＝BC ＋CH ＝4， 在Rt △BHD 中，cos ∠HBD ＝BHBD ，∴BD ·cos ∠HBD ＝BH ＝4； (2)∵∠CBD＝∠A，∠ABC ＝∠BHD， ∴△ABC ∽△BHD ， ∴BC HD ＝AB BH. ∵△ABC ∽△DHC ， ∴AB DH ＝ACCD＝3， ∴AB ＝3DH ， ∴3DH ＝3DH4，解得DH ＝2， ∴AB ＝3DH ＝3×2＝6.18．(2017眉山中考)如图，△ABC 和△BEC 均为等腰直角三角形，且∠ACB ＝∠BEC＝90°，AC ＝42，点P 为线段BE 延长线上一点，连接CP ，以CP 为直角边向下作等腰直角△CPD，线段BE 与CD 相交于点F.(1)求证：PC CD ＝CECB；(2)连接BD ，请你判断AC 与BD 有什么位置关系？并说明理由； (3)设PE ＝x ，△PBD 的面积为S ，求S 与x 之间的函数关系式． 解：(1)∵△BCE 和△CDP 均为等腰直角三角形， ∴∠ECB ＝∠PCD＝45°， ∠CEB ＝∠CPD＝90°， ∴△BCE ∽△DCP ，∴PC DC ＝EC CB； (2)AC∥BD.理由如下：∵∠PCE ＋∠ECD＝∠BCD＋∠ECD＝45°， ∴∠PCE ＝∠BCD. 又∵PC DC ＝EC CB ，∴△PCE ∽△DCB ， ∴∠CBD ＝∠CEP＝90°， ∴∠ACB ＝∠CBD， ∴AC ∥BD ；(3)作PM ⊥BD ，交BD 的延长线于点M. ∵AC ＝42，△ABC 和△BEC 均为等腰直角三角形， ∴BE ＝CE ＝4. ∵△PCE ∽△DCB ， ∴EC CB ＝PE BD ，即442＝x BD， ∴BD ＝2x.∵∠PBM ＝∠CBD－∠CBP＝45°， BP ＝BE ＋PE ＝4＋x ， ∴PM ＝4＋x 2，∴S △PBD ＝12BD ·PM＝12×2x×4＋x 2 , ＝12x 2＋2x.。

第二节 锐角三角函数及解直角三角形的应用河北五年中考真题及模拟解直角三角形的应用1．(2017保定中考模拟)如图，已知△ABC 的三个顶点均在格点上，则cos A 的值为( D )A .33B .55C .233D .255(第1题图)(第2题图)2．(2017河北中考模拟)如图，Rt △ABC 中，∠BAC ＝90°，AD ⊥BC 于D ，若BD∶CD＝3∶2，则tan B ＝( D ) A .32 B .23 C .62 D .633．(2016河北中考模拟)在Rt △ABC 中，∠C ＝90°，如果cos B ＝12，那么sin A 的值是( B )A ．1B .12C .32 D .224．(2016定州中考模拟)如图，在Rt △ABC 中，∠C ＝90°，AB ＝13，BC ＝12.则下列三角函数表示正确的是( A )A ．sin A ＝1213B ．cos A ＝1213C ．tan A ＝512D ．tan B ＝1255．(2015河北中考)已知：岛P 位于岛Q 的正西方，由岛P ，Q 分别测得船R 位于南偏东30°和南偏西45°方向上，符合条件的示意图是( D ),A ) ,B ),C ) ,D )6．(2013河北中考)如图，一艘海轮位于灯塔P 的南偏东70°方向的M 处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P 的北偏东40°的N 处，则N 处与灯塔P 的距离为( D )A ．40海里B ．60海里C ．70海里D ．80海里(第6题图)(第7题图)7．(2016保定十三中二模)如图，港口A 在观测站O 的正东方向，OA ＝4.某船从港口A 出发，沿北偏东15°方向航行一段距离后到达B 处，此时从观测站O 处测得该船位于北偏东60°的方向，则该船航行的距离(即AB 的长)为．8张家口九中二模)芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁，大桥采用低塔斜拉桥桥型(如图①)，图②是从图①引伸出的平面图，假设你站在桥上测得拉索AB 与水平桥面的夹角是30°，拉索CD 与水平桥面的夹角是60°，两拉索顶端的距离BC 为2 m ，两拉索底端距离AD 为20 m ，请求出立柱BH 的长．(结果精确到0.1 m ，3≈1.732)解：设DH ＝x m .∵∠CDH ＝60°，∠H ＝90°，∴CH ＝DH·tan 60°＝3x ， ∴BH ＝BC ＋CH ＝2＋3x. ∵∠A ＝30°，∴AH ＝3BH ＝23＋3x. ∵AH ＝AD ＋D H ＝20＋x ， ∴23＋3x ＝20＋x ， 解得x ＝10－3，∴BH ＝2＋3(10－3)＝103－1≈16.3(m )． 答：立柱BH 的长约为16.3 m .9．(2016邯郸二十五中模拟)保护视力要求人写字时眼睛和笔端的距离应超过30 cm . 图①是一位同学的坐姿，把他的眼睛B ，肘关节C 和笔端A 的位置关系抽象成图②的△A BC. 已知BC ＝30 cm ，AC ＝22 cm ，∠ACB ＝53°，他的这种坐姿符合保护视力的要求吗？请说明理由. (参考数据：sin 53°≈0.8，cos 53°≈0.6，tan 53°≈1.3)解：他的这种坐姿不符合保护视力的要求． 理由：过点B 作BD⊥AC 于点D. ∵BC ＝30 cm ，∠ACB ＝53°，∴sin 53°＝BD BC ＝BD30≈0.8，解得：BD ＝24，cos 53°＝DCBC≈0.6，解得DC ＝18,∴AD ＝AC －DC ＝22－18＝4(cm )，∴AB ＝AD 2＋BD 2＝42＋242＝592<900， ∴他的这种坐姿不符合保护视力的要求．,中考考点清单)锐角三角函数的概念正弦 余弦 正切__特殊角的三角函数值三边关系两锐角关系边角关系解直角三角形的应用仰角、俯角(1)解直角三角形，当所求元素不在直角三角形中时，应作辅助线构造直角三角形，或寻找已知直角三角形中的边角替代所要求的元素；(2)解实际问题的关键是构造几何模型，大多数问题都需要添加适当的辅助线，将问题转化为直角三角形中的边角计算问题．,中考重难点突破)锐角三角函数及特殊角三角函数值【例1】(攀枝花中考)在△ABC 中，如果∠A，∠B 满足|tan A －1|＋⎝ ⎛⎭⎪⎫cos B －122＝0，那么∠C＝________. 【解析】先根据非负性，得tan A ＝1，cos B ＝12，求出∠A 及∠B 的度数，进而可得出结论．∵在△ABC 中，tan A ＝1，cos B ＝12，∴∠A ＝45°，∠B ＝60°，∴∠C ＝180°－∠A－∠B＝75°.【答案】75°1．在△ABC 中，若⎪⎪⎪⎪⎪⎪sin A －12＋⎝ ⎛⎭⎪⎫cos B －122＝0，则∠C 的度数是( D ) A ．30° B ．45° C ．60° D ．90°2．(2017天津中考)cos 60°的值等于( D )A . 3B ．1C .22 D .123．(2017日照中考)在Rt △ABC 中，∠C ＝90°，AB ＝13，AC ＝5，则sin A 的值为( B ) A .513 B .1213 C .512 D .1254．(孝感中考)式子2cos 30°－tan 45°－（1－tan 60°）2的值是( B ) A ．23－2 B ．0 C ．2 3 D ．2解直角三角形的实际应用【例2】(钦州中考)如图，在电线杆CD 上的C 处引拉线CE ，CF 固定电线杆，拉线CE 和地面所成的角∠CED ＝60°，在离电线杆6 m 的B 处安置高为1.5 m 的测角仪AB ，在A 处测得电线杆上C 处的仰角为30°，求拉线CE 的长．(结果保留小数点后一位，参考数据：2≈1.41，3≈1.73)【解析】由题意可先过点A 作AH⊥CD 于点H ，在Rt △ACH 中，可求出CH ，进而求出CD ＝CH ＋HD ＝CH ＋AB ，再在Rt △CED 中，求出CE 的长．【答案】解：过点A 作AH⊥CD，垂足为H ，由题意，可知四边形ABDH 为矩形，∠CAH ＝30°， ∴AB ＝DH ＝1.5，BD ＝AH ＝6.在Rt △ACH 中，tan ∠CAH ＝CHAH，∴CH ＝AH·tan ∠CAH ＝6tan 30°＝6×33＝23(m )．∵DH ＝1.5，∴CD ＝23＋1.5.在Rt △CDE 中，∠CED ＝60°，sin ∠CED ＝CDCE，∴CE ＝CDsin 60°＝4＋3≈5.7(m )，∴拉线CE 的长约为5.7 m .5．(2017兰州中考)如图，一个斜坡长130 m ，坡顶离水平地面的距离为50 m ，那么这个斜坡与水平地面夹角的正切值等于( C )A .513B .1213C .512D .1312(第5题图)(第6题图)6．(2016石家庄十一中二模)如图，某公园入口处原有三级台阶，每级台阶高为18 cm ，宽为30 cm ，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A ，斜坡的起始点为C ，现设计斜坡BC 的坡度i ＝1∶5，则AC 的长度是__210__cm .7．(2016保定十七中二模)如图，将45°的∠AOB 按下面的方式放置在一把刻度尺上：顶点O 与尺下沿的端点重合，OA 与尺下沿重合，OB 与尺上沿的交点B 在尺上的读数恰为2 cm .若按相同的方式将37°的∠AOC 放置在该刻度尺上，则OC 与尺上沿的交点C 在尺上的读数约为__2.7__cm .(结果精确到0.1 cm ，参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)8．(2016邢台中学二模)如图，在一笔直的海岸线l 上有A ，B 两个观测站，A 在B 的正东方向，AB ＝2 km .有一艘小船在点P 处，从A 处测得小船在北偏西60°的方向，从B 处测得小船在北偏东45°的方向．(1)求点P 到海岸线l 的距离；(2)小船从点P 处沿射线AP 的方向航行一段时间后，到达点C 处．此时，从B 处测得小船在北偏西15°的方向，求点C 与点B 之间的距离．(上述2小题的结果都保留根号)解：(1)过点P 作PD⊥AB 于点D. 设PD ＝x km .在Rt △P BD 中，∠BDP ＝90°，∠PBD ＝90°－45°＝45°， ∴BD ＝PD ＝x.在Rt △PAD 中，∠ADP ＝90°， ∠PAD ＝90°－60°＝30°， ∴AD ＝3PD ＝3x.∵BD ＋AD ＝AB ，∴x ＋3x ＝2，x ＝3－1. ∴点P 到海岸线l 的距离为(3－1)km ； (2)过点B 作BF⊥AC 于点F. 根据题意，得∠ABC＝105°.在Rt △ABF 中，∠AFB ＝90°，∠BAF ＝30°，∴BF ＝12AB ＝1.在△ABC中，∠C＝180°－∠BAC－∠ABC＝45°.在Rt△BCF中，∠BFC＝90°，∠C＝45°，∴BC＝2BF＝2，∴点C与点B之间的距离为 2 km.。

第五章 图形的相似与解直角三角形第一节 图形的相似与位似,遵义五年中考命题规律),遵义五年中考真题及模拟)相似三角形1．(2014遵义中考)如图，边长为2的正方形ABCD 中，P 是CD 的中点，连接AP 并延长交BC 的延长线于点F ，作△CPF 的外接圆⊙O，连接BP 并延长交⊙O 于点E ，连接EF ，则EF 的长为( D )A .32B .53C .35 5D .455,(第1题图)),(第2题图))2．(2017遵义十二中一模)如图，在平面直角坐标系中，以原点O 为位似中心，将△ABO 扩大到原来的2倍，得到△A′B′O.若点A 的坐标是(1，2)，则点A′的坐标是( C )A ．(2，4)B ．(－1，－2)C ．(－2，－4)D ．(－2，－1)3．(2014遵义中考)“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形ABCD ，东边城墙AB 长9里，南边城墙AD 长7里，东门点E ，南门点F 分别是AB ，AD的中点，EG ⊥AB ，FH ⊥AD ，EG ＝15里，HG 经过点A ，则FH ＝__1.05__ 里．4．(2017遵义中考)边长为22的正方形ABCD 中，P 是对角线AC 上的一个动点(点P 与A ，C 不重合)，连接BP ，将BP 绕点B 顺时针旋转90°到BQ ，连接QP ，QP 与BC 交于点E ，QP 的延长线与AD(或AD 延长线)交于点F.(1)连接CQ ，证明：CQ ＝AP ；(2)设AP ＝x ，CE ＝y ，试写出y 关于x 的函数关系式，并求当x 为何值时，CE ＝38BC ；(3)猜想PF 与EQ 的数量关系，并证明你的结论．解：(1)如图①，连接CQ.∵线段BP 绕点B 顺时针旋转90°得到线段BQ ， ∴BP ＝BQ ，∠PBQ ＝90°. ∵四边形ABCD 是正方形， ∴BA ＝BC ，∠ABC ＝90°， ∴∠ABC － ∠PBC＝∠PBQ－∠PBC， 即∠ABP＝∠CBQ.在△BAP 和△BCQ 中，⎩⎪⎨⎪⎧BA ＝BC ，∠ABP ＝∠CBQ，BP ＝BQ ，∴△BAP ≌△BCQ (SAS )， ∴CQ ＝AP ； (2)如图①，∵四边形ABCD 是正方形， ∴∠BAC ＝12∠BAD＝45°，∠BCA ＝12∠BCD＝45°，∴∠APB ＋∠ABP＝180°－45°＝135°. ∵DC ＝AD ＝22，由勾股定理得：AC ＝（22）2＋（22）2＝4. ∵AP ＝x ，∴PC ＝4－x.∵△PBQ 是等腰直角三角形， ∴∠BPQ ＝45°，∴∠APB ＋∠CPQ＝180°－45°＝135°， ∴∠CPQ ＝∠ABP. ∵∠BAC ＝∠ACB＝45°， ∴△APB ∽△CEP ， ∴AP CE ＝AB CP， ∴x y ＝224－x， ∴y ＝122x(4－x)＝－24x 2＋2x(0＜x ＜4)．∵CE ＝38BC ＝38×22＝324，∴y ＝－24x 2＋2x ＝324，解得x ＝3或1， ∴当x ＝3或1时，CE ＝38BC ；(3)PF ＝EQ.理由如下：如图②，当F 在边AD 上时，过P 作PG⊥FQ，交AB 于G ，则∠GPF＝90 °. ∵∠BPQ ＝45°， ∴∠GPB ＝45°. ∴∠GPB ＝∠PQB＝45°. ∵PB ＝BQ ，∠ABP ＝∠CBQ ， ∴△PGB ≌△QEB ， ∴EQ ＝PG. ∵∠BAD ＝90°， ∴F ，A ，G ，P 四点共圆． 连接FG ，∴∠FGP ＝∠FAP＝45°， ∴△FPG 是等腰直角三角形， ∴PF ＝PG ， ∴PF ＝EQ.当F 在AD 的延长线上时，如图③，同理可得： PF ＝PG ＝EQ.5．(2016遵义中考)如图，矩形ABCD 中，延长AB 至E ，延长CD 至F ，BE ＝DF ，连接EF ，与BC ，AD 分别相交于P ，Q 两点．(1)求证：CP ＝AQ ；(2)若BP ＝1，PQ ＝22，∠AEF ＝45°，求矩形ABCD 的面积． 解：(1)∵四边形ABCD 是矩形， ∴∠A ＝∠ABC＝∠C＝∠ADC＝90°， AB ＝CD ，AD ＝BC ，AB ∥BC ， ∴ ∠E ＝∠F.∵BE＝DF ，∴AE ＝CF. 在△CFP 和△AEQ 中，⎩⎪⎨⎪⎧∠C＝∠A，CF ＝AE ，∠F ＝∠E，∴△CFP ≌△AEQ(ASA )，∴CP ＝AQ ； (2)∵∠EBP＝∠FDQ＝90°， ∠F ＝∠AEF＝45°，∴△BEP ，△AEQ 是等腰直角三角形， ∴BE ＝BP ＝1，AQ ＝AE ，∴PE ＝2BP ＝2， ∴EQ ＝PE ＋PQ ＝2＋22＝32， ∴AQ ＝AE ＝3，∴AB ＝AE －BE ＝2. 由(1)知CP ＝AQ ， ∴CP ＝3，∴CB ＝CP ＋BP ＝1＋3＝4，∴矩形ABCD 的面积＝AB·BC＝2×4＝8.6．(2013遵义中考)如图，在Rt △ABC 中，∠C ＝90°，AC ＝4 cm ，BC ＝3 cm .动点M ，N 从点C 同时出发，均以每秒1 cm 的速度分别沿CA ，CB 向终点A ，B 移动，同时动点P 从点B 出发，以每秒2 cm 的速度沿BA 向终点A 移动，连接PM ，PN ，设移动时间为t.(单位：s ，0<t<2.5)(1)当t 为何值时，以A ，P ，M 为顶点的三角形与△ABC 相似？(2)是否存在某一时刻t ，使四边形APNC 的面积S 有最小值？若存在，求S 的最小值；若不存在，请说明理由．解：(1)在Rt △ABC 中，∵∠C ＝90°，AC ＝4 cm ，BC ＝3 cm ， ∴根据勾股定理，得AB ＝AC 2＋BC 2＝5 cm . 设AM ＝4－t ，则AP ＝5－2t ，BN ＝3－t.以A ，P ，M 为顶点的三角形与△ABC 相似，分两种情况： ①当△AMP∽△ABC 时，AP AC ＝AMAB ，即5－2t 4＝4－t 5，解得t ＝32； ②当△APM∽△ABC 时，AM AC ＝AP AB ，即4－t 4＝5－2t5，解得t ＝0(不合题意，舍去)． 综上所述，当t ＝32时，以A ，P ，M 为顶点的三角形与△ABC 相似；(2)存在．理由如下：过点P 作PH⊥BC 于点H ，则PH∥AC， ∴PH AC ＝BP BA ，即PH 4＝2t 5，∴PH ＝85t ， ∴S ＝S △ABC －S △BPN ＝12×3×4－12×(3－t)·85t＝45⎝ ⎛⎭⎪⎫t －322＋215(0<t<2.5)．∵45>0，∴S 有最小值， 当t ＝32时，S 最小值＝215.故当t ＝32时，四边形APNC 的面积S 有最小值，其最小值是215.,中考考点清单)比例的相关概念及性质1．线段的比：两条线段的比是两条线段的__长度__之比．2．比例中项：如果a b ＝b c ，即b 2＝__ac__，我们就把b 叫做a ，c 的比例中项．3．比例的性质：4.黄金分割：如图，如果点C 把线段AB 分成两条线段，使AC AB ＝__BCAC __，那么点C 叫做线段AC 的__黄金分割点__，AC 是BC 与AB 的比例中项，AC 与AB 的比叫做__黄金比__．相似三角形的判定及性质5．定义：对应角__相等__，对应边__成比例__的两个三角形叫做相似三角形，相似三角形对应边的比叫做相似比．6．性质(1)相似三角形的__对应角__相等；(2)相似三角形的对应线段(边、高、中线、角平分线)的比等于相似比； (3)相似三角形的周长比等于__相似比__，面积比等于__相似比的平方__． 7．判定(1)__两角__对应相等，两三角形相似；(2)两边对应成比例且__夹角__相等，两三角形相似； (3)三边__对应成比例__，两三角形相似；(4)两直角三角形的斜边和一条直角边__对应成比例__，两直角三角形相似． 【方法点拨】判定三角形相似的几条思路：(1)条件中若有平行线，可采用相似三角形的判定(1)．(2)条件中若有一对等角，可再找一对等角[用判定(1)]或再找夹边成比例[用判定(2)]． (3)条件中若有两边对应成比例，可找夹角相等．(4)条件中若有一对直角，可考虑再找一对等角或证明斜边、直角边对应成比例． (5)条件中若有等腰条件，可找顶角相等，可找一个底角相等，也可找底和腰对应成比例．【温馨提示】应注意相似三角形的对应边成比例，若已知△ABC∽△DEF，列比例关系式时，对应字母的位置一定要写正确，才能得到正确的答案．如：AB BC ＝DEEF，此式正确．那么想一想，哪种情况是错误的呢？请举例说明．相似多边形8．定义：对应角__相等__，对应边__成比例__的两个多边形叫做相似多边形，相似多边形对应边的比叫做它们的相似比．9．性质(1)相似多边形的对应边__成比例__； (2)相似多边形的对应角__相等__；(3)相似多边形周长的比__等于__相似比，相似多边形面积的比等于__相似比的平方__．位似图形10．定义：如果两个图形不仅是相似图形而且每组对应点所在的直线都经过同一个点，那么这样的两个图形叫做__位似图形__，这个点叫做__位似中心__，相似比叫做位似比．11．性质(1)在平面直角坐标系中，如果位似变换是以原点为中心，相似比为k ，那么位似图形对应点坐标的比等于__k 或－k__；(2)位似图形上任意一对对应点到位似中心的距离之比等于__位似比或相似比__．12．找位似中心的方法：将两个图形的各组对应点连接起来，若它们的直线或延长线相交于一点，则该点即是__位似中心__．13．画位似图形的步骤 (1)确定__位似中心__； (2)确定原图形的关键点；(3)确定__位似比__，即要将图形放大或缩小的倍数； (4)作出原图形中各关键点的对应点；(5)按原图形的连接顺序连接所作的各个对应点．,中考重难点突破)比例的性质【例1】已知a 5＝b 4＝c3，且3a －2b ＋c ＝20，则2a －4b ＋c 的值为________．【解析】设a 5＝b 4＝c3＝k(k≠0)，用含k 的式子表示a ，b ，c ，则a ＝5k ，b ＝4k ，c ＝3k ，代入等式3a －2b ＋c＝20求出k 值，再求出a ，b ，c 值代入可求．【答案】－61．(2016遵义六中一模)若y x ＝34，则x ＋yx 的值为( D )A ．1B .47C .54D .74相似三角形的判定与性质【例2】如图，M 为线段AB 的中点，AE 与BD 交于点C ，∠DME ＝∠A＝∠B＝α，且DM 交AC 于F ，ME 交BC 于G.(1)写出图中两对相似三角形并证明其中的一对；(2)请连接FG ，如果α＝45°，AB ＝42，AF ＝3，求FG 的长． 【解析】(1)两角对应相等的两个三角形是相似三角形；(2)由相似三角形性质求BG 长，由AB 长可求AC ，BC 长，在Rt △FCG 中由勾股定理求FG 长． 【答案】解：(1)△A MF∽△BGM ，△DMG ∽△DBM ，△EMF ∽△EAM(写出两对即可)． 证明△AMF∽△BGM 如下： ∵∠DME ＝∠A＝∠B＝α， ∴∠AMF ＋∠BMG＝180°－α. ∵∠A ＋∠AMF＋∠AFM＝180°， ∴∠AMF ＋∠AFM＝180°－α， ∴∠AFM ＝∠BMG，∴△AMF ∽△BGM ； (2)当α＝45°时，可得AC⊥BC，且AC ＝BC. ∵M 为AB 的中点，∴AM ＝BM ＝2 2. 又∵△AMF∽△BGM，∴AF AM ＝BMBG ，∴BG ＝AM·BM AF ＝22×223＝83.又AC ＝BC ＝42·cos 45°＝4， ∴CG ＝4－83＝43，CF ＝4－3＝1.在Rt △FCG 中，FG ＝CF 2＋CG 2＝12＋⎝ ⎛⎭⎪⎫432＝53.2．(2017庆阳二模)如图，在△ABC 中，D ，E 分别是AB ，AC 的中点，下列说法中不正确的是( D )A ．DE ＝12BC B .AD AB ＝AE ACC ．△ADE ∽△ABCD ．S △ADE ∶S △ABC ＝1∶23．(2017武威中考模拟)如图，在菱形ABCD 中，G 是BD 上一点，连接CG 并延长交BA 的延长线于点F ，交AD 于点E.求证：(1)AG ＝CG ； (2)AG 2＝GE·GF.证明：(1)∵四边形ABCD 是菱形， ∴AD ＝CD ，∠ADB ＝∠CDB， 在△ADG 与△CDG 中，⎩⎪⎨⎪⎧AD ＝CD ，∠ADG ＝∠CDG，DG ＝DG ，∴△ADG ≌△CDG ， ∴AG ＝CG ；(2)∵△ADG≌△CDG， ∴∠DAG ＝∠DCF. 又∵四边形ABCD 是菱形， ∴AB ∥CD ，∴∠F ＝∠DCF， ∴∠EAG ＝∠F.∵∠AGE ＝∠FGA，∴△AEG ∽△FAG ， ∴AG FG ＝EG AG，∴AG 2＝GE·GF.位似图形【例3】(2017遵义六中模拟)如图，在直角坐标系中，矩形OABC 的顶点O 在坐标原点，边OA 在x 轴上，OC 在y 轴上，如果矩形OA′B′C′与矩形OABC 关于点O 位似，且矩形OA′B′C′的面积等于矩形OABC 的面积的14，那么点B′的坐标是( ) A ．(－2，3) B ．(2，－3)C ．(3，－2)或(－2，3)D ．(－2，3)或(2，－3)【解析】根据面积比等于相似比的平方得到位似比为12，由图形得到点B 的坐标，根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标比等于tk ，即可得出答案．【答案】D4．(威海中考)如图，直线y ＝12x ＋1与x 轴交于点A ，与y 轴交于点B ，△BOC 与△B′O′C′是以点A 为位似中心的位似图形，且相似比为1∶3，则点B 的对应点B′的坐标为__(－8，－3)或(4，3)__．(第4题图)(第5题图)5．(2017云南中考)如图，D 是△ABC 的边BC 上一点，AB ＝4，AD ＝2，∠DAC ＝∠B.如果△ABD 的面积为15，那么△ACD 的面积为( D )A ．15B ．10C .152D ．5。

相似章节知识点总结数学在数学中，相似章节是一个重要的概念。

它涉及到图形之间的比较和相似性。

在这篇文章中，我们将讨论相似章节的定义、性质和一些相关的定理。

1. 相似章节的定义相似章节是指具有相同形状但不同大小的图形。

换句话说，如果两个图形的形状完全相同，但大小不同，那么它们就是相似的。

例如，如果有两个三角形，它们的对应角度相等，相应的边长成比例，那么这两个三角形就是相似的。

2. 相似章节的性质相似章节有一些重要的性质，包括：- 对应角相等：相似的图形之间的对应角是相等的。

这意味着如果两个图形是相似的，那么它们的对应角度是相等的。

- 对应边成比例：相似的图形之间的对应边是成比例的。

换句话说，如果两个图形是相似的，那么它们的对应边长之比是相等的。

3. 相似章节的定理相似章节有一些重要的定理，包括：- AAA相似定理：如果两个三角形的对应角度相等，则这两个三角形是相似的。

- AA相似定理：如果两个三角形的一个角相等，并且它们的一个对应边成比例，则这两个三角形是相似的。

- SAS相似定理：如果两个三角形的一条边成比例，并且它们的两个对应角度相等，则这两个三角形是相似的。

4. 相似章节的运用相似章节在实际问题中有许多应用，包括：- 遥感影像处理：在遥感影像处理中，相似章节用于计算不同尺度下的地物面积。

- 三角测量：在三角测量中，相似章节被用来计算不可达地点的距离和高度。

- 工程设计：在工程设计中，相似章节被用来设计结构物和道路等。

总之，相似章节是数学中一个重要的概念，它在几何学、工程和科学中都有着广泛的应用。

通过了解相似章节的定义、性质和定理，我们可以更好地理解和应用它们。

初中相似知识点总结一、相似三角形相似三角形是指具有对应角相等和对应边成比例的两个三角形。

当两个三角形中对应的角相等且对应的边成比例时，我们可以说这两个三角形是相似的。

相似三角形有以下几个重要的性质：1. AAA相似定理：如果两个三角形的对应角分别相等，那么这两个三角形是相似的。

2. AA相似定理：如果两个三角形的一对对应角相等，并且另一对角分别相等，那么这两个三角形是相似的。

3. SSS相似定理：如果两个三角形的对应边成比例，那么这两个三角形是相似的。

4. 相似三角形中，相似对应边的比例为任意一对相似边的比例。

相似三角形在几何学中有着重要的作用，在求解一些三角形的性质和问题时，我们经常需要利用相似三角形的性质进行推导和计算，因此学习相似三角形的性质对于初中的几何学知识是非常重要的。

二、相似多边形相似多边形是指具有对应角相等和对应边成比例的两个多边形。

相似多边形的性质和相似三角形相似，但在进行计算时需要更多的对应边的相似比例关系。

相似多边形有以下几个重要的性质：1. 如果两个多边形的对应角分别相等，且对应边成比例，那么这两个多边形是相似的。

2. 相似多边形中，任意一对相似边的比例都等于任意一个对应边的比例。

3. 相似多边形的面积比等于任意一对相似边的比例的平方。

相似多边形在几何学中也有着重要的作用，在计算多边形的面积、周长和其他性质时，相似多边形的性质能够为我们提供便利。

三、相似比相似比是指两个相似图形对应边的比例关系。

在相似三角形和相似多边形中，我们经常需要利用相似比来进行计算。

相似比的特点包括：1. 当两个相似三角形的对应边成比例时，这两个三角形的相似比就是对应边的比例关系。

2. 相似多边形的相似比与相似三角形相似比的性质类似，也是对应边的比例关系。

3. 在求解相似三角形和相似多边形的问题时，我们经常需要利用相似比进行计算和推导。

四、相似比的性质相似比有一些重要的性质，包括：1. 相似比的倒数：如果两个相似三角形的相似比为a：b，那么这两个三角形的相似比的倒数为b：a。