相似三角形之常用辅助线

三角形全等的判定+性质+辅助线技巧都在这里了，请收好！在初中三角形问题集中体现在“全等”和“相似”2大问题上，非常考验大家的解题能力、思维能力、耐性与定力。

有时证不出来，急不可耐、恨它恨的牙痒痒。

王老师这次整理了全等三角形判定、性质，最重要的是后面附上了所有证明全等三角形，包括添加各种辅助线的方法，认真看完这篇文章，保证关于三角形全等所有的题型你都会做！一、三角形全等的判定1.三组对应边分别相等的两个三角形全等(SSS)。

2.有两边及其夹角对应相等的两个三角形全等(SAS)。

3.有两角及其夹边对应相等的两个三角形全等(ASA)。

4.有两角及一角的对边对应相等的两个三角形全等(AAS)。

5.直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL)。

二、全等三角形的性质①全等三角形的对应边相等；全等三角形的对应角相等。

②全等三角形的周长、面积相等。

③全等三角形的对应边上的高对应相等。

④全等三角形的对应角的角平分线相等。

⑤全等三角形的对应边上的中线相等。

三、找全等三角形的方法(1)可以从结论出发，看要证明相等的两条线段（或角）分别在哪两个可能全等的三角形中；(2)可以从已知条件出发，看已知条件可以确定哪两个三角形相等；(3)从条件和结论综合考虑，看它们能一同确定哪两个三角形全等；(4)若上述方法均不行，可考虑添加辅助线，构造全等三角形。

三角形全等的证明中包含两个要素：边和角。

缺个角的条件：在初中三角形问题集中体现在“全等”和“相似”2大问题上，非常考验大家的解题能力、思维能力、耐性与定力。

有时证不出来，急不可耐、恨它恨的牙痒痒。

王老师这次整理了全等三角形判定、性质，最重要的是后面附上了所有证明全等三角形，包括添加各种辅助线的方法，认真看完这篇文章，保证关于三角形全等所有的题型你都会做！一、三角形全等的判定1.三组对应边分别相等的两个三角形全等(SSS)。

2.有两边及其夹角对应相等的两个三角形全等(SAS)。

一、相似的有关概念1．相似形具有相同形状的图形叫做相似形．相似形仅是形状相同，大小不一定相同．相似图形之间的互相变换称为相似变换． 2．相似图形的特性两个相似图形的对应边成比例，对应角相等． 3．相似比两个相似图形的对应角相等，对应边成比例．二、相似三角形的概念1．相似三角形的定义对应角相等，对应边成比例的三角形叫做相似三角形．如图，ABC △与A B C '''△相似，记作ABC A B C '''△∽△，符号∽读作“相似于”．A 'B 'C 'CB A2．相似比相似三角形对应边的比叫做相似比．全等三角形的相似比是1．“全等三角形”一定是“相似形”，“相似形”不一定是“全等形”．三、相似三角形的性质1．相似三角形的对应角相等如图，ABC △与A B C '''△相似，则有A A B B C C '''∠=∠∠=∠∠=∠，，．A 'B 'C 'CB A2．相似三角形的对应边成比例 如图，ABC △与A B C '''△相似，则有AB BC AC kA B B C A C ===''''''（k 为相似比）．相似三角形的性质及判定A 'B 'C 'CB A3．相似三角形的对应边上的中线，高线和对应角的平分线成比例，都等于相似比．如图1，ABC △与A B C '''△相似，AM 是ABC △中BC 边上的中线，A M ''是A B C '''△中B C ''边上的中线，则有AB BC AC AM k A B B C A C A M ====''''''''（k 为相似比）．M 'MA 'B 'C 'C BA图1如图2，ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AH k A B B C A C A H ====''''''''（k 为相似比）．H 'H AB C C 'B 'A '图2如图3，ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC AD k A B B C A C A D ====''''''''（k 为相似比）．D 'D A 'B 'C B A图34．相似三角形周长的比等于相似比． 如图4，ABC △与A B C '''△相似，则有AB BC AC k A B B C A C ===''''''（k为相似比）．应用比例的等比性质有AB BC AC AB BC AC kA B B C A C A B B C A C ++====''''''''''''++．A 'B 'C 'CB A图45．相似三角形面积的比等于相似比的平方．如图5，ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AH k A B B C A C A H ====''''''''（k 为相似比）．进而可得21212ABC A B C BC AHS BCAHkS B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．H 'H AB C C 'B 'A '图5四、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似．五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有“三点定形法”． 1．横向定型法 欲证AB BC BEBF=，横向观察，比例式中的分子的两条线段是AB 和BC ，三个字母A B C ，，恰为ABC △的顶点；分母的两条线段是BE 和BF ，三个字母B E F ，，恰为BEF △的三个顶点．因此只需证ABC EBF△∽△．2．纵向定型法欲证AB D E BCEF=，纵向观察，比例式左边的比AB 和BC 中的三个字母A B C ，，恰为ABC △的顶点；右边的比两条线段是D E 和EF 中的三个字母D E F ，，恰为D E F △的三个顶点．因此只需证ABC D EF△∽△．3．中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况，此时可考虑运用等线，等比或等积进行变换后，再考虑运用三点定形法寻找相似三角形．这种方法就是等量代换法．在证明比例式时，常用到中间比．比例中项式的证明，通常涉及到与公共边有关的相似问题。

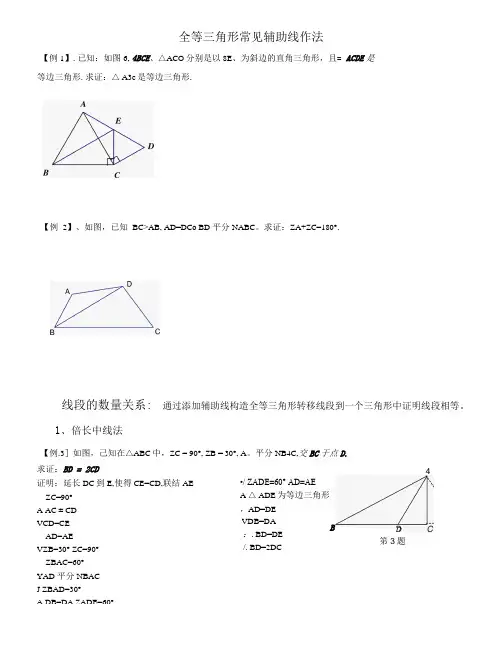
全等三角形常见辅助线作法【例1】.已知：如图6, 4BCE、△ACO分别是以8E、为斜边的直角三角形，且= ACDE是等边三角形.求证：△ A3c是等边三角形.【例2】、如图，已知BC>AB, AD=DCo BD 平分NABC。

求证：ZA+ZC=180°.线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。

1、倍长中线法【例.3］如图，己知在△ABC中，ZC = 90°, ZB = 30°, A。

平分NB4C,交BC于点D.求证：BD = 2CD证明：延长DC到E,使得CE=CD,联结AEZC=90°A AC ± CDVCD=CEAD=AEVZB=30° ZC=90°ZBAC=60°YAD 平分NBACJ ZBAD=30°A DB=DA ZADE=60°VDB=DA：.BD=DE/. BD=2DC4B D笫3题•/ ZADE=60° AD=AEA △ ADE为等边三角形，AD=DE【例4.】如图，。

是AABC的边上的点，且CD = AB, ZADB = ZBAD, AE是AARD的中线。

求证：AC = 2AEo 证明：延长AE至IJ点F,使得EF=AE联结DF在4ABE和4FDE中BE=DEZAEB=ZFEDAE=FE/.△ABE 也AFDE (SAS) A AB=FD ZABE=ZFDE VAB=DCJ FD = DCZADC=ZABD+ZBAD ZADB = ZBAD，ZADC=ZABD+ZBDA VZABE=ZFDE・・・NADONADB+NFDE即ZADC= ZADF ffiAADF 和AADC 中AD=AD< ZADF= ZADC、DF =DC・•・△ ADF也ADC(SAS) AAF=ACAC=2AE【变式练习】、如图，AABC中，BD二DOAC, E是DC的中点，求证：AD平分NBAE.【小结】熟悉法一、法三“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法, 倍长中线，或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。

类似三角形添加帮助线的办法举例例1： 已知：如图,△ABC 中,AB ＝AC,BD ⊥AC 于D ． 求证： BC 2＝2CD ·AC ．例2上的一点,（1;（2值例3．如图4-1,已知平行四边ABCD 中,E 是AB 的中点连E.F 交AC 于G ．求AG ：AC 的值．例4.如图4—5,B 为AC 的中点,E 为BD 的中点,则AF ：AE=___________. 例5.如图4-7,已知平行四边形ABCD 中,对角线AC.BD 交于O 点,E 为AB 延伸线上一点,OE 交BC 于F,若AB=a,BC=b,BE=c,求BF 的长． 例6.已知在△ABC 中,AD 是∠BAC类似三角形添加帮助线的办法举例答案例1： 已知：如图,△ABC 中,AB ＝AC,BD ⊥AC 于D ． 求证： BC 2＝2CD ·AC ． 剖析：欲证BC 2＝2CD ·AC,论中有“2”,无法直接找到它们地点的类似三角形,是以须要联合图形特色及结论情势,经由过程添加帮助线,对个中某一线段进行倍.分变形,结构出单一线段后,再证实三角形类似．由“2”所放的地位不合,证法也不合．BCBC证法一（结构2CD ）：如图,在AC 截取DE ＝DC, ∵BD ⊥AC 于D,∴BD 是线段CE 的垂直等分线, ∴BC=BE,∴∠C=∠BEC, 又∵ AB ＝AC, ∴∠C=∠ABC ． ∴△BCE ∽△ACB ．∴BC 2＝2CD ·AC ．证法二（结构2AC ）：如图,在CA 的延伸线上截取AE ＝AC,贯穿连接BE,∵ AB ＝AC, ∴ AB ＝AC=AE ． ∴∠EBC=90°, 又∵BD ⊥AC ．∴∠EBC=∠BDC=∠EDB=90°, ∴∠E=∠DBC, ∴△EBC ∽△BDC∴BC 2＝2CD ·AC．证法三,取BC 的中点E,贯穿连接BCEBCAE,则又∵AB=AC,∴AE ⊥BC,∠ACE=∠C ∴∠AEC=∠BDC=90° ∴△ACE ∽△BCD ．∴BC 2＝2CD ·AC ．证法四,取BC 中点E,贯穿连接DE,．∵BD ⊥AC,∴BE=EC=EB, ∴∠EDC=∠C又∵AB=AC,∴∠ABC=∠C, ∴△ABC ∽△EDC ．∴BC 2＝2CD ·AC ．解释：此题充分展现了添加帮助线,结构类似形的办法和技能．在解题中办法要灵巧,思绪要坦荡．例2,贯穿连接（1;（2B值（1解法1如图,解法2如图同解法1解法3如图以下同解法1解法4如图,且,解法5如图得平行四边形,,解法6如图（补形法）,,（注：此外可用三角形类似.等腰三角形三线合和一.等积法等）（2解法1（补形法）如图解法2（补形法）如图,解法3（补形法）如图1）2）由（1）.（2解法4（割补法）如图如图,解释本题分解考核了等腰三角形的性质,类似三角形的剖断和性质,解题症结是作帮助线,结构类似三角形.例3．如图4-1,已知平行四边ABCD中,E是AB的中点连E.F交AC于G．求AG：AC的值．解法1：延伸FE交CB的延伸线于H,∵四边形ABCD是平行四边形,∴∠H=∠AFE,∠DAB=∠HBE又AE=EB,∴△AEF≌△BEH,即AF=BH,∵ AD∥CH,∠AGF=∠CGH,∠AFG=∠BHE,∴△AFG∽△CGH．∴ AG：GC=AF：CH,∴ AG：GC=1：4,∴ AG：AC=1：5．解法2：如图4—2,延伸EF与CD的延伸线交于M,由平行四边形ABCD可知即AB∥MC,∴ AF：FD=AE：MD,AG：GC=AE：MC．∴ AF：FD=1：2,∴ AE：MD=1：2．AE：MC=1：4,即AG：GC=1：4,∴ AG：AC=1：5例4.如图4—5,B为AC的中点,E为BD的中点,则AF：AE=___________.解析：取CF的中点G,衔接BG．∵ B为AC的中点,∴ BG：AF=1：2,且BG∥AF,又E为BD的中点,∴ F为DG的中点．∴ EF：BG=1：2．故EF：AF=1：4,∴ AF：AE=4：3．例5.如图4-7,已知平行四边形ABCD中,对角线AC.BD交于O点,E为AB延伸线上一点,OE交BC于F,若AB=a,BC=b,BE=c,求BF的长．解法1：过O点作OM∥CB交AB于M,∵ O是AC中点,OM∥CB,∴ M是AB的中点,∴ OM是△ABC的中位线且OM∥BC,∠EFB=∠EOM,∠EBF=∠EMO．∴△BEF∽△MOE,解法2：如图4-8,延伸EO与AD交于点G,则可得△AOG≌△COF,∴ AG=FC=b-BF,∵ BF∥AG,解法3：延伸EO与CD的延伸线订交于N,则△BEF与△CNF的对应边成比例,例6.已知在△ABC中,AD是∠BAC剖析 1 比例线段常由平行线而产生,因而研讨比例线段问题,常应留意平行线的感化,在没有平行线时,可以添加平行线而促成比例线段的产生．此题中AD为△ABC内角A的等分线,这里不消失平行线,于是可斟酌过定点作某定直线的平行线,添加了如许的帮助线后,就可以应用平行关系找出响应的比例线段,再比较所证的比例式与这个比例式的关系,去寻找问题的解决．证法1：如图4—9,过C点作CE∥AD,交BA的延伸线于E．在△BCE中,∵ DA∥CE,又∵ CE∥AD,∴∠1=∠3,∠2=∠4,且AD等分∠BAC,∵∠1=∠2,于是∠3=∠4,∴ AC=AE剖析2 因为BD.CD是点D分BC而得,故可过火点D作平行线．证法2：如图4—10,过D作DE∥AC交AB于E,则∠2=∠3．∵∠1=∠2,∴∠1=∠3．于是EA=ED．剖析3 欲证式子左边为AB：AC,而AB.AC不在统一向线上,又不服行,故斟酌将AB转移到与AC平行的地位．证法3：如图4—11,过B作BE∥AC,交AD的延伸线于E,则∠2=∠E．∵∠1=∠2,∴∠1=∠E,AB=BE．剖析4 因为AD是∠BAC的等分线,故可过D分离作AB.AC的平行线,结构类似三角形求证．证法4 如图4—12,过D点作DE∥AC交AB于E,DF∥AB交AC于F．易证四边形AEDF是菱形．则 DE=DF．由△BDE∽△DFC,。

一、相似的有关概念1．相似形具有相同形状的图形叫做相似形．相似形仅是形状相同，大小不一定相同．相似图形之间的互相变换称为相似变换． 2．相似图形的特性两个相似图形的对应边成比例，对应角相等． 3．相似比两个相似图形的对应角相等，对应边成比例．二、相似三角形的概念1．相似三角形的定义对应角相等，对应边成比例的三角形叫做相似三角形．如图，ABC △与A B C '''△相似，记作ABC A B C '''△∽△，符号∽读作“相似于”．A 'B 'C 'CB A2．相似比相似三角形对应边的比叫做相似比．全等三角形的相似比是1．“全等三角形”一定是“相似形”，“相似形”不一定是“全等形”．三、相似三角形的性质1．相似三角形的对应角相等如图，ABC △与A B C '''△相似，则有A A B B C C '''∠=∠∠=∠∠=∠，，．A 'B 'C 'CB A2．相似三角形的对应边成比例 如图，ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）． 相似三角形的性质及判定A 'B 'C 'CB A3．相似三角形的对应边上的中线，高线和对应角的平分线成比例，都等于相似比．如图1，ABC △与A B C '''△相似，AM 是ABC △中BC 边上的中线，A M ''是A B C '''△中B C ''边上的中线，则有AB BC AC AMk A B B C A C A M ====''''''''（k 为相似比）． M 'MA 'B 'C 'C BA图1如图2，ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AHk A B B C A C A H ====''''''''（k 为相似比）． H 'H AB C C 'B 'A '图2如图3，ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC ADk A B B C A C A D ====''''''''（k 为相似比）．D 'D A 'B C 'C B A图34．相似三角形周长的比等于相似比． 如图4，ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++．A 'B 'C 'CB A图45．相似三角形面积的比等于相似比的平方．如图5，ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AHk A B B C A C A H ====''''''''（k 为相似比）．进而可得21212ABC A B C BC AH S BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．H 'H AB C C 'B 'A '图5四、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似．五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有“三点定形法”． 1．横向定型法欲证AB BCBE BF=，横向观察，比例式中的分子的两条线段是AB 和BC ，三个字母A B C ，，恰为ABC △的顶点；分母的两条线段是BE 和BF ，三个字母B E F ，，恰为BEF △的三个顶点．因此只需证2．纵向定型法欲证AB DEBC EF=，纵向观察，比例式左边的比AB 和BC 中的三个字母A B C ，，恰为ABC △的顶点；右边的比两条线段是DE 和EF 中的三个字母D E F ，，恰为D E F △的三个顶点．因此只需证ABC DEF △∽△． 3．中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况，此时可考虑运用等线，等比或等积进行变换后，再考虑运用三点定形法寻找相似三角形．这种方法就是等量代换法．在证明比例式时，常用到中间比．比例中项式的证明，通常涉及到与公共边有关的相似问题。

构造相似辅助线（1）——双垂直模型6.在平面直角坐标系xOy中，点A的坐标为(2，1)，正比例函数y=kx 的图象与线段OA的夹角是45°，求这个正比例函数的表达式．7.在△ABC中，AB=，AC=4，BC=2，以AB为边在C点的异侧作△ABD，使△ABD为等腰直角三角形，求线段CD的长．8.在△ABC中，AC=BC，∠ACB=90°，点M是AC上的一点，点N是BC上的一点，沿着直线MN折叠，使得点C恰好落在边AB上的P点．求证：MC：NC=AP：PB．9.如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y 轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折B点落在D 点的位置，且AD交y轴于点E．那么D点的坐标为（）A. B.C. D.10..已知，如图，直线y=﹣2x＋2与坐标轴交于A、B两点．以AB为短边在第一象限做一个矩形ABCD，使得矩形的两边之比为1﹕2。

求C、D两点的坐标。

6.答案：解：分两种情况第一种情况，图象经过第一、三象限过点A作AB⊥OA，交待求直线于点B，过点A作平行于y轴的直线交x轴于点C，过点B作BD⊥AC 则由上可知：＝90°由双垂直模型知：△OCA∽△ADB ∴∵A（2，1），＝45°∴OC＝2，AC＝1，AO＝AB∴AD＝OC＝2，BD＝AC＝1∴D点坐标为（2，3）∴B点坐标为（1，3）∴此时正比例函数表达式为：y＝3x第二种情况，图象经过第二、四象限过点A作AB⊥OA，交待求直线于点B，过点A作平行于x轴的直线交y轴于点C，过点B作BD⊥AC 则由上可知：＝90°由双垂直模型知：△OCA∽△ADB ∴∵A（2，1），＝45°∴OC＝1，AC＝2，AO＝AB ∴AD＝OC＝1，BD＝AC＝2∴D点坐标为（3，1）∴B点坐标为（3，﹣1）∴此时正比例函数表达式为：y＝x7.答案：解：情形一：情形二：情形三：8.答案：证明：方法一：连接PC，过点P作PD⊥AC于D，则PD//BC根据折叠可知MN⊥CP ∵∠2+∠PCN=90°，∠PCN+∠CNM=90°∴∠2=∠CNM ∵∠CDP=∠NCM=90°∴△PDC∽MCN∴MC：CN=PD：DC ∵PD=DA ∴MC：CN=DA：DC∵PD//BC ∴DA：DC=PA：PB ∴MC：CN=PA：PB方法二：如图，过M作MD⊥AB于D，过N作NE⊥AB于E由双垂直模型，可以推知△PMD∽NPE，则，根据等比性质可知，而MD=DA，NE=EB，PM=CM，PN=CN，∴MC：CN=PA：PB9.答案：A解题思路：如图过点D作AB的平行线交BC的延长线于点M，交x轴于点N，则∠M=∠DNA=90°，由于折叠，可以得到△ABC≌△ADC，又由B（1，3）∴BC=DC=1，AB=AD=MN=3，∠CDA=∠B=90°∴∠1+∠2=90°∵∠DNA=90°∴∠3+∠2=90°∴∠1=∠3∴△DMC∽△AND，∴设CM=x，则DN=3x，AN=1＋x，DM＝∴3x＋＝3 ∴x＝∴，则。

初中数学常用辅助线大全初中数学中，辅助线是解决几何问题的重要工具。

通过添加适当的辅助线，可以转化问题，使其更容易解决。

以下是初中数学中常用的辅助线做法：1. 中点连接线：如果一条线段被另一条线段平分，则可以作出中点连接线。

中点连接线将原图形分为面积相等、形状相同的两部分。

2. 平行线：通过作平行线，可以将复杂的几何图形转化为简单的、易于处理的图形。

平行线有助于证明角度相等、线段相等和全等三角形。

3. 延长线：在需要证明某一直线或线段等于另一条直线或线段时，可以通过延长线的方式将问题简化。

4. 垂线：在证明角相等、三角形全等或线段长度等问题时，经常需要作垂线。

垂足将线段分为两段相等的部分，有助于证明和计算。

5. 角平分线：角平分线将角分为两个相等的部分，有助于证明角度相等和线段长度相等。

6. 构造法：在某些情况下，需要通过构造新的图形来解决问题。

例如，构造一个与原图形相似的三角形或平行四边形。

7. 截长补短法：当需要证明某一直线或线段等于两条其他直线或线段的和时，可以通过截长或补短的方式来证明。

8. 辅助圆：在证明与圆相关的问题时，有时需要作辅助圆。

通过辅助圆，可以将问题转化为与圆相关的定理和性质。

除了以上常用方法外，还有一些特殊图形的辅助线做法。

例如，在等腰三角形中，可以通过作底边上的高或中线来证明性质；在直角三角形中，可以通过作斜边上的中线来证明性质。

为了更好地掌握辅助线的做法，学生需要多做练习题，积累经验并熟悉各种题型。

同时，要注意总结和归纳，发现不同问题之间的联系和规律，以便能够更快地找到解决问题的方法。

另外，值得注意的是，辅助线并不是随意添加的，需要遵循一定的逻辑和推理。

添加的辅助线必须与原图形有清晰的关系，不能凭空创造。

同时，要注意证明过程中每一步的逻辑严密性，确保证明过程是正确的。

综上所述，初中数学中的辅助线做法是解决几何问题的关键。

通过熟练掌握各种辅助线的做法，学生可以更好地解决复杂的几何问题，提高数学成绩。

几何常见辅助线口诀三角形图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

线段和差及倍半，延长缩短可试验。

线段和差不等式，移到同一三角去。

三角形中两中点，连接则成中位线。

三角形中有中线，倍长中线得全等。

四边形平行四边形出现，对称中心等分点。

梯形问题巧转换，变为三角或平四。

平移腰，移对角，两腰延长作出高。

如果出现腰中点，细心连上中位线。

上述方法不奏效，过腰中点全等造。

证相似，比线段，添线平行成习惯。

等积式子比例换，寻找线段很关键。

直接证明有困难，等量代换少麻烦。

斜边上面作高线，比例中项一大片。

圆形半径与弦长计算，弦心距来中间站。

圆上若有一切线，切点圆心半径联。

切线长度的计算，勾股定理最方便。

要想证明是切线，半径垂线仔细辨。

是直径，成半圆，想成直角径连弦。

弧有中点圆心连，垂径定理要记全。

圆周角边两条弦，直径和弦端点连。

弦切角边切线弦，同弧对角等找完。

要想作个外接圆，各边作出中垂线。

还要作个内接圆，内角平分线梦圆。

如果遇到相交圆，不要忘作公共弦。

内外相切的两圆，经过切点公切线。

若是添上连心线，切点肯定在上面。

要作等角添个圆，证明题目少困难。

由角平分线想到的辅助线一、截取构全等如图，AB//CD，BE平分∠ABC，CE平分∠BCD，点E在AD上，求证：BC=AB+CD。

分析：在此题中可在长线段BC上截取BF=AB，再证明CF=CD，从而达到证明的目的。

这里面用到了角平分线来构造全等三角形。

另外一个全等自已证明。

此题的证明也可以延长BE与CD的延长线交于一点来证明。

自已试一试。

二、角分线上点向两边作垂线构全等如图，已知AB>AD, ∠BAC=∠FAC,CD=BC。

求证：∠ADC+∠B=180分析：可由C向∠BAD的两边作垂线。

近而证∠ADC与∠B之和为平角。

三、三线合一构造等腰三角形如图，AB=AC，∠BAC=90 ，AD为∠ABC的平分线，CE⊥BE.求证：BD=2CE。

全等三角形的辅助线的常见添法一、前言全等三角形是初中数学中一个重要的概念，其性质和应用十分广泛。

在解决全等三角形相关问题时，辅助线的运用是非常常见的方法之一。

本文将介绍几种常见的全等三角形辅助线添法。

二、中线中线是连接三角形一个顶点和对边中点的线段。

在全等三角形的证明中，经常使用到中线。

1. 作平移假设有两个全等三角形ABC和DEF，需要证明它们完全重合。

可以在BC上取一点M，在EF上取一点N，连接MN，并作平移使得BC重合于EF，即可证明ABC和DEF完全重合。

2. 作垂线假设有两个全等三角形ABC和DEF，需要证明它们完全重合。

可以在BC上取一点M，在EF上作MN垂直于EF，并延长至交于P，则BP=FP，CP=EP，因此可以通过SAS（边-角-边）准则证明ABC和DEF完全重合。

三、高线高线是从一个顶点向对边所在直线作垂线所得到的线段。

在证明两个直角三角形相似时常用到高线。

1. 作垂心假设有两个直角三角形ABC和DEF，需要证明它们相似。

可以在ABC 中作垂心H，连接AH、BH、CH，并在DEF中作DH垂直于EF，延长至交于K，则AK=DK，因此可以通过AA（角-角）准则证明ABC 和DEF相似。

2. 作中线假设有两个三角形ABC和DEF，其中BC=EF，需要证明它们相似。

可以在BC上取一点M，在EF上取一点N，连接MN，并作垂线PH 垂直于MN且交于O，则PO为MN的中线。

由于BM=FN，BO=EO（因为PH平分MN），因此可以通过SAS准则证明ABC和DEF相似。

四、角平分线角平分线是从一个顶点出发将角分成两个相等的角所得到的线段。

在证明两个三角形相似时常用到角平分线。

1. 作等腰三角形假设有两个三角形ABC和DEF，其中∠BAC=∠EDF且AC=DF，需要证明它们相似。

可以在BC上取一点M，在EF上取一点N，并连接AN、BM以及CN与AM的交点为P，则AP=PN（因为AP是∠BAC 的平分线），BP=PM（因为BP是∠ABM的平分线），因此可以通过SAS准则证明ABC和DEF相似。

相似证明方法在数学和科学研究中，证明两个对象或现象相似的方法是非常重要的。

相似性的证明可以帮助我们理解事物之间的关联，推断出新的结论，甚至指导我们解决实际问题。

本文将介绍几种常见的相似证明方法，帮助读者更好地理解和运用相似性的概念。

一、比例法。

比例法是证明两个对象或现象相似的常用方法之一。

当我们需要证明两个图形相似时，可以通过比较它们对应边的比例来进行证明。

例如，对于两个三角形ABC和DEF，如果它们的对应边长之比相等，即AB/DE=BC/EF=AC/DF，那么可以得出这两个三角形是相似的。

比例法的优点是简单直观，容易理解和应用，适用于各种类型的图形。

二、角度法。

角度法是另一种常见的相似证明方法。

在证明两个三角形相似时，我们可以通过比较它们的对应角度来进行证明。

如果两个三角形的对应角相等，即角A等于角D，角B等于角E，角C等于角F，那么可以得出这两个三角形是相似的。

角度法的优点是适用范围广，不仅适用于三角形，也适用于其他类型的图形。

三、辅助线法。

辅助线法是在证明图形相似时常用的方法之一。

通过引入辅助线，我们可以将原来的图形分解成若干个简单的几何图形，从而更容易进行相似性的证明。

例如，在证明两个三角形相似时，我们可以通过引入垂直平分线、中位线等辅助线，将原来的三角形分解成若干个全等的三角形，从而得出它们是相似的结论。

辅助线法的优点是能够简化证明过程，使证明更直观、更易理解。

四、比较法。

比较法是在证明两个对象或现象相似时常用的方法之一。

通过比较它们的性质、特征、规律等，我们可以得出它们之间的相似性。

例如，在证明两个函数相似时，我们可以比较它们的定义域、值域、增减性、奇偶性等性质，从而得出它们是相似的结论。

比较法的优点是灵活多样，适用于各种类型的对象或现象。

五、数学归纳法。

数学归纳法是在证明一类对象或现象相似时常用的方法之一。

通过证明某个基本情况成立，并假设对于任意n都成立，然后证明n+1也成立，从而得出结论。

相似三角形的性质(经典全面)相似三角形的性质及判定一、相似的有关概念相似形是指具有相同形状的图形，但大小不一定相同。

相似图形之间的互相变换称为相似变换。

二、相似三角形的概念相似三角形是指对应角相等，对应边成比例的三角形。

用符号XXX表示，例如△ABC∽△A B C。

三、相似三角形的性质1.对应角相等：如果△ABC与△A B C相似，则有A A，B B，C C。

2.对应边成比例：如果△ABC与△A B C相似，则有AB/BC=AC/A C=BC/B C=k（k为相似比）。

3.对应边上的中线、高线和对应角的平分线成比例，都等于相似比。

例如，如果AM是△ABC中BC边上的中线，A M是△A B C中B C边上的中线，则有AM/A M=k。

如果AH是△ABC中BC边上的高线，A H是△A B C中B C边上的高线，则有AH/A H=k。

如果AD是△ABC中BAC的角平分线，A D是△A B C中B A C的角平分线，则有AD/A D=k。

4.相似三角形周长的比等于相似比。

如果△ABC与△A B C相似，则有AB+BC+AC/A B+B C+A C=k。

ABCD中间观察，比例式中的比AD和BC中的三个字母A，B，C恰为△ABC的顶点；比CD和EF中的三个EFDC字母D，E，F恰为△DEF的三个顶点．因此只需证欲证△ABC∽△DEF．证明比例中项式或倒数式或复合式的方法，可以运用“三点定形法”，也可以利用“分离比例中项法”或“分离倒数式法”或“分离复合式法”．由于在运用三点定形法时，可能会遇到三点共线或四点中没有相同点的情况，此时可以考虑使用等线、等比或等积进行变换，然后再使用三点定形法来寻找相似三角形。

这种方法被称为等量代换法。

在证明比例式时，常常会用到中间比。

证明比例中项式通常涉及与公共边有关的相似问题。

这类问题的典型模型是射影定理模型，需要熟练掌握和透彻理解其特征和结论。

证明倒数式往往需要先进行变形，将等式的一边化为1，另一边化为几个比值的形式，然后对比值进行等量代换，进而证明之。

专训2 巧作平行线构造相似三角形 名师点金：解题时，往往会遇到要证的问题与相似三角形联系不上或者说图中根本不存在相似三角形的情况，添加辅助线构造相似三角形是这类几何证明题的一种重要方法．常作的辅助线有以下几种：(1)由比例式作平行线；(2)有中点时，作中位线；(3)根据比例式，构造相似三角形．巧连线段的中点构造相似三角形1．如图，在△ABC 中，E ，F 是边BC 上的两个三等分点，D 是AC 的中点，BD 分别交AE ，AF 于点P ，Q ，求BP PQ QD.(第1题)过顶点作平行线构造相似三角形2．如图，在△ABC 中，AC ＝BC ，F 为底边AB 上一点，BFAF ＝32，取CF 的中点D ，连接AD 并延长交BC 于点E ，求BE EC 的值．(第2题)过一边上的点作平行线构造相似三角形3．如图，在△ABC 中，AB ＞AC ，在边AB 上取一点D ，在AC 上取一点E ，使AD ＝AE ，直线DE 和BC 的延长线交于点P.求证：BP CP ＝BD EC.(第3题)过一点作平行线构造相似三角形4．如图，在△ABC 中，点M 为AC 边的中点，点E 为AB 上一点，且AE ＝14AB ，连接EM 并延长交BC 的延长线于点D.求证：BC ＝2CD.(第4题)答案1．解：如图，连接DF ，∵E，F 是边BC 上的两个三等分点，∴BE＝EF ＝FC.∵D 是AC 的中点，∴AD＝CD.∴DF 是△ACE 的中位线．∴DF∥AE，且DF ＝12AE.∴DF∥PE. ∴△BEP∽△BFD.∴BE BF ＝PE DF ＝BP BD. ∵BF＝2BE ，∴DF＝2PE ，BD ＝2BP.∴BP＝PD.∵DF∥AE，∴△APQ∽△FDQ.∴PQ QD ＝AP DF. 设PE ＝a ，则DF ＝2a ，AP ＝3a.∴PQ QD ＝AP DF ＝32. ∴BP PQ QD ＝53 2.(第1题) (第2题)2．解：如图，过点C 作C G∥AB 交AE 的延长线于点G.∴△GCD∽△AFD.∴CG FA ＝CD FD. 又∵D 为CF 的中点，∴CD ＝FD.∴AF＝CG.∵BF AF ＝32，∴AB AF ＝5 2.∵AB∥CG，∴△ABE∽△GCE.∴BE EC ＝AB CG ＝AB AF ＝52. 3．证明：如图，过点C 作CF∥AB 交DP 于点F ，∴△PCF∽△PBD.∴BP CP ＝BD CF. ∵AD∥CF，∴∠ADE＝∠EFC.(第3题)∵AD＝AE ，∴∠ADE＝∠AED.∵∠AED ＝∠CEP，∴∠EFC＝∠CE P.∴EC＝CF.∴BP CP ＝BD EC.4．证明：(方法一)如图①，过点C 作CF∥AB，交DE 于点F ，(第4题①) ∴△CDF∽△BDE.∴CF BE ＝CD BD . ∵点M 为AC 边的中点， ∴AM＝CM. 易证△AME≌△CMF.∴AE＝C F.∵AE＝14AB ，∴BE＝3AE. ∴AE BE ＝13.∵CF BE ＝CD BD ， ∴AE BE ＝CD BD ＝13，即BD ＝3CD.∴BC ＝2CD.(第4题②)(方法二)如图②，过点C 作CF∥DE，交AB 于点F ，∴AE AF ＝AM AC. 又∵点M 为AC 边的中点，∴AC＝2AM.∴2AE＝AF.∴AE＝EF.又∵AE AB ＝14，∴BF EF＝2. 又∵CF∥DE，∴BF FE ＝BC CD＝2. ∴BC＝2CD.(第4题③)(方法三)如图③，过点E 作EF∥BC，交AC 于点F ，∴△AEF∽△ABC.∴EF BC ＝AE AB ＝AF AC.由AE ＝14AB ，知EF BC ＝AF AC ＝AE AB ＝14， ∴EF＝14BC ，AF ＝14AC. 由E F∥CD，得△EFM∽△DCM，∴EF CD ＝MF MC .又∵AM＝MC ，∴MF＝12MC. ∴EF＝12CD.∴BC＝2CD.(第4题④)(方法四)如图④，过点A 作AF∥BD，交DE 的延长线于点F ，∴△AEF∽△BED.∴AE BE ＝AF BD. ∵AE＝14AB ， ∴AE＝13BE.∴AF＝13BD. 由AF∥CD，AM ＝MC ，易证得△AFM≌△CDM.∴AF＝CD.∴CD＝13BD.∴BC＝2CD. 点拨：由已知线段的比，求证另外两线段的比，通常添加平行线，构造相似三角形来求解．中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．已知点A、B、C是直径为6cm的⊙O上的点，且AB=3cm，AC=32cm，则∠BAC的度数为（）A．15°B．75°或15°C．105°或15°D．75°或105°【答案】C【解析】解：如图1．∵AD为直径，∴∠ABD=∠ACD=90°．在Rt△ABD中，AD=6，AB=3，则∠BDA=30°，∠BAD=60°．在Rt△ABD中，AD=6，AC=32，∠CAD=45°，则∠BAC=105°；如图2，．∵AD为直径，∴∠ABD=∠ABC=90°．在Rt△ABD中，AD=6，AB=3，则∠BDA=30°，∠BAD=60°．在Rt△ABC中，AD=6，AC=32，∠CAD=45°，则∠BAC=15°．故选C．点睛：本题考查的是圆周角定理和锐角三角函数的知识，掌握直径所对的圆周角是直径和熟记特殊角的三角函数值是解题的关键，注意分情况讨论思想的运用．2．《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（）A．11910813x yy x x y=⎧⎨+-+=⎩（）（）B．108 91311y x x y x y+=+⎧⎨+=⎩C．91181013x yx y y x （）（）=⎧⎨+-+=⎩D．91110813 x yy x x y=⎧⎨+-+=⎩（）（）【答案】D【解析】根据题意可得等量关系：①9枚黄金的重量=11枚白银的重量；②（10枚白银的重量+1枚黄金的重量）-（1枚白银的重量+8枚黄金的重量）=13两，根据等量关系列出方程组即可．【详解】设每枚黄金重x 两，每枚白银重y 两，由题意得：91110813x y y x x y =⎧⎨+-+=⎩（）（）， 故选：D ．【点睛】此题主要考查了由实际问题抽象出二元一次方程组，关键是正确理解题意，找出题目中的等量关系． 3．如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，并且OA=5，OC=1．若把矩形OABC 绕着点O 逆时针旋转，使点A 恰好落在BC 边上的A 1处，则点C 的对应点C 1的坐标为（ ）A ．（﹣91255，）B ．（﹣12955，）C ．（﹣161255，）D ．（﹣121655，） 【答案】A 【解析】直接利用相似三角形的判定与性质得出△ONC 1三边关系，再利用勾股定理得出答案．【详解】过点C 1作C 1N ⊥x 轴于点N ，过点A 1作A 1M ⊥x 轴于点M ，由题意可得：∠C 1NO=∠A 1MO=90°，∠1=∠2=∠1，则△A 1OM ∽△OC 1N ，∵OA=5，OC=1，∴OA 1=5，A 1M=1，∴OM=4，∴设NO=1x ，则NC 1=4x ，OC 1=1，则（1x ）2+（4x ）2=9，解得：x=±35（负数舍去），则NO=95，NC 1=125， 故点C 的对应点C 1的坐标为：（-95，125）． 故选A ．【点睛】此题主要考查了矩形的性质以及勾股定理等知识，正确得出△A 1OM ∽△OC 1N 是解题关键．4．如图，在平面直角坐标中，正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形，且相似比为13，点A ，B ，E 在x 轴上，若正方形BEFG 的边长为6，则C 点坐标为（ ）A ．（3，2）B ．（3，1）C ．（2，2）D ．（4，2）【答案】A 【解析】∵正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形，且相似比为13， ∴AD BG =13， ∵BG=6，∴AD=BC=2， ∵AD ∥BG ，∴△OAD ∽△OBG ， ∴OA OB =13， ∴2OA OA +=13， 解得：OA=1，∴OB=3，∴C 点坐标为：（3，2），故选A ．5．下列各式计算正确的是( )A 633=B ．1236=C ．3535+=D 1025=【答案】B【解析】A 63、B 123=36=6，∴本选项正确；C 选项中，∵35=353+5D选项中，∵10102=52÷≠，∴本选项错误；故选B.6．已知，C是线段AB的黄金分割点，AC＜BC，若AB=2，则BC=（）A．3﹣5B．12（5+1）C．5﹣1 D．12（5﹣1）【答案】C【解析】根据黄金分割点的定义，知BC为较长线段；则BC=512-AB，代入数据即可得出BC的值．【详解】解：由于C为线段AB=2的黄金分割点，且AC＜BC，BC为较长线段；则BC=2×512-=5-1．故答案为：5-1．【点睛】本题考查了黄金分割，应该识记黄金分割的公式：较短的线段=原线段的352倍，较长的线段=原线段的512-倍．7．如图，小正方形边长均为1，则下列图形中三角形(阴影部分)与△ABC相似的是A．B．C．D．【答案】B【解析】根据网格的特点求出三角形的三边，再根据相似三角形的判定定理即可求解. 【详解】已知给出的三角形的各边AB、CB、AC2、210、只有选项B的各边为125B．【点晴】此题主要考查相似三角形的判定，解题的关键是熟知相似三角形的判定定理.8．在△ABC中，AB=AC=13，BC=24，则tanB等于（）A．513B．512C．1213D．125【答案】B【解析】如图，等腰△ABC 中，AB=AC=13，BC=24，过A 作AD ⊥BC 于D ，则BD=12，在Rt △ABD 中，AB=13，BD=12，则， 225AB BD -=，故tanB=512AD BD =. 故选B ． 【点睛】考查的是锐角三角函数的定义、等腰三角形的性质及勾股定理．9．学完分式运算后，老师出了一道题“计算：23224x x x x +-++-”. 小明的做法：原式222222(3)(2)26284444x x x x x x x x x x x +--+----=-==----； 小亮的做法：原式22(3)(2)(2)624x x x x x x x =+-+-=+-+-=-； 小芳的做法：原式32313112(2)(2)222x x x x x x x x x x +-++-=-=-==++-+++． 其中正确的是（ ）A ．小明B ．小亮C ．小芳D ．没有正确的【答案】C 【解析】试题解析：23224x x x x +-++- =()()32222x x x x x +--++- =3122x x x +-++ =3-12x x ++ =22x x ++ =1．所以正确的应是小芳．故选C ．10．如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是( )A ．1，2，3B ．1，12C ．1，13D ．1，23【答案】D【解析】根据三角形三边关系可知，不能构成三角形，依此即可作出判定； B 、根据勾股定理的逆定理可知是等腰直角三角形，依此即可作出判定； C 、解直角三角形可知是顶角120°，底角30°的等腰三角形，依此即可作出判定； D 、解直角三角形可知是三个角分别是90°，60°，30°的直角三角形，依此即可作出判定． 【详解】∵1+2=3，不能构成三角形，故选项错误； B 、∵12+12=(2)2，是等腰直角三角形，故选项错误； C 、底边上的高是2231-2（）=12，可知是顶角120°，底角30°的等腰三角形，故选项错误； D 、解直角三角形可知是三个角分别是90°，60°，30°的直角三角形，其中90°÷30°=3，符合“智慧三角形”的定义，故选项正确． 故选D ．二、填空题（本题包括8个小题）11．在临桂新区建设中，需要修一段全长2400m 的道路，为了尽量减少施工对县城交通工具所造成的影响，实际工作效率比原计划提高了20%，结果提前8天完成任务，求原计划每天修路的长度．若设原计划每天修路xm ，则根据题意可得方程 ．【答案】()240024008.120%x x -=+. 【解析】试题解析：∵原计划用的时间为：2400x， 实际用的时间为：()2400120%x +， ∴可列方程为：()240024008.120%x x -=+ 故答案为()240024008.120%x x-=+ 12．如图，在边长相同的小正方形网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB 与CD 相交于点P ，则tan ∠APD 的值为______.【答案】1【解析】首先连接BE ，由题意易得BF=CF ，△ACP ∽△BDP ，然后由相似三角形的对应边成比例，易得DP ：CP=1：3，即可得PF ：CF=PF ：BF=1：1，在Rt △PBF 中，即可求得tan ∠BPF 的值，继而求得答案．【详解】如图：，连接BE，∵四边形BCED是正方形，∴DF=CF=CD，BF=BE，CD=BE，BE⊥CD，∴BF=CF，根据题意得：AC∥BD，∴△ACP∽△BDP，∴DP：CP=BD：AC=1：3，∴DP：DF=1：1，∴DP=PF=CF=BF，在Rt△PBF中，tan∠BPF==1，∵∠APD=∠BPF，∴tan∠APD=1．故答案为：1【点睛】此题考查了相似三角形的判定与性质，三角函数的定义．此题难度适中，解题的关键是准确作出辅助线，注意转化思想与数形结合思想的应用．13．一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同，随机摸出两个小球，摸出两个颜色相同的小球的概率为____.【答案】2 5【解析】解：根据题意可得：列表如下红1 红2 黄1 黄2 黄3红1 红1，红2 红1，黄1 红1，黄2 红1，黄3 红2 红2，红1 红2，黄1 红2，黄2 红2，黄3 黄1 黄1，红1 黄1，红2 黄1，黄2 黄1，黄3黄2 黄2，红1 黄2，红2 黄2，黄1黄2，黄3 黄3黄3，红1黄3，红2黄3，黄1黄3，黄2共有20种所有等可能的结果，其中两个颜色相同的有8种情况， 故摸出两个颜色相同的小球的概率为82205=． 【点睛】本题考查列表法和树状图法，掌握步骤正确列表是解题关键．14．如图，某小型水库栏水坝的横断面是四边形ABCD ，DC ∥AB ，测得迎水坡的坡角α=30°，已知背水坡的坡比为1.2：1，坝顶部DC 宽为2m ，坝高为6m ，则坝底AB 的长为_____m ．【答案】（7+63）【解析】过点C 作CE ⊥AB ，DF ⊥AB ，垂足分别为：E ，F ，得到两个直角三角形和一个矩形，在Rt △AEF 中利用DF 的长，求得线段AF 的长；在Rt △BCE 中利用CE 的长求得线段BE 的长，然后与AF 、EF 相加即可求得AB 的长．【详解】解：如图所示：过点C 作CE ⊥AB ，DF ⊥AB ，垂足分别为：E ，F ，∵坝顶部宽为2m ，坝高为6m ， ∴DC=EF=2m ，EC=DF=6m ， ∵α=30°， ∴BE=63tan30EC=︒（m ），∵背水坡的坡比为1.2：1， ∴1.2 1.21DF AF AF ==， 解得：AF=5（m ），则3（3m ， 故答案为（3m ． 【点睛】本题考查了解直角三角形的应用，解题的关键是利用锐角三角函数的概念和坡度的概念求解．15．在不透明的口袋中有若干个完全一样的红色小球，现放入10个仅颜色不同的白色小球，均匀混合后，有放回的随机摸取30次，有10次摸到白色小球，据此估计该口袋中原有红色小球个数为_____． 【答案】20【解析】利用频率估计概率，设原来红球个数为x 个，根据摸取30次，有10次摸到白色小球结合概率公式可得关于x 的方程，解方程即可得. 【详解】设原来红球个数为x 个， 则有1010x +=1030， 解得，x=20，经检验x=20是原方程的根. 故答案为20. 【点睛】本题考查了利用频率估计概率和概率公式的应用，熟练掌握概率的求解方法以及分式方程的求解方法是解题的关键.16．如图，矩形ABCD ，AB=2，BC=1，将矩形ABCD 绕点A 顺时针旋转90°得矩形AEFG ，连接CG 、EG ，则∠CGE=________．【答案】45° 【解析】试题解析：如图，连接CE ， ∵AB=2，BC=1， ∴DE=EF=1，CD=GF=2， 在△CDE 和△GFE 中,CD GF CDE GFE DE EF =⎧⎪∠=∠⎨⎪=⎩∴△CDE ≌△GFE(SAS)，∴CE=GE ，∠CED=∠GEF ， 90AEG GEF ∠+∠=， 90CEG AEG CED ∴∠=∠+∠=，45.CGE ∴∠=故答案为45.17．一元二次方程x 2+mx+3=0的一个根为- 1，则另一个根为 ． 【答案】-1.【解析】因为一元二次方程的常数项是已知的，可直接利用两根之积的等式求解． 【详解】∵一元二次方程x 2+mx+1=0的一个根为-1，设另一根为x 1， 由根与系数关系：-1•x 1=1， 解得x 1=-1． 故答案为-1.18．如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是（3，-1）和（-3，1），那么“卒”的坐标为_____.【答案】（-2，-2）【解析】先根据“相”和“兵”的坐标确定原点位置，然后建立坐标系，进而可得“卒”的坐标． 【详解】“卒”的坐标为（﹣2，﹣2），故答案是：（﹣2，﹣2）． 【点睛】考查了坐标确定位置，关键是正确确定原点位置． 三、解答题（本题包括8个小题） 19．先化简，再求值：22211·1441x x x x x x -++--+-，其中x 是从-1、0、1、2中选取一个合适的数． 【答案】12-.【解析】先把分子分母因式分解，约分后进行通分化为同分母，再进行同分母的加法运算，然后再约分得到原式=12x -，由于x 不能取±1，2，所以把x=0代入计算即可． 【详解】22211·1441x x x x x x -++--+-, =()()2211•11(2)1x x x x x x -+++--- =12(1)(2)(1)(2)x x x x x -+----=()()112x x x ---=12x -， 当x=0时，原式=11022=--. 20．如图，某校教学楼AB 的后面有一建筑物CD ，当光线与地面的夹角是22º时，教学楼在建筑物的墙上留下高2m 的影子CE ；而当光线与地面的夹角是45º时，教学楼顶A 在地面上的影子F 与墙角C 有13m 的距离(B 、F 、C 在一条直线上)．求教学楼AB 的高度；学校要在A 、E 之间挂一些彩旗，请你求出A 、E 之间的距离(结果保留整数)． 【答案】（1）2m （2）27m【解析】（1）首先构造直角三角形△AEM ，利用0AMtan22ME=，求出即可． （2）利用Rt △AME 中，0MEcos22AE=，求出AE 即可． 【详解】解：（1）过点E 作EM ⊥AB ，垂足为M ．设AB 为x ．在Rt △ABF 中，∠AFB=45°， ∴BF=AB=x ， ∴BC=BF ＋FC=x ＋1．在Rt △AEM 中，∠AEM=22°，AM=AB －BM=AB －CE=x －2， 又∵0AM tan22ME =，∴x 22x 135-≈+，解得：x≈2． ∴教学楼的高2m ．（2）由（1）可得ME=BC=x+1≈2+1=3． 在Rt △AME 中，0MEcos22AE=， ∴AE=MEcos22°≈15252716⨯≈． ∴A 、E 之间的距离约为27m ． 21．如图，二次函数的图像与轴交于、两点，与轴交于点，．点在函数图像上，轴，且，直线是抛物线的对称轴，是抛物线的顶点．求、的值；如图①，连接，线段上的点关于直线的对称点恰好在线段上，求点的坐标；如图②，动点在线段上，过点作轴的垂线分别与交于点，与抛物线交于点．试问：抛物线上是否存在点，使得与的面积相等，且线段的长度最小？如果存在，求出点的坐标；如果不存在，说明理由．【答案】（1），；（2）点的坐标为；（3）点的坐标为和【解析】（1）根据二次函数的对称轴公式，抛物线上的点代入，即可；（2）先求F 的对称点，代入直线BE ，即可；（3）构造新的二次函数，利用其性质求极值. 【详解】解：（1）轴，，抛物线对称轴为直线点的坐标为解得或（舍去）， （2）设点的坐标为对称轴为直线点关于直线的对称点的坐标为.直线经过点利用待定系数法可得直线的表达式为.因为点在上，即点的坐标为（3）存在点满足题意.设点坐标为，则作垂足为①点在直线的左侧时，点的坐标为点的坐标为点的坐标为在中，时，取最小值.此时点的坐标为②点在直线的右侧时，点的坐标为同理，时，取最小值.此时点的坐标为综上所述：满足题意得点的坐标为和考点：二次函数的综合运用.22．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A作BC的平行线交CE的延长线与F，且AF=BD，连接BF。

一、相似的有关概念1．相似形具有相同形状的图形叫做相似形．相似形仅是形状相同，大小不一定相同．相似图形之间的互相变换称为相似变换． 2．相似图形的特性两个相似图形的对应边成比例，对应角相等． 3．相似比两个相似图形的对应角相等，对应边成比例．二、相似三角形的概念1．相似三角形的定义对应角相等，对应边成比例的三角形叫做相似三角形．如图，ABC △与A B C '''△相似，记作ABC A B C '''△∽△，符号∽读作“相似于”．A 'B 'C 'CB A2．相似比相似三角形对应边的比叫做相似比．全等三角形的相似比是1．“全等三角形”一定是“相似形”，“相似形”不一定是“全等形”．三、相似三角形的性质1．相似三角形的对应角相等如图，ABC △与A B C '''△相似，则有A A B B C C '''∠=∠∠=∠∠=∠，，． A 'B 'C 'CB A知识点睛 相似三角形的性质2．相似三角形的对应边成比例 如图，ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）． A 'B 'C 'CB A3．相似三角形的对应边上的中线，高线和对应角的平分线成比例，都等于相似比．如图1，ABC △与A B C '''△相似，AM 是ABC △中BC 边上的中线，A M ''是A B C '''△中B C ''边上的中线，则有AB BC AC AMk A B B C A C A M ====''''''''（k 为相似比）． M 'MA 'B 'C 'C BA图1如图2，ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AHk A B B C A C A H ====''''''''（k 为相似比）． H 'H AB C C 'B 'A '图2如图3，ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC ADk A B B C A C A D ====''''''''（k 为相似比）．D 'D A 'B C 'C B A图34．相似三角形周长的比等于相似比．如图4，ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++．A 'B 'C 'CB A图45．相似三角形面积的比等于相似比的平方．如图5，ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AHk A B B C A C A H====''''''''（k 为相似比）．进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．H 'H AB C C 'B 'A '图5四、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似．2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似．五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有“三点定形法”． 1．横向定型法 欲证AB BCBE BF =，横向观察，比例式中的分子的两条线段是AB 和BC ，三个字母A B C ，，恰为ABC △的顶点；分母的两条线段是BE 和BF ，三个字母B E F ，，恰为BEF △的三个顶点．因此只需证ABC EBF △∽△．2．纵向定型法欲证AB DEBC EF=，纵向观察，比例式左边的比AB 和BC 中的三个字母A B C ，，恰为ABC △的顶点；右边的比两条线段是DE 和EF 中的三个字母D E F ，，恰为DEF △的三个顶点．因此只需证ABC DEF △∽△． 3．中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况，此时可考虑运用等线，等比或等积进行变换后，再考虑运用三点定形法寻找相似三角形．这种方法就是等量代换法．在证明比例式时，常用到中间比．比例中项式的证明，通常涉及到与公共边有关的相似问题。