反比例函数中K的几何意义 (1)

反比例函数K的几何意义反比例函数是一种特殊的数学函数形式，具有形如y=k/x的表达式，其中k是一个常数。

在这个函数中，x和y之间存在一种特殊的关系：当x增大时，y会减小，反之亦然。

因此，反比例函数的几何意义可以通过分析函数图像和实际例子来理解。

首先，我们可以通过绘制反比例函数的图像来揭示其几何意义。

考虑一个简单的例子：y=1/x。

对于这个函数，我们可以观察到以下几个重要的特点：1.图像总是通过第一象限的正半轴和第三象限的负半轴。

这是因为除数不能为零，所以函数在x=0时无定义。

2.图像与两条坐标轴的交点确定了函数的极值点：当x趋近于正无穷或负无穷时，y趋近于零。

这也表示当x趋近于零时，y趋近于正或负无穷。

3.图像是关于y=x和y=-x的直线对称的。

这是因为当x和y的值交换时，函数的值保持不变。

通过上述特点，我们可以揭示反比例函数的几何意义。

函数的图像形状类似于一组双曲线的分支，其中的曲线与两条坐标轴无法相交，而它们的渐近线分别与坐标轴平行。

这暗示了反比例函数的一个重要特点：随着一个变量的增加，另一个变量会减少。

例如，在y=1/x的情况下，我们可以看到当x增加时，y会减小。

1.电阻和电流：欧姆定律表明电阻与电流成反比例关系。

当电流增大时，电阻减小。

这可以解释为，当电阻较低时，电流可以更容易地通过电路，导致电流增加。

2.时间和任务完成率：假设一个人在一段时间内完成了一定数量的任务。

如果任务数量保持不变，增加时间将导致任务完成率降低。

这是因为在更长的时间内，完成的任务数量将更少。

3.运动速度和到达时间：当我们维持一定的目的地距离不变时，提高行驶速度将缩短到达目的地所需的时间。

这是因为较高的行驶速度意味着我们每单位时间所覆盖的距离更多。

这些例子揭示了反比例函数在现实生活中的广泛应用，从电路设计到时间管理，以及交通规划等等。

通过理解反比例函数的几何意义，我们可以更好地理解和应用这个数学概念。

总而言之，反比例函数是一种数学函数形式，其几何意义可以通过分析函数图像和实际例子来理解。

专题01 用几何意义探究反比例函数中k 值问题的多种解法如图，反比例函数k y x =（k >0），A 、C 是第一象限上两点，S △OAB =S △OCD =2k ；S △OAC =S 梯形ABDC 在已知面积或比例线段解答反比例函数的问题中，善于利用k 与面积的关系，往往可以事半功倍．典例1．知面积比值，求k 值（2022•山东聊城中考真题）如图，直线与反比例函数在第一象限内的图象交于点，与y 轴交于点B ，过双曲线上的一点C 作x 轴的垂线，垂足为点D ，交直线于点E ，且．()30y px p =+¹()0k y k x=>()2,A q 3y px =+:3:4AOB COD S S =△△(1)求k ，p 的值；(2)若OE 将四边形BOCE 分成两个面积相等的三角形，求点C 的坐标．【答案】(1)，；(2)点C 的坐标为(4，2)【解析】【方法一】坐标法（1）解：∵直线与y 轴交点为B ，∴，即．∵点A 的横坐标为2，∴．∵，∴△COD 的面积为4，设，∴，解得．∵点在双曲线上，∴，把点代入，得，∴，；8k =12p =3y px =+()0,3B 3OB =13232AOB S =´´=V :3:4AOB COD S S =△△,k C m m æöç÷èø142k m m×=8k =()2,A q 8y x=4q =()2,4A 3y px =+12p =8k =12p =（2）解：由（1）得8,C m m æöç÷èø，∴．∵OE 将四边形BOCE 分成两个面积相等的三角形，∴，∵32BOE S m =△，，∴，解得或（不符合题意，舍去），∴点的坐标为（4，2）．【方法二】k 的几何意义法解：（1）由题意知，△ABO 的面积为3，又，得：△OCD 的面积为4，故k =2S △OCD =8，所以，A （2,4），把点代入，得（2）如图，过A ，E 作y 轴垂线，垂足为M ，N则四边形ODEN 为矩形，所以，S △OEN =S △OED ，又S △OBE =S △OCE ，所以S △BEN =S △OCD =4，1,32E m m æö+ç÷èøBOE COE S S =△△13422COE m S m æö=+-ç÷èø△3134222m m m æö=+-ç÷èø4m =4m =-C :3:4AOB COD S S =△△()2,4A 3y px =+12p =所以S △ABM =1，∵AM ∥NE ，∴△ABM ∽△EBN ，其面积比为1:4，∴AM ：NE =1:2，即NE =4，∴C 点坐标为（4,2）典例2．知比例线段，求k 值（2022•贵州铜仁中考真题）如图，点A 、B 在反比例函数k y x=的图象上，AC y ^轴，垂足为D ，BC AC ^．若四边形AOBC 的面积为6，12AD AC =，则k 的值为_______．【答案】3．【解析】【方法一】坐标法设点,k A a a æöç÷èø，∵AC y ^轴，∴AD a =，k OD a =，∵12AD AC =，∴AC 2a =，∴CD =3a ，∵BC AC ^．AC y ^轴，∴BC ∥y 轴，∴点B 3,3æöç÷èøk a a ，∴233k k k BC a a a=-=，∵AOD AOBC OBCD S S S =+V 四边形梯形，四边形AOBC 间面积为6，∴12136232k k a k a a æö+´=+ç÷èø，解得：3k =．【方法二】k 的几何意义法如图，连接OC ，延长CB 交x 轴于E ，则S △AOD =S △BOE =12k ，因为AD ：AC =1:2，所以S △AOC =2S △AOD =k ，S △BOC =6-k ，又四边形DOEC 为矩形，OC 为对角线，所以，S △COD =S △COE ，所以12k +k =6-k +12k ，解得：k =3．典例3．知面积值，求k 值（2022•内蒙古呼伦贝尔中考真题）如图，在平面直角坐标系中，Rt OAB △的直角顶点B 在x 轴的正半轴上，点O 与原点重合，点A 在第一象限，反比例函数k y x=（0x >）的图象经过OA 的中点C ，交AB 于点D ，连接CD ．若ACD △的面积是1，则k 的值是_________．【答案】43．【解析】【方法一】坐标法解：设C （m ，k m），因为C 为OA 中点，所以A （2m ，2k m），则D （2m ，2k m ），又△ACD 的面积为1，所以12122k k m m m æö×-=ç÷èø，解得：k =43【方法二】k 的几何意义法解：连接OD ，过C 作CE AB ∥，交x 轴于E ，∵∠ABO ＝90°，反比例函数k y x =（x ＞0）的图象经过OA 的中点C ，1ACD S =V ，∴12COE BOD S S k ==△△，1ACD OCD S S ==V V ，2OC =OA ，∵CE AB ∥，∴△OCE ∽△OAB ，∴221124OCE S OC S OA æöæö===ç÷ç÷èøèø△△O A B ，∴4OCE OAB ACD OCD OBD S S S S S ==++V V V V V ，∴1141122k k ´=++，∴k ＝43，故答案为：43．1.（2022•辽宁锦州中考真题）如图，在平面直角坐标系中，△AOB 的边OB 在y 轴上，边AB 与x 轴交于点D ，且BD =AD ，反比例函数y =k x(x >0)的图像经过点A ，若S △OAB =1，则k 的值为___________．【答案】2．【解析】【方法一】坐标法解：设A(a，b) ，如图，作A过x轴的垂线与x轴交于C，则：AC=b，OC=a，AC∥OB，∴∠ACD=∠BOD=90°，∠ADC=∠BDO，∴△ADC≌△BDO，∴S△ADC=S△BDO，∴S△OAC=S△AOD+ S△ADC=S△AOD+ S△BDO= S△OAB=1，∴12×OC×AC=12ab=1，∴ab=2，∵A(a，b) 在y=kx上，∴k=ab=2 ．【方法二】k的几何意义法由上知，S△AOC=1，所以，k=2S△AOC=2故答案为：2．2.（2022•辽宁鞍山中考真题）如图，在平面直角坐标系中，O 是坐标原点．在Rt OAB V 中，90OAB Ð=°，边OA 在y 轴上，点D 是边OB 上一点，且:1:2OD DB =，反比例函数()0ky x x=>的图象经过点D 交AB 于点C ，连接OC ．若4OBC S =△，则k 的值为_________．【答案】1．【解析】【方法一】坐标法解：∵反比例函数()0k y x x=>的图象经过点D ，∠OAB ＝90°，∴D （m ，k m ），∵OD ：DB ＝1：2，∴B （3m ，3k m），∴AB ＝3m ，OA ＝3k m ，∴反比例函数()0k y x x =>的图象经过点D 交AB 于点C ，∠OAB ＝90°，∴12AOC S k =△，∵4OBC S △＝，∴4AOB AOC S S -△△＝，即1313422k m k m ´×-=，解得k ＝1【方法二】k 的几何意义法如图，过D 作DE ⊥x 轴，则DE ∥AB ，因为OD ：BD =1:2，所以DE ：AB =1:3，所以S △ODE ：S △OAB =1：9，又S △ODE =S △OAC =12k ，所以12k +4=92k ，解得：k =13.（2022•江苏南通中考真题）平面直角坐标系中，已知点是函数图象上的三点．若，则k 的值为___________．【答案】【解析】【方法一】坐标法解：∵点是函数图象上的三点，∴，，∴m ＝n ，∴，，∴点B 、C 关于原点对称，∴设直线BC 的解析式为，代入得：，解得：，∴直线BC 的解析式为，xOy (,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x=¹2ABC S =△34(,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x =¹260k m =>6k mn =(3,2)B m m (3,2)C m m --()0y kx k =¹(3,2)B m m 23m mk =23k =23y x =不妨设m ＞0，如图，过点A 作x 轴的垂线交BC 于D ，把x ＝m 代入得：，∴D （m ，），∴AD ＝，∴，∴，∴，而当m ＜0时，可得，故答案为：．【方法二】由题意知，S △OAB =12632m n m m ×-×，O 为BC 中点，因为所以，S △OAB =12632m n m m ×-×=1，即291mn m -=①，又632m m m n k ×=×=②，23y x =23y m =23m 216633m m m -=()11633223ABC S m m m =´×+=V 218m =2136684k m ==´=34k =342ABC S =△由①②可得：4.（2022•湖北十堰中考真题）如图，正方形ABCD 的顶点分别在反比例函数()110k y k x=>和()220k y k x =>的图象上．若BD y ∥轴，点D 的横坐标为3，则12k k +=（ ）A ．36B ．18C ．12D ．9【答案】B ．【解析】【方法一】解：连接AC ，与BD 相交于点P ，设PA =PB =PC =PD =t （t ≠0）．∴点D 的坐标为（3，23k ），∴点C 的坐标为（3-t ，23k +t ）．∵点C 在反比例函数y =2k x 的图象上，34k=∴（3-t ）（23k +t ）=k 2，化简得：t =3-23k ，∴点B 的纵坐标为23k +2t =23k +2（3-23k ）=6-23k ，∴点B 的坐标为（3，6-23k ），∴3×（6-23k ）=1k ，整理，得：1k +2k =18．【方法二】先利用D 点坐标，表示出A 和C 点坐标，再根据四边形ABCD 为正方形，BD 与y 轴平行，知AC 平行于x 轴，那么，A 和C 点的纵坐标相等，进而求解23,3k D æöç÷èø，13,3k B æöç÷èø，122123,636k k k C k k æöç÷--ç÷-ç÷-èø，121123,636k k k A k k æöç÷-+ç÷-ç÷+èø所以2112123366k k k k k k =---+，整理得：()212212180k k k k ---=即()()1212108k k k k -+=-因为()120k k -¹所以()12018k k +-=，即1218k k +=5.（2022•黑龙江龙东中考真题）如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x=的图象上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（ ）A ．2B ．1C ．1-D ．2-【答案】D ．【解析】解：设B点坐标为3,mmæöç÷èø，则A3,3kmmæöç÷èø，因为平行四边形OBAD的面积是5，所以353kmmmæö-×=ç÷èø，解得k=-2【方法二】解：如图，连接OA，设AB交y轴于点C，∵四边形OBAD是平行四边形，平行四边形OBAD的面积是5，∴1522AOB OBADS S==V Y，AB∥OD，∴AB⊥y轴，∵点B在反比例函数3yx=的图象上，顶点A在反比例函数kyx=的图象上，∴3,22 COB COAkS S==-V V，∴35222 AOB COB COAkS S S=+=-=V V V，解得：2k=-．故选：D．6.（2022•湖北黄石中考真题）如图，反比例函数kyx=的图象经过矩形ABCD对角线的交点E和点A，点B、C在x轴上，OCE△的面积为6，则k=______________．【答案】8．【解析】设C （m ，0），由题意知E 为AC 中点，因为△OCE 面积为6，所以E 点纵坐标为12m，所以E 12,12km m æöç÷èø，A 24,6km m m æö-ç÷èø，又A 在反比例函数图像上所以246km m k mæö-×=ç÷èø解得k =8【方法二】解：如图作EF ⊥BC ，则12EF AB =，设E 点坐标为（a ，b ），则A 点的纵坐标为2b ，则可设A 点坐标为（c ，2b ），∵点A ，E 在反比例函数k y x=上，∴ab =k =2bc ，解得：a =2c ，故BF =FC =2c -c =c ，∴OC =3c ，故113622OEC S OC EF c b =´´=´´=V ，解得：bc =4，∴k =2bc =8，故答案为：8．7.（2022•贵州六盘水中考真题）如图，正比例函数与反比例函数的图象交于，两点．y x =4y x=A B(1)求，两点的坐标；(2)将直线向下平移个单位长度，与反比例函数在第一象限的图象交于点，与轴交于点，与轴交于点，若，求的值．【答案】(1)；(2)【解析】（1）解：联立与，解得，；（2）【方法一】解：如图，过点作轴于点，A B y x =a C x D y E 13CD DE =a ()()2,2,2,2A B --3a =y x =4y x=121222,22x x y y ==-ììíí==-îî()()2,2,2,2A B \--C CF y ^F，，，直线向下平移个单位长度得到，根据图象可知,令，得，令，得，，，，，与反比例函数在第一象限的图象交于点，，将代入，得，解得或（舍去）．【方法二】CF OD \∥Q 13CD DE =13OF CD OE DE \==Q y x =a y x a =-0a >0x =y a =-0y =x a =()0,E a \-(),0D a 10,3F a æö\ç÷èø13c y a \=Q y x a =-4y x=C 41213c x aa \==121,3C a a æöç÷èøy x a =-1123a a a=-3a =3a =-如图，连接OC ，过C 作CE ⊥x 轴，因为CD ：DE =1:3，CE ∥OE则△CDE ∽△EDO ，相似比为1:3，面积比为1:9，易知△ODE 面积为212a ，△OCE 的面积为12k =2，所以△OCD 的面积为2-2118a ，又△OCD 与△ODE 的面积比为1:3，所以2-2118a =21132a ´，解得：a =3或a =-3（舍）8.（2022•安徽中考真题）如图，平行四边形OABC 的顶点O 是坐标原点，A 在x 轴的正半轴上，B ，C 在第一象限，反比例函数1y x =的图象经过点C ，()0k y k x=¹的图象经过点B ．若OC AC =，则k =________．【答案】3．【解析】【方法一】设C 1,m m æöç÷èø，因为OC =AC所以A ()2,0m ，又OABC 为平行四边形所以B 13,m m æöç÷èø因为B 点在k y x =上，所以k =133m m ×=【方法二】解：过点C 作CD ⊥OA 于D ，过点B 作BE ⊥x 轴于E ，∴CD ∥BE ，∵四边形ABCO 为平行四边形，∴CB OA ∥ ，即CB DE ∥，OC =AB ，∴四边形CDEB 为平行四边形，∵CD ⊥OA ，∴四边形CDEB 为矩形，∴CD =BE ，∴在Rt △COD 和Rt △BAE 中，OC AB CD EB =ìí=î，∴Rt △COD ≌Rt △BAE （HL ），∴S △OCD =S △ABE ，∵OC =AC ，CD ⊥OA ，∴OD =AD ，∵反比例函数1yx=的图象经过点C，∴S△OCD=S△CAD=12，∴S平行四边形OCBA=4S△OCD=2，∴S△OBA=11 2OCBAS=平行四边形，∴S△OBE=S△OBA+S△ABE=13122+=，∴3232k=´=．故答案为3．。

反比例函数中k的几何意义的应用
k在反比例函数中具有重要的几何意义，以下列举一些它的应用。

1. 直线反比例函数：k反映直线斜率的倒数，即斜率m=-k。

当给定直
线k值时，由定点和k值可以求出斜率m，从而可以绘制出这条直线。

2. 圆反比例函数：k反映圆半径r的倒数，即r=1/k。

当给定圆k值时，由定点和k值可以求出圆半径，从而可以绘制出这个圆。

3. 抛物线反比例函数：k反映抛物线的开口方向，当k > 0时，抛物线
向右开口；当k < 0时，抛物线向左开口。

4. 双曲线反比例函数：k反映双曲线的开口方向，当k＞0时，双曲线
开口向右；当k＜0时，双曲线开口向左。

5. 其他函数反比例函数：k可以反映此类函数中曲线的凹凸，当k > 0时，曲线是凹曲线；当k < 0时，曲线是凸曲线。

总之，k在反比例函数中应用广泛，几乎所有的函数都可以用反比例函
数表示。

它的几何意义非常重要，不仅仅可以根据k值绘制出各种曲线，而且可以了解曲线的开口方向以及凹凸方向。

因此，k在反比例函
数绘制中发挥着重要的作用。

专题反比例函数中k的几何意义及应用研究函数问题要透视函数的本质特征。

反比例函数中，比例系数k有一个很重要的几何意义，那就是：过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N（如图1所示），则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。

所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数。

从而有。

在解有关反比例函数的问题时，若能灵活运用反比例函数中k的几何意义，会给解题带来很多方便。

现举例说明。

应用一：比较面积大小例1、如图2，在函数（x>0）的图象上有三点A、B、C。

过这三点分别向x轴、y轴作垂线。

过每一点所作的两条垂线与x轴、y轴围成的矩形的面积分别为，则（）。

A、 B、C、 D、解：根据反比例函数中k的几何意义可知。

所以。

故选D。

应用二：求面积例2、若函数与函数的图象相交于A、C两点，AB垂直x轴于B，则△ABC的面积为（）。

A、1B、2C、kD、分析：如图3，若先求出A、C两点的坐标，再求△ABC的面积，则解题过程复杂烦琐。

若能利用反比例函数中k的几何意义来解，则快刀斩乱麻。

解：由反比例函数图象关于原点成中心对称知O为AC中点。

根据反比例函数中k的几何意义，有：。

又△ABO与△BOC是等底等高的三角形，∴。

故选A。

应用三：确定解析式例3、如图4，反比例函数与一次函数的图象相交于A点，过A点作AB⊥x轴于点B。

已知，直线与x轴相交于点C。

求反比例函数与一次函数的解析式。

解：由反比例函数中k的几何意义知，故。

又反比例函数图象的一支在第二象限，所以。

从而可知，两个函数的解析式分别为和。

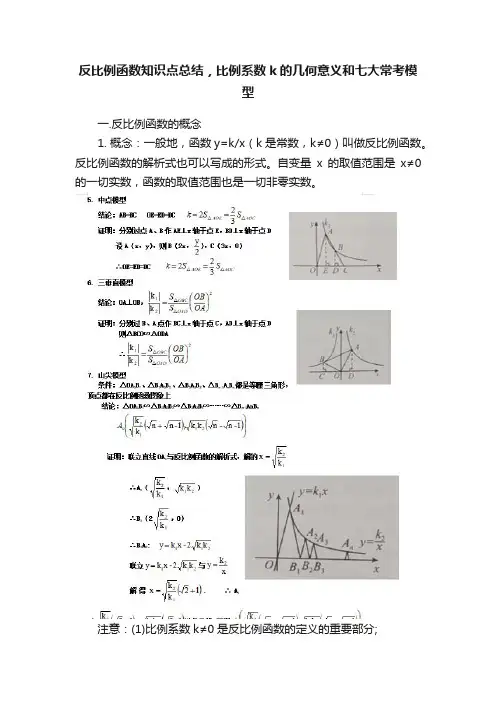
反比例函数知识点总结，比例系数k的几何意义和七大常考模型一.反比例函数的概念1.概念：一般地，函数y=k/x（k是常数，k≠0）叫做反比例函数。

反比例函数的解析式也可以写成的形式。

自变量x的取值范围是x≠0的一切实数，函数的取值范围也是一切非零实数。

注意：(1)比例系数k≠0是反比例函数的定义的重要部分;(2)在反比例函数的解析式中,k,x,y均不等于0;(3)反比例函数中的两个变量一定成反比例关系,反之,则不一定成立例 1 给出的六个关系式:①x(y+1); ②y=2/(x+2); ③y=1/x²;④y=1/2x; ⑤y=x/2 ; ⑥y=-3/x.其中y是x的反比例函数的是 ( )A.①②③④⑥B.③⑤⑥C.①②④D.④⑥例2 若函数是y关于x的反比例函数,则m= .例3 关于正比例函数y=-x/3和反比例函数y=-1/3x的说法正确的是 ( )A.自变量x的指数相同B.比例系数相同C.自变量x的取值范围相同D.函数y的取值范围相同2.易错点解析漏掉k≠0这一条件解答与反比例函数有关的问题时,要注意系数k≠0是反比例函数定义中必不可少的一部分,不能漏掉这一条件.例4已知函数为反比例函数,则k= .二.反比例函数的图像和性质1.反比例函数的图像是双曲线，它有两个分支，这两个分支分别位于第一、三象限，或第二、四象限，它们关于原点对称。

由于反比例函数中自变量x≠0，函数y≠0，所以，它的图像与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。

2.反比例函数的性质注意：y随x变化的情况必须指出“在每个象限内”或“在每一分支上”这一条件。

例5 关于反比例函数y=3/x的图象,下列说法正确的是 ( )A.图象经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小例6.当x<0时,下列表示函数y=-1/x的图象的是 ( ) 例7.下列反比例函数中,图象位于第二、四象限的是( )A.y=2/x B.y=0.2/x C.y=√2/x D.y=-2/5x 例8.对于反比例函数y=(k-√10)/x,在每个象限内,y随x的增大而增大,则满足条件的非负整数k有 ( )A.1个B.2个C.3个D.4个三.反比例函数解析式的确定由于在反比例函数中，只有一个待定系数，因此只需要一对对应值或图像上的一个点的坐标，即可求出k的值，从而确定其解析式。

专题11反比例函数中K的几何意义的两种考法类型一、求比例系数K的值【答案】37-【点睛】本题考查了求反比例函数解析式、相似三角形的判定与性质，直角三角形的性质，解题关键是恰当的作辅助线，构建相似三角形求点的坐标．【答案】2【分析】过点,A C分别作x轴的垂线，垂足分别为可得4EBAE=，设(),A m n，则(,0E mAEO CFB ∴∠=∠90=︒四边形ABCD 是平行四边形,AO BC AO BC∴=∥AOE CBF∴∠=∠AOE CBF∴ ≌AE CF ∴=，OE BF=OB OE OB BF∴-=-即OF EB=CF x ⊥ 轴，C 在4y x=-上，2AEB CFO S S ∴==△△四边形OABC 是正方形，90B ∴∠=︒，45BCA ∠=︒，2BD BE == ，45BDE BED ∴∠=∠=︒，DE BDE BCA ∴∠=∠，【答案】-12【分析】连接OE，CE，过点A作AF⊥x轴，过点与B关于原点对称，再由BE⊥AE，AE为∠km<），由已知条件AC=3DC，DHm）（0得到S△HDC=14S△ADG，所以S△AOC=S△AOF+S梯形【详解】解：连接OE，CE，过点A作AF【点睛】本题考查反比例函数k的几何意义，借助直角三角形和角平分线，将△的面积是解题的关键．【答案】103【分析】根据反比例函数图象上点的坐标特征可得△ABE 和△BCD 的面积，再由【详解】解： 点A ，B 的横坐标分别为(0,)3k D ∴且E 、B 、D 的纵坐标相等，且都为∵点E 在反比例函数8y x=上，1()()2ABE E B A B S x x y y ∆∴=-⨯-⨯∵193ABE BCD S S ∆∆+=，∴8k -类型二、根据比例系数求面积△AOB＝．【答案】12a22ba-【分析】设B（m，b m），A（形的面积可得结论．【详解】解：设B（m，b m），【答案】44150【分析】根据点D 的坐标(2,2m n ∆BEF 的面积．【详解】解：如图，过点D 作DM 在矩形OABC 中，AB OA ⊥，OC AB =，BC OA =，DM AB ∴∥，ΔΔODM OBA ∴∽，:::OD OB DM AB OM OA ∴==．设点D 坐标为(2,2)m n ，其中m ，2OM m ∴=，2DM n =．【变式训练1】已知，如图，双曲线y x=与直线(0)y kx k =>）相交于,A B 两点，AC x ⊥轴于C ，BD x ⊥轴于D ，点E 是AC 的中点，BC 与y 轴相交于点F ，连接,DF DE ，分别与直线y kx =相交于点G 和点H ，则图中阴影部分的面积是________．【答案】8【详解】：连接AD ，如图所示：由,A B 是双曲线12y x=与直线y kx =的交点，易得OA OB =，OC OD =，6AOC BOC BOD AOD S S S S ====△△△△．∴12ABD ABC S S ==△△，∵AC ∥BD ，OF ∥BD ，E 是AC 中点，O 是DC 中点，∴AHE ∆∽BHD ∆，OCF ∆∽DCB ∆，∴12AE AH EH BD HB DH ===，12OF FG OG BD DG BG ===，∴:1:2ADH BDH S S =△△，:1:2BDG DOG S S ∆=△，:1:4AEH BDH S S =△△，1:4AGD BFG S S =△△：，∴2ADH S =△，4BDH S =△，2AHE S =△，∴123DOG BODS S ==△△，∴628ADG AOD DOG S S S =+=+=△△△，∴124BGF ADGS S ==△△，∴12228ABC AEH BGF S S S S =--=--=△△△阴影部分．【变式训练2】如图，平行四边形OABC 的顶点O ，B 在y 轴上，顶点A 在2y x =-上，顶点C 在9y x=上，则平行四边形OABC 的面积是．【答案】11【分析】过点A 作AE y ⊥于点E ，过点C 作CD y ⊥轴于点D ，因为四边形OABC 是平行四边形，可证得四边形OABC 是平行四边形，OA BC AOE CBD ∴=∠=∠，，AE y CD y ⊥⊥ ，，90AEO CDB ∴∠=∠=︒，()AEO CDB AAS ∴ ≌，∴AEO CDB S S = ，【答案】6【分析】设M 点的坐标为1,b b ⎛ ⎝进而求出AOB 的面积．∴MOE AOF ∽，根据反比例函数与三角形的面积关系可得：∴0.5124MOE S S == ，【答案】3【分析】由点C的坐标利用反比例函数图像上点的坐标特征即可求出反比例函数关系式，再根据平行四边形的性质结合点A、O、C的坐标即可求出点可求出点D的坐标，再令反比例函数关系式中的长度，根据三角形的面积公式即可得出结论；【详解】解：∵反比例函数∵点D 为线段AB 的中点，点∴点11(,2)2D ，令4y x=中2y =，则2x =，∴点()2,2P ，∴117222PD =-=，EP ED =12APH AEF CFEA PFEH S S S S S =-=- 矩形四边形四边形DFP DFEH PFEH S S S =- 梯形四边形∵点A 在反比例函数a y x =（0a >，0x >）的图象上，点∴=CFEA S a b a b+=-矩形1【答案】5【分析】作AH⊥OB于H，CE⊥y轴于E，DF∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，【答案】22/122【分析】连接OB交MN于Q，即点Q为OB的中点，过点Q作则22=2OHQk S=△；过点C'作【点睛】本题主要考查了反比例函数比例系数的几何意义，矩形的性质，平行四边形的性质与判定，相似三角形的性质与判定，全等三角形的性质与判定，勾股定理，三角形面积公式，正确作出辅助线是解题的关键．3．如图，P为第一象限内一点，过则S△ABO=．【答案】16【分析】延长BP交x轴于点M，过点设点B12,tt⎛⎫⎪⎝⎭，根据S△BOP=4，可求得ABMN=S△AON+S△AOB，且BOM S△【详解】如图，延长BP交x轴于点则四边形APMN是矩形，∴AP=MN，AN=PM，设点B的横坐标为t，点A，B在函数y=12x上，∴B12,tt⎛⎫ ⎪⎝⎭，∵S△BOP=4，【点睛】此题考查了反比例函数的系数积，正确作出辅助线是解本题的关键．4．如图，点A在函数12( y xx =>轴，且AB＝34AC，则BC＝【答案】5 2【分析】延长CA、BA交坐标轴于数系数k的几何意义得到设A （m ，n ），∵点A 在函数()120y x x =>的图像上，点∴S 四边形CDOF =S 四边形BEOG =18，∴S 四边形AEDC =S 四边形ABGF ，∴AC •m =AB •n ，∵AB =34AC ，∴m =34n ，∴34n •n =12，∴4n =，∴(3,4)A ，【答案】(2，42)【分析】连接OE，根据反比例函数系数n=82m，进一步求得AOB∵反比例函数82(0) y xx=>∴1822AOES=⨯△，42 =，【答案】212022【分析】根据反比例函数上的点向1122331||12OB C OB C OB C S S S k ∆∆∆====形的面积，找出规律即可得出结论．【详解】解：根据题意可知1OB C S ∆（1）若L 过点1T ，则k =（2）若曲线L 使得18T T ～这些点分布在它的两侧，每侧各【答案】4823【分析】（1）由题意可求18T T ～这些点的坐标，将点【答案】②③④【分析】由2OFM kS = 可判断①过A 作AK x ⊥轴于点K ，类比②从而得到OAB ONM ∠=∠可判断【详解】解：①，2k <- ，∴-④，由③可知OA OB ON OM=OAB ONM∴~ OAB ONM∴∠=∠AB NM④正确；故答案为：②③④．【答案】5y x=【分析】利用等积法，得到1,2MF ON MF ON =∥，进而得到AME △的面积，进而得到∴1,4MF AB MF AB =∥，∴AEB FEM ∽，∴::1:4ME BE MF AB ==，∴::1:AME ABE S S ME BE ==【答案】8⊥轴于点N，过点【分析】过点C作CN x()()A aB b，先证明(0,,,0≌MDA OAB【点睛】本题主要考查了反比例函数的图象和性质，三角形全等的判定和性质，等腰直角三角形的性质，解题的关键是掌握反比例函数图象上点的坐标特征，全等三角形对应边相等．【答案】4【分析】过点D作DN⊥Q在反比例函数上，则平行线的判定，得OC∥【详解】过点D作DN⊥【点睛】本题考查反比例函数和几何的综合，解题的关键是掌握反比例函数的图象和性质，矩形的性质，的几何意义．，14．如图，四边形AOBC 边形AOBC 的对角线AB 【答案】185【分析】由CDB ODA ∽5【点睛】本题考查了相似三角形的判定与性质，反比例函数【答案】3215-【分析】根据图形的特点，先求出【详解】+解：如图所示，为4a ；过点D 作DG y ⊥作CF x ⊥轴交于点F ，连接(ΔΔOCD ODG GOFCD S S S =-五边形GOFCD GHCD S S = 五边形直角梯形ΔOCD GHCD S S ∴=直角梯形，()GHCD S GD HC =+⨯直角梯形Δ15OCD GHCD S S ∴==-直角梯形:1:3BD AD = ，ΔΔ:1:3BDO ACD S S ∴=，∵ADC △的面积为3，Δ1BDO S =，ΔΔΔ4OCD BDO ACD S S S ∴=+=∴1548k -=，3215k ∴=-．故答案为：3215-【点睛】本题考查了反比例函数系数于k 的表达式是解本题的关键，综合性较强，难度较大．。

反比例函数函数K的几何意义反比例函数的几何意义是在坐标系中表示直角坐标的一条曲线。

由于该函数的定义域为x≠0，因此在坐标系中，x轴上的原点除外，函数的图像将存在断点。

根据反比例函数的定义，当x的值趋近于零时，x的值将趋近于正无穷大。

同样地，当x的值趋近于正无穷大或负无穷大时，x的值将趋近于零。

这意味着反比例函数的图像将以原点为对称中心，分别在第一、第三象限不断向正无穷大和负无穷大逼近，而在第二、第四象限不断向零逼近。

反比例函数的图像通常表现为一条双曲线，称为反比例双曲线。

该曲线的两个分支在坐标平面中以渐进线（Asymptotes）为边界无限延伸。

渐进线是反比例双曲线的特殊特征，由于两个变量之间的反比例关系，当一个值趋近于无穷大时，另一个值将趋近于零。

因此，反比例双曲线的渐近线是表示这种趋势的标志。

反比例双曲线分为两类：水平渐近线和垂直渐近线。

水平渐近线与x轴平行，表示当x的值趋近于正无穷大或负无穷大时，函数值趋近于零。

垂直渐近线与x轴平行，表示当x的值趋近于零时，函数值趋近于无穷大。

通过做一些简单的数学变换，我们可以将反比例函数的标准形式x=x/x转化为x=xx的形式。

这种形式的反比例函数在坐标系中表示为一条直线。

直线的斜率为x，它表示的是x轴上单位长度对应的x轴上的长度。

当x为正数时，直线向右上方倾斜；当x为负数时，直线向右下方倾斜。

通过改变x的值，可以在坐标系中绘制出不同斜率的直线。

反比例函数的几何意义在数学和物理方面起到了重要的作用。

在数学中，反比例函数的性质使它成为其他函数的重要组成部分，如复合函数、一次函数、二次函数等。

在物理中，许多自然界现象的描述都使用反比例函数，比如电阻和电流之间的关系、浓度和稀释之间的关系、速度和时间之间的关系等。

因此，了解和理解反比例函数的几何意义具有重要的实际应用价值。

专题02 反比例函数中k 的几何意义【知识点梳理】1．反比例函数图象中有关图形的面积2．涉及三角形的面积型当一次函数与反比例函数结合时，可通过面积作和或作差的形式来求解．（1）正比例函数与一次函数所围成的三角形面积.如图①，S △ABC =2S △ACO =|k |；（2）如图②，已知一次函数与反比例函数y =k x 交于A 、B 两点，且一次函数与x 轴交于点C ，则S △AOB =S △AOC +S △BOC =12OC ⋅|y A |+12OC ⋅|y B |=12OC ⋅(|y A |+|y B |)；（3）如图③，已知反比例函数y =k x 的图象上的两点，其坐标分别为(x A ，y A )，(x B ，y B )，C 为AB 延长线与x 轴的交点，则S △AOB =S △AOC –S △BOC =12OC ⋅|y A |–12OC ⋅|y B |=12OC ⋅(|y A |―|y B |)． 【典例分析】题型1：一点在反比例函数图象上【例1】如图，反比例函数y =k x (k ≠0)的图象上有一点A ，AB 平行于x 轴交y 轴于点B ，△ABO 的面积是3，则反比例函数的解析式是( )A. y =32xB. y =3xC. y =6xD. y =34x【答案】C【解析】解：如图，过点A作AC⊥x轴于点C.则四边形ABOC是矩形，∴S△ABO=S△AOC=3，∴|k|=S矩形ABCO=S△ABO+S△AOC=6，∴k=6或k=―6．又∵函数图象位于第一象限，∴k>0，∴k=6.则反比函数解析式为y=6．x故答案为：C.【练1】如图，P是反比例函数图象在第二象限上的一点，矩形PEOF的面积为5，则反比例函数的表达式是________．【答案】y=―5x(k≠0)，【解析】解：设反比例函数的表达式是y=kx由题意知，S矩形PEOF=|k|=5，所以k=±5，又反比例函数图象在第二象限上，k<0，所以k=―5，即反比例函数的表达式是y=―5．x（x＞0）的图象上，过点A作AD⊥y轴于点D，延长AD至点C，【练2】如图，点A在反比例函数y=kx使AD＝DC，过点A作AB⊥x轴于点B，连接BC交y轴于点E．若△ABC的面积为6，则k的值为 ．【答案】6【解析】解：连接BD ，如图，∵AD ＝DC ，∴S △ADB ＝S △BDC =12S △BAC =12×6＝3，∵AD ⊥y 轴于点D ，AB ⊥x 轴，∴四边形OBAD 为矩形，∴S 矩形OBAD ＝2S △ADB ＝2×3＝6，∴k ＝6．故答案为：6．【练3】如图，在平面直角坐标系xOy 中，反比例函数y =―8x 在第二象限的图象上有一点A ，过点A 作AB ⊥x 轴于点B ，则S △AOB ＝ ．【答案】4【解析】解：设点A 的坐标为（a ，―8a ），∵反比例函数y =―4x 在第二象限的图象上有一点A ，过点A 作AB ⊥x 轴于点B ，∴S △AOB =a⋅(8a )2=4，故答案为：4．题型2：两点在反比例函数图象上【例2】如图，双曲线y=kx与△OAB交于点A，C，已知A，B，C三点横坐标的比为5：5：2，且S△OAB＝21，则k＝ ．【答案】8【解析】解：如图，过点A作AE⊥x轴于点E，过点C作CD⊥x轴于点D，∵A，B，C三点横坐标的比为5：5：2，∴设A、B的横坐标为5a，则C点的横坐标为2a，∵S△OAB＝21，∴12AB⋅5a=21，∴AB=42 5a，∵双曲线y=kx与△OAB交于点A，C，∴CD=k2a，AE=k5a，OD＝2a，OE＝5a，∴BE=k42 5a，∵CD∥BE，∴△OCD∽△OBE，∴CDBE=ODOE，k5a 2a 5a，解得，k＝8，故答案为：8．【练1】如图，矩形ABCD的顶点A和对称中心在反比例函数y=kx（k≠0，x＞0）的图象上，若矩形ABCD 的面积为12，则k的值为（ ）A．6B．C．D．12【答案】A【解析】设A（m，km），∴AB=km，∵矩形的面积为12，∴BC=12km=12mk，∴矩形对称中心的坐标为：（m+12×12mk，12×km），即（m+6mk，k2m）∵对称中心在y=kx的图象上，∴k2m =km6mk，∴mk﹣6m＝0，∴m（k﹣6）＝0，∴m＝0（不符合题意，舍去）或k＝6，故选：A．【练2】如图，点A、B在反比例函数y=kx的图象上，过点A、B作x轴的垂线，垂足分别是M、N，射线AB交x轴于点C，若OM＝MN＝NC，四边形AMNB的面积是3，则k的值为（ ）A．-2B．-4C．2D．4【答案】B【解析】解：∵点A、B在反比例函数y的图象上，∴S△AOM=12|k|，∵OM＝MN＝NC，∴AM＝2BN，∴S△AOM=13S△AOC，S△ACM＝4S△BCN，S△ACM＝2S△AOM，∵四边形AMNB的面积是3，∴S△BCN＝1，∴S△AOM＝2，∴|k|＝4，∵反比例函数y=kx的图象在第二四象限，∴k＝﹣4，故答案为：B．【练3】如图，在平面直角坐标系中，矩形ABCO的两边OA，OC落在坐标轴上，反比例函数y=kx的图象分别交BC，OB于点D，点E，且BDCD =54，若S△AOE＝24，则k的值为 ．【答案】-16【解析】解：设点B的坐标为（a，b），则点D的坐标为（kb，b），点A的坐标为（a，0），∴BD=kb ―a，BC＝﹣a，CD=―kb，AB＝b，∵BDCD =54，∴4×（kb ―a）＝5×（―kb），∴ab=94k，设点E坐标为（m，n），∵S △AOE ＝12，即―12an ＝12，∴n =―24a，∵点E 在反比例函数y =k x 上，∴E （―ak 24，―24a），∵S △AOE ＝S 矩形OABC ﹣S △OBC ﹣S △ABE ＝﹣ab ―12（﹣ab ）―12b （―ak 24―a ）＝12，∴abk ＝576，把abk ＝576代入ab =94k 得，94k 2＝576，即k 2＝162，解得k ＝±16，由图象可知，k ＜0，∴k ＝﹣16．故答案为：-16【练4※】如图，过原点的直线与反比例函数y =k x (k >0)的图象交于A ，B 两点，点A 在第一象限点C 在x 轴正半轴上，连结AC 交反比例函数图象于点D .AE 为∠BAC 的平分线，过点B 作AE 的垂线，垂足为E ，连结DE .若AC =3DC ，ΔADE 的面积为8，则k 的值为________.【答案】6【解析】解：连接OE ，CE ，过点A 作AF ⊥x 轴，过点D 作DH ⊥x 轴，过点D 作DG ⊥AF ，∵过原点的直线与反比例函数y=k x （k ＞0）的图象交于A ，B 两点，∴A 与B 关于原点对称，∴O 是AB 的中点，∵BE ⊥AE ，∴OE=OA ，∴∠OAE=∠AEO ，∵AE 为∠BAC 的平分线，∴∠DAE=∠AEO ，∴AD ∥OE ，∴S △ACE =S △AOC ，∵AC=3DC ，△ADE 的面积为8，∴S △ACE =S △AOC =12，设点A （m ，k m ），∵AC=3DC ，DH ∥AF ，∴3DH=AF ，∴D （3m ，k 3m ），∵CH ∥GD ，AG ∥DH ，∴△DHC ∽△AGD ，∴S △HDC =14S △ADG ，∵S △AOC =S △AOF +S 梯形AFHD +S △HDC=12k +12×(DH +AF)×FH +S ΔHDC=12k +12×4k 3m ×2m +12×14×2k 3m ×2m=12k +4k 3+k 6=12，∴2k=12，∴k=6；故答案为：6.【例4】如图，在平面直角坐标系中，△OAB 的顶点A 在x 轴正半轴上，OC 是△OAB 的中线，点B 、C 在反比例函数y =2x （x ＞0）的图象上，则△OAB 的面积等于 ．【答案】3【解答】解：如图，过点B 、点C 作x 轴的垂线，垂足为D ，E ，则BD ∥CE ，∴CE BD =AE AD =AC AB ，∵OC 是△OAB 的中线，∴CE BD =AE AD =AC AB =12，设CE ＝m ，则BD ＝2m ，∴C 的横坐标为 2m ，B 的横坐标为1m ，∴OD =1m ，OE =2m ，∴DE ＝OE ﹣OD =1m ，∴AE ＝DE =1m ，∴OA ＝OE +AE =3m ，∴S △OAB =12OA •BD =12×3m ×2m ＝3．故答案为：3．【练1】如图，Rt △AOB 的一条直角边OB 在x 轴上，双曲线y =k x (x ＞0)经过斜边OA 的中点C ，与另一直角边交于点D ．若S △OCD ＝9，则S △OBD 的值为 ．【答案】6【解析】解：如图，过C点作CE⊥x轴，垂足为E．∵Rt△OAB中，∠OBA＝90°，∴CE∥AB，∵C为Rt△OAB斜边OA的中点C，∴CE为Rt△OAB的中位线，∵△OEC∽△OBA，∴OCOA =12．∵双曲线的解析式是y=kx，即xy＝k∴S△BOD＝S△COE=12|k|，∴S△AOB＝4S△COE＝2|k|，由S△AOB﹣S△BOD＝S△AOD＝2S△DOC＝18，得2k―12k＝18，k＝12，S△BOD＝S△COE=12k＝6，故答案为：6．【练2】在平面直角坐标系中，对于不在坐标轴上的任意一点A(x,y)，我们把点A的“倒数点”．如图，矩形OCDE的顶点C为(3,0)，顶点E在y轴上，函数y=2x(x>0)的图象与DE交于点A．若点B是点A 的“倒数点”，且点B 在矩形OCDE 的一边上，则△OBC 的面积为_________．【答案】14或32【解析】解：根据题意，∵点A (x,y )的“倒数点”，∴x ≠0，y ≠0，∴点B 不可能在坐标轴上；∵点A 在函数y =2x (x >0)的图像上，设点A 为(x,2x )，则点B 为(1x ,x 2)，∵点C 为(3,0)，∴OC =3，①当点B 在边DE 上时；点A 与点B 都在边DE 上，∴点A 与点B 的纵坐标相同，即2x =x 2，解得：x=2，经检验，x=2是原分式方程的解；∴点B 为（12，1），∴△OBC 的面积为：S =12×3×1=32；②当点B 在边CD 上时；点B 与点C 的横坐标相同，∴1x =3，解得：x =13，经检验，x =13是原分式方程的解；∴点B 为(3,16)，∴△OBC 的面积为：S =12×3×16=14；故答案为：14或32．题型3：两个反比例函数综合问题【例5※】如图，经过原点O 的直线与反比例函数y ＝a x （a ＞0）的图象交于A ，D 两点（点A 在第一象限），点B ，C ，E 在反比例函数y ＝b x （b ＜0）的图象上，AB ∥y 轴，AE ∥CD ∥x 轴，五边形ABCDE 的面积为56，四边形ABCD 的面积为32，则a ﹣b 的值为__，b a 的值为__．【答案】24；﹣13【解析】解：如图，连接AC ，OE ，OC ，OB ，延长AB 交DC 的延长线于T ，设AB 交x 轴于K ．由题意A ，D 关于原点对称，∴A ，D 的纵坐标的绝对值相等，∵AE ∥CD ，∴E ，C 的纵坐标的绝对值相等，∵E ，C 在反比例函数y ＝b x 的图象上，∴E ，C 关于原点对称，∴E ，O ，C 共线，∵OE ＝OC ，OA ＝OD ，∴四边形ACDE 是平行四边形，∴S △ADE ＝S △ADC ＝S 五边形ABCDE ﹣S 四边形ABCD ＝56﹣32＝24，∴S △AOE ＝S △DEO ＝12，∴12a ﹣12b ＝12，∴a ﹣b ＝24，∵S △AOC ＝S △AOB ＝12，∴BC ∥AD ，∴BC AD ＝TB TA ，∵S △ACB ＝32﹣24＝8，∴S △ADC ：S △ABC ＝24：8＝1：3，∴BC ：AD ＝1：3，∴TB ：TA ＝1：3，设BT ＝a ，则AT ＝3a ，AK ＝TK ＝1.5k ，BK ＝0.5k ，∴AK ：BK ＝3：1，∴S △AOK S △BKO ＝1212a b -＝13，∴a b ＝﹣13．故答案为24，﹣13．【练1】如图，直线l ⊥x 轴于点P ，且与反比例函数y 1=k 1x （x ＞0）及y 2=k 2x （x ＞0）的图象分别交于点A ，B ，连接OA ，OB ，已知△OAB 的面积为3，则k 1﹣k 2＝ ．【答案】6【解析】解：∵反比例函数y 1=k 1x （x ＞0）及y 2=k 2x （x ＞0）的图象均在第一象限内，∴k 1＞0，k 2＞0．∵AP ⊥x轴，∴S △OAP =12k 1，S △OBP =12k 2．∴S △OAB ＝S △OAP ﹣S △OBP =12（k 1﹣k 2）＝3，解得：k 1﹣k 2＝6．故答案为：6【练2】双曲线C 1：y =k 1x 和C 2：y =k 2x 如图所示，点A 是C 1上一点，分别过点A 作AB ⊥x 轴，AC ⊥y 轴，垂足分别为点B 、点C ，AB ，AC 与C 2分别交于点D 、点E ，若四边形ADOE 的面积为4，则k 1﹣k 2＝ ．【答案】-4【解析】解：∵D ，E 在反比例函数y =k 2x 的图象上，且图象在第二象限，∴S △OBD =12OB •BD =―12k 2，S △OCE =12OC •CE =―12k 2，∵A 在反比例函数y =k 1x 的图象上，且图象在第二象限，∴S 矩形ABOC ＝OB •OC ＝﹣k 1∴k 1﹣k 2＝﹣[﹣k 1﹣（﹣k 2）]＝﹣（S 矩形ABOC ﹣S △OBD ﹣S △OCE ）＝﹣S 四边形ADOE ＝﹣4，故答案为：﹣4．【练3】如图，点A 是第一象限内双曲线y =m x （m ＞0）上一点，过点A 作AB ∥x 轴，交双曲线y =n x （n ＜0）于点B ，作AC ∥y 轴，交双曲线y =n x （n ＜0）于点C ，连接BC ．若△ABC 的面积为92，则m ，n 的值不可能是（ ）A ．m =19，n =―109B ．m =14，n =―54C ．m ＝1，n ＝﹣2D ．m ＝4，n ＝﹣2【答案】A【解析】解：设点A 的坐标为（a ，m a ），∵AB ∥x 轴，AC ∥y 轴，∴点B 的纵坐标为m a ，点C 的横坐标为a ，将y =m a 代入反比例函数y =n x 得，x =an m ，∴B （an m ，m a ），∴AB ＝a ―an m ，将x ＝a 代入反比例函数y =n x 得，y =n a ，∴C （a ，n a ），∴AC =m n a ，∵S △ABC =12AB •AC =12（a ―an m ）×m n a =(m n )22m =92，即（m ﹣n ）2＝9m ，当m =19，n =―109时，不满足（m ﹣n ）2＝9m ，因此选项A 符合题意；当m =14，n =―54时，当m ＝1，n ＝﹣2时，当m ＝4，n ＝﹣2时，均满足（m ﹣n ）2＝9m ，因此选项B 、C 、D 均不符合题意；故选：A ．。

1.k的几何意义如图，过双曲线上任一点P作x轴、y轴的垂线PM、PN,所得矩形PMON的面积S=|xy|= |k|.由此就建立起了几何图形的面积与k的关系。

2.与k相关的面积问题的基本图形理解并记住这几个基本图形中阴影部分的面积与|k|的关系会对我们解决与反比例函数的面积有关的问题带来非常大的帮助。

反比例函数中与k相关的面积的问题，其本质是过双曲线上的点向坐标轴作垂线，建立起双曲线上的点与图形面积之间的关系。

当图形中的线段有倍分的关系时，通常设未知数，结合中点坐标公式或相似三角形的性质来示解。

例1.在反比例函数4yx的图像中，阴影部分的面积不等于4的是 ( )A B C DyxOyxOyxOyxO【答案】B例2.如图， Rt AOB V 的一条直角边OB 在x 轴上，双曲线(0)ky k x=>经过斜边OA 中点C ，与另一直角边交于点D ，若9OCD S =V ，则k 的值为__________．【答案】12例 3.如图，在平面直角坐标系中， Rt ABO ∆的顶点O 与原点重合，顶点B 在x 轴上， 90ABO ∠=︒,OA 与反比例函数()0ky k x=≠的图像交于点D ，且2OD AD =，过点D 作x 轴的垂线交x 轴于点C .若ABCD S 四边形=10，则k 的值为___________【答案】-161.如图所示，直线l 与双曲线ky x =（k ＞0）交于A ，B 两点，点P 在线段AB 上，试比较△AOC 的面积1S ，△BOD 的面积2S ，△POE 的面积3S 的大小关系。

答案】1S =2S =3S【解析】由基本图形可知，1S =12|k |，2S =12|k |，3S =12|k |， 所以1S =2S =3S 学科@网2.如图，矩形ABCD 的边分别与两坐标轴平行，对角线AC 经过坐标原点，点D 在反比例函数y=kx（x ＞0）的图象上．若点B 的坐标为（﹣2，﹣2），则k=_____．【答案】43.如图，反比例函数()0ky x x=>的图像交Rt OAB ∆的斜边OA 于点D ,交直角边AB 于点C ,点B 在x 轴上，若OAC ∆的面积为5，:1:2AD OD =，则k 的值为【答案】4【解析】过点D 作x 轴的垂线，垂足为点E ，设点A （3m ，3n ），1．如图所示，在平面直角坐标系中，矩形ABCD的BC边落在y轴上，其它部分均在第一象限，双曲线y=k x过点A，延长对角线CA交x轴于点E，以AD、AE为边作平行四边形AEFD，若平行四边形AEFD的面积为4，则k值为（）A. 2B. 4C. 8D. 12【答案】B【解析】延长CD，EF交于H，延长DA交x轴于G，延长AB交EF于N，则△DHF≌△AGE≌△AEN，∴S四边形ABOE=S四边形ADHE，∴S四边形ABOG=S四边形AEFD=4，∵双曲线y=kx过点A，∴k=4．学科@网2．如图，Rt△OAB的边OA在x轴上，点B在第一象限，点D是斜边OB的中点，反比例函数kyx经过点D，若S△AOD=6，则k=________.【答案】6∵∴，即∵点D在kyx=上，∴kba=即∴k=6.学科@网3．如图所示，反比例函数y=kx（k≠0，x＞0）的图象经过矩形OABC的对角线AC的中点D．若矩形OABC的面积为8，则k的值为_______．【答案】24．如图，已知第一象限内的点A在反比例函数2yx=上，第二象限的点B在反比例函数kyx=上，且OA⊥OB，sinA＝3，则k的值为________．【答案】-15.反比例函数6yx=与3yx=在第一象限的图象如图所示，作一条平行于x轴的直线，分别交双曲线于A，B两点，连接OA，OB，求△AOB的面积。

反比例函数k 的几何意义全文共四篇示例，供读者参考第一篇示例：反比例函数是一种常见的函数形式，它在数学中起着重要的作用。

在数学中，反比例函数通常表示为y = k/x，其中k是一个常数。

在本文中，我们将探讨反比例函数k的几何意义，以便更好地理解它在数学中的应用。

让我们来看看反比例函数y = k/x的图像是什么样子的。

当k大于0时，函数图像呈现出一种特殊的形状，即一条从第一象限经过原点的曲线。

这种曲线被称为双曲线。

双曲线在数学中有着广泛的应用，例如在物理学和工程学中，它往往用来描述两个量之间呈反比例关系的情况。

在几何意义上，反比例函数k的值可以理解为曲线在坐标系中的形态和性质。

当k越大时，曲线越扁平，即曲线的曲率越小。

反之，当k 越小时，曲线越尖锐，曲率越大。

反比例函数k的值可以用来描述曲线的形状和性质。

反比例函数k的几何意义还可以从另一个角度来理解。

在数学中，函数y = k/x表示了两个变量之间的反比例关系。

当x增大时，y的值会减小。

这表明两个变量之间存在一种相反变化的关系。

在几何上，这种反比例关系可以理解为一种“交换”的关系，即当一个变量增大时，另一个变量会减小，反之亦然。

反比例函数k在数学中具有重要的几何意义。

它不仅可以描述曲线的形状和性质，还可以揭示两个变量之间的反比例关系。

通过深入研究反比例函数k的几何意义，我们可以更好地理解它在数学中的应用，并丰富我们对数学的认识和理解。

【文章字数不足，如有需要可继续添加内容】。

第二篇示例：反比例函数是数学中常见的一类函数，其数学表达式为y = k/x，其中k为一个常数且k≠0。

反比例函数在数学中有很多重要的应用，尤其是在几何中具有重要的意义。

我们来看反比例函数在几何中的基本性质。

对于反比例函数y =k/x，我们可以通过绘制其图像来直观地理解其性质。

当x取正值时，y 的值随着x的增大而减小；当x取负值时，y的值随着x的增大而增加。

这说明反比例函数是一个非对称的函数，它在坐标系中的图像呈现出一种特殊的形态。

一次函数，反比例函数k的几何意义
一次函数和反比例函数是数学中常见的函数形式，它们在几何
上有着重要的意义。

通过对这两种函数的几何意义进行深入的探讨，我们可以更好地理解它们在实际生活和数学问题中的应用。

一次函数的一般形式为y = mx + c，其中m和c为常数，m表
示直线的斜率，c表示截距。

从几何意义上来看，一次函数代表了
一条直线，斜率m表示了直线的倾斜程度，截距c表示了直线与y
轴的交点位置。

通过改变m和c的值，我们可以得到不同斜率和截
距的直线，从而描绘出各种不同的直线图像。

反比例函数的一般形式为y = k/x，其中k为常数。

从几何意
义上来看，反比例函数代表了一种双曲线的图像。

当x取不同的值时，y的取值会随之变化，从而描绘出双曲线的形状。

反比例函数
在实际生活中有着广泛的应用，比如物理学中的牛顿万有引力定律
和库仑定律，经济学中的供求关系等都可以用反比例函数来描述。

在几何意义上，反比例函数k表示了双曲线的开口大小和位置。

当k的值越大时，双曲线的开口越小，反之亦然。

通过改变k的值，我们可以得到不同形状和大小的双曲线，从而更好地理解反比例函
数在几何上的意义。

总之，一次函数和反比例函数在几何上有着重要的意义，通过对它们的几何意义进行深入的探讨，我们可以更好地理解它们在数学和实际生活中的应用。

希望本文能够帮助读者更好地理解一次函数和反比例函数在几何上的意义。