反比例函数k的几何意义

反比例函数中k的几何意义的应用
k在反比例函数中具有重要的几何意义，以下列举一些它的应用。

1. 直线反比例函数：k反映直线斜率的倒数，即斜率m=-k。

当给定直
线k值时，由定点和k值可以求出斜率m，从而可以绘制出这条直线。

2. 圆反比例函数：k反映圆半径r的倒数，即r=1/k。

当给定圆k值时，由定点和k值可以求出圆半径，从而可以绘制出这个圆。

3. 抛物线反比例函数：k反映抛物线的开口方向，当k > 0时，抛物线
向右开口；当k < 0时，抛物线向左开口。

4. 双曲线反比例函数：k反映双曲线的开口方向，当k＞0时，双曲线
开口向右；当k＜0时，双曲线开口向左。

5. 其他函数反比例函数：k可以反映此类函数中曲线的凹凸，当k > 0时，曲线是凹曲线；当k < 0时，曲线是凸曲线。

总之，k在反比例函数中应用广泛，几乎所有的函数都可以用反比例函
数表示。

它的几何意义非常重要，不仅仅可以根据k值绘制出各种曲线，而且可以了解曲线的开口方向以及凹凸方向。

因此，k在反比例函
数绘制中发挥着重要的作用。

《反比例函数K的几何意义》教学设计教学目标：1.了解反比例函数的定义及其特点。

2.掌握反比例函数的图像特征和变化规律。

3.理解反比例函数中k的几何意义。

教学重点：1.反比例函数的定义及其特点。

2.反比例函数中k的几何意义。

教学难点：理解反比例函数中k的几何意义。

教学准备：黑板、粉笔、绘图工具、反比例函数相关练习题。

教学过程：Step 1：导入新知1.引入：假设有一个正比例函数y=k/x，其中k为常数，x和y均为实数。

请回顾一下正比例函数的性质以及与直线的关系。

2.提问：那么，如果我们把正比例函数中的比例系数k变成k/x，会有什么不同的效果吗？3.要求学生独立思考并回答问题。

1.反比例函数的定义：反比例函数是指函数y=k/x，其中x≠0，k为常数，x和y均为实数。

2.特点：a.当x>0时，y随着x的增大而减小，与正比例函数相反。

b.当x<0时，y随着x的减小而减小，同样与正比例函数相反。

c.当x=0时，反比例函数无定义。

Step 3：反比例函数图像的绘制1.根据反比例函数的定义和特点，先选择几个不同的k的值，绘制出对应的反比例函数图像。

2.强调图像的特点：从x=1开始，k越大，图像越趋近于y轴；k越小，图像越平缓。

Step 4：反比例函数中k的几何意义1.提问：根据反比例函数的图像特点，我们发现k的大小对图像有何影响？2.学生回答：k的大小决定了反比例函数图像的陡峭程度。

3.引导思考：反比例函数中的k是什么意思？有什么几何意义？4.给出答案：在反比例函数图像上，k即为x轴上的一点的坐标。

5.教师解释：图像上在y轴上的其中一点的横坐标就是k，因此k表示了这个反比例函数相关的两个变量之间的比例关系。

1.教师出示几道反比例函数的相关练习题，要求学生独立完成并讨论。

2.部分学生上台解答题目，其他学生进行评价和讨论。

Step 6：归纳总结1.教师总结：反比例函数是由y=k/x的形式表示的函数，其中k是函数的比例系数，决定了函数图像的特点。

反比例函数中K的几何意义
在反比例函数中，K表示比例系数或常数，也被称为反比例常数。

它
是用来确定两个变量之间反比关系的重要参数。

反比例函数的一般形式为：y=K/x，其中K表示比例系数。

K的几何意义可以通过分析反比例函数的图像得出。

反比例函数的图
像是一个双曲线，特点是曲线趋向于两个坐标轴。

下面将详细讨论K的几
何意义。

1.K的符号对于曲线的位置以及开口方向具有重要影响。

如果K为正数，那么曲线将位于第一和第三象限，并且开口方向为右上和左下。

如果
K为负数，那么曲线将位于第二和第四象限，并且开口方向为左上和右下。

2.K的绝对值越大，曲线就越“陡峭”。

当K增大时，曲线将更加接
近于坐标轴，并且在原点附近的斜率会越来越大。

反之，当K变小时，曲
线将更加平缓，斜率将减小。

3.K决定了特定坐标点的函数值。

例如，在函数y=K/x中，当x为K 时，y的值将为1、这是因为x与y成反比关系，而K是这种关系的常数。

4.K还决定了曲线相对于坐标轴的位置。

具体而言，当K增大时，曲
线将向坐标轴移动，而当K减小时，曲线将远离坐标轴。

总之，K代表了反比例函数中的比例系数或常数，它对于函数的位置、开口方向、陡峭程度以及特定坐标点的函数值都具有重要影响。

通过对K
的分析，我们可以更好地理解和解释反比例函数的几何特征。

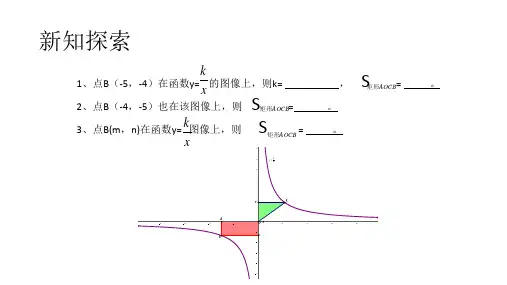
知识讲解1.反比例函数的概念如图所示，过双曲线)0(k≠=kxy上任一点),(yxP作x轴、y轴的垂线PM、PN,垂足为M、N，所得矩形PMON的面积S=PM∙PN=|y|∙|x|.,yxk=∴||kSkxy==，。

这就说明，过双曲线上任意一点作x轴、y轴的垂线，所得到的矩形的面积为常数|k|。

这是系数k几何意义,明确了k的几何意义，会给解题带来许多方便。

（请学生思考，图中三角形OEF的面积和系数k的关系。

）2.反比例函数的图象在用描点法画反比例函数y=kx的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.例题1函数y=1x-(x>0)的图象大致是( )例题2 函数y=kx+1与函数y=kx在同一坐标系中的大致图象是( )yOxAyO xByOxCyOxD y y y y3.反比例函数y=kx 中k 的意义注意:反比例函数y=k x (k ≠0)中比例系数k 的几何意义,即过双曲线y=kx(k ≠0)上任意一点引x 轴、y 轴垂线,所得矩形面积为│k │.例题1：如图，P 、C 是函数x4y =（x>0）图像上的任意两点，过点P 作x 轴的垂线PA,垂足为A ，过点C 作x 轴的垂线CD,垂足为D ，连接OC 交PA 于点E ，设⊿POA 的面积为S1,则S1= ,梯形CEAD 的面积为S2，则S1与S2的大小关系是S1 S2, ⊿POE 的面积S3和梯形CEAD 的面积为S2的大小关系是S2 S3.例题1图 例题2图 例题3图例题2：如图所示，直线l 与双曲线)0(ky >=k x交A 、B 两点，P 是AB 上的点，试比较⊿AOC 的面积S1，⊿BOD 的面积S2，⊿POE 的面积S3的大小： 。

例题3：如图所示，点A(x1,y1)、B(x2,y2)都在双曲线)0x (k>=xy 上,且x2-x1=4,y1-y2=2;分别过点A 、B 向x 轴、y 轴作垂线，垂足分别为C 、D 、E 、F ，AC 与BF 相交于G 点，四边形FOCG 的面积为2，五边形AEODB 的面积为14，那么双曲线的解析式为 。

反比例函数的K的几何意义教学设计教学目标：1.通过探究和解决实际问题，学生能够理解反比例函数y=k/x的策略。

2.学生能够准确描述反比例函数的K的几何意义。

3.学生能够运用反比例函数的K的几何意义解决实际问题。

4.培养学生的观察能力和解决问题的能力。

教学准备：1.班级投影仪和教师电脑。

2.反比例函数PPT和演示文稿。

3.黑板和白板笔。

4.一些实际问题的案例。

教学过程：Step 1：引入概念（10分钟）1.教师在黑板上解释反比例函数的定义y=k/x，并强调k的作用。

2.教师可以通过简单的实例解释k的意义，例如：y=2/x，当x=1时，y=2；当x=2时，y=1等。

Step 2：几何意义的探索（30分钟）1.教师引导学生思考反比例函数y=k/x的几何意义。

学生可以绘制函数图像，并观察变化。

2.教师提出问题：“当k为正数时，函数图像是什么样子？当k为负数时，函数图像是什么样子？”学生可以通过探索和实例验证答案。

3.教师引导学生找到反比例函数图像上的特殊点，例如：x=0，y=k。

教师解释这个特殊点的意义，即当x无限大或无限小时，y趋近于0，表示k对应的y值是反比例函数的一个特殊点。

Step 3：实际问题的应用（40分钟）1.教师提供一些实际问题的案例，例如：速度与时间的关系、工人的工作效率与工作时间的关系等。

2.学生利用所学的反比例函数的知识，运用k的几何意义，解决这些实际问题。

3.学生分组讨论解决实际问题的方法，并在小组内互相交流思路和解答结果。

4.学生进行小组报告，分享他们的解决方法和思考过程。

Step 4：课堂总结（10分钟）1.教师总结本节课的内容，强调反比例函数k的几何意义的重要性。

2.教师激发学生对数学的兴趣，鼓励学生在日常生活中运用反比例函数的知识解决实际问题。

Step 5：课后延伸（选）1.学生利用k的几何意义，设计其他实际问题的解决方案。

2.学生参加数学竞赛或编写数学问题册子，提出反比例函数相关的问题。

反比例函数的K的几何意义教学设计教学设计：反比例函数的K的几何意义一、教学目标：1.了解反比例函数的特点和性质；2.理解反比例函数中K的几何意义；3.通过几何图形展示反比例函数中K的变化对图像的影响；4.能够根据K的取值判断反比例函数是否为增函数或减函数。

二、教学准备：白板、白板笔、幻灯片、投影仪。

三、教学过程设计：1.导入（10分钟）教师先出示一张幻灯片，上面写有反比例函数的定义和性质，并向学生解释反比例函数的概念和特点，引发学生对反比例函数的兴趣。

然后，教师可以问学生：反比例函数的图像有什么特点？学生可以提出自己的看法。

2.探究（30分钟）让学生自己动手，通过具体的例子来研究反比例函数中K的几何意义。

教师提供几个反比例函数的实例，比如y=k/x，其中K=1，K=2，K=3等等。

然后，让学生根据这些K的值，画出对应的函数图像。

注：在探究过程中，教师可以引导学生思考并回答以下问题：1）当K=1时，图像是什么样的？2）当K>1时，图像是什么样的？3）当K<1时，图像是什么样的？4）当K=0时，图像是什么样的？学生可以通过观察图像的变化，总结出K值与图像的关系。

3.总结（10分钟）教师引导学生讨论，并总结K在反比例函数中的几何意义：1）当K>1时，图像呈现出下降的趋势，K表示图像的陡峭程度；2）当K<1时，图像呈现出上升的趋势，K表示图像的平缓程度；3）当K=0时，图像是一条水平线；4）当K<0时，图像是不连续的。

4.巩固与拓展（30分钟）让学生根据已有的知识，自己解决以下问题：1）反比例函数y=k/x在横轴和纵轴之间是否有一个因果关系？如果有，请给出一个具体的例子说明；2）反比例函数y=k/x中，当K>0时，函数的图像是什么样的？当K<0时，函数的图像又是什么样的？3）反比例函数y=k/x中，当K=1时，函数是否为增函数？当K<1时，函数是否为减函数？学生可以自行思考并回答这些问题。