第四章 静电场中的导体

静电场中的导体2.1 填空题2.1.1 一带正电小球移近不带电导体时，小球将受到（ ）力作用；一带负电小球移近不带电导体时，小球将受到（ ）力作用；一带正电小球靠近不带电的接地导体时，小球将受到（ ）力作用。

2.1.2 在一个带正电的大导体附近P 点放置一个点电荷q(电荷q 不是足够小)，实际测得它的受力为F ，如果q>0, 则F/q 与P 点场强E 0关系为（ ），如果q<0, 则F/q 与P 点场强关系为( )2.1.3 导体在静电场中达到静电平衡的条件是（ ）和（ ）。

2.1.4 导体处于静电平衡状态时，导体内部电荷体密度（ ），电荷只能分布在（ ）。

2.1.5 导体处于静电平衡状态时，导体是（ ）体，表面是（ ）面。

2.1.6 接地导体的电势等于（ ），地球与（ ）等电势。

2.1.7 一导体球壳，内外半径分别为R 1和R 2，带电q ，球壳内还有一点电荷q ，则导体球壳的电势是（ ）。

2.1.8 一点电荷q 放在一接地的无限大导电平面附近，则导电平面上的总电量为（ ）。

2.1.9 将一个点电荷+q 移近一个不带电的导体B 时，则导体B 的电势将（ ）。

2.1.10 一封闭导体壳C 内有一些分别带q 1、q 2…的带电体，导体壳C 外也有一些分别带Q 1、Q 2…的带电体，则q 1、q 2…的大小对导体壳C 外的电场强度（ ）影响，对C 外的电势（ ）影响；Q 1、Q 2…的大小对导体壳C 内的电场强度（ ）影响，对C 内的电势（ ）影响。

2.1.11 两个同心导体球壳A 、B ，若内球B 上带电q ，则电荷在其表面上的分布呈（ ）分布；当从外边把另一带电体移近这两个同心球时，则内球B 上的分布呈（ ）分布。

2.1.12 两导体球半径分别为r A 和r B ，A 球带电q ，B 球不带电，现用一细导线连接，则分布在两球上的电荷之比Q A ∶Q B （ ）。

2.1.13 在带等量异号电荷的二平行板间的均匀电场中，一个电子由静止自负极板释放，经t 时间抵达相隔d 的正极板，则两极板间的电场为（ ），电子撞击正极板的动能为（ ）。

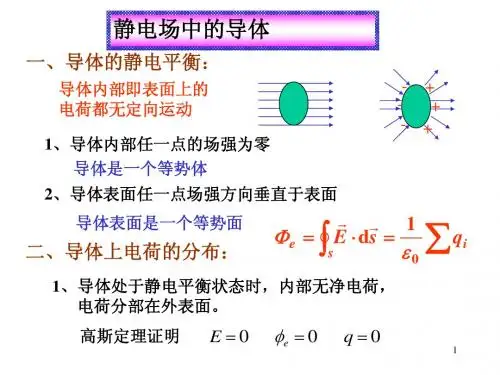
静电场中的导体:
内部场强为零，电势处处相等，导体内部无静电荷！比如外电场迫使正电荷向导体的右端移动，在导体本身中左端是正电荷有端是负电荷，在导体内部又产生了一个电场与外界电场等大反向，所以电荷在导体内部移动不受电场力的作用，所以移动导体不会引起电势能的增加，所以导体内部电势处处相等。

电势到底等于多少，由导体所在点在外电场的电势和内电场电势相加得到，因为电势是标量嘛.
静电场:
静电场，指的是观察者与电荷量不随时间发生变化的电荷相对静止时所观察到的电场。

它是电荷周围空间存在的一种特殊形态的物质，其基本特征是对置于其中的静止电荷有力的作用。

库仑定律描述了这个力。

性质：
根据静电场的高斯定理：
静电场的电场线起于正电荷或无穷远,
终止于负电荷或无穷远，故静电场是有源场．
从安培环路定理来说它是一个无旋场．
根据环量定理，静电场中环量恒等于零,表明静电场中沿任意闭合路径移动电荷，电场力所做的功都为零，因此静电场是保守场．根据库仑定律，两个点电荷之间的作用力跟它们的电荷量的乘积成正比，和它们距离的平方成反比，作用力的方向在它们的连线上，即F=（k·q1q2）/r2;,其中q1、q2为两电荷的电荷量（不计正负性）、
k为静电力常量，约为9.0e+09（牛顿·米2）/（库伦2;），r为两电荷中心点连线的距离。

注意，点电荷是不考虑其尺寸、形状和电荷分布情况的带电体。

是实际带电体的理想化模型。

当带电体的距离比它们的大小大得多时，带电体的形状和大小可以忽略不计的点电荷。

abd =⋅=∫l E U b aab G G证明------------净电荷只能分布于外表面,0;0==内σρ++++++++腔外电荷的电场线不能进入腔内，即：静电屏蔽.+-----+++++00=′+E E G G 思考：静电屏蔽是否意味着腔外电荷不能在腔内产生电场？不是！在腔内：'0=+=E E E G G G 内3）空腔导体，腔内有电荷空腔外表面电荷由电荷守恒决定.−−−−−Sq+紧贴内表面作高斯面S1d 0∑∫==⋅内内qS E sεG G空腔内表面电荷与腔内电荷等值异号.0∑=∴内qq −思考：1）空腔原不带电，腔内电荷，腔内、外表面电量？q 2）空腔原带电.腔内电荷，腔内、外表面电量？q Q +++++++++q q + q −+++++------+++++++++q +q −+++++qQ +++------3）空腔能屏蔽腔内电荷的电场吗？有什么办法能实现这种屏蔽？q qq − 腔接地：内外电场互不影响.+00=′+E E G G -----+++++腔不接地：腔内不受腔外电荷影响腔外要受腔内电荷影响+++++++++q q +q−+++++------4）腔内电荷的位置移动对分布有无影响？q 外内外内，，，E E GG σσq 腔内电荷的位置移动对分布有影响；对分布无影响。

外外，E Gσ，，内内E Gσqq − +++++++++q q +q −+++++------当静电平衡时，导体，净电荷只能分布于表面.?=表σ0=ρ2. 静电平衡时导体表面电荷面密度与表面紧邻处场强成正比.EPG SS 'ΔΔ0=E GS过表面紧邻处作平行于表面的面元,以为底，过法向为轴，作如图高斯面。

P P S ΔS S ΔSS E S E S E S E S E sSS S 'Δ⋅=Δ=⋅+⋅+⋅=⋅∫∫∫∫ΔΔσε01d d d d 侧G G G G G G G G 0=内E Gcos =θG三. 有导体存在时的分布E,U求解思路：3030004 444R q R q r )q (r qU U P B πεπεπεπε=+−+==1R 2R 3R qqq +−Pr A B 0=−=外内B B q q q 〈2〉将B 接地再重新绝缘，结果如何？1R 2R 3R q×q−A B0 ==地接地U U :B B 04 44302010=−+−+=R q q R q R q U '''A πεπεπε由：430≠−==R qU U B A πε〈3〉然后将接地，电荷分布及电势如何变化？A ,B A B A 球电荷入地，B 球壳分布于表面，对吗？q −1R 2R 3R q−AB设带电则'q A, q q q q q 'B 'B −=−=外内1R 2R 3R qq −′q ′q ′−AB与接地条件矛盾，不对！×qR R R R R R qR R q '<+−=21313221即所带部分电荷入地.A 0213132321<+−−=−=R R R R R R qR )R R (q q q 'B 外04421313202130<+−⋅−==)R R R R R R (q)R R (R q U B B πεπε外↓∴B U 1R 2R 3R qq −′q ′q ′−AB[例三]内半径为的导体球壳原来不带电，在腔内离球心距离为处，固定一电量的点电荷，用导线将球壳接地后再撤去地线，求球心处电势.R )R d (d < q +解：〈1〉画出未接地前的电荷分布图.腔内壁非均匀分布的负电荷对外效应等效于：在与同位置处置.q +q −q+d o qq +−R ++++++++--------〈3〉由叠加法求球心处电势.)Rd (q Rq dq U U U q 114 440000−=−+=+=+πεπεπε内壁〈2〉外壳接地后电荷分布如何变化？d o qq +−R ++++++++--------q +q−内壁电荷分布不变0==++==+外壁外壁内壁地壳q U U U U U q [例四]实验表明，在靠近地面处有相当强的电场，电场强度垂直于地面向下，大小约为；在离地面高的地方，也是垂直于地面向下的，大小约为 2 5 N/C .〈1〉试计算从地面到此高度大气中电荷的平均体密度.〈2〉假设地球表面处的电场强度完全是由均匀分布在地表面的电荷产生，求地面上的电荷面密度.km 5.1C /N 100E GE G 解：地球——球对称，离地面不远处( h <<R )——面对称可以用高斯定理求解如何选择高斯面？h2E G 1E G SΔS〈1〉作底面平行于地面，高h =1500 m 的直圆柱为高斯面.由高斯定理∫Δ−Δ=⋅sS E S E S E 12d G G Sh q Δ==∑ρεε011内)(.)(..h )E E (313312120m C 10434 25100105110858−−−⋅×=−×××=−=ερh2E G 1E G SΔS〈2〉作高斯面如图.S S E S E sΔ⋅=Δ−=⋅∫σε021d G G 由高斯定理：)(..E 2101220mC 10858 10010858−−−⋅×−=××−=−=εσ导体上的电荷分布计算分布（方法同前）U E ,G静电平衡条件电荷守恒定律小结：SΔ0=E G导体内σ地面2E G S ΔS练习：若带电带电，求：B ,q A 12q 〈1〉图中1，2，3，4 各区域的和分布，并画出和曲线.U EGr E −r U −〈2〉若将球与球壳用导线连接，情况如何？〈3〉若将外球壳接地，情况如何？BA1R 2R 3R 12 q q 432124021432201214040r q q EEr q EEπεπε+====421043212121023210332121110141 414141r q q U ;)R q q R q r q (U R q q U ;)R q q R q R q (U +=++−=+=++−=πεπεπεπε2111q q q q q q q B B A +=−==外内<1>BA 1R 2R 3R 432111 q q −21q q +rU r E −− , 曲线BA 1R 2R 3R 432111 q q −21q q +rR R R o 321U Er<2>若将球与球壳用导线连接，情况如何？24021432140r q q E EE E πε+====421043021321414r q q U R q q U U U +=+===πεπε21;0q q q q q B B A +===外内BA 1R 2R 3R 12 q q +4321rU r E −− , 曲线BA 1R 2R 3R 12 q q +4321rR R R o 321U Er<3>若将外球壳接地，情况如何？4043220121====E E rq E E πε00)(41)(4143212102211101==−=−=UU R q r q U R q R q U πεπε011=−==外内B B A q q q q q BA1R 2R 3R 432111 - q q rU r E −− , 曲线BA1R 2R 3R 432111 - q qU ErrR R R o 321e+物质结构中存在着正负电荷1.电介质的分类§9.7 静电场中的电介质一. 电介质的极化及其描述+-无极分子•••••cHHHH 无极分子电介质=i p G +-有极分子•••HHo有极分子电介质°1040≠i p G •••••cHHHH 无极分子电介质2.极化现象无外场=i p G 0=∑ii p G +-+-+-+-+-+-外场中(位移极化)≠i p G≠∑ii p G出现束缚电荷和附加电场0E G +-----++++-+E ′G ip G 不一定与表面垂直总00≠′+=E E E GG G •••Ho有极分子电介质°104位移极化和转向极化微观机制不同，宏观效果相同。