2015第6章 控制系统的设计和校正第3讲
- 格式:ppt
- 大小:450.50 KB
- 文档页数:32
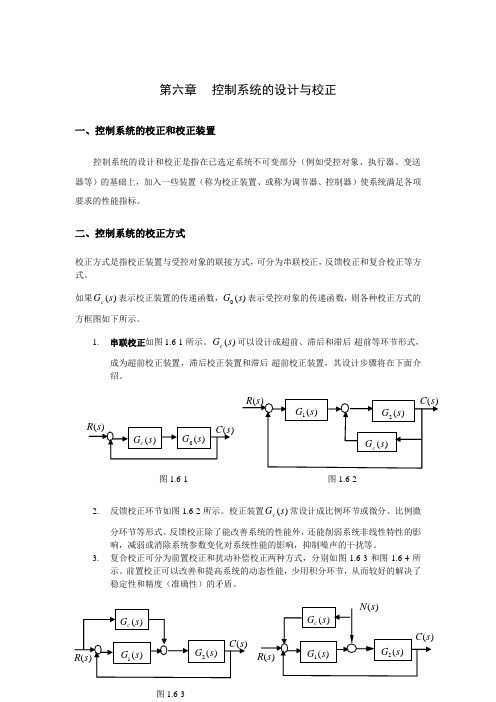
第六章 控制系统的设计与校正一、控制系统的校正和校正装置控制系统的设计和校正是指在已选定系统不可变部分(例如受控对象、执行器、变送器等)的基础上,加入一些装置(称为校正装置、或称为调节器、控制器)使系统满足各项要求的性能指标。
二、控制系统的校正方式校正方式是指校正装置与受控对象的联接方式,可分为串联校正,反馈校正和复合校正等方式。
如果)(s G c 表示校正装置的传递函数,)(0s G 表示受控对象的传递函数,则各种校正方式的方框图如下所示。
1. 串联校正如图1.6-1所示。
)(s G c 可以设计成超前、滞后和滞后-超前等环节形式,成为超前校正装置,滞后校正装置和滞后-超前校正装置,其设计步骤将在下面介绍。
2. 反馈校正环节如图1.6-2所示。
校正装置)(s G c 常设计成比例环节或微分、比例微分环节等形式。
反馈校正除了能改善系统的性能外,还能削弱系统非线性特性的影响,减弱或消除系统参数变化对系统性能的影响,抑制噪声的干扰等。
3. 复合校正可分为前置校正和扰动补偿校正两种方式,分别如图1.6-3和图1.6-4所示。
前置校正可以改善和提高系统的动态性能,少用积分环节,从而较好的解决了稳定性和精度(准确性)的矛盾。
图1.6-1图1.6-211图1.6-3扰动补偿校正目的是为了提高系统的准确度。
通过直接或间接测量出扰动信号,是扰动对系统的影响得到部分或全部的补偿。
图1.6-4的系统又称为前馈-反馈复合控制系统。
在生产过程控制性能要求较高的场合,常采用这种复合控制方式。
三、常用校正装置的特点及优缺点1. 超前校正装置能增加稳定裕量,提高了系统控制的快速性,改善了平稳性。
故适用于稳态精度已满足要求,但动态性能较差的系统。
缺点是会使抗干扰能力下降,改善稳态精度的作用不大。
2. 滞后校正装置能提高系统的稳态精度,也能提高系统的稳定裕量。
故适用于稳态精度要求较高或平稳性要求严格的系统。
缺点是使频带变窄,降低了系统的快速性。


第3讲 机械能守恒定律及其应用 目标要求 1.知道机械能守恒的条件,理解机械能守恒定律的内容.2.会用机械能守恒定律解决单个物体或系统的机械能守恒问题.考点一 机械能守恒的判断1.重力做功与重力势能的关系(1)重力做功的特点①重力做功与________无关,只与始末位置的____________有关.②重力做功不引起物体____________的变化.(2)重力势能①表达式:E p =________.②重力势能的特点重力势能是物体和________所共有的,重力势能的大小与参考平面的选取________,但重力势能的变化与参考平面的选取________.(3)重力做功与重力势能变化的关系重力对物体做正功,重力势能________;重力对物体做负功,重力势能________.即W G =E p1-E p2=-ΔE p .2.弹性势能(1)定义:发生________________的物体的各部分之间,由于有弹力的相互作用而具有的势能.(2)弹力做功与弹性势能变化的关系:弹力做正功,弹性势能________;弹力做负功,弹性势能________.即W =________.3.机械能守恒定律(1)内容:在只有重力或弹力做功的物体系统内,________与________可以互相转化,而总的机械能________________.(2)表达式:mgh 1+12m v 12=___________________________________________________. 1.物体所受的合外力为零,物体的机械能一定守恒.( )2.物体做匀速直线运动,其机械能一定守恒.( )3.物体的速度增大时,其机械能可能减小.()机械能是否守恒的三种判断方法(1)利用机械能的定义判断:若物体动能、势能之和不变,则机械能守恒.(2)利用做功判断:若物体或系统只有重力(或弹簧的弹力)做功,虽受其他力,但其他力不做功(或做功代数和为0),则机械能守恒.(3)利用能量转化判断:若物体或系统与外界没有能量交换,物体或系统内也没有机械能与其他形式能的转化,则机械能守恒.例1忽略空气阻力,下列物体运动过程中满足机械能守恒的是()A.电梯匀速下降B.物体由光滑斜面顶端滑到斜面底端C.物体沿着斜面匀速下滑D.拉着物体沿光滑斜面匀速上升听课记录:_______________________________________________________________________ ________________________________________________________________________________例2一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,下列说法不正确的是()A.运动员到达最低点前重力势能始终减小B.蹦极绳张紧后的下落过程中,弹力做负功,弹性势能增加C.蹦极过程中,运动员、地球和蹦极绳所组成的系统机械能守恒D.蹦极过程中,重力势能的改变量与重力势能零点的选取有关听课记录:_______________________________________________________________________ ________________________________________________________________________________ ________________________________________________________________________________例3如图所示,将一个内外侧均光滑的半圆形槽置于光滑的水平面上,槽的左侧有一固定的竖直墙壁(不与槽粘连).现让一小球自左端槽口A点的正上方由静止开始下落,从A点与半圆形槽相切进入槽内,则下列说法正确的是()A.小球在半圆形槽内运动的全过程中,只有重力对它做功B.小球从A点向半圆形槽的最低点运动的过程中,小球的机械能不守恒C.小球从A点经最低点向右侧最高点运动的过程中,小球与半圆形槽组成的系统机械能守恒D.小球从下落到从右侧离开半圆形槽的过程中,机械能守恒听课记录:_______________________________________________________________________考点二单物体机械能守恒问题1.表达式2.应用机械能守恒定律解题的一般步骤例4(2022·全国乙卷·16)固定于竖直平面内的光滑大圆环上套有一个小环,小环从大圆环顶端P点由静止开始自由下滑,在下滑过程中,小环的速率正比于()A.它滑过的弧长B.它下降的高度C.它到P点的距离D.它与P点的连线扫过的面积听课记录:_______________________________________________________________________ ________________________________________________________________________例5 (2021·浙江1月选考·20改编)如图所示,竖直平面内由倾角α=60°的斜面轨道AB 、半径均为R 的半圆形细圆管轨道BCDE 和16圆周细圆管轨道EFG 构成一游戏装置固定于地面,B 、E 两处轨道平滑连接,轨道所在平面与竖直墙面垂直.轨道出口处G 和圆心O 2的连线,以及O 2、E 、O 1和B 等四点连成的直线与水平线间的夹角均为θ=30°,G 点与竖直墙面的距离d =3R .现将质量为m 的小球从斜面的某高度h 处静止释放.小球只有与竖直墙面间的碰撞可视为弹性碰撞,不计小球大小和所受阻力.(1)若释放处高度h =h 0,当小球第一次运动到圆管最低点C 时,求速度大小v C ;________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________(2)求小球在圆管内与圆心O 1点等高的D 点所受弹力F N 与h 的关系式;________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________(3)若小球释放后能从原路返回到出发点,高度h 应该满足什么条件?________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________________________________________________________________________________考点三系统机械能守恒问题1.解决多物体系统机械能守恒的注意点(1)对多个物体组成的系统,要注意判断物体运动过程中系统的机械能是否守恒.一般情况为:不计空气阻力和一切摩擦,系统的机械能守恒.(2)注意寻找用绳或杆相连接的物体间的速度关系和位移关系.(3)列机械能守恒方程时,一般选用ΔE k=-ΔE p或ΔE A=-ΔE B的形式.2.几种实际情景的分析(1)速率相等情景注意分析各个物体在竖直方向的高度变化.(2)角速度相等情景①杆对物体的作用力并不总是沿杆的方向,杆能对物体做功,单个物体机械能不守恒.②由v=ωr知,v与r成正比.(3)某一方向分速度相等情景(关联速度情景)两物体速度的关联实质:沿绳(或沿杆)方向的分速度大小相等.(4)含弹簧的系统机械能守恒问题①由于弹簧发生形变时会具有弹性势能,系统的总动能将发生变化,若系统除重力、弹簧弹力以外的其他力不做功,系统机械能守恒.②弹簧两端物体把弹簧拉伸至最长(或压缩至最短)时,两端的物体具有相同的速度,弹性势能最大.③对同一弹簧,弹性势能的大小由弹簧的形变量决定,弹簧的伸长量和压缩量相等时,弹簧的弹性势能相等.考向1 速率相等情景例6 如图所示,可视为质点的小球A 、B 用不可伸长的细软轻线连接,跨过固定在地面上、半径为R 的光滑圆柱,A 的质量为B 的两倍.当B 位于地面上时,A 恰与圆柱轴心等高.将A 由静止释放,B 上升的最大高度是( )A .2R B.5R 3 C.4R 3 D.2R 3听课记录:_______________________________________________________________________ ________________________________________________________________________多个物体组成的系统,应用机械能守恒时,先确定系统中哪些能量增加、哪些能量减少,再用ΔE 增=ΔE 减(系统内一部分增加的机械能和另一部分减少的机械能相等)解决问题.考向2 角速度相等情景例7 2023·安徽滁州市定远县第三中学模拟)轮轴机械是中国古代制陶的主要工具.如图所示,轮轴可绕共同轴线O 自由转动,其轮半径R =20 cm ,轴半径r =10 cm ,用轻质绳缠绕在轮和轴上,分别在绳的下端吊起质量为2 kg 、1 kg 的物块P 和Q ,将两物块由静止释放,释放后两物块均做初速度为0的匀加速直线运动,不计轮轴的质量及轴线O 处的摩擦,重力加速度g 取10 m/s 2.在P 从静止下降1.2 m 的过程中,下列说法正确的是( )A .P 、Q 速度大小始终相等B .Q 上升的距离为2.4 mC.P下降1.2 m时Q的速度大小为4 m/sD.P下降1.2 m时的速度大小为4 m/s听课记录:_______________________________________________________________________考向3关联速度情景例8(2023·江苏省苏州八校联盟月考)如图所示,一根轻质弹簧一端固定于光滑竖直杆上,另一端与质量为m的滑块P连接,P穿在杆上,一根轻绳跨过定滑轮将滑块P和重物Q连接起来,重物Q的质量为4m,把滑块从图中A点由静止释放后沿竖直杆上下运动,当它经过A、B两点时弹簧对滑块的弹力大小相等,已知OA与水平面的夹角θ=53°,OB长为3L,与AB垂直,不计滑轮的摩擦,重力加速度为g,sin 53°=0.8,cos 53°=0.6,滑块P从A到B的过程中,下列说法正确的是()A.滑块P的加速度一直减小B.滑块P的最大速度为22gLC.轻绳对滑块P做功为8mgLD.重力对重物Q做功的功率一直减小听课记录:_______________________________________________________________________考向4含弹簧的系统机械能守恒问题例9(2023·江苏省西交大附中高三月考)如图所示,劲度系数为k的轻质弹簧,一端系在竖直放置、半径为R的光滑圆环顶点P处,另一端连接一套在圆环上且质量为m的小球,开始时小球位于A点,此时弹簧处于原长且与竖直方向的夹角为45°,之后小球由静止沿圆环下滑,小球运动到最低点B时速率为v,此时小球与圆环之间的压力恰好为零.下列分析正确的是()A .小球过B 点时,弹簧的弹力大小为m v 2R B .从A 点到B 点的过程中,重力对小球做的功等于小球克服弹簧弹力做的功C .从A 点到B 点的程中,小球的重力势能和弹簧的弹性势能转化为小球的动能D .小球过B 点时,弹簧的弹力大小为(2-2)kR听课记录:_______________________________________________________________________ 例10 如图所示,A 、B 两小球由绕过轻质定滑轮的细线相连,A 放在固定的光滑斜面上,B 、C 两小球在竖直方向上通过劲度系数为k 的轻质弹簧相连,C 球放在水平地面上.现用手控制住A ,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A 的质量为4m ,B 、C 的质量均为m ,重力加速度为g ,细线与滑轮之间的摩擦不计.开始时整个系统处于静止状态;释放A 后,A 沿斜面下滑至速度最大时,C 恰好离开地面.求:(1)斜面的倾角α;(2)A 球获得的最大速度v m 的大小.________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________。


