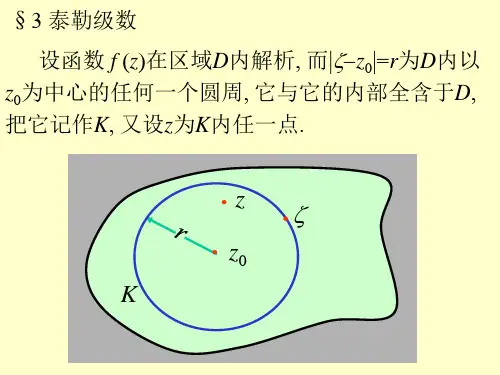
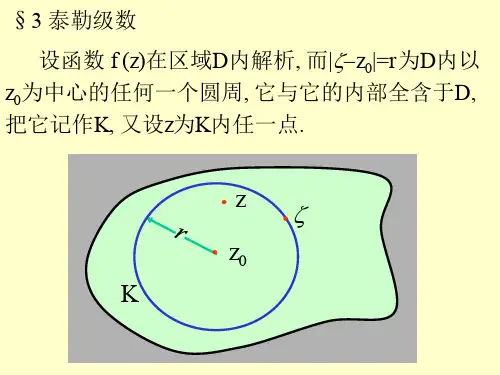
复变函数泰勒定理

复变函数与积分变换泰勒展开式与洛朗展开式复变函数是指复数域上的函数，其自变量和因变量都是复数。

复变函数理论是数学中的一个重要分支，应用广泛。

在物理、工程、经济学以及计算机科学等领域，复变函数都发挥着重要的作用。

复变函数的泰勒展开式和洛朗展开式是两种常见的展开方法，用于将复变函数表示为幂级数或者简单函数的和。

泰勒展开式适用于函数在某个点附近解析的情况，而洛朗展开式适用于函数在某个环域上解析的情况。

泰勒展开式是将函数在某个点处展开成幂级数的形式。

设函数f(z)在z=a处解析，则f(z)可以表示为：f(z) = f(a) + f'(a)(z-a) + f''(a)(z-a)^2 + ...其中，f'(a)表示f(z)在z=a处的导数，f''(a)表示f'(z)在z=a 处的导数，以此类推。

泰勒展开式表明，在某个点处，函数可以用无穷级数的形式表示，通过计算有限项的幂级数，可以近似得到函数在该点附近的值。

洛朗展开式是将函数在某个环域上展开成幂级数和简单函数的形式。

设函数f(z)在环域R: r<|z-a|<R中解析，则f(z)可以表示为：f(z) = ∑ (A_n / (z-a)^n) + ∑ (B_n (z-a)^n)其中，第一项是负幂次项的幂级数，第二项是正幂次项的幂级数，A_n和B_n是系数。

洛朗展开式表明，在某个环域上，函数可以用无穷级数的形式表示，通过计算有限项的幂级数和简单函数的和，可以近似得到函数的值。

泰勒展开式和洛朗展开式对于研究函数的性质和计算函数的值都有重要的指导意义。

通过泰勒展开式和洛朗展开式，我们可以对复变函数进行近似计算，从而简化问题的求解过程。

此外，这两种展开方法也为我们提供了一种描述函数行为的方式，让我们能够更好地理解函数的性质，从而更好地应用于实际问题中。

总之，复变函数的泰勒展开式和洛朗展开式是复变函数理论中重要的工具。

复变函数与积分变换泰勒展开式与洛朗展开式复变函数与积分变换是数学分析中重要的概念和工具。

泰勒展开式和洛朗展开式是这两个概念的应用，可以用来近似计算复变函数和积分变换。

本文将介绍复变函数和积分变换的基本概念，并探讨泰勒展开式和洛朗展开式的原理和应用。

一、复变函数与积分变换1.复变函数复变函数是指定义域和值域都是复数域的函数。

复变函数可以分为两个独立的实部和虚部，即f(z) = u(x, y) + iv(x, y)，其中z = x + iy，u(x, y)和v(x, y)是实函数。

复变函数的基本性质有：（1）全纯性：如果一个复变函数在一些区域内可导，并且导函数连续，则该函数被称为全纯函数。

（2）解析性：如果一个复变函数在一些区域内可导，则该函数称为解析函数。

（3）调和性：如果一个复变函数满足拉普拉斯方程，则该函数称为调和函数。

2.积分变换积分变换是一种数学变换，将函数从一个域变换到另一个域。

积分变换的基本形式为：\[F(s) = \int_{0}^{\infty} f(t)e^{-st} dt\]其中f(t)是定义在正实轴上的函数，F(s)是函数f(t)的积分变换。

常见的积分变换有拉普拉斯变换、傅里叶变换、Z变换等。

这些积分变换在信号处理、控制论、电路分析等领域中得到广泛应用。

1.泰勒展开式泰勒展开式是将一个函数在特定点附近进行无穷阶的展开，近似表达原函数。

泰勒展开式的一般形式为：\[f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 +\frac{f'''(a)}{3!}(x-a)^3 + \cdots\]其中，f(x)是要展开的函数，a是展开点，f'(a)、f''(a)、f'''(a)等表示函数在a点的导数。

对于复变函数f(z)，泰勒展开式的形式为：\[f(z) = f(a) + (z-a)f'(a) + \frac{(z-a)^2}{2!}f''(a) +\frac{(z-a)^3}{3!}f'''(a) + \cdots\]洛朗展开式是将一个函数在复平面上的一定区域内展开为幂级数和幂的负次幂的和。

复变函数泰勒级数展开条件
泰勒级数是将函数在某一点附近展开成幂级数的一种方法，它在求解复变函数的性质中有着重要的应用。

但是，不是所有的函数都能够通过泰勒级数展开来表示，下面我们就来探讨一下复变函数泰勒级数展开的条件。

设f(z)在z0的某个邻域内解析，则f(z)在z0处的泰勒级数为 $f(z)=sum_{n=0}^{infty}
frac{f^{(n)}(z_0)}{n!}(z-z_0)^n$
其中$f^{(n)}(z_0)$为f(z)在z0处的n阶导数。

那么，f(z)能否通过泰勒级数展开来表示呢？
对于实变函数来说，泰勒级数展开的条件是函数在展开点处有无穷阶导数。

但对于复变函数来说，情况要更为复杂。

我们可以通过考虑柯西-黎曼方程来求解这个问题。

根据柯西-
黎曼方程，如果f(z)在某个区域内可解析，则它在该区域内满足以下条件：
$frac{partial u}{partial x}=frac{partial v}{partial y}$ $frac{partial u}{partial y}=-frac{partial v}{partial x}$ 其中，f(z)=u(x,y)+iv(x,y)。

根据这个条件，我们可以得到如下结论：
当f(z)在z0处可解析时，它在z0处的泰勒级数展开收敛于f(z)的充要条件是：
1. f(z)在z0的某个邻域内解析。

2. f(z)在z0处有无穷阶导数。

3. 泰勒级数在z0处收敛于f(z)。

4. f(z)在z0处的导数的幅值不超过某一常数。

这些条件是复杂函数泰勒级数展开的基本要求，只有同时满足这些条件，才能通过泰勒级数展开来表示复变函数。

泰勒定理与洛朗定理的联系与区别1 引言泰勒定理和洛朗定理是复变函数中极其重要的定理．泰勒定理给出了解析函数在解析点邻域内的具体展式，而洛朗定理是研究解析函数在其孤立奇点去心邻域内性质的重要工具．它们既有相同点又有不同点．因此，研究它们的联系和区别是很有必要的．在此之前，许多数学工作者对这方面的研究已经取得很好的成果．本文的论述是在前人成果的基础上对已有的知识进行有效的归纳和总结．2 泰勒定理与洛朗定理的介绍2.1 泰勒定理 定理１（泰勒定理）()162159]1[-P设) ( z f 在区域D 内解析，D a ∈，只要圆R a z <-K ：含于D ，则) ( z f 在K 内能展成幂级数nn n a z c z f )() ( 0-=∑∞= ， (1)其中系数 ()!)()()(211n a f d a f i c n n n =-=⎰Γ+ζζζπρ ． (2)（积分形式） （微分形式）() 2100，，，，：=<<=-Γn R a ρρζρ且展式是惟一的．定义1()162]1[P(1)称为) ( z f 在点a 的泰勒展式，（2）称为其泰勒系数，而(1)等号右边的级数，则称为泰勒级数．2.2 洛朗定理 定理２（洛朗定理）()188185]1[-P在圆环()∞≤≥H ＋，＜－＜：R r R a z r 0内解析的函数) ( z f 必可展成双边幂级数nn na z c z f )() ( -=∑∞-∞= ， （3）其中() ,2,1,0)()(211±±=-=⎰Γ+n d a f i c n n ζζζπ， (4)Γ为圆周()R r a <<=-ρρζ，并且展式是惟一的（即) ( z f 及圆环H 惟一地决定了系数n c -）． 定义２()188]1[P (3)称为) ( z f 在点a 的洛朗展式，(4)称为其洛朗系数，而(3)等号右边的级数则称为洛朗级数．3 泰勒定理与洛朗定理的比较3.1 泰勒定理与洛朗定理的联系先就定理要求的可展区域来讨论它们的联系．函数在圆内展成泰勒级数，在圆环内展成洛朗级数．假设当已给函数) ( z f 在点a 处解析时，中心在点a ，半径等于由点a 到函数) ( z f 的最近奇点的距离的那个圆可以看成圆环的特殊情形，在那个圆中就可以作出洛朗级数展开式．根据柯西积分定理，由公式(4)可以看出，这个展式的所有系数n c -() ,2,1=n 都等于零．在这种情形下，计算洛朗级数的系数公式与泰勒级数的系数公式的积分形式是一致的，所以，洛朗级数就转化成泰勒级数．因此，泰勒级数是洛朗级数的特殊情形．另一方面，我们从展式的展法和系数上讨论它们的联系．计算洛朗级数的系数公式在形式上和泰勒级数的系数公式（积分形式）是一致的．用直接展开法求级数要计算积分，很麻烦．而圆域内解析函数的泰勒级数展开式是惟一的，在求一些初等函数的泰勒级数时，就不用直接展开法，而可以利用已知的泰勒级数去求所需要的泰勒级数，即间接展开法．同泰勒级数情形一样，圆环域内解析函数的洛朗级数展开式也是惟一的，也可以利用间接展开法去求．在展开函数为洛朗级数时,以泰勒级数为基础．下面，举一个用直接展开法展成泰勒级数的例子． 例１ 将函数z z f 2sin ) ( =展为z 的泰勒级数.解 z z f 2sin ) ( =' )22(sin 2) ( π+=''z z f()()⎥⎦⎤⎢⎣⎡-+⋅=-212sin 2) ( 1πn z z fn n 当n 为奇数时, ()0!)0( =n f n当n 为偶数时,令+Z ∈=k k n ,2()()⎥⎦⎤⎢⎣⎡-⋅=-212sin 2!)2 (1!)2 ( )0 ( 122πk k k f k k 112)1 (2!)2 (1+--⋅=k k k所以 -+-=654322!62!42!22sin z z z z )(∞<z 对于直接展开法，就不再赘述了，这里，我们简单介绍泰勒级数与洛朗级数的间接展开法． 间接展开法是利用已知函数展开式，结合解析函数性质、幂级数运算性质和其他数学技巧，求函数的级数展开式．常用的一些方法有代换法、部分分式法、柯西乘积法等．除了上述方法外，还可以利用组合、搭配等方法把一个解析函数展开为级数．注意，一个函数可以用多种方法展开，但是其展开式是惟一的．在下面讲关于泰勒定理与洛朗定理的区别时，我们再做具体全面的比较．3.2泰勒定理与洛朗定理的区别先介绍一些初等函数在0=z 处的泰勒级数，它们可以用来间接地求函数的级数展开式． （1）+++++=-n z z z z2111)1 (<z （2）()()+-+-+-=!21!4!21cos 242n z z z z nn) (∞<z（3）()()()()++--++-++=+n z n n z z z !11!21112ααααααα)1 (<z（4） +++++=!!212n z z z e nz) (∞<z（5）()() +-+-+-=+-nz z z z z nn 1321321ln )1 (<z 泰勒定理中要求函数) ( z f 在区域D 内解析，D a ∈，圆R a z <-K ：含于D ，则) ( z f 在K 内能展成泰勒级数，就是说泰勒级数的收敛区域为一个圆．泰勒展式仅限于z 在ρΓ的内部时方能成立，而ρΓ又只需在) ( z f 的解析区域D 内就行，其大小并无限制．故展式在以a 为中心，通过与a 最接近的) ( z f 之孤立奇点的圆周内部皆成立．用泰勒定理来表示圆形区域内的解析函数是很方便的，但是，对于有些函数) ( z f ，若点a 为) ( z f 的孤立奇点，在点a 的邻域内就不能展为泰勒级数．洛朗定理建立了（挖去奇点a 的）圆环(0,r z a R r R <-<>≤+∞,当0=r 时为去心圆)R a z <-<0内解析函数的级数表示，即在圆环()+∞≤><-<H R r R a z r ,0：内解析的函数) ( z f 必可展成洛朗级数（即双边幂级数)，例如函数zz f 1) ( =，0=z 为孤立奇点，在0z <<+∞内就可以展开为洛朗级数． 下面举例说明函数在不同区域展为不同级数． 例1 将函数()()211) ( --=z z z f 在如下三个解析区域:(1) 圆1<z ;(2) 圆环21<<z ;(3) 圆环+∞<<z 2内展为级数.解 首先将函数) ( z f 分解成部分分式 1121) ( ---=z z z f (1) 在圆1<z 内,因21<<z ,即12<z,得 ⎪⎭⎫ ⎝⎛---=212111) ( z z z f()⎪⎪⎭⎫ ⎝⎛+++-+++= 222221211z z z z+++=2874321z z（函数) ( z f 在圆1<z 内展为泰勒级数）.(2) 在圆环21<<z 内,即有11<z ,12z< z z z z f 111121121) ( -⋅--⋅-=⎪⎭⎫⎝⎛+++-⎪⎪⎭⎫ ⎝⎛+++-= 222111122121z z z z z-----------=-n n n z z z z z z z 222211111132223（函数 ( )f z 在圆环21<<z 内展为洛朗级数）.(3) 在圆环+∞<<z 2内,这时11<z ,21z<故z z z z z f 11112111) ( -⋅--⋅=⎪⎭⎫⎝⎛+++-⎪⎪⎭⎫ ⎝⎛+++= 22211112211z z z z z z+++=432731zz z（函数 ( )f z 在圆环2z <<+∞ 内展为洛朗级数）.由此例可以看出，函数在圆内展为泰勒级数，而在圆环内展为洛朗级数．又注意到，只要函数在指定的圆环内解析就能在该圆环内展为洛朗级数．从而，同一个函数在不同的圆环内（只要它在此圆环内解析）都能展为洛朗级数．当然，同一个函数在不同的圆环内展成的洛朗级数可能是不同的．这与洛朗展式的惟一性并不矛盾．下面讲几种展开方法，并列举例子来进行对比．我们可以简单地体会一下它们在展法上的区别． (１) 代换法代换法的关键是将) ( z f 变形为含所需因式的形式，并可以利用已知展开式得到需要的级数.例２ 将函数()221) ( +=z z f 在0=z 和1=z 处展为泰勒级数．解（１）当0z =时，化()()22214121-⎪⎭⎫⎝⎛+=+=z z z f ，并利用已知级数展开式 ()()()() ++--++-++=+n z n n z z z !11!21112ααααααα ()1<z令12<z，当2-=α时，即可得()22214121-⎪⎭⎫ ⎝⎛+=+z z ⎪⎪⎭⎫ ⎝⎛-⋅⋅+⋅-= 222!2322!12141z z -+-=1634412z z ()2<z（２）当1=z 时，化函数()()223119121-⎪⎭⎫ ⎝⎛-+=+=z z z f 令131<-z ，即可得()()⎥⎦⎤⎢⎣⎡--⋅⋅+-⋅-⋅=+ 2223!213231219121z z z()() --+--=2712712912z z()31<-z例３ 将()11) ( -=z z z f 在10<<z 展为洛朗级数．解 由已知泰勒级数展开式()1,1112<+++++=-z z z z zn故 ()zz z z z f 11111) ( --=-=z z 111---= ()+++--=211z z z-----=211z z z()10<<z由例２看出，函数在解析点0=z 和1=z 的对应圆域内展为泰勒级数，该级数只含有正幂次项，但是对于不同的解析点，其收敛圆域不同，泰勒级数形式也不同，所以，在展为泰勒级数时要注意函数在哪点展开．由例３看出，函数在孤立奇点0=z 的去心邻域（圆环）内展为洛朗级数，该级数不仅仅含有正幂次项，而且含有负幂次项．其中∑∞==-011n n z z 代换()1<z 是函数展为级数时用得最多,也是最为简便的一种代换．即要展为a z -的泰勒级数,先将函数变形,使之出现a z -的形式,但是要注意,由于因式的转变,收敛圆也要改变. 对于洛朗展式，要将函数()0) ( ≠+=a baz cz f 展开,关键在于将) ( z f 变形,使表示式中出现w-11因式,且1<w .这里w 的取定还跟圆环域的中心与半径有关. (2) 部分分式法当) ( z f 为有理分式函数时,一般可先分解为部分分式,然后再利用已知级数展开.例４ 将函数()()321) ( ++=z z z f 在0=z 展为泰勒级数．解 化()()321) ( ++=z z z f 为部分分式3121) ( +-+=z z z f 其中2112121z z +⋅=+ ⎪⎪⎭⎫ ⎝⎛+-+-= 3322222121z z z +-+-=4332222221z z z ()2<z3113131z z +⋅=+⎪⎪⎭⎫ ⎝⎛+-+-= 3322333131z z z +-+-=4332233331z z z ()3<z3121) ( +-+=z z z f ⎪⎪⎭⎫⎝⎛+-+--⎪⎪⎭⎫ ⎝⎛+-+-= 43322433223333122221z z z z z z-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=23322312131213121z z()2<z例５ 将函数()211) ( z z z f -=在其孤立奇点的去心邻域内展为洛朗级数．解 0=z ，1=z 为函数的孤立奇点，化为部分分式 在0=z 的（最大）去心邻域10<<z 内()()221111111) ( z z z z z z f -+-+=-=()()222111++++++++=z z z z z ++++=24321z z z()10<<z在1=z 的（最大）去心邻域110<-<z 内()()()22111111111) ( -+---+=-=z z z z z z f ()()()[]()23211111111-+--+---+--=z z z z z ()()()() +---+--+---=32211111111z z z z z ()110<-<z由例４，函数在圆域内展为泰勒级数，该级数只有正幂次项．而由例５看出，函数在孤立奇点的去心邻域内展为洛朗级数，不仅有正幂次项，而且含有负幂次项．注意到，同一个函数对不同的孤立奇点的洛朗展式不同．只要函数在指定的圆环内解析就能在该圆环内展为洛朗级数．从而，同一个函数在不同的圆环内（只要它在此圆环内解析）都能展为洛朗级数．孤立奇点的去心邻域就是圆环的特殊情形，与洛朗定理一致． （３）柯西乘积法当函数可以分解为两个已知展开式的函数的乘积时，我们用柯西乘积法求所求泰勒级数的展开式．一般用对角线法则确定泰勒级数的项，对于求洛朗级数时也可以用此法．例６ 将ze zf z-=1) ( 展为z 的泰勒级数．解 因ze zf z-=1) ( 在1<z 内解析，故展开后的泰勒级数在1<z 内收敛．已知ze z e zf z z -⋅=-=111) (()+++++⋅⎪⎪⎭⎫ ⎝⎛+++++=nn z z z n z z z 221!!21 +⎪⎪⎭⎫ ⎝⎛++++++⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛++=nz n z z !1!21!111!21!111!11112 ()1<z例７ 将()()12ln ) ( --=z z z z f 在10<<z 展为洛朗级数． 解 ()()()112ln 112ln ) ( -⋅-⋅=--=z z z z z z z f⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅-⋅-=21ln 2ln 111z z z()⎪⎪⎭⎫ ⎝⎛-⋅-⋅--⋅++++⋅-=332232232222ln 11z z z z z z z-⎪⎪⎭⎫ ⎝⎛⋅-⋅---⎪⎪⎭⎫ ⎝⎛⋅---⎪⎭⎫ ⎝⎛---=2322231221212ln 221212ln 212ln 2ln z z z ()10<<z由例６，函数在圆域内展为泰勒级数．而由例７看出，函数在孤立奇点0=z 的去心邻域内展为洛朗级数．只要点a 为函数) ( z f 的一个孤立奇点，则必存在正数R ，使得) ( z f 在点a 的去心邻域{}R a z a ＜－＜：0-K 内展为洛朗级数．其它的展法就不一一说明了，可以类似方法加以讨论．从上述讨论可以看出，泰勒级数与洛朗级数是一般与特殊的关系．从级数的结构上看，洛朗级数是泰勒级数的推广，它们的系数公式的积分形式是一致的，不同的是，泰勒级数只含有正幂次项，而洛朗级数既含有正幂次项又含有负幂次项．另一方面，若函数) ( z f 在0z 点解析，那么) ( z f 在以0z 点为中心的解析圆域内可用泰勒级数表示，然而若0z 点为函数的孤立奇点，但函数在0z 点的某个圆环内解析，此时就不能用泰勒级数表示而可用洛朗级数表示．参考文献[1] 钟玉泉.复变函数学习指导书[M].北京：高等教育出版社，2005 [2] 余家荣.复变函数[M].第三版. 北京：高等教育出版社，2004 [3] 钟玉泉.复变函数论[M].第三版. 北京：高等教育出版社，2004 [4] 方企勤.复变函数教程[M].北京：北京大学出版社，2003 [5] 郑建华.复变函数[M].北京：清华大学出版社，2005[6] 孙清华,赵德修.新编复变函数题解[M].武汉：华中科技大学出版社，2001[7] Robert Everist Greene.Function theory of one complex variable[M].American Mathematical Society ，2006。