当前位置：文档之家 › 复变函数：泰勒级数

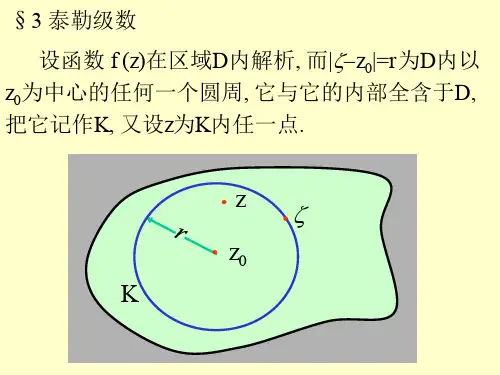
复变函数：泰勒级数

  • 格式：ppt
  • 大小：350.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

复变函数 级数

复变函数 级数

+∞ ( zi ) n +∞ ( − zi ) n 1 = ∑ −∑ 2i n = 0 n! n! n=0
1 +∞ 2i 2 k −1 z 2 k −1 +∞ ( −1) k −1 z 2 k −1 = ∑ =∑ 2 i k =1 ( 2k − 1)!! k =1 ( 2k − 1)!! z z z ( − 1) z ∴ sin z = z − + − + L = ∑ 3! 5! 7! k = 1 ( 2 k − 1)! !
定理（泰勒展开定理） 定理（泰勒展开定理） 设 f ( z )在区域 D 内解析 , z 0 ∈ D , R 为 z 0 到 D 的边界
上各点的最短距离 f (z) =
∞
⇒ 当 z − z0 < R时 , (1 )
f ( z )在 z 0处 的 Taylor 级数
cn ( z − z0 )n ∑
n=0 (n)
( z − z0 )n + 2π i
f ( n ) ( z0 ) ( z − z0 ) n + L (4) = f ( z0 ) + f ' ( z0 ) + L + n! − −函数 f ( z )在 z 0处的 Talor 级数
为中心， 级数 ( 4 )的收敛范围是以 z 0为中心， r为半径 的圆域 ζ − z 0 < r ,圆 k的半径 r可以任意增大 , 只要圆 k及其内部包含在 D内即可 ,∴ f ( z )在 解析点 z 0处的 Taylor 级数收敛半径至少等于 从 z 0到 D的边界上各点的最短距 离.证毕 !
(不讲 两端乘以 f (ζ ) , 沿着 k逐项积分得 , 不讲) 不讲 2π i 1 f (ζ ) 1 f (ζ ) f (z) = ∫k ζ − z dζ = 2πi ∫k ζ − z0 dζ 2π i

泰勒极数

泰勒极数

2
i
f
(
(
) z0
)n1
(
z
z0
)n
f ( )
2 z0
n
z z0
z0
M
2
r
z z0 r
n
M qn,
2 r
其中,
q
z z0 r
1.
可知在C上是一致收敛
前面积分号下的级数可在C上逐项积分.
再根据 Cauchy导数公式
f (z)
1
2 i
c
定理f2.(6 n0 ( z0
2!
n!
并且收>>敛ta半yl径or(fR,z) %展. 开的默认值是6项
ans =
2. 间接方法 借助于一些已知函数的展开式 , 结合解析
函数的性质, 幂级数运算性质 (逐项求导, 逐项 积分等)和其它的数学技巧 (代换等) , 求函数的 Taylor展开式.
间接法的优点: 不需要求各阶导数与收敛半径 , 因而比直
负实轴>>向sy左m的s z射; 线的区域内解析.
>> f=log(1+z);
y
因为
>> taylor(f)
R1
lna(n1s=z) 1 ,
1 z
1 o 1
x
z-1/2*z^2+1/3*z^3-1/4*z^4+1/5*z^5
1 1 z z2 (1)n zn
z 1 ,
1 z
所以
ln(1 z)
z 1 ,
1 z
逐项求导，得
1
(1 z)2
1 2z
3z2
(1)n(n 1)zn
z 1 .

实验一计算复变函数极限、微分、积分、留数、泰勒级数展开式

实验一计算复变函数极限、微分、积分、留数、泰勒级数展开式

实验一计算复变函数极限、微分、积分、留数、泰勒级数展开式【实验目的】1、熟悉Matlab运行环境，会在窗口操作和运行一些命令2、掌握求复变函数极限、微分、积分、留数以及泰勒级数命令3、熟练在计算机上操作复变函数极限、微分、积分、留数以及泰勒级数命令【实验仪器】一台电脑，要求安装matlab 软件【实验内容】MATLAB实现内容1、MATLAB求复变函数极限2、MATLAB求复变函数微分3、MATLAB求复变函数积分4、MATLAB求复变函数在孤立奇点的留数5、MATLAB求复变函数的泰勒级数展开式【实验步骤】1．打开matlab桌面和命令窗口，方式一，双击桌面快捷方式，方法二，程序里单击matlab图标，方式三，找到matlab文件夹，双击图标2．在matlab命令窗口输入命令3．运行，可以直接回车键，F5键【注意事项】1．命令的输入要细心认真，不能出错2．尤其是分号，逗号等符号的区别3. 注意数学上的运算和matlab中的不同，尤其是括号【实验操作内容】以下的例题都是在命令窗口输入源程序，然后运行，或回车就可以得到结果。

1、MATLAB 求复变函数极限用函数limit 求复变函数极限【Matlab 源程序】syms zf=;limit(f,z,z0) 返回极限结果例 1 求 在 的极限 解 【Matlab 源程序】syms zf=sin(z)/z;limit(f,z,0)ans=1limit(f,z,1+i)ans=1/2*sin(1)*cosh(1)-1/2*i*sin(1)*cosh(1)+1/2*i*cos(1)*sinh(1)+1/2*cos(1)*sinh(12、 MATLAB 求复变函数微分用函数diff 求复变函数极限【Matlab 源程序】zz z f sin )(=i z +=1,0f=（）;diff(f,z) 返回微分结果解 syms zf=exp(z)/((1+z)*(sin(z)));diff(f)ans =exp(z)/(1+z)/sin(z)-exp(z)/(1+z)^2/sin(z)-exp(z)/(1+z)/sin(z)^2*cos(z)3、 MATLAB 求复变函数积分用函数int 求解非闭合路径的积分.【Matlab 源程序】syms z a bf=int(f,z,a,b) 返回积分结果解 syms zx1=int(cosh(3*z),z,pi/6*i,0)x2=int((z-1)*exp(-z),z,0,i)结果为：例 3 求积分 π60i i 0x1=ch3zdz; x2(1)d z z e z -=-⎰⎰例2 设()()z f z z e z f z'+=求,sin 1)(x2 = -i/exp(i)4、 MATLAB 求复变函数在孤立奇点的留数（1）f(z)=p(z)/q(z)；p(z)、q(z)都是按降幂排列的 多项式用函数residue 求f(z)=p(z)/q(z)在孤立奇点的留数【Matlab 源程序】[R,P,K]= residue (B,A) 返回留数，极点说明：向量B 为f(z)的分子系数；向量A 为f(z)的分母系数；向量R 为留数；向量P 为极点位置；向量k 为直接项:例4 求函数 在奇点处的留数． 解 [R,P,K]= residue([1,0,1],[1,1])结果为：R= 2P = -1K = 1 -15、MATLAB 求复变函数的泰勒级数展开式（1）用函数taylor 求f(z)泰勒级数展开式【Matlab 源程序】112++z zf=Taylor(f,z0) 返回f(z)在点z0泰勒级数展开式例5 求函数f=1/(z-b)在点z=a泰勒级数展开式前4项syms z a b;f=1/(z-b);taylor(f,z,a,4)ans =1/(a-b)-1/(a-b)^2*(z-a)+1/(a-b)^3*(z-a)^2-1/(a-b)^4*(z-a)^3（2）求二元函数z=f(x,y)在点（x0,y0）的泰勒级数展开式.【Matlab源程序】syms x y; f=();F=maple(‘mtaylor’,f,‘[x,y]’,m) 返回在(0,0)点处的泰勒级数展开式的前m项.F=maple(‘mtaylor’,f,‘[x=x0,y=y0]’,m) 返回在(x0,y0)点处的泰勒级数展开式的前m项.F=maple(‘mtaylor’,f,‘[x=a]’,m) 返回对单变量在x=a处的泰勒级数展开式的前m项.例6 求函数222==-z f x y x x e---(,)(2)x y xy在原点(0，0)，以及（1，a）点处的Taylor展式．【Matlab源程序】syms x y;f=(x^2-2*x)*exp(-x^2-y^2-x*y);maple(‘mtaylor’,f,‘[x,y]’,4)在(0,0)点处的泰勒级数展开式：ans =-2*x+x^2+2*x^3+2*y*x^2+2*y^2*xmaple(‘mtaylor’,f,‘[x=1,y=a]’,2)在(1,a)点处的泰勒级数展开式：ans =-exp(-1-a-a^2)-exp(-1-a-a^2)*(-2-a)*(x-1)-exp(-1-a-a^2)*(-2*a-1)*(y-a)maple(‘mtaylor’,f,‘[x=a]’,2) 在x=a处泰勒级数展开式：ans =(a^2-2*a)*exp(-a^2-y^2-a*y)+((a^2-2*a)*exp(-a^2-y^2-a*y)*(-2*a-y)+(2*a-2)*exp(-a^2-y^2-a*y))*(x-a)。

复变函数泰勒级数展开

复变函数泰勒级数展开
泰勒级数展开在概率论与数理统计中也有应用，例如在中 心极限定理的证明中就使用了泰勒级数展开的方法。05结论泰勒级数展开的重要性和影响
理论意义
泰勒级数展开是复分析中的重要工具，它为研究函数的性 质提供了理论基础，有助于深入理解函数的性质和行为。
应用价值
泰勒级数展开在数学、物理、工程等多个领域都有广泛的应用 ，例如在信号处理、控制系统、量子力学等领域，泰勒级数展 开都发挥了关键作用。
指数函数e^z的泰勒级数展开
总结词
指数函数e^z在复平面上的泰勒级数展开 式为无限和的形式，可以表示为幂级数 的和。
VS
详细描述
e^z = 1 + z + z^2/2! + z^3/3! + ... + z^n/n! + ...，其中z为复数，n!表示n的阶 乘。这个级数是无限和的形式，可以用于 近似计算e^z的值。
对数学发展的推动
泰勒级数展开的发现和证明对数学的发展产生了深远的影响， 它不仅推动了复分析的兴起和发展，还为数学的其他分支提供 了新的思路和方法。
对未来研究的展望
深入研究泰勒级数展开的性质和特性
尽管泰勒级数展开已经得到了广泛的研究和应用，但关于其性质和特性的研究仍有许多值得深入探讨的问题，例如高 阶泰勒级数展开、非标准泰勒级数展开等。
值，并帮助理解函数的性质和行为。
04
泰勒级数展开的应用
在微积分中的应用
函数逼近
泰勒级数展开可以用来逼近复杂的函数，通过将复杂的函 数表示为简单的多项式之和，可以更好地理解和分析函数 的性质。
无穷级数求和
泰勒级数展开可以用来求无穷级数的和，这对于解决一些 数学问题非常有用，例如求定积分等。
数值分析

高等数学课件-复变函数与积分变换 第四章 级数

高等数学课件-复变函数与积分变换 第四章 级数

称为级数的部分和。
在收敛域D内
lim
n
Sn
(
z)
S
(
z
),
S ( z) 为级数的和函数。
二、幂级数
若 fn (z) Cn zn 或 fn (z) Cn (z z0 )n 时，
幂级数为
Cn zn 或
Cn (z z0 )n
n0
n0
定理4.7
Ab el 定理如果级数
Cn zn
n0
z z 在
z0
sin
z
k 0
(1)k z2k1
2k 1!
R
• 例5 将 cos z 在 z 0处展开成幂级数。
sin z 解： 将
两边对z求导
cos z
(1)k (2k 1)z2k
k 0
2k 1!
(1)k z2k
k 0
2k !
例6 arctan z 在 z 0 处展开成幂级数。
解：
arctan
z
b
二、复数项级数
定义4.2
z 设
为一复数列，表达式
n
zn z1 z2 zn
n1 为复数项级数，其前n项之和
Sn z1 z2 zn
为级数的部分和。 称级数收敛，
若
lim
n
Sn
S,
S称为级数的和，
记为
S zn
若
{Sn} 不收敛，则称级数是发散的
n1
n
n
n
Sn k an i bn 有
收敛，那么对满足
0
| z || z0 | 的z，
级数必绝对收敛。
如果在
z z 级数发散，那么对满足 0

大学物理2.3 复变函数在环形区域中的幂级数展开

大学物理2.3 复变函数在环形区域中的幂级数展开

2. 将有理式分解为部分分式，再按 3. 利用两个绝对收敛级数的乘积。 4. 利用逐项求导或逐项积分。
展开。
例子：将
以 z = 0 中心展开成幂级数。
分析：展开中心 z = 0 不是 f (z) 的奇点，奇点为 –1、2。
解：
的三个解析区域 |z| < 1, 1< |z| <2, 2 < |z| <∞
2.3 复变函数在环形区域中的幂级数展开
泰勒级数：在一个圆域内展开 收敛半径 R：若 R = 0，函数只在该点解析；若 R 为有限值， 函数在某一圆内解析； 若 R = ，函数在全平面解析。 例如：f (z) = 1/(1– z) 只能在 |z| < 1 展开成泰勒级数，因为
z = 1 是函数的奇点，不能在全平面把它展开成泰勒 级数，但是在 |z| > 1 区域，它又是解析的，那么能 否在 |z| > 1 的区域把 f (z) 展开成级数呢？
Jm (t)
l0
(1)l m
l !(l
1
( t )m2l m)! 2
(1)m Jm (t) (m 0,1, 2, )
Jn (t) 称为 n 阶贝塞尔函数 (参看§9-1)。
例：以 z = 0 为中心在 1 < |z| < 展开 解：
展开中心为 z = 0，故只需展开
[分子已为 z =(z–0)1 ]
有
第二个积分中： | b| < |z b|
令 –(n+1) = k，则 n = 0 时：k = –1；n = 时： k = – 上式变为：
其中：
说明：
(1) 洛朗级数中 ak 积分表达式与泰勒系数形式相同，但洛朗 系数无微分形式。因为：高阶导数公式要求 f (z) 解析才 成立。但在此 f (z) 仅在 R2 < | z – b | < R1 区域内解析；

复变函数§3 泰勒级数


2
n
当z沿实轴从单位圆内部趋 近于1时：f (z)
即z 1是一个奇点。

推论4：设函数
f
(
z)在z
解析，且有
0
Taylor展开式：f (
z
)


Cn
(
z
-
z0
)n
,
n0
a是f (z)的距z0最近的一个奇点， 则R a - z0 为其收敛半径。
例如：f
(z)

z2
1 z
-6


f (z) cn (z - z0 )n 成立, 其中 n0
cn

1 n!
f
(n) (z0 ), n

0,1, 2,
.
注： 如果 f (z)在z0解析, 则使 f (z)在z0的泰勒展开式 成立的圆域的半径 R等于从z0到 f (z)的距z0最近一个奇点
a 的距离, 即R=|a-z0|.
y
n1
因此, 只有在R1<|z-z0|<R2的圆环域, 原级数才收敛.
例如级数

n1
an zn

n0
zn bn
(a与b为复常数)
R2 z0 R1

中的负幂项级数
an
zn
n1

n1

a z
n
,当
a z
1,

即| z || a | 时收敛,而正幂项级数
,
0 1
0
0
即 ln(1 z) z - z2 z3 - (-1)n zn1 | z | 1.ຫໍສະໝຸດ 23n 1推论1：

复变函数4-2Taylor级数


f
( n) ( z0
)
,
n 0,1,2,
例如，求 ez 在 z 0的泰勒展开式.
因为(ez )(n) ez ,
(ez )(n) z0 1, (n 0,1, 2,)
故有 ez 1 z z2 zn zn
2!
n!
n0 n!
因为ez 在复平面内处处解析,
[ln(1 z)] 1 1 z z2 1 z

(1)n zn
(1)n zn
( z 1)
n0
设 C 为收敛圆 z 1内从 0 到 z 的曲线,
将展开式两端沿 C 逐项积分, 得
z 1 dz z (1)n zndz
01 z
2! 4!
(2n)!
(R )
2. 间接展开法 :
借助于一些已知函数的展开式 , 结合解析
函数的性质, 幂级数运算性质 (逐项求导, 积分
等)和其它数学技巧 (代换等) , 求函数的Taylor
展开式.
间接法的优点:
不需要求各阶导数与收敛半径 , 因而比直
接展开更为简洁 , 使用范围也更为广泛 .
1 z
n0
z3 z5 4) sin z z
(1)n
z 2n1

( z 1)
3! 5!
(2n 1)!

= (1)n
z 2n1
n0
(2n 1)!
( z )
z2 z4 5) cos z 1
(1)n z2n
2! 4!
(2n)!
0 n0
即 ln(1 z) z z2 z3 (1)n zn1 z 1

复变函数复习资料

复变函数复习资料复变函数是数学中的一个重要分支，它研究的是具有复数变量和复数值的函数。

复变函数的研究对于数学的发展和应用有着重要的意义。

在这篇文章中，我将为大家提供一些复变函数的复习资料，希望对大家的学习有所帮助。

一、复变函数的基本概念复变函数是指定义在复数域上的函数，它的自变量和因变量都是复数。

复变函数可以表示为f(z)=u(x,y)+iv(x,y)，其中z=x+iy，u(x,y)和v(x,y)分别是实部和虚部函数。

复变函数的导数和积分也有相应的定义，与实数函数的导数和积分有一些不同之处。

二、复变函数的解析性与调和性复变函数的解析性是指函数在某个区域内处处可导，它是复变函数的重要性质。

根据柯西—黎曼方程，只有满足一定条件的函数才能是解析函数。

解析函数具有很多重要的性质，例如它的实部和虚部都是调和函数，它的导数也是解析函数。

三、复变函数的级数表示复变函数可以用级数表示，这是复变函数研究中常用的一种方法。

泰勒级数是复变函数的一种重要的级数表示形式，它可以将函数展开成一系列幂函数的和。

而洛朗级数则是将函数展开成一系列幂函数和互补幂函数的和，适用于具有奇点的函数。

四、复变函数的积分复变函数的积分是复分析中的重要内容，它与实数函数的积分有一些不同之处。

复变函数的积分可以沿着一条曲线进行，这就是复积分的概念。

复积分有一些重要的性质，例如柯西—黎曼积分定理和柯西公式等，它们在复分析中有着广泛的应用。

五、复变函数的应用复变函数在物理学、工程学和计算机科学等领域有着广泛的应用。

它可以用来描述电磁场、流体力学和信号处理等问题。

复变函数的解析性和级数表示等性质使得它在实际问题的求解中具有很大的优势。

总结：复变函数是数学中的一个重要分支，它研究的是具有复数变量和复数值的函数。

复变函数的解析性、级数表示和积分等性质是复变函数研究的核心内容。

复变函数在物理学、工程学和计算机科学等领域有着广泛的应用。

希望通过这些复习资料，能够帮助大家更好地理解和掌握复变函数的知识。

复变函数泰勒级数展开条件

复变函数泰勒级数展开条件
泰勒级数是将函数在某一点附近展开成幂级数的一种方法，它在求解复变函数的性质中有着重要的应用。

但是，不是所有的函数都能够通过泰勒级数展开来表示，下面我们就来探讨一下复变函数泰勒级数展开的条件。

设f(z)在z0的某个邻域内解析，则f(z)在z0处的泰勒级数为 $f(z)=sum_{n=0}^{infty}
frac{f^{(n)}(z_0)}{n!}(z-z_0)^n$
其中$f^{(n)}(z_0)$为f(z)在z0处的n阶导数。

那么，f(z)能否通过泰勒级数展开来表示呢？
对于实变函数来说，泰勒级数展开的条件是函数在展开点处有无穷阶导数。

但对于复变函数来说，情况要更为复杂。

我们可以通过考虑柯西-黎曼方程来求解这个问题。

根据柯西-
黎曼方程，如果f(z)在某个区域内可解析，则它在该区域内满足以下条件：
$frac{partial u}{partial x}=frac{partial v}{partial y}$ $frac{partial u}{partial y}=-frac{partial v}{partial x}$ 其中，f(z)=u(x,y)+iv(x,y)。

根据这个条件，我们可以得到如下结论：
当f(z)在z0处可解析时，它在z0处的泰勒级数展开收敛于f(z)的充要条件是：
1. f(z)在z0的某个邻域内解析。

2. f(z)在z0处有无穷阶导数。

3. 泰勒级数在z0处收敛于f(z)。

4. f(z)在z0处的导数的幅值不超过某一常数。

这些条件是复杂函数泰勒级数展开的基本要求，只有同时满足这些条件，才能通过泰勒级数展开来表示复变函数。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

z z0 z z0 令 q， z z0 r
q与积分变量z无关, 且0q<1.
K
z z z0
复变函数与积分变换
Complex Analysis and Integral Transform
K含于D, f (z) 在D内解析, 在K上连续, 在K上有界, 因此在K上存在正实数 M 使| f (z) | M.
复变函数与积分变换
Complex Analysis and Integral Transform
泰勒级数
设函数f ( z )在区域D内解析，而 z z0 r为D内以z0为 中心的任何一个圆周，记作K，圆周及它的内部全含于D， 又设z为K内任一点。
z
z
z0
K
复变函数与积分变换
Complex Analysis and Integral Transform
.
z
因为ez在复平面内处处解析, 上式在复平面内处处成立, 收敛半径为+. 同样, 可求得sinz与cosz在z=0的泰勒展开式:
复变函数与积分变换
Complex Analysis and Integral Transform
z3 z5 sin z z 3! 5! z2 z4 cos z 1 2! 4!
z 2 n 1 (1) (2n 1)!
n 2n z (1) n (2n)!
z z
除直接法外, 也可以借助这些已知函数的展开式, 利用 幂级数的运算性质和分析性质, 以唯一性为依据得出函数的 泰勒展开式, 此方法称为间接展开法. 例如sin z在z=0的泰 勒展开式也可以用间接展开法得出:
N 1
由解析函数高阶导数公式,上式可写成
f ( z)
n 0 N 1
f ( n ) ( z0 ) ( z z0 ) n RN ( z ) n!
其中
K
z z z0
ቤተ መጻሕፍቲ ባይዱ
1 RN ( z ) 2πi
f (z ) n ( z z0 ) d z n 1 (z z0 ) K n N
f ( z ) cn ( z z0 ) n
n 0
成立 , 其中
1 (n) cn f ( z0 ), n 0,1, 2, n!
.
注：如果f (z)在z0解析,则使f(z)在z0的泰勒展开式 成立的圆域的半径 R 等于从z0到f(z)的距z0最近一个奇点 a 的距离, 即R=|a-z0|.
1 iz iz 1 (iz ) n (iz ) n sin z (e e ) 2i 2i n 0 n ! n 0 n ! 2 n 1 z3 z5 z z (1) n z 3! 5! (2n 1)! n 0
复变函数与积分变换
Complex Analysis and Integral Transform
如果能证明 lim RN ( z ) 0在K内成立, 则
N
f ( z)
n 0

f
(n)
( z0 ) ( z z0 ) n n!
在K内成立, 即 f (z)可在K内 用幂级数表达.
复变函数与积分变换
Complex Analysis and Integral Transform
因此, 下面的公式在K内成立:
f ( z)
n 0
f ( n ) ( z0 ) ( z z0 ) n n!
称该等式为f (z)在z0点的泰勒展开式, 它右端的 级数称为 f (z)在z0处的泰勒级数.
圆周K的半径可以任意增大, 只要K在D内. 所 以,如果z0到D的边界上各点的最短距离为d,则f(z) 在z0点的泰勒展开式在圆域 |z-z0|<d 内成立.
复变函数与积分变换
Complex Analysis and Integral Transform
定理(泰勒展开定理) 设f(z)在区域D内解析,z0为 D内的一点, d为z0到D的边界上各点的最短距离,则 当|z-z0|<d 时,
复变函数与积分变换
y
Complex Analysis and Integral Transform
a
z0
x
任何解析函数展开成幂级数的结果就是泰勒级数, 因而是唯一的. 利用泰勒展开式, 我们可以直接通过计算系数: 1 (n) cn f ( z0 ) (n 0,1,2,) n! 把 f (z)在z0点展开成幂级数, 称此为直接展开法
1 | RN ( z ) | 2π 1 2π
K

f (z ) n ( z z ) ds 0 n 1 n N (z z 0 )

| f (z ) | z z0 n ds | z z0 | z z0 n N K 1 M n Mq N q 2π r N 0 2π n N r 1 q
按柯西积分公式, 有 且
1 f ( z) 2πi
f (z ) dz , z z K
1 1 1 1 z z (z z0 ) ( z z0 ) z z0 1 z z0 z z0 由于积分变量z 取在圆周K 上, 点z在K的内部,
z z0 ( z z0 ) n 1 所以 1, z z0 z z n 0 (z z0 ) n 1
K
z z z0
复变函数与积分变换
Complex Analysis and Integral Transform
1 f (z ) d z n f ( z) ( z z ) 0 n 1 2 π i ( z z ) n 0 0 K 1 f (z ) n ( z z0 ) d z . n 1 2 π i K n N (z z0 )
复变函数与积分变换
Complex Analysis and Integral Transform
例如, 求 ez 在 z = 0处的泰勒展开式, 由于(ez)(n) = ez, (ez)(n)|z=0 = 1 (n=0,1,2,...) ， 故有
2 z ez 1 z 2!
zn n!