复数的代数形式及运算

授课主题复数代数形式的加减、乘除运算教学目标1．掌握复数的代数形式的加法、减法运算法则，并熟练地进行化简、求值．2．了解复数的代数形式的加法、减法运算的几何意义．3．会进行复数代数形式的乘、除运算．教学内容1．复数的加法与减法．(1)复数的加、减法法则．(a＋b i)＋(c＋d i)＝(a＋c)＋(b＋d)i；(a＋b i)－(c＋d i)＝(a－c)＋(b－d)i.即两个复数相加(减)，就是实部与实部，虚部与虚部分别相加(减)．(2)复数加法的运算律．复数的加法满足交换律、结合律，即对任意z1，z2，z3∈C，有z1＋z2＝z2＋z1，(z1＋z2)＋z3＝z1＋(z2＋z3).2．复数加、减法的几何意义．复数z1，z2对应的向量OZ1→，OZ2→不共线．(1)复数加法的几何意义：复数z1＋z2是以OZ1→，OZ2→为两邻边的平行四边形的对角线OZ→所对应的复数．因此，复数的加法可以按照向量的加法来进行．(2)复数减法的几何意义：复数z1－z2是连结向量OZ1→，OZ2→的终点，并指向被减向量所对应的复数．3．复数乘法运算法则．设z1＝a＋b i，z2＝c＋d i，那么(a＋b i)(c＋d i)＝(ac－bd)＋(bc＋ad)i.4．复数乘法的运算律．对任意复数z1、z2、z3∈C，有交换律z1·z2＝z2·z1结合律(z1·z2)·z3＝z1(z2·z3)乘法对加法的分配律z1(z2＋z3)＝z1z2＋z1z35．复数除法运算法则．a＋b ic＋d i＝(a＋b i)(c－d i)(c＋d i)(c－d i)＝[ac＋b i·(－d i)]＋(bc－ad)ic2＋d2＝(ac＋bd)＋(bc－ad)ic2＋d2＝ac＋bdc2＋d2＋bc－adc2＋d2i.6．共轭复数．(1)设z1＝a＋b i，z2＝a－b i.当两个复数的实部相等、虚部互为相反数时，这两个复数叫做互为共轭复数．虚部不等于0的两个共轭复数也叫做共轭虚数．通常记z的共轭复数为z.(2)z·z＝(a＋b i)(a－b i)＝a2＋b2＝|z|2＝|z|2.题型一复数的加减运算例1计算：(1)(1＋2i)＋(3－4i)－(5＋6i)；(2)5i－[(3＋4i)－(－1＋3i)]；(3)(a＋b i)－(2a－3b i)－3i(a，b∈R)．解析：(1)(1＋2i)＋(3－4i)－(5＋6i)＝(4－2i)－(5＋6i)＝－1－8i.(2)5i－[(3＋4i)－(－1＋3i)]＝5i－(4＋i)＝－4＋4i.(3)(a＋b i)－(2a－3b i)－3i＝(a－2a)＋[b－(－3b)－3]i＝－a＋(4b－3)i.点评：复数加减运算法则的记忆：①复数的实部与实部相加减，虚部与虚部相加减，加减运算的结果还是一个复数；②把i看作一个字母，类比多项式加减中的合并同类项．巩 固 计算：(1)(－1＋3i)＋(3－23i)；(2)⎝⎛⎭⎫22＋22i －⎝⎛⎭⎫－22＋22i －⎝⎛⎭⎫－22－22i ； (3)[](2－3i )－(a －b )i ＋(a ＋b )i.解析：(1)(－1＋3i)＋(3－23i)＝－1＋3＋(3－23)i ＝2－3i.(2)⎝⎛⎭⎫22＋22i －⎝⎛⎭⎫－22＋22i －⎝⎛⎭⎫－22－22i ＝⎝⎛⎭⎫22＋22＋22＋⎝⎛⎭⎫22－22＋22i ＝322＋22i. (3)[](2－3i )－(a －b )i ＋(a ＋b )i ＝2－3i ＋[]－(a －b )＋(a ＋b )i ＝2＋(2b －3)i.题型二 复数加减运算的几何意义例2 已知平行四边形OABC 的三个顶点O ，A ，C 对应的复数分别为0,3＋2i ，－2＋4i ，试求：(1)AO →表示的复数；(2)CA →表示的复数；(3)求点B 对应的复数．解析：(1)AO →＝－OA →，所以AO →表示的复数为－(3＋2i)，即－3－2i.(2)CA →＝OA →－OC →，所以CA →表示的复数为(3＋2i)－(－2＋4i)＝5－2i.(3)OB →＝OA →＋AB →＝OA →＋OC →，所以OB →表示的复数为(3＋2i)＋(－2＋4i)＝1＋6i ，即B 点对应的复数为1＋6i. 点评：利用复数加减法的几何意义解题：①z 1＋z 2的几何意义是以OZ 1→，OZ 2→为邻边的平行四边形OZ 1ZZ 2的对角线OZ →所在向量；②z 1－z 2的几何意义是连接向量OZ 1→，OZ 2→的终点，并指向被减数的向量Z 2Z 1→所对应的复数；③复平面内两点间距离公式：d ＝|z 1－z 2|(其中z 1，z 2是复平面内两点z 1和z 2所对应的复数，d 为z 1和z 2的距离)．巩 固 在复平面内， 复数1＋i 与－1＋3i 分别对应向量OA →和OB →， 其中O 为坐标原点，则||AB →＝______. 解析：AB →＝OB →－OA →＝－2＋2i ，所以|AB →|＝2 2.答案：22题型三 复数的模相关的运算例3 已知复数z 满足z ＋|z|＝2＋8i ，求复数z.解析：解法一 设z ＝a ＋b i (a ，b ∈R)，则|z |＝a 2＋b 2，代入方程得a ＋b i ＋a 2＋b 2＝2＋8i ，∴⎩⎨⎧ a ＋a 2＋b 2＝2，b ＝8.解得⎩⎪⎨⎪⎧a ＝－15，b ＝8.∴z ＝－15＋8i. 解法二 将原式化为z ＝2－|z |＋8i ，∵ |z |∈R ，∴2－|z |是z 的实部，∴|z |＝(2－|z |)2＋82，即|z |2＝68－4|z |＋|z |2.∴|z |＝17.代入z ＝2－|z |＋8i ，得z ＝－15＋8i.点评：复数模的相关运算，主要是根据求模公式或复数相等的充要条件将复数问题化为实数问题来解决．巩 固 已知z 1＝(3x －4y )＋(y －2x )i ，z 2＝(－2x ＋y )＋(x －3y )i ，x ，y为实数，若z 1－z 2＝5－3i ，则|z 1＋z 2|＝______.解析：z 1－z 2＝[](3x －4y )＋(y －2x )i －[](－2x ＋y )＋(x －3y )i＝[](3x －4y )－(－2x ＋y )＋[](y －2x )－(x －3y )i ＝(5x －5y )＋(－3x ＋4y )i ＝5－3i ，所以⎩⎪⎨⎪⎧5x －5y ＝5，－3x ＋4y ＝－3，解得x ＝1，y ＝0. 所以z 1＝3－2i ，z 2＝－2＋i ，则z 1＋z 2＝1－i ，所以|z 1＋z 2|＝|1－i|＝ 2.答案：2题型四 复数的乘法与除法运算例4 计算：(1)(1＋i)(1－i)＋(－1＋i)；(2)⎝⎛⎭⎫－12＋32i ⎝⎛⎭⎫32＋12i (1＋i)； (3)(－2＋3i)÷(1＋2i)；(4)(5－295i)÷(7－35i)．解析：(1)原式＝1－i 2＋(－1＋i)＝2－1＋i ＝1＋i.(2)原式＝⎣⎡⎦⎤⎝⎛⎭⎫－34－34＋⎝⎛⎭⎫34－14i (1＋i)＝⎝⎛⎭⎫－32＋12i (1＋i)＝⎝⎛⎭⎫－32－12＋⎝⎛⎭⎫12－32i ＝－1＋32＋1－32i. (3)原式＝－2＋3i 1＋2i ＝(－2＋3i )(1－2i )(1＋2i )(1－2i )＝(－2＋6)＋(3＋4)i 12＋22＝45＋75i. (4)原式＝5－29 5 i 7－3 5 i ＝(5－29 5 i )(7＋3 5 i )(7－3 5 i )(7＋3 5 i )＝(35＋29×15)＋(155－29×75)i 72＋(35)2＝470－188 5 i 94＝5－2 5 i. 点评：两个复数代数形式的除法运算步骤：①把除式写为分式；②分子、分母同时乘以分母的共轭复数；③对分子、分母分别进行乘法运算；④把运算结果化为复数的代数形式．巩 固 (1)(1＋i)(－1－i)(3＋i)(1＋3i)＝________.(2)已知i 为虚数单位，则复数1－3i 3＋i的共轭复数是________． 解析：(1)(1＋i)(－1－i)(3＋i)(1＋3i)＝－(1＋i)2(3×1＋(3)2i ＋i ＋3i 2)＝－2i ×4i ＝－8i 2＝8.(2)1－3i 3＋i ＝(1－3i )(3－i )(3＋i )(3－i )＝3－i －3×3i ＋3i 29－i 2＝－10i 10＝－i ，所以1－3i 3＋i的共轭复数为i. 答案：(1)8 (2)i题型五 共轭复数的应用例5 已知z ∈C ，z 为z 的共轭复数，若z ·z －3i z ＝1＋3i ，求z .解析：设z ＝a ＋b i(a ，b ∈R)，则z ＝a －b i(a ，b ∈R)，由题意得(a ＋b i)(a －b i)－3i(a －b i)＝1＋3i ，即a 2＋b 2－3b －3a i ＝1＋3i ，则有⎩⎪⎨⎪⎧ a 2＋b 2－3b ＝1，－3a ＝3.解得⎩⎪⎨⎪⎧ a ＝－1，b ＝0或⎩⎪⎨⎪⎧a ＝－1，b ＝3. 所以z ＝－1或z ＝－1＋3i.点评：(1)要熟悉复数的一些常用性质如z z ＝|z |2＝|z |2，z ∈R ⇔z ＝z 等．(2)当已知条件出现复数等式时，常设出复数的代数形式，利用相等复数的充要条件转化为实数问题求解．巩 固 已知z －1z ＋1为纯虚数，且(z ＋1)(z －＋1)＝|z |2，求复数z . 解析：由(z ＋1)(z ＋1)＝|z |2得z ＋z ＝－1，①由z －1z ＋1为纯虚数，得z －1z ＋1＋z －1z ＋1＝0，所以z ·z －1＝0.② 设z ＝a ＋b i ，代入①②，得a ＝－12，a 2＋b 2＝1. 所以a ＝－12，b ＝±32.所以z ＝－12±32i. 答案：z ＝－12±32i 题型六 复数范围内解方程问题例6 已知1＋i 是方程x 2＋bx ＋c ＝0的一个根(b ，c 为实数)．(1)求b ，c 的值；(2)试判断1－i 是否是方程的根．解析：(1)∵1＋i 是方程x 2＋bx ＋c ＝0的一个根，∴(1＋i)2＋b (1＋i)＋c ＝0，即(b ＋c )＋(2＋b )i ＝0.∴⎩⎪⎨⎪⎧b ＋c ＝0，2＋b ＝0.得b ＝－2，c ＝2. ∴b ，c 的值为b ＝－2，c ＝2.(2)∵方程为x 2－2x ＋2＝0，把1－i 代入方程左边，得(1－i)2－2(1－i)＋2＝0，显然方程成立．∴1－i 是方程的根．点评：在复数范围内解一元二次方程ax 2＋bx ＋c ＝0(a ≠0，a ，b ，c ∈R)，将根设为m ＋n i ，再利用复数相等的充要条件解决问题．巩 固 若复数z 满足方程z 2＋2＝0，则z 3为( )A ．±22B ．－2 2C ．－22iD ．±22i解析：由z 2＋2＝0⇒z ＝±2i ⇒z 3＝±22i ，故选D.答案：D题型七 利用i n 的周期性求解例7 i 是虚数单位，i ＋2i 2＋3i 3＋…＋8i 8＝________(用a ＋b i 的形式表示，a ，b ∈R)．分析：利用i 的周期性化简求和．解析：i ＋2i 2＋3i 3＋…＋8i 8＝i －2－3i ＋4＋5i －6－7i ＋8＝4－4i.答案：4－4i点评：熟记i 的周期性，即i n ＋i n ＋1＋i n ＋2＋i n ＋3＝0(n ∈N *)．记住以下结果，可提高运算速度：①(1＋i)2＝2i ，(1－i)2＝－2i ；②1－i 1＋i ＝－i ，1＋i 1－i＝i ；③1i ＝－i. 巩 固 化简：2＋2i (1－i )2＋⎝ ⎛⎭⎪⎫21＋i 2 014＝____________. 解析：2＋2i (1－i )2＋⎝ ⎛⎭⎪⎫21＋i 2 014＝2(1＋i )－2i ＋⎝⎛⎭⎫22i 1 007＝i(1＋i)＋(－i)1 007＝i ＋i 2＋(－1)1 007×i 1 007 ＝i －1－i 4×251＋3＝i －1－i 3＝－1＋2i.答案：－1＋2i（加减）A 组1．a ，b 为实数，设z 1＝2＋b i ，z 2＝a ＋i ，当z 1＋z 2＝0时，复数a ＋b i 为( )A ．1＋iB ．2＋iC ．3D ．－2－i答案：D2．|(3＋2i)－(4－i)|等于( )A.58B.10 C ．2 D ．－1＋3i解析：|(3＋2i)－(4－i)|＝|－1＋3i|＝(－1)2＋32.故选B.答案：B3．在复平面内，复数6＋5i ，－2＋3i 对应的点分别为A ，B .若C 为线段AB 的中点，则点C 对应的复数是( )A ．4＋8iB ．8＋2iC ．2＋4iD ．4＋i答案：CB 组一、选择题1．已知复数z 1＝2＋i, z 2＝1＋2i, 则复数z ＝z 2－z 1在复平面内对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案：B2．复平面内两点Z 1和Z 2分别对应于复数3＋4i 和5－2i ，那么向量Z 1Z 2→对应的复数为( )A ．3＋4iB ．5－2iC ．－2＋6iD ．2－6i答案：D3．若x 是纯虚数，y 是实数，且2x －1＋i ＝y －(3－y )i ，则x ＋y 等于( )A ．1＋52iB ．－1＋52i C ．1－52i D ．－1－52i 解析：设x ＝a i(a ∈R)，原方程化为2a i －1＋i ＝y －(3－y )i ，即－1＋(2a ＋1)i ＝ y －(3－y )i ，得 －1＝y, 2a ＋1＝－(3－y )．解得 a ＝－52，y ＝－1，选D. 4．满足条件|z －i |＝|3＋4i|的复数z 在复平面上对应点的轨迹是( )A ．一条直线B ．两条直线C ．圆D ．椭圆解析：因为|3＋4i|＝32＋42＝5，所以|z －i|＝5，设z ＝x ＋y i(x ，y ∈R)，则有x 2＋(y －1)2＝5，即x 2＋(y －1)2＝25.故选C.答案：C5．复数z 1＝1＋icos θ，z 2＝sin θ－i ，则|z 1－z 2|的最大值为( )A ．3－2 2 B.2－1 C ．3＋2 2 D.2＋1解析：|z 1－z 2|＝|(1＋icos θ)－(sin θ－i)|＝(1－sin θ)2＋(1＋cos θ)2＝3－2(sin θ－cos θ)＝3＋22sin (θ－π4)≤3＋22＝2＋1.故选D. 答案：D二、填空题6．若复数z 1＋z 2＝3＋4i ，z 1－z 2＝5－2i ，则z 1＝__________.答案：4＋i7．已知|z |＝5，且z －2＋4i 为纯虚数，则复数z ＝________.解析：设z ＝x ＋y i(x ，y ∈R)，则z －2＋4i ＝(x －2)＋(y ＋4)i.由题意知⎩⎪⎨⎪⎧ x －2＝0，y ＋4≠0，x 2＋y 2＝5，得⎩⎪⎨⎪⎧ x ＝2，y ＝1或⎩⎪⎨⎪⎧x ＝2，y ＝－1.所以z ＝2±i. 答案：2±i 8．如图，平行四边形顶点A ，B ，C 所对应的复数分别为i,1,4＋2i(A ，B ，C ，D 按逆时针方向排列)．(1)向量BA →对应的复数为____________；答案：－1＋i(2)向量BC →对应的复数为____________；答案：3＋2i(3)向量BD →对应的复数为____________；答案：2＋3i(4)点D 坐标是____________．答案：(3,3)三、解答题9．设f (z )＝z －3i ＋|z |，若z 1＝－2＋4i ，z 2＝5－i ，求f (z 1＋z 2)的值．解析：因为z 1＝－2＋4i ，z 2＝5－i ，所以z 1＋z 2＝(－2＋4i)＋(5－i)＝3＋3i.于是f (z 1＋z 2)＝f (3＋3i)＝(3＋3i)－3i ＋|3＋3i|＝3＋3 2.10．在复平面内，复数－3－i 与5＋i 对应的向量分别是OA →与OB →，其中O 是原点，求向量OA →＋OB →，BA →对应的复数及A ，B 两点间的距离．解析：向量OA →＋OB →对应的复数为(－3－i)＋(5＋i)＝2.∵BA →＝OA →－OB →，∴向量BA →对应的复数为(－3－i)－(5＋i)＝－8－2i.∴A ，B 两点间的距离为|－8－2i|＝(－8)2＋(－2)2＝217.（乘除）A 组1．设复数满足(1－i)z ＝2i ，则z ＝( )A ．－1＋iB ．－1－iC ．1＋iD ．1－i解析：z ＝2i 1－i ＝2i (1＋i )(1－i )(1＋i )＝－1＋i.故选A.答案：A2．已知z 1＋i＝2＋i ，则复数z ＝( ) A ．－1－3i B ．1－3iC ．3＋iD ．3－i解析：由题意知z ＝(2＋i)(1＋i)＝1＋3i ，∴z ＝1－3i.答案：B3．复数2i 1＋i(i 是虚数单位)的虚部是( ) A ．1 B ．－1 C ．i D ．－i答案：AB 组一、选择题1．(2013·广东卷)若复数z 满足i z ＝2＋4i ，则在复平面内，z 对应的点的坐标是( )A ．(2,4)B ．(2，－4) C. (4，－2) D ．(4,2)解析：z ＝2＋4i i＝4－2i 对应的点的坐标是(4，－2)，故选C. 答案：C2．(2013·山东卷)若复数z 满足(z －3)(2－i)＝5(i 为虚数单位)，则z 的共轭复数z －为( )A ．2＋iB ．2－iC ．5＋iD ．5－i解析：由(z －3)(2－i)＝5得，z －3＝52－i＝2＋i ，所以 z ＝5＋i ，所以z ＝5－i.故选D. 答案：D3．设a ，b ，c ，d ∈R ，则复数(a ＋b i)(c ＋d i)为实数的充要条件是( )A ．ad －bc ＝0B ．ac －bd ＝0C ．ac ＋bd ＝0D ．ad ＋bc ＝0解析：a ，b ，c ，d ∈R ，复数(a ＋b i)(c ＋d i)＝(ac －bd )＋(ad ＋bc )i 为实数，∴ad ＋bc ＝0，选D.答案：D4．已知复数z ＝1＋i ，则z ＋1z2＝( ) A.12－i B.12＋i C ．－12－i D ．－12＋i 答案：A二、填空题5．设复数z 满足z (2－3i)＝6＋4i(其中i 为虚数单位)，则z 的模为________．解析：z (2－3i)＝2(3＋2i)，2－3i 与3＋2i 的模相等，z 的模为2.答案：26．(2013·重庆卷)已知复数z ＝5i 1＋2i(是虚数单位)，则|z |＝________________. 解析：|z |＝⎪⎪⎪⎪5i 1＋2i ＝55＝ 5. 答案： 57. 设i 是虚数单位，复数1＋a i 2－i为纯虚数，则实数a ＝_________________. 解析：1＋a i 2－i ＝1＋a i 2－i ·2＋i 2＋i ＝2－a ＋(2a ＋1)i 5，因为1＋a i 2－i 为纯虚数，所以⎩⎪⎨⎪⎧2－a ＝0，2a ＋1≠0，所以a ＝2. 答案：28．若复数z 满足|z |－z －＝101－2i，则z ＝________. 解析：设z ＝a ＋b i(a ，b ∈R)，则有a 2＋b 2－a ＋b i ＝2＋4i.所以⎩⎨⎧a 2＋b 2－a ＝2，b ＝4，得a ＝3，b ＝4. 所以z ＝3＋4i.答案：3＋4i三、解答题9．已知复数3z －z －对应的点落在射线y ＝－x (x ≤0)上，|z ＋1|＝2，求复数z .解析：设z ＝a ＋b i(a ，b ∈R)，则3z －z ＝3a ＋3b i －a ＋b i ＝2a ＋4b i ，由题意得⎩⎪⎨⎪⎧4b ＝－2a ，b ＞0.① 又由|z ＋1|＝2，得(a ＋1)2＋b 2＝2，②由①，②解得⎩⎪⎨⎪⎧a ＝－2，b ＝1，所以z ＝－2＋i. 10. 复数z ＝(1＋i )3(a ＋b i )1－i且|z |＝4，z 对应的点在第一象限内，若复数0，z ，z －对应的点是正三角形的三个顶点，求实数a ，b 的值．解析：z ＝(1＋i )2(1＋i )(a ＋b i )1－i＝2i·i(a ＋b i)＝－2a －2b i. 由|z |＝4，得a 2＋b 2＝4.①因为复数0，z ，z 对应的点是正三角形的三个顶点，所以|z |＝|z －z |，把z ＝－2a －2b i 代入化简，得|b |＝1.② 又因为z 点在第一象限内，所以a ＜0，b ＜0.由①②，得⎩⎨⎧a ＝－3，b ＝－1.故所求a ＝－3，b ＝－1.。

数学中的复数运算应用技巧复数是数学中一种重要的概念，它在工程学、物理学等领域中有着广泛的应用。

复数的运算是复数应用的基础，下面将介绍一些数学中常见的复数运算应用技巧。

一、复数的表示方式复数通常表示为a+bi的形式，其中a为实部，bi为虚部，i为虚数单位。

实数部分和虚数部分都可以是任意实数。

复数的表示方式有两种常用形式：代数形式和极坐标形式。

代数形式：复数a+bi表示一个平面上的点，横坐标为a，纵坐标为b。

极坐标形式：复数r(cosθ+isinθ)表示一个和原点的距离为r、与x轴正方向的夹角为θ的极坐标点。

二、复数的四则运算复数的四则运算与实数的四则运算类似，但要注意虚部的运算。

下面分别介绍加法、减法、乘法和除法的运算规则。

1. 加法：将两个复数的实部相加，虚部相加，得到新的复数。

例如，对于复数a+bi和c+di的相加，结果为(a+c)+(b+d)i。

2. 减法：将两个复数的实部相减，虚部相减，得到新的复数。

例如，对于复数a+bi和c+di的相减，结果为(a-c)+(b-d)i。

3. 乘法：将两个复数进行分配律展开计算。

例如，对于复数a+bi和c+di的相乘，结果为(ac-bd)+(ad+bc)i。

4. 除法：将两个复数的乘法结果与除数的平方和进行除法运算。

例如，对于复数a+bi和c+di的相除，结果为((ac+bd)/(c^2+d^2))+((bc-ad)/(c^2+d^2))i。

三、复数运算的应用技巧1. 求模和共轭：复数的模表示复数到原点的距离，并且模的平方等于复数乘以共轭的结果。

例如，对于复数a+bi，其模为√(a^2+b^2)。

共轭复数表示将复数的虚部取相反数得到的新的复数。

例如，对于复数a+bi，其共轭复数为a-bi。

2. 约简运算：对于复数的乘法和除法，可以将复数分别写成代数形式和极坐标形式进行运算，最后再转换回代数形式。

例如，对于复数a+bi和c+di的相乘，可以先将其转换成极坐标形式，即r(cosθ+isinθ)，再进行乘法运算，最后再转换回代数形式。

复数的代数形式及其运算第85课时课题：复数的代数形式及其运算一．教学目标：掌握复数的基本题型，主要是讨论复数的概念,复数相等,复数的几何表示,计算复数模，共轭复数，解复数方程等。

二．教学重点：复数的几何表示，计算复数模，共轭复数,解复数方程等。

三．教学过程:（一）主要知识：1．共轭复数规律，；2．复数的代数运算规律(1）i=1，i=i,i=1，i=i;(3)i・i・i・i=1，i＋i＋i＋i=0；；3．辐角的运算规律(1)Arg（z・z）＝Argz＋Argz（3）Arg=nAr gz(n∈N）.。

.，n1.或z∈R。

要条件是|z|＝|a|.（6）z・z≠0,则4．根的规律：复系数一元n次方程有且只有n个根，实系数一元n次方程的虚根成对共轭出现。

5．求最值时，除了代数、三角的常规方法外，还需注意几何法及不等式||z｜|z｜｜≤｜z±z｜≤｜z｜+|z|的运用.即｜z±z｜≤｜z|+|z|等号成立的条件是：z，z所对应的向量共线且同向。

|z±z|≥|z|｜z|等号成立的条件是：z,z所对立的向量共线且异向。

（二）范例分析Ⅰ.2004年高考数学题选1.(2004高考数学试题(浙江卷,6)）已知复数z1=3+4i, z2=t+i，且是实数，则实数t=（）A．B．C．?D．？2。

(2004年北京春季卷,2)当时，复数在复平面上对应的点位于（）A．第一象限B．第二象限 C．第三象限D．第四象限3.(2004年北京卷，2）满足条件的复数在复平面上对应点的轨迹是（ C ) A．一条直线B．两条直线C．圆D．椭圆Ⅱ.主要的思想方法和典型例题分析：1．化归思想复数的代数、几何、向量及三角表示，把复数与实数、三角、平面几何和解析几何有机地联系在一起，这就保证了可将复数问题化归为实数、三角、几何问题。

反之亦然。

这种化归的思想方法应贯穿复数的始终。

【分析】这是解答题，由于出现了复数和，宜统一形式,正面求解。

复数及其运算复数是数学中的一个重要概念，它在代数和几何中都扮演着重要的角色。

本文将对复数的定义、运算法则以及复数的性质做出详细的解释和说明。

一、复数的定义复数由实部和虚部组成，可以用a+bi的形式表示，其中a是实部，b是虚部，i是虚数单位，满足i²=-1。

实部和虚部都可以是实数。

二、复数的运算法则1. 加法法则：复数的加法满足交换律和结合律，即(a+bi)+(c+di)=(a+c)+(b+d)i。

2. 减法法则：复数的减法满足减法的定义，即(a+bi)-(c+di)=(a-c)+(b-d)i。

3. 乘法法则：复数的乘法按照分配律和乘法公式进行，即(a+bi)(c+di)=(ac-bd)+(ad+bc)i。

4. 除法法则：复数的除法要利用到共轭复数的概念，即(a+bi)/(c+di)=(ac+bd)/(c²+d²)+((bc-ad)/(c²+d²))i。

三、复数的性质1. 共轭复数：一个复数的共轭复数是指虚部符号变反，即(a+bi)的共轭复数为(a-bi)。

2. 模：复数的模是指其到原点的距离，在复平面中可以用勾股定理得到。

对于复数a+bi，其模为根号下(a²+b²)。

3. 平方根：复数的平方根可以通过求解二次方程来得到。

对于复数a+bi，其平方根为±根号下[(根号下(a²+b²)+a)/2]+[(根号下(a²+b²)-a)/2]i。

4. 范数：复数的范数是指其模的平方，也就是模的平方根。

对于复数a+bi，其范数为a²+b²。

综上所述，复数是由实部和虚部组成的数，并且复数的运算遵循特定的法则。

复数的共轭、模、平方根和范数等概念对于理解和应用复数有着重要的作用。

在代数和几何的研究中，复数的运算与复平面的结构密切相关，大大拓展了数学的领域。

通过学习复数及其运算法则，可以帮助我们更好地理解和解决涉及到复数的问题，如解方程、计算向量等。

复数的各类表达形式一、代数形式表示形式：表示一个复数复数有多种表示形式，常用形式z=a+bi 叫做代数形式。

二、几何形式点的表示形式：表示复平满的一个点在直角坐标系中，以x为实轴，y为虚轴，O为原点形成的坐标系叫做复平面，这样所有复数都可以复平面上的点表示被唯一确定。

复数z=a+bi 用复平面上的点z(a，b )表示。

这种形式使复数的问题可以借助图形来研究。

也可反过来用复数的理论解决一些几何问题。

三、三角形式表示形式复数z＝a+bi化为三角形式，z＝r(cosθ+sinθi)。

式中r=∣z∣=√(a^2+b^2)，是复数的模(即绝对值)；θ是以x轴为始边，射线OZ为终边的角，叫做复数的辐角，记作argz，即argz=θ=arctan(b/a)。

这种形式便于作复数的乘、除、乘方、开方运算。

四、指数形式表示形式将复数的三角形式z＝r( cosθ+isinθ)中的cosθ+isinθ换为exp(iθ)，复数就表为指数形式z＝rexp(iθ)。

向量在数学与物理中，既有大小又有方向的量叫做向量〔亦称矢量〕，在数学中与之相对的是数量，在物理中与之相对的是标量。

向量的运算法那么1、向量的加法向量的加法满足平行四边形法那么和三角形法那么。

OB+OA=OC。

a+b=(x+x'，y+y')。

a+0=0+a=a。

向量加法的运算律：交换律：a+b=b+a；结合律：(a+b)+c=a+(b+c)。

2、向量的减法如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0. 0的反向量为0AB-AC=CB. 即“共同起点，指向被减〞a=(x,y)b=(x',y') 那么a-b=(x-x',y-y').如图：c=a-b 以b的结束为起点，a的结束为终点。

3、数乘向量实数λ和向量a的乘积是一个向量，记作λa，且∣λa∣=∣λ∣·∣a∣。

当λ>0时，λa与a同方向当λ<0时，λa与a反方向；当λ=0时，λa=0，方向任意。

复数的代数运算公式一、复数的定义复数是由实数和虚数构成的数，可以表示为 a+bi 的形式，其中 a 和 b 分别为实部和虚部，i 是虚数单位，满足 i^2 = -1。

二、复数的加法对于两个复数 a+bi 和 c+di，它们的加法运算可以用以下公式表示：(a+bi) + (c+di) = (a+c) + (b+d)i三、复数的减法对于两个复数 a+bi 和 c+di，它们的减法运算可以用以下公式表示：(a+bi) - (c+di) = (a-c) + (b-d)i四、复数的乘法对于两个复数 a+bi 和 c+di，它们的乘法运算可以用以下公式表示：(a+bi) * (c+di) = (ac-bd) + (ad+bc)i五、复数的除法对于两个复数 a+bi 和 c+di，它们的除法运算可以用以下公式表示：(a+bi) / (c+di) = [(ac+bd)/(c^2+d^2)] + [(bc-ad)/(c^2+d^2)]i六、复数的共轭对于一个复数 a+bi，它的共轭可以用以下公式表示：(a+bi)的共轭 = (a-bi)七、复数的模对于一个复数 a+bi，它的模可以用以下公式表示：|a+bi| = √(a^2+b^2)八、复数的幂运算对于一个复数 a+bi 和一个整数 n，它们的幂运算可以用以下公式表示：(a+bi)^n = (a^2+b^2)^(n/2) * cos(nθ) + (a^2+b^2)^(n/2) * sin(nθ)i九、复数的指数函数对于一个复数 a+bi，它的指数函数可以用以下公式表示：e^(a+bi) = e^a * cos(b) + e^a * sin(b)i十、复数的对数函数对于一个复数 a+bi，它的对数函数可以用以下公式表示：ln(a+bi) = ln|a+bi| + i * arg(a+bi)复数的代数运算公式包括加法、减法、乘法、除法、共轭、模、幂运算、指数函数和对数函数等。

复数基础知识及其运算规律一、复数的概念1.复数的定义：复数是由实数和虚数构成的数，一般形式为a+bi，其中a和b分别为实数，i为虚数单位，满足i^2=-1。

2.复数的分类：a)纯虚数：实部为0的复数，如i、-i等；b)实数：虚部为0的复数，如2、-3等；c)混合数：实部和虚部都不为0的复数，如1+2i、-3-4i等。

二、复数的表示方法1.代数表示法：用a+bi的形式表示复数；2.极坐标表示法：用r(cosθ+isinθ)的形式表示复数，其中r为模长，θ为辐角。

三、复数的运算规律1.加减法：a)(a+bi) + (c+di) = (a+c) + (b+d)i；b)(a+bi) - (c+di) = (a-c) + (b-d)i。

c)(a+bi)(c+di) = (ac-bd) + (ad+bc)i；d)特殊情形：两个纯虚数相乘，结果为实数；e)单位根的乘法：i^k，其中k为整数。

f)(a+bi)/(c+di) = [(ac+bd)/(c2+d2)] + [(bc-ad)/(c2+d2)]i。

g)(a+bi)^2 = (a2-b2) + 2abi；h)(a+bi)3、(a+bi)4等，可以利用乘方公式进行展开。

2.共轭复数：a)若复数为a+bi，则它的共轭复数为a-bi；b)共轭复数具有以下性质：两数相加为实数，两数相乘为实数。

四、复数的性质1.模长：表示复数在复平面上的长度，公式为|a+bi| = √(a2+b2)；2.辐角：表示复数在复平面上与实轴的夹角，公式为θ = arctan(b/a)，其中a≠0；3.复数的平方等于1的解：i、-1、1+i、1-i等；4.复数的平方等于-1的解：i、-i等；5.复数的平方等于k（k为非零实数）的解：±√k、±i√k等。

五、复数在实际应用中的例子1.信号处理：在通信系统中，信号往往可以表示为复数形式，如调制解调器中的正弦波信号；2.物理学：在电磁学、量子力学等领域，复数用于描述物理量，如电流、电压、波函数等；3.工程学：在电子工程、控制理论等领域，复数用于分析电路、系统稳定性等。

复数代数形式的四则运算【要点梳理】要点一、复数的加减运算1.复数的加法、减法运算法则： 设1z a bi =+，2z c di =+（,,,a b c d R ∈），我们规定：12()()()()z z a bi c di a c b d i +=+++=+++21()()z z c a d b i -=-+-要点诠释：（1）复数加法中的规定是实部与实部相加，虚部与虚部相加，减法同样。

很明显，两个复数的和（差）仍然是一个复数，复数的加（减）法可以推广到多个复数相加（减）的情形．（2）复数的加减法，可模仿多项式的加减法法则计算，不必死记公式。

2.复数的加法运算律:交换律：z 1+z 2=z 2+z 1结合律:：(z 1+z 2)+z 3=z 1+(z 2+z 3)要点二、复数的加减运算的几何意义1. 复数的表示形式：代数形式：z a bi =+（,a b R ∈）几何表示：①坐标表示：在复平面内以点(,)Z a b 表示复数z a bi =+（,a b R ∈）； ②向量表示：以原点O 为起点，点(,)Z a b 为终点的向量OZ 表示复数z a bi =+.要点诠释：复数z a bi =+←−−−→一一对应复平面内的点(,)Z a b ←−−−→一一对应平面向量OZ 2．复数加、减法的几何意义：如果复数1z 、2z 分别对应于向量1OP 、2OP ，那么以1OP 、2OP 为两边作平行四边形12OPSP ，对角线OS 表示的向量OS 就是12z z +的和所对应的向量.对角线21P P 表示的向量21P P 就是两个复数的差12z z -所对应的向量.设复数z 1=a +bi ，z 2=c +di ，在复平面上所对应的向量为1OZ 、2OZ ，即1OZ 、2OZ 的坐标形式为1OZ =(a ，b )，2OZ =(c ，d )以1OZ 、2OZ 为邻边作平行四边形OZ 1ZZ 2，则对角线OZ 对应的向量是OZ ，由于OZ =1OZ +2OZ =(a ，b )+(c ，d )=(a +c ，b +d )，所以1OZ 和2OZ 的和就是与复数(a +c )+(b +d )i对应的向量类似复数加法的几何意义，由于z 1－z 2=(a －c )+(b －d )i ，而向量12Z Z = 1OZ -2OZ =(a ，b )-(c ，d )=(a -c ，b -d )，所以1OZ 和2OZ 的差就是与复数(a －c )+(b －d )i 对应的向量要点诠释：要会运用复数运算的几何意义去解题，它包含两个方面：（1）利用几何意义可以把几何图形的变 换转化成复数运算去处理（2）反过来，对于一些复数运算式也可以给以几何解释，使复数做为工具运用于几何之中。

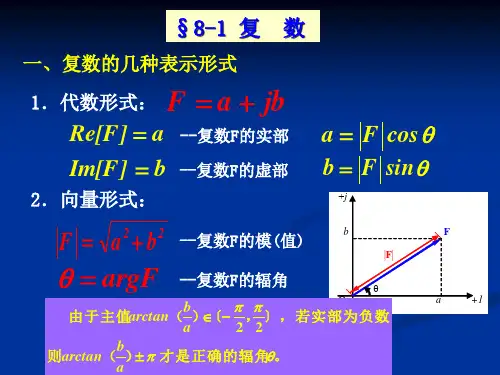
复数的运算法则1.复数的表示形式（1）代数形式共轭复数F*=a-jb在数学中虚单位常用i表示，如F=a+bi，但由于在电路中已用i表示电流，故虚单位改用j表示。

实部(real part)：Re[F] = a；虚部(imaginary part)：Im[F] = b。

复数可用复平面上的向量表示(如图所示)。

（2）三角形式F=|F|(cosθ+jsinθ)|F|为复数的模，θ为复数的幅角，θ=argF。

则|F|=θ=arctan(b/a)。

且a=|F|cosθ，b=|F|sinθ 。

（3）指数形式(exponential form)（4）极坐标形式(polar form)F=|F|&lt;θ2.复数的基本运算（1）加减运算复数的加减运算采用代数形式较为简便，或在复平面中使用平行四边形法则。

设F1 = a1 + jb1，F2 = a2 + jb2，有平行四边形法则：（2）乘除运算复数的乘除运算使用指数形式或极坐标形式较为简便。

①指数形式即复数乘积的模等于各复数模的积；辐角等于各复数辐角的和。

②极坐标形式（3）旋转因子复数ejθ = cosθ + jsinθ = 1∠θFejθ →复数F逆时针旋转一个角度θ ，模不变+j ，–j，-1 都可以看成旋转因子。

若一个复数乘以j，等于在复平面上把该复数逆时针旋转π/2。

若一个复数除以j ，等于把该复数乘以-j ，则等于在复平面上把该复数顺时针旋转π/2。

（4）相等运算两个复数相等必须满足：复数的实部、虚部分别对应相等；或者复数的模和辐角分别对应相等。

若F1 = F2，则必须有或。