下载文档原格式
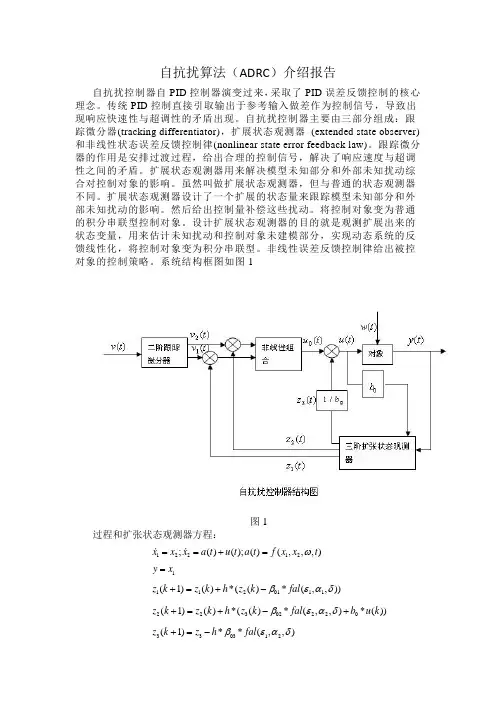
自抗扰算法（ADRC ）介绍报告自抗扰控制器自PID 控制器演变过来，采取了PID 误差反馈控制的核心理念。
传统PID 控制直接引取输出于参考输入做差作为控制信号，导致出现响应快速性与超调性的矛盾出现。
自抗扰控制器主要由三部分组成：跟踪微分器(tracking differentiator)，扩展状态观测器 (extended state observer) 和非线性状态误差反馈控制律(nonlinear state error feedback law)。
跟踪微分器的作用是安排过渡过程，给出合理的控制信号，解决了响应速度与超调性之间的矛盾。
扩展状态观测器用来解决模型未知部分和外部未知扰动综合对控制对象的影响。
虽然叫做扩展状态观测器，但与普通的状态观测器不同。
扩展状态观测器设计了一个扩展的状态量来跟踪模型未知部分和外部未知扰动的影响。
然后给出控制量补偿这些扰动。
将控制对象变为普通的积分串联型控制对象。
设计扩展状态观测器的目的就是观测扩展出来的状态变量，用来估计未知扰动和控制对象未建模部分，实现动态系统的反馈线性化，将控制对象变为积分串联型。
非线性误差反馈控制律给出被控对象的控制策略。
系统结构框图如图1图1过程和扩张状态观测器方程：1y x =22302220(1)()*(()*(,,)*())z k z k h z k fal b u k βεαδ+=+-+1120111(1)()*(()*(,,))z k z k h z k fal βεαδ+=+-12212;()();()(,,,)x x x a t u t a t f x x t ω==+=330312(1)**(,,)z k z h fal βεαδ+=-非线性控制策略方程：二阶微分控制器：112(1)()*()v k v k h v k +=+2212(1)()*(()(),(),,)v k v k h fhan v k v k v k r h +=+-其中，h 为积分步长，r 为跟踪算子。
国家精品课程/ 国家精品资源共享课程/ 国家级精品教材国家级十一(二)五规划教材/ 教育部自动化专业教学指导委员会牵头规划系列教材控制系统仿真与CAD第十章智能控制器设计方法自抗扰控制Auto Disturbances Rejection Control主讲：薛定宇教授自抗扰控制自抗扰控制199x年有韩京清研究员提出的控制策略 控制器设计时无需受控对象模型的参数 有三个组成部分微分跟踪器扩张状态观测器自抗扰控制器微分跟踪器 数学模型S-函数(状态方程)的实现 S-函数入口语句S-函数的基本框架扩张的状态观测器 数学模型其中扩张状态观测器的S-函数实现选择参数，设计状态观测器主函数 输入输出路数、连续离散状态变量个数扩张状态观测器支持函数自抗扰控制器数学模型其中方程没有连续、离散状态输入信号为m(t)=[v(t), v2(t), z1(t), z2(t), z3(t)]1输出信号为u(t)自抗扰控制器S-函数实现 主函数支持函数 输入信号为 m (t )=[v 1(t ), v 2(t ), z 1(t ), z 2(t ), z 3(t )]输出信号为 u (t )例10-4自抗扰控制器仿真 时变受控对象模型搭建仿真框图 ex_han2.slx控制器参数仿真模型 受控对象ADRC控制器模块封装 自抗扰控制器内部结构自抗扰控制器仿真 新的系统框图控制器参数选择自抗扰控制设计小结 自抗扰控制的三个组成部分 微分跟踪器扩张的状态观测器自抗扰控制器数学模型与S-函数实现自抗扰控制系统的仿真与设计。
3.3自抗扰控制技术旳MATLAB仿真自抗扰控制技术是由韩京清专家根据数年实际控制工程经验提出旳新旳控制理论。
在老式旳工业和其他控制领域，PID一直占据主导地位。
目前，PID 在航空航天、运动控制及其他过程控制领域，仍然占据90%以上旳份额。
不过，PID自身还是存在缺陷，而韩京清专家正是出于对P1D控制算法旳充足认知，尤其是对其缺陷旳清晰分析，提出了自抗扰控制技术。
3.3.1自抗扰控制技术概述自抗扰控制技术旳提出是根据对PID控制技术旳充足认知，扬其长处，抑其缺陷而提出旳。
老式PID控制技术应用领域很广泛，其控制构造如图3-9所示。
图3-9 老式PID构造其中，•++⎰=ekekdeku t21)(ττ。
众所周知，PID控制原理是基于误差来生成消除误差控制方略:用误差旳过去、目前和变化趋势旳加权和消除误差。
其长处有:靠控制目旳与实际行为之间旳误差来确定消除此误差旳控制方略，而不是靠被控对象旳“输入一输出”关系，即不靠被控对象旳“输入-输出”模型来决定控制方略，简朴易行，只要选择PID增益使闭环稳定，就能使对象到达静态指标。
当然PID控制仍有缺陷，其缺陷如下1、采用PID校正系统闭环动态品质对PID增益旳交化太敏感，当被控对象处在变化旳环境中时，根据环境旳变化常常需要变动PID旳增益。
2、“基于误差反馈消除误差”是PID控制技术旳精髓，但实际状况中直接取目旳与实际行为之间旳误差常常会使初始控制力太大而使系统行为出现超调，而这正是导致使用PID控制技术旳闭环系统产生“迅速性”和“超调”不可调和矛盾旳重要原因。
3、PID是用误差旳比例、积分、微分旳加权和形式来形成反馈控制量旳，然而在诸多场所下，由于没有合适旳微分器，一般采用PI控制规律，限制了PID旳控制能力。
4、PID是用误差旳过去、目前和未来旳合适组合来产生程制量旳。
经典PID一般采用线性取和措施，不过实际系统多为非线性系统，因此非线性拉制器更适合实际状况。
自抗扰控制技术简介1．自抗扰控制技术概述1.1 什么是自抗扰控制技术自抗扰控制器（Auto/Active Disturbances Rejection Controler，ADRC）技术，是发扬PID控制技术的精髓并吸取现代控制理论的成就，运用计算机仿真实验结果的归纳和总结和综合中探索而来的，是不依赖被控对象精确模型的、能够替代PID控制技术的、新型实用数字控制技术。
1.2 自抗扰控制技术的提出者——韩京清韩京清，朝鲜族, 1937生，系统与控制专家，中国科学院数学与系统科学研究院系统科学研究所研究员、博士生导师,长期从事控制理论与应用研究工作，是我国控制理论和应用早期开拓者之一。
韩京清先生于1998年正式提出自抗扰控制这一思想。
在这个思想提出之后，国内外许多研究者都围绕着“自抗扰控制”展开实际工程应用的研究。
同时，自抗扰控制的理论分析的研究也在不断的深入。
1.3 自抗扰控制技术的特点和优点（1）自抗扰控制器采用“观测＋补偿”的方法来处理控制系统中的非线性与不确定性，同时配合非线性的反馈方式，提高控制器的动态性能。
（2）自抗扰控制器算法简单、易于实现、精度高、速度快、抗扰能力强。
（3）统一处理确定系统和不确定系统的控制问题；扰动抑制不需外扰模型或者外扰是否观测；控制算法不需辨识控制对象；统一处理非线性和线性系统；可以进行时滞系统控制；解耦控制只要考虑静态耦合，不用考虑动态耦合等。
2．自抗扰控制技术提出的背景2.1 现代控制理论的缺点和改进现代控制理论以状态变量描述为基础，以状态反馈实现极点配置来改善全局动态特性的问题。
因而，此种控制的主要手段是状态反馈。
“这种全局控制方法需要知道关于开环动态特性的先验知识和状态变量的信息，这在许多工程实际中是很不现实的，因为工程实际提供不了有关开环动态特性的多少先念知识，因此这种全局控制方法是很难在实际中得到应用。
”这就是现代控制理论的缺点，这也限制了这种控制方法在工程实际中的应用。
目录目录目录 (1)1 绪论 (1)2 问题描述 (1)3 发展现状 (2)3.1 非线性跟踪微分器 (2)3.2 扩张状态观测器 (3)3.3 自抗扰控制律 (4)3.4 参数整定问题 (4)4 未来展望 (15分) (4)5 结论 (5)参考文献 (6)1 绪论自抗扰控制是韩京清先生以对控制理论的反思为开端提出的以反馈系统的标准型（积分器串联型）为基础，以工程控制的鲁棒性为目标的控制技术[1-5]。
其思想是以工业界占主导地位的PID控制为出发点，在改进非线性PID的基础上提出自抗扰的概念，算法简单，在未知强非线性和不确定强扰动的作用下仍能够保持控制精度。
在国内，自抗扰控制技术在四旋翼无人机控制[6]、航天器姿态控制[7]、精密车床中快速刀具的伺服控制[8]、电机的励磁控制[9]等方面均有应用案例。
在国外，自抗扰控制于2009年通过了运动控制的工业评估[10]；2013年，德州仪器开始在全球发布以自抗扰为技术核心的运动控制芯片[11]。
可见，自抗扰控制技术具备巨大的潜力与工程应用前景。
2 问题描述1989年，韩京清先生提出了对控制领域的疑问——模型论还是控制论。
模型论“靠系统的数学模型去找控制率”，后者依靠的是系统的“某些响应特征或过程的某些实时信息”。
而“通过误差来消除误差”正是简单的线性PID所蕴含的朴素思想，也是PID能够在工业界获得广泛应用的原因。
而以现代控制理论为代表的控制理论虽然在数学上严密可证，然而在实际应用中却较少，因为实际的控制对象总是不可避免地存在未知与不确定性。
因此，反思控制理论数学化带来的理论与工业实践的脱节，探索新的控制技术与理论是有必要的。
而自抗扰控制技术就是基于以上的问题，以PID为出发点，探索控制技术与理论的新方向。
3 发展现状3.1 非线性跟踪微分器自抗扰控制目前主要包括三方面的内容：非线性跟踪微分器，扩张状态观测器以及一系列自抗扰控制律的设计。
非线性跟踪微分器能够抑制噪声信号的放大效应，得到较好的微分近似信号。
自抗扰控制技术介绍1．自抗扰控制技术概述1.1 什么是自抗扰控制技术自抗扰控制器（Auto/Active Disturbances Rejection Controler, ADRC）技术, 是发扬PID控制技术精髓并吸收现代控制理论成就, 利用计算机仿真试验结果归纳和总结和综合中探索而来, 是不依靠被控对象正确模型、能够替换PID控制技术、新型实用数字控制技术。
1.2 自抗扰控制技术提出者——韩京清韩京清, 朝鲜族, 1937生, 系统与控制教授, 中国科学院数学与系统科学研究院系统科学研究所研究员、博士生导师,长久从事控制理论与应用研究工作, 是中国控制理论和应用早期开拓者之一。
韩京清先生于1998年正式提出自抗扰控制这一思想。
在这个思想提出以后, 中国外很多研究者都围绕着“自抗扰控制”展开实际工程应用研究。
同时, 自抗扰控制理论分析研究也在不停深入。
1.3 自抗扰控制技术特点和优点（1）自抗扰控制器采取“观察＋赔偿”方法来处理控制系统中非线性与不确定性, 同时配合非线性反馈方法, 提升控制器动态性能。
（2）自抗扰控制器算法简单、易于实现、精度高、速度快、抗扰能力强。
（3）统一处理确定系统和不确定系统控制问题; 扰动抑制不需外扰模型或者外扰是否观察; 控制算法不需辨识控制对象; 统一处理非线性和线性系统; 能够进行时滞系统控制; 解耦控制只要考虑静态耦合, 不用考虑动态耦合等。
2．自抗扰控制技术提出背景2.1 现代控制理论缺点和改善现代控制理论以状态变量描述为基础, 以状态反馈实现极点配置来改善全局动态特征问题。
所以, 此种控制关键手段是状态反馈。
“这种全局控制方法需要知道相关开环动态特征先验知识和状态变量信息, 这在很多工程实际中是很不现实, 因为工程实际提供不了相关开环动态特征多少先念知识, 所以这种全局控制方法是极难在实际中得到应用。
”这就是现代控制理论缺点, 这也限制了这种控制方法在工程实际中应用。
从PID技术到“自抗扰控制”技术韩京清(中国科学院数学与系统科学研究院系统科学所，北京100080)摘要:从传统PID的原理出发，分析了它的优缺点。
利用非线性机制来开发了一些具有特殊功能的环节:跟踪微分器CTD)，扩张状态观测器(ESO)，非线性PID(NPID)等，并以此组合出高品质的新型控制器一自抗扰控制器(ADRC )，从而形成了新的“自抗扰控制”技术。
新型的控制器具有算法简单、参数易于调N的特点。
关键词:PID;非线性反馈;自抗扰控制中图分类号:TP 13文献标识码:A1引言PID控制器在工业过程控制中占据的主导地位是绝无仅有的。
目前，PID控制器在运动控制、航天控制及其他过程控制的应用中，仍然占据95%以上。
据最新的文献[1]显示，在纸浆和造纸工业中，PI控制器的应用甚至超过了98%。
由此可见，不管现代控制理论给出的控制方法在理论上是多么的完美而漂亮，可是仍然难以在现代的工业控制中找到白己的立足之处。
这说明时至今日，控制理论和工程实际相脱离的鸿沟不但没有弥合的迹象，反而有了加剧的趋势。
面对这种尴尬的局面，我们不得不重新认识PID控制技术，探索其机理，发扬其优势，克服其缺点，进而寻找更好的控制技术。
本文的出发点就在于此。
2传统PID的结构及优、缺点传统PID的结构如图1所示。
图1传统PID的结构工业过程控制的PID控制原理是基于误差来生成消除误差的控制策略:用误差的过去、现在和变化趋势的加权和控制策略。
PID在实际中大量应用，但不易满足高性能要求，于是想靠对象模型来寻求更好的控制方法，但靠模型的路了恰恰把PID的最大优点丢掉了PID的优点:靠控制目标与实际行为之问的误差来确定消除此误差的控制策略。
PID的缺点:①误差的取法;②由误差e提取deldt的办法;③“加权和”策略不一定最好;①积分反馈有许多副作用。
我们的思路是探讨更好的控制策略，这种策略的宗旨是保留PID的优点，克服其缺点。
我们的工具是利用特殊非线性效应来开发具有特殊功能的环节，并以此来组合出高品质控制器。
克服PID“缺点”的具体办法是:①安排合适的“过渡过程”;②合理提取“微分”一“跟踪微分器”(Tracking Differentiator, TD);③探讨合适的组合方法一“非线性组合”(NF );①探讨“扰动估计”办法一韦、一张状态观测器”(Extended State Observer,ESO)。
下面，我们以二阶对象控制为例来讨论保留PID的优点，克服其缺点的办法。
3合理提取微分的方法一“跟踪微分器”(TD)经典微分器的形式为:式中，、分别是系统的输入、输出信号，是系统的传递函数。
当对信号叠加随机噪声n(t)时:越小时，系统输出的“噪声放大”就越严重。
若用近似微分公式z则有可以降低“噪声放大”的效应。
这里，“微分”信号是用“尽快地跟踪输入号的办法得到的。
那么能否用“最快地跟踪”办法得到微分信号呢?2)跟踪一微分器的一般理论：设二阶系统为:上式的“快速最优控制”综合系统为:把(t)改为(t)一v (t)，得式中，是在限制r下，最快地跟踪输入信号V (t)。
充分接近V (t)时，有(t)可做V (t}的近似微分。
定理设二阶系统为:若二阶系统式(2)稳定，那么对有界可测v (t), tT>0，有系统)且系统式((3)的解f(xi一v(t)，x2/ r)x}(:，t)满足式中，x1 (r, t)跟踪v(t),x2(r , t)收敛于“广义函数”v (t)的“广义导数”。
系统式(3)称做系统式(2)派生的“跟踪微分器”。
系统式(1)称做“快速跟踪微分器”。
3)“快速跟踪微分器”的离散形式用跟踪微分器式(1)来进行数值计算，进入稳态’，时易产生“高频颤振”，把sgn ( x)改成sat ( x, d)也不能使之避免。
为此，我们给出“跟踪微分器”的离散形式。
设离散系统为:直接对上式求“快速控制最优综合函数”，得式中，h为积分步长。
有离散系统为：系统式((4)是很好的数值微分器，称做“快速离散跟踪微分器。
把函数fst(。
)中的变量h取成与步长h相互独立的新变量ho，得系统式(5)有两个可调参数:，r, ho:决定跟踪速度，称做“速度因了”;h。
起对噪声的滤波作用，称做“滤波因了”。
注1:函数fst (,,:，ho)在控制和信号理中的作用非常广泛。
4安排过渡过程在一般的控制系统中，误差直接取成:e=v-y式中，v为设定值,y为系统输出。
误差的这种取法使初始误差很大，易引起“超调”，很不合理。
根据对象承受的能力，我们先安排合理的过渡过程，然后误差取成e=-y.这是解决PID的“快速性’，和“超调，，之问矛盾的有效办法，也是提高调节器“鲁棒性”的一种办法。
跟踪微分器的阶跃响应为:对系统输入V0=1的阶跃信号。
vl(t)表示安排的过渡过程，无超调;v2(t>表示其微分信号。
阶跃响应曲线如图2所示。
图2阶跃响应曲线图安排过渡过程的原则选加速度形状，先正，后负，正部分面积与负部分面积相等;积分两次，得单调上升、无条件超调的过渡过程，如图3所示。
图3安排过渡过程曲线图5非光滑(非线性)反馈效应考察一阶误差系统e=w+u对上式实施误差的线性反馈u=,k>0如果存在一常数> 0,满足<,则当>/k时，有<0，即“稳态误差，，或“静差，，小于/k。
即在线性反馈之下，稳态误差与反馈增益k成反比。
“非光滑(非线性)反馈”当>/k时，有<0，因此系统的“静差”最终要小于(/k)'/a。
取=1,k=10,a 2;0.5;0.25,则稳态误差(/k )1/“分别是减小，就以数量级的方式减小稳态误差。
若取=0,则反馈形式u=--k()为变结构控制。
线性反馈:增益反比的方式抑制扰动;非光滑反馈:数量级的方式抑制扰动。
当α=0时,反馈为变结构形式,完全抑制了扰动。
变结构控制对模型和扰动独立的机理就在于此。
取=1,k=1.5,α:2;1;1/2;1/3;1/5,则静差图如图4所示。
图4不同反馈的系统静差图不同反馈的系统静差图误差衰减的动态特性:设误差方程为:上式的通解为：式中，t/k(1-)当> 1时(t)以的速度衰减;当=1时，e (t)以exp (-kt)的速度“指数衰减”;当a<1时，在/k(1-a)时刻，=0:，即“有限时间衰减”这里时是“光滑反馈”<1时是“非光滑反馈”=0时是“变结构控制”。
注2;“非光滑反馈”的效率比“光滑反馈”好。
“光滑反馈”里，“指数衰减率”最好;“非光滑”反馈里，“指数衰减率”最不好。
6非线性PID利用跟踪微分器(TD>，把经典PID改造成“非线性PID;，其结构如图5所示。
图5非线性PID结构图这里TD给出跟踪输出Y的量及其微分z2;误差、积分、微分是由安排的过渡过程和TD的输出z2来产生的把原先的“加权和”改成“非线性组合”而得“非线性PID"。
一种可用的“非线性组合”形式为:当a> 1时，fal函数具有:小误差，大增益;大误差，小增益的特性。
“非线性PID'，的控制律为式中，，甚至可取<0,0<2,>1也可采用其他合适的“非线性组合”。
7扩张状态观测器(ESO对于系统方程-系统:称为经典状态观测器。
这两个系统的误差方程为:矩阵A一LC稳定时，z (t)渐近地估计状态变量x(t>。
如果L是依噪声特性按最小方差律确定的，则这个状态观测器就是卡尔曼滤波器。
考虑系统若厂(x1, x2, t)为已知，则其观测器可设计为:问题:很多情况下f (,, t)未知，因此不能应用f (,, t )，那么如何构造状态观测器呢?当f (,, t)未知时，把f (,, t)当作扰动，用“非光滑反馈”效应抑制其作用。
令=f (,, t)，=g(,t)，则g(,, t)也是未知函数，于是有式中a}，可取a}--0. 5=1/2, a2=0.25=1/40被扩张的状态对“未知扰动”的“实时作用量”a (t)=f(t)作出很好的估计。
系统式(7)叫做系统式(6)的“扩张状态观测器”若(, t)，已知，取则有式中，系统的“。
)是系统的“内扰”和“外扰”的总和，即总扰动”。
ESO的:估计的是“总扰动”中未知部分的“实时作用量”当控制量时，对象近似地变成为:系统被“线性化”成“积分器串联型”。
这是不确定系统的“实时动态线性化，。
“系统设计”问题变成对“积分器串联型系统的设计”问题。
8自抗扰控制器(Active Disturbances Re- jection Controller, ADRC)利用TD和ESO，给出如下ADRC控制器方案，如图6所示。
当对象有已知部分f。
(。
)时，ADRC结构如图7所示。
这里不再需要“误差积分”反馈。
“自抗扰”意义在于”补偿”项一系统的“未建模动态”和“未知外扰”作用一并给予估计和补偿[”]。
“自抗扰控制器”算法:被控对象:x= f (x, z, w, t )}bu, y一x1)安排过渡过程v。
为设定值。
或其他合适办法。
1) 估计状态和总扰动((ESO方程)2)3) 3)控制量的形成式中这个控制器的算法只需对象的输入输出数据u (k)和y (k)。
被控对象的函数有已知部分，控制器算法中的u (k)和ESO改为9“控制问题”的描述从自抗扰控制器的作用机理看，我们从另外一个角度描述控制问题。
从控制的目的来看，对于下面两个系统它们的控制问题没有什么区别。
①被控对象以一定范围变化的f (t)和输入量u所驱动的动态系统为:记,F为动态系统的集合。
②控制目标输入,所激励的一动态过程( t >的输出所成的集合V③控制器以:为输入、输出、控制量，且含有可调参数p的动态系统，用C (p)表示。
①控制问题用表示如下“控制问题”:设计一控制器C(p)，对控制器C (p)所产生的控制量u(t)都能使输出y (t)跟踪目标v (t)10结语本文从传统的PID原理及其结构进行分析，揭示了传统PID的优缺点，并本着继承其优点，克服其缺点的原则，逐步阐述了自抗扰控制技术的基本思想。
这项新的控制技术的核心是把系统的未建模动态和未知外扰作用都归结为对系统的“总扰动”而进行估计并给予补偿。
采用的方法是充分运用特殊的“非线性”效应。
这种方法具有如下诸多优点:安排过渡过程解决了“快速性和超调之间的矛盾”;不用1反馈也能实现“无静差”，避免了积分反馈的副作用;统一处理确定系统和不确定系统的控制问题;不存在“鲁棒性”问题，只有控制器的“鲁棒性”、“适应范围”;抑制外扰，不一定要知道其模型或要直接测量;同一个ADRC!控制“时间尺度”相当的一对象;线性、非线性对象一视同仁，不用区分;实现控制，不一定要进行“辨识”;解藕控制，只需考虑静态藕合”，不用考虑“动态藕合”;ADRC容易控制时滞系统等。
