导数的计算及其几何意义

导数的几何意义有什么导数的几何意义有什么呢?同学们还有印象吗。

如果没有了，快来小编这里瞧瞧。

下面是由小编为大家整理的“导数的几何意义有什么”，仅供参考，欢迎大家阅读。

导数的几何意义有什么导数(Derivative)是微积分中的重要基础概念。

当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。

在一个函数存在导数时，称这个函数可导或者可微分。

可导的函数一定连续。

不连续的函数一定不可导。

导数实质上就是一个求极限的过程，导数的四则运算法则来源于极限的四则运算法则。

函数y=fx在x0点的导数f'x0的几何意义表示函数曲线在P0[x导数的几何意义0fx0] 点的切线斜率。

导数的几何意义是该函数曲线在这一点上的切线斜率。

导数的应用导数与物理几何代数关系密切.在几何中可求切线在代数中可求瞬时变化率在物理中可求速度加速度.导数亦名纪数、微商微分中的概念是由速度变化问题和曲线的切线问题矢量速度的方向而抽象出来的数学概念.又称变化率.如一辆汽车在10小时内走了600千米它的平均速度是60千米/小时.但在实际行驶过程中是有快慢变化的不都是60千米/小时.为了较好地反映汽车在行驶过程中的快慢变化情况可以缩短时间间隔设汽车所在位置s与时间t的关系为s=ft那么汽车在由时刻t0变到t1这段时间内的平均速度是[f(t1)-f(t0)]/[t1-t0]当 t1与t0无限趋近于零时汽车行驶的快慢变化就不会很大瞬时速度就近似等于平均速度。

自然就把当t1→t0时的极限lim[f(t1)-f(t0)]/[t1-t0] 作为汽车在时刻t0的瞬时速度这就是通常所说的速度.这实际上是由平均速度类比到瞬时速度的过程如我们驾驶时的限“速” 指瞬时速度。

拓展阅读：导数的概念及其几何意义的数学知识点一般地，对于函数y =f(x)，x1,x2是其定义域内不同的两点，那么函数的变化率可用式表示，我们把这个式子称为函数f(x)从x1到x2的平均变化率，习惯上用表示，即平均变化率上式中的值可正可负，但不为0.f(x)为常数函数时，瞬时速度:如果物体的运动规律是s=s(t)，那么物体在时刻t的瞬时速度v就是物体在t到这段时间内，当时平均速度的极限，即若物体的运动方程为s=f(t),那么物体在任意时刻t的瞬时速度v(t)就是平均速度v(t，d)为当d趋于0时的极限.函数y=f(x)在x=x0处的导数的定义:一般地，函数y=f(x)在x=x0处的瞬时变化率是，我们称它为函数y=f(x)在x=x0处的导数，记作或，即。

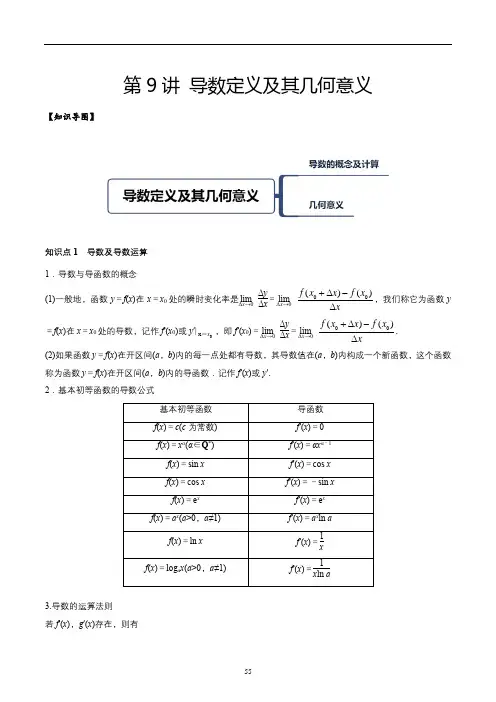
第9讲 导数定义及其几何意义【知识导图】知识点1 导数及导数运算 1．导数与导函数的概念(1)一般地，函数y ＝f (x )在x ＝x 0处的瞬时变化率是lim Δx →0Δy Δx ＝lim Δx →000()()f x x f x x+∆−∆，我们称它为函数y ＝f (x )在x ＝x 0处的导数，记作f ′(x 0)或y ′|0x x ＝，即f ′(x 0)＝lim Δx →0Δy Δx ＝lim Δx →000()()f x x f x x+∆−∆. (2)如果函数y ＝f (x )在开区间(a ，b )内的每一点处都有导数，其导数值在(a ，b )内构成一个新函数，这个函数称为函数y ＝f (x )在开区间(a ，b )内的导函数．记作f ′(x )或y ′. 2．基本初等函数的导数公式3.导数的运算法则 若f ′(x )，g ′(x )存在，则有(1)[f (x )±g (x )]′＝f ′(x )±g ′(x )； (2)[f (x )·g (x )]′＝f ′(x )g (x )＋f (x )g ′(x )；(3)⎣⎡⎦⎤f (x )g (x )′＝f ′(x )g (x )－f (x )g ′(x )[g (x )]2(g (x )≠0)．例题1.1 求下列函数的导数：(1)y ＝ln x ＋1x ；(2)f (x )＝sin x2⎝⎛⎭⎫1－2cos 2x 4；(3)y ＝3x e x －2x ＋e. 答案 (1) y ′＝1x －1x 2，(2) f ′(x )＝－12cos x ，(3) y ′＝(ln 3＋1)·(3e)x －2x ln 2解析 (1)y ′＝⎝⎛⎭⎫ln x ＋1x ′＝(ln x )′＋⎝⎛⎭⎫1x ′＝1x －1x2. (2)因为f (x )＝sin x 2⎝⎛⎭⎫－cos x 2＝－12sin x ， 所以f ′(x )＝⎝⎛⎭⎫－12sin x ′＝－12(sin x )′＝－12cos x . (3)y ′＝(3x e x )′－(2x )′＋e′＝(3x )′e x ＋3x (e x )′－(2x )′＝3x e x ln 3＋3x e x －2x ln 2＝(ln 3＋1)·(3e)x －2x ln 2.例题1.2设函数f (x )＝e x x ＋a .若f ′(1)＝e4，则a ＝________.答案 1解析 由f ′(x )＝e x （x ＋a ）－e x （x ＋a ）2，可得f ′(1)＝e a （1＋a ）2＝e 4，即a （1＋a ）2＝14，解得a ＝1.例题1.3 已知函数f (x )的导函数为f ′(x )，且满足关系式f (x )＝x 2＋3xf ′(2)＋ln x ，则f (1)＝________. 答案 －234解析 因为f (x )＝x 2＋3xf ′(2)＋ln x ，∴f ′(x )＝2x ＋3f ′(2)＋1x.令x ＝2，得f ′(2)＝4＋3f ′(2)＋12，则f ′(2)＝－94.∴f (1)＝1＋3×1×⎝⎛⎭⎫－94＋0＝－234.知识点2 导数的几何意义函数y ＝f (x )在点x 0处的导数的几何意义，就是曲线y ＝f (x )在点P (x 0，f (x 0))处的切线的斜率k ，即k ＝f ′(x 0)．例题2.1 (1)曲线y ＝3(x 2＋x )e x 在点(0，0)处的切线方程为________.(2)曲线y ＝ln x ＋x ＋1的一条切线的斜率为2，则该切线的方程为________.答案 (1) 3x －y ＝0，(2) 2x －y ＝0解析 (1)y ′＝3(2x ＋1)e x ＋3(x 2＋x )e x ＝3e x (x 2＋3x ＋1)，所以曲线在点(0，0)处的切线的斜率k ＝e 0×3＝3，所以所求切线方程为3x －y ＝0.(2)设切点坐标为(x 0，y 0)，因为y ＝ln x ＋x ＋1，所以y ′＝1x＋1，所以切线的斜率为1x 0＋1＝2，解得x 0＝1.所以y 0＝ln 1＋1＋1＝2，即切点坐标为(1，2)，所以切线方程为y －2＝2(x －1)，即2x －y ＝0.例题2.2 在平面直角坐标系xOy 中，点A 在曲线y ＝ln x 上，且该曲线在点A 处的切线经过点(－e ，－1)(e 为自然对数的底数)，则点A 的坐标是_______，此时切线方程为_______.答案 (e ，1)， x －e y ＝0解析 设A (m ，n )，则曲线y ＝ln x 在点A 处的切线方程为y －n ＝1m(x －m ).又切线过点(－e ，－1)，所以有n ＋1＝1m(m ＋e).再由n ＝ln m ，解得m ＝e ，n ＝1.故点A 的坐标为(e ，1)，切线方程为x －e y ＝0.例题2.3 已知y ＝f (x )是可导函数，如图，直线y ＝kx ＋2是曲线y ＝f (x )在x ＝3处的切线，令g (x )＝xf (x )，g ′(x )是g (x )的导函数，则g ′(3)＝________.答案 0解析 由题图可知曲线y ＝f (x )在x ＝3处切线的斜率等于－13，∴f ′(3)＝－13.∵g (x )＝xf (x )，∴g ′(x )＝f (x )＋xf ′(x )，∴g ′(3)＝f (3)＋3f ′(3)，又由题意可知f (3)＝1， ∴g ′(3)＝1＋3×⎝⎛⎭⎫－13＝0. 例题2.4 已知函数f (x )＝a e x (a >0)与g (x )＝2x 2－m (m >0)的图象在第一象限有公共点，且在该点处的切线相同，当实数m 变化时，实数a 的取值范围为( ) A.⎝⎛⎭⎫4e 2，＋∞B.⎝⎛⎭⎫8e 2，＋∞C.⎝⎛⎭⎫0，4e 2D.⎝⎛⎭⎫0，8e 2 答案 D解析 设在第一象限的切点为A (x 0，y 0)，所以⎩⎨⎧a e x 0＝2x 20－m ，a e x 0＝4x 0，整理得⎩⎨⎧4x 0＝2x 20－m ，x 0>0，m >0，由m ＝2x 20－4x 0>0和x 0>0，解得x 0>2.由上可知a ＝4x 0e x 0，令h (x )＝4xe x ，x >2，则h ′(x )＝4（1－x ）e x.因为x >2，所以h ′(x )＝4（1－x ）e x<0，h (x )＝4xe x 在(2，＋∞)上单调递减， 所以0<h (x )<8e2，即a ∈⎝⎛⎭⎫0，8e 2.。

导数的概念，计算，几何意义（一）知识点 1.平均变化率：函数()f x 从1x 到2x 的平均变化率为 ，若21x x x ∆=-21y y y ∆=-则，平均变化率可表示为 。

2．导数的概念：函数()y f x =的导数'()f x ，就是当0x ∆→时，函数的增量y ∆与自变量的增量x ∆的比yx∆∆（平均变化率） 的 ， 即'()f x ＝ ＝ ． 3．导函数：函数()y f x =在区间(,)a b 内 的导数都存在，就说()f x 在区间(,)a b 内 .其导数也是(,)a b 内的函数，叫做()f x 的 ，记作'()f x 或'x y ， 函数()f x 的导函数'()f x 在0x x =时的导函数值 ，就是)(x f 在0x 处的导数.4．导数的几何意义：设函数()y f x =在点0x 处可导，那么它在该点的导数等于函数所表示曲线在相应点),(00y x M 处的 。

相应的切线方程为 （点斜式） 。

5．求导数的方法： (1) 八个基本求导公式()c 为常数'c ＝ ； ()'n x ＝ ； (sin )'x ＝ ， (cos )'x ＝ ()'x a ＝ ， ()'x e ＝(log )'a x ＝ ， (ln )'x ＝(2) 导数的四则运算(()())f x g x '±＝ [()]Cf x '＝ (()())f x g x '＝ ， ()()()f xg x '＝ 推论：()c 为常数[()]'cf x = ；21'()[]'()()f x f x f x =-； ()''''fgh f gh fgh fgh =++(3) 复合函数的导数设()u x θ=在点x 处可导，()y f u =在点()u x θ=处可导，则复合函数[()]f x θ在点x 处可导， 且'()f x ＝ ，即'''x u x y y u =. 典型例题：例1．（变化率）求函数y=12+x 在x 0到x 0+Δx 之间的平均变化率.解 ∵Δy=11)(11)(11)(2202020220+++∆+--+∆+=+-+∆+x x x x x x x x x.11)(2,11)()(220200202020+++∆+∆+=∆∆∴+++∆+∆+∆=x x x xx x y x x x x x x变式训练1.1.设函数()f x 在0x 处可导，则000()()limx f x x f x x∆→-∆-=∆（ ）A ．0'()f x B.0'()f x - C.0()f x D.0()f x -2.若函数()y f x =在区间(,)a b 内可导，且0(,)x a b ∈，则000()()limh f x h f x h h→+--=A.0'()f xB. 02'()f xC. 02'()f x -D.0例2. 求下列各函数的导数： （1）;sin 5x xx x y ++=（2）);3)(2)(1(+++=x x x y（3）;4cos 212sin 2⎪⎭⎫⎝⎛--=x x y （4）.1111xxy ++-=解 (1)∵,sin sin 23232521x x x xx x x x y ++=++=-∴y′.cos sin 2323)sin()()(232252323x x x x x x x x x x-----+-+-='+'+'=（2）y=（x 2+3x+2）（x+3）=x 3+6x 2+11x+6，∴y′=3x 2+12x+11.（3）∵y=,sin 212cos 2sin x x x =⎪⎭⎫ ⎝⎛--∴.cos 21)(sin 21sin 21x x x y ='='⎪⎭⎫ ⎝⎛='（4）xx x xx x x y -=+--++=++-=12)1)(1(111111， ∴.)1(2)1()1(21222x x x x y -=-'--='⎪⎭⎫ ⎝⎛-=' 变式训练2：（1）求y=tanx 的导数.解 y′.cos 1cos sin cos cos )(cos sin cos )(sin cos sin 22222x x xx x x x x x x x =+='-'='⎪⎭⎫ ⎝⎛=（2）求下列各函数的导数：①2(1)(231)y x x x =++- ②y ③()(cos sin )x f x e x x =⋅+利用导数求切线方程 例3：如果曲线103-+=x x y 的某一切线与直线34+=x y 平行，求切点坐标与切线方程． 分析：本题重在理解导数的几何意义：曲线()y f x =在给定点00(,())P x f x 处的切线的斜率0()k f x '=，用导数的几何意义求曲线的斜率就很简单了。

导数的几何意义解析与归纳导数是微积分中的重要概念，它描述了函数在某一点的变化率。

导数不仅在数学领域有着广泛的应用，而且在几何学中也有着重要的几何意义。

本文将对导数的几何意义进行解析与归纳，以帮助读者更好地理解这一概念。

1. 导数的定义与几何意义首先，我们来回顾一下导数的定义。

对于函数f(x)，在点x处的导数可以通过以下极限来定义：f'(x) = lim(h->0) [f(x+h)-f(x)]/h直观上，这个定义可以理解为函数f(x)在点x处的切线的斜率。

这意味着导数可以描述函数在某一点的变化趋势。

2. 导数与函数的递增与递减性根据导数的定义，我们可以得出以下结论：如果函数f(x)在某个区间内的导数大于零，那么函数在该区间内是递增的；如果导数小于零，那么函数是递减的。

这是因为导数描述了函数的变化率，正值表示函数在该点上升，负值表示函数在该点下降。

3. 导数与函数的极值点导数还可以帮助我们找到函数的极值点。

如果函数f(x)在某一点x处的导数为零，那么这个点可能是一个极值点。

具体而言，如果导数由正变负，那么这个点是极大值点；如果导数由负变正，那么这个点是极小值点。

这是因为导数为零表示函数的变化率为零，也就是函数在该点存在水平切线，可能对应着极值点。

4. 导数与函数的拐点除了极值点，导数还能帮助我们找到函数的拐点。

拐点是函数曲线由凸变凹或由凹变凸的点。

我们可以通过导数的变化来判断函数的拐点。

如果函数f(x)在某一点x处的导数由正变负或由负变正，那么这个点可能是一个拐点。

5. 导数与函数的图像在坐标平面上，函数的导数可以帮助我们画出函数的图像。

我们可以通过导数的正负性来确定函数曲线的大致形状。

例如，如果导数在某一区间内始终为正，则函数在该区间上是递增的，曲线会向上凸起；如果导数在某一区间内始终为负，则函数在该区间上是递减的，曲线会向下凸起。

同样地，我们还可以根据导数为零或无定义的点来确定函数图像的特殊点，如极值点、拐点等。

第01讲：导数的概念、几何意义 导数的计算高考《考试大纲》对文科考生的要求：① 了解导数概念的实际背景； ② 理解导数的几何意义； ③ 能根据导数定义，求函数xy x y x y C y 1,,,2====的导数 ④ 能利用下面给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数， 常见基本初等函数的导数公式和常用导数运算公式 ：+-∈==N n nx x C C n n ,)(;)(01''为常数； ;sin )(cos ;cos )(sin ''x x x x -==a a a e e x x x x ln )(;)(''==； ax x xx a ln 1)(log ;1)(ln ''==法则1： )()()]()(['''x v x u x v x u ±=± 法则2： )()()()()]()(['''x v x u x v x u x v x u +=法则3： )0)(()()()()()(])()([2'''≠-=x v x v x v x u x v x u x v x u（一）基础知识回顾：1. 平均变化率：式子1212)()(x x x f x f --叫做函数)(x f y =从1x 到2x 的平均变化率，表示为x ∆∆f ;设))(,(,)(,222111x f x P x f x P ）（，则平均变化率x∆∆f的几何意义是____________________. 2.导数的定义：函数)(x f y =在0x 处的瞬时变化率xx f x x f x yo x x ∆-∆+=∆∆→∆→∆)()(limlim 000称为函数)(x f y =在0x x =处的导数，记作)(0/x f 或0/x x y =，即xx f x x f x f x ∆-∆+=→∆)()(lim)(0000/3.导数的几何意义：函数)(x f y =在0x 处的导数是曲线)(x f y =上点()(,00x f x )处的切线的斜率。

导数的概念及其几何意义
导数是微积分中一个重要的概念，它描述了函数在某一点的变化率。

导数的几何意义是指函数在一点的导数等于函数图形上对应点的切线斜率。

当函数在某一点取某个值时，函数在该点的切线方向和该点处的法线方向相同，而切线斜率就是法线斜率。

因此，导数的几何意义可以看作是函数在某一点处切线的斜率。

导数的概念来源于微积分中的极值问题。

我们可以使用导数来寻找函数的极值点，特别是寻找函数的零点和极值点。

在求解微积分问题时，导数也是一个常用的工具。

例如，在求解函数的最大值和最小值时，我们可以使用导数来找到函数的极值点，进而求解最大值和最小值。

此外，导数还可以用于求解曲线的最值问题，例如求曲线的最小值或最大值。

总结起来，导数是微积分中一个非常重要的概念，它描述了函数在某一点的变化率，具有广泛的应用。

在求解微积分问题时，我们应该熟练掌握导数的概念和应用，以便更好地解决问题。

导数的几何意义和物理意义导数是微积分学中的重要概念，它具有丰富的几何意义和物理意义。

本文将分别从几何和物理两个角度，详细探讨导数的几何意义和物理意义。

一、导数的几何意义导数在几何中有着重要的意义。

在几何上，导数表示了函数曲线在某一点上的切线斜率。

具体来说，对于函数f(x)，如果在点x=a处存在导数，那么导数f'(a)就是函数曲线在该点上的切线的斜率。

切线斜率的意义在于它反映了函数曲线的变化速率。

当函数的导数为正时，表示函数在该点上递增；当函数的导数为负时，表示函数在该点上递减；而导数等于零时，表示函数在该点上取得极值。

利用导数，我们可以精确地描述函数曲线的变化趋势。

此外，导数还可以用来计算函数曲线在某一点的局部变化率。

例如，当我们求解速度函数的导数时，得到的导数表示了物体在该时刻的瞬时加速度。

这就引出了导数在物理意义方面的应用。

二、导数的物理意义导数在物理学中有着广泛的应用，其中最为常见的是它对位移、速度和加速度的描述。

1. 位移：对于一维运动而言，物体在某一时刻的位移可以表示为位移函数的导数。

例如，当我们求解位移函数的导数时，得到的导数就表示了物体在该时刻的瞬时速度。

2. 速度：速度是指物体在单位时间内所改变的位移，它是位移关于时间的导数。

具体而言，速度函数的导数表示了物体在某一时刻的瞬时加速度。

3. 加速度：加速度是指物体在单位时间内所改变的速度，它是速度关于时间的导数。

当我们求解速度函数的导数时，得到的导数表示了物体在该时刻的瞬时加速度。

通过上述例子可以看出，导数在物理学中的应用十分广泛。

它不仅可以描述物体的运动状态，还可以帮助我们分析运动规律，解决各种与运动相关的问题。

结论综上所述，导数具有重要的几何意义和物理意义。

从几何上看，导数表示了函数曲线在某一点上的切线斜率，反映了函数曲线的变化速率；从物理上看，导数用于描述位移、速度和加速度等与运动相关的概念。

通过对导数的研究和应用，我们可以深入理解函数的特性和物体的运动规律，为实际问题的解决提供了有力的工具和方法。

导数的概念、几何意义及其运算导数的概念、几何意义及其运算常见基本初等函数的导数公式和常用导数运算公式：«Skip Record If...»；«Skip Record If...»«Skip Record If...»；«Skip Record If...»法则1：«Skip Record If...»法则2：«Skip Record If...»法则3：«Skip Record If...»（一）基础知识回顾：1.导数的定义：函数«Skip Record If...»在«Skip Record If...»处的瞬时变化率«Skip Record If...»称为函数«Skip Record If...»在«Skip Record If...»处的导数，记作«Skip Record If...»或«Skip Record If...»，即«Skip Record If...»如果函数«Skip Record If...»在开区间«Skip Record If...»内的每点处都有导数，此时对于每一个«Skip Record If...»，都对应着一个确定的导数«Skip Record If...»，从而构成了一个新的函数«Skip Record If...»。

称这个函数«Skip Record If...»为函数«Skip Record If...»在开区间内的导函数，简称导数，也可记作«Skip Record If...»，即«Skip Record If...»＝«Skip Record If...»＝«Skip Record If...»导数与导函数都称为导数，这要加以区分：求一个函数的导数，就是求导函数；求函数«Skip Record If...»在«Skip Record If...»处的导数«Skip Record If...»，就是导函数«Skip Record If...»在«Skip Record If...»处的函数值，即«Skip Record If...»＝«Skip Record If...»。