当前位置：文档之家 › 角动量定理

角动量定理

  • 格式：pptx
  • 大小：1.09 MB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

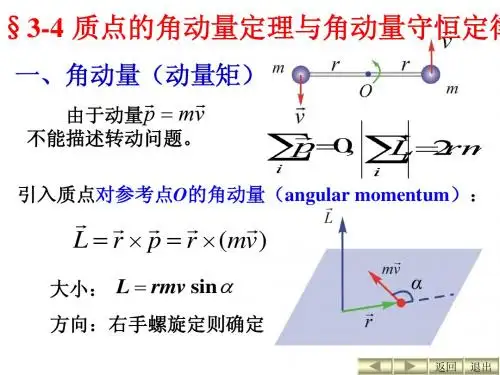
角动量定理 角动量守恒定律

角动量定理 角动量守恒定律

，质点对圆心的 特例：做圆周运动时，由于 r v 角动量大小为 L rmv ，
大小不变，方向不变。 质点对圆心O的角动角动量守恒定律
dL d dr d p Lrp (r p) pr dt dt dt dt dr dr v, p v (mv ) 0 dt dt
返回
退出
实验：质量为m的小球系在 轻绳的一端，绳穿过一竖 直的管子，一手握管，另 一手执绳。
实验发现： 则
v2r2 v1r1
mv2r2 mv r1 1
表明小球对圆心的角动量保持不变。 解释：作用在小球上的有心力对力心的力矩为零， 故小球的角动量守恒。
返回
退出
行星绕太阳的运动： 作用在行星上的万有引力（有心力）对太阳（力 心）的力矩为零，因此，行星在运动过程中，对太阳 的角动量保持不变。
§3-4 质点的角动量定理与角动量守恒定律
一、角动量（动量矩）
由于动量 不能描述转动问题。 引入质点对参考点O的角动量（angular momentum）：
L r p r (mv )
大小： L rmv sin 方向：右手螺旋定则确定
返回
退出
L r p r (mv )
r p 常矢量
pd 常量
在有心力场中，关于力心的角动量守恒。
返回
退出
例2-17 发射宇宙飞船去考察一质量m1半径 R 的行星， 当飞船静止于距行星中心 4R 处时，以速度 发射一 质量为 m2 (m2远小于飞船质量)的仪器, 要使仪器恰好 掠着行星的表面着陆，q角应是多少? 着陆滑行初速度 v 多大?
解：有心力场中， 运用角动量守恒和(m1 , m2 )系统 机械能守恒定律：
刚体定轴转动的角动量定理和角动量守恒定律

刚体定轴转动的角动量定理和角动量守恒定律

刚体定轴转动的角动量定理和角动量守恒定律
1、刚体定轴转动的角动量
刚体绕定轴转动的角动量等于刚体对该轴的转动惯量与角速度的乘积；方向与角速度的方向相同。

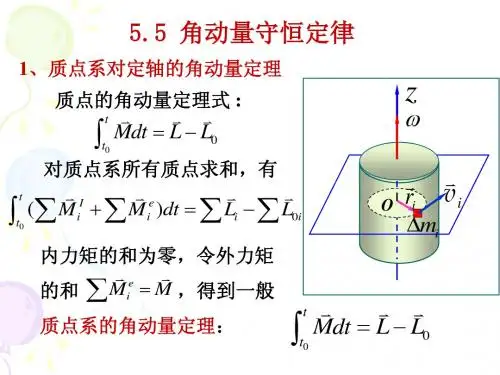
2、刚体定轴转动的角动量定理
（1）微分形式：刚体绕某定轴转动时，作用于刚体的合外力矩，等于刚体绕该定轴的角动量随时间的变化率。

（2）积分形式：当物体绕某定轴转动时，作用在物体上的冲量矩等于角动量的增量。

3、刚体定轴转动的角动量守恒定律
如果物体所受的合外力矩等于零，或者不受外力矩作用，物体的角动量保持不变。

练习：1角动量守恒的条件是 。

0=M 11222
1ωωJ J Mdt t t -=⎰刚体 ） 21J J ==ωJ 恒量
ωJ L =()ωJ dt d dt dL M ==。

角动量 角动量守恒定律

角动量 角动量守恒定律


角动量与线动量关系
角动量与线动量的关系
角动量是线动量在物体绕某点或某轴 转动时的表现形式，二者之间存在密 切关系。
动量守恒定律
在不受外力作用的情况下，物体的总 动量（包括线动量和角动量）保持不 变，即动量守恒定律。
02
角动量守恒定律
守恒条件及适用范围
守恒条件
当系统不受外力矩作用时，系统的角动量守恒。即在没有外力矩的情况下，系统内部各部分之间的相 互作用力不会导致系统总角动量的改变。
06
总结与展望
课程内容回顾与总结
角动量的定义与性
质
角动量是物体绕某点或某轴转动 的动量，具有矢量性质，其大小 与物体的质量、速度和转动半径 有关。
角动量守恒定律的
表述
在没有外力矩作用的情况下，系 统内的角动量保持不变，即角动 量守恒。
角动量守恒定律的
应用
角动量守恒定律在天体物理、刚 体转动、分子运动等领域有广泛 应用，如行星运动、陀螺仪工作 原理等。
对未来研究方向的展望
角动量守恒定律在复 杂系统较成熟，但在复 杂系统中的应用还有待深入研究， 如多体问题、非线性问题等。
角动量与其他物理量 的关系研究
角动量与能量、动量等物理量之 间存在一定的联系，未来可以进 一步探讨它们之间的关系，以及 如何利用这些关系解决实际问题。
在机械工程中，飞轮储能系统被应用 于能量回收和节能领域。飞轮储能系 统利用刚体定轴转动的角动量守恒定 律，通过加速和减速飞轮来储存和释 放能量。这种储能方式具有高效率、 环保等优点，在电动汽车、风力发电 等领域具有广阔的应用前景。
04
质点和质点系相对于固定 点角动量守恒
质点相对于固定点角动量定义和性质
双星系统由两颗互相绕转的恒星组成。在双星系统中，两颗恒星的角动量守恒，因此它们的轨道周期、距离和质量之 间存在一定关系。
角动量与角动量定理

角动量与角动量定理

rr pr
1
L
dt 2 dt 2 dt 2
2m
2m
太阳对行星的引力总是指向太阳，因而行星对太阳
中心的角动量守恒，L为常量，所以得证。
L rmv mr2
方向 垂直于圆面
② 质点作匀速直线运动时，角 动量守恒。
L rmv sin mvd
方向始终垂直纸面向外
r L
r pr r
O
Or
r
d
pr
③ 角动量与参考点的位置有关。
r L
因而在说明一个质点的角动量
pr
时，必须指明是相对于哪一个 参考点而言的。
O
rr
θ m
锥摆 O
l
m
O
v
且在高速低速范围均适用。
例题1：
证明行星运动的开普勒第二定律：行星对太阳
的矢径在相等的时间内扫过的面积相等。
r
L
解：行星位矢扫过的面积dS
dS
1
r
r dr
sin
1
rr drr
dS r
2
2
单位时间行星位矢扫过的面积
•
drr
dS 1 rr drr 1 rr drr 1 rr vr 1
vr
y
xp z
L z
xp y
yp x
L , L , L 分别称为角动量在x、y、z轴上的分 x yz
量式，或称为对x、y、z轴的角动量。
二、力矩
1、定义
力
r F
对参考点O

rr
r F
r
M
r
rr
F
θ
Or
m
大小：
M
rF
sin
角动量定理.pdf

角动量定理.pdf


A M r o
x2
m
解：在地面参考系中， 在地面参考系中，建立如图 x 坐 标，设滑轮半径为 r 有： B
l = AA′ + AB + BB′ = x1 + x2 + πr
B′
s
s = x1 − x 2
mAA′ m = ⋅ x1 , l
mAB
m = ⋅ πr l
m = ⋅ x2 , l
A′
x1
x
mBB′
µ
m2
ro m
m1
m2 和滑轮为研究对 解：在地面参考系中， 在地面参考系中，选取 m1 、 象，分别运用牛顿定律 分别运用牛顿定律和 牛顿定律和刚体定轴转动定律得 刚体定轴转动定律得：
T1
N
aT2T2o向里+Ny
m1
a
m1 g
µm2 g
m2
m2 g
Nx
T1
列方程如下： 列方程如下：
m 1 g − T1 = m 1 a T2 − µ m 2 g = m 2 a 1 2 T1 r − T 2 r = m r β 2 a = rβ
用隔离法列方程: (以逆时针方向为正) A M r o
CA x2 x1
m
T1
T2 CB . m Bg T1
B
CB
. CA
m Ag
Jr T2
B′
s
A′
m A g − T1 = m A a
x
T2 − mB g = mB a
T1r − T2 r = Jβ 2 2 J = J M + J AB = 1 Mr + m r AB 2
T1
r a1
以向下为正方向
5.5 角动量守恒定律

5.5 角动量守恒定律


例题1 ： 一粒子弹水平射入一静止悬杆的下端，穿出 后速度损失 3 / 4，求子弹穿出后棒的角速度 。已知轴处自由 。
解：以 f 代表杆对子弹的阻力，对子弹有: fdt m(v v0 ) 3mv0 / 4
子弹对杆的冲量矩为：

l f dt J f ldt
若 M 0 ，则
L J 常量
——刚体定轴转动的角动量守恒定律
讨论
内力矩不改变系统的角动量.
在冲击等问题中
M内 M外 L 常量
角动量守恒定律是自然界的一个基本定律. 刚体（或刚体组系统）角动量守恒的三种情况： ①J 不变（刚体），角速度ω的大小和方向均不变 ②J 可变（质点系），ω亦可变，但Jω乘积不变 ③刚体组的角动量守恒
a
v
m
3mva 2 2 m' l 3ma
射入竿后，以子弹、细杆和 地球为系统 ，机械能守恒 .
o
30
a
1 1 2 2 2 ( ml ma ) 2 3 l mga(1 cos 30) mg (1 cos 30) 2
2 2 v g (2 3 )( m l 2ma )( m l 3ma ) 6 ma
质点系的角动量定理：

t
t0
Mdt L L0
质点系的角动量定理：

t
t0
Mdt L L0
O

ri
mi
z
该矢量式向固定转轴（如 z轴） 的投影，得一个标量式，即
vi

t
t0
M z dt Lz L0 z
相对某固定轴，质点系所受的角冲量等于系统 角动量的增量。——质点系对定轴的角动量定理。
大学物理-角动量定理和角动量守恒定律

大学物理-角动量定理和角动量守恒定律

当系统所受外力矩为零时，系统内各物体角动量 之和保持不变。
系统内物体之间的相互作用力矩不会改变系统的 总角动量。
角动量守恒的应用举例
天体运动
行星绕太阳公转、卫星绕地球运 行等天体运动中，角动量守恒定
律是重要的理论基础。
陀螺仪
陀螺仪利用角动量守恒原理，通过 高速旋转来保持方向稳定，广泛应 用于导航、制导和控制系统。
机械系统
在机械系统中，如旋转机械、齿轮 传动等，角动量守恒定律用于分析 系统的动态平衡和稳定性。
04 角动量定理与守恒定律的 实际意义
在天文学中的应用
描述行星和卫星的运动
角动量定理和守恒定律在天文学中用于描述行星和卫星围绕中心天体的运动。 这些定律帮助科学家理解天体的旋转和轨道运动，以及它们之间的相互作用。
预测天文现象
通过应用角动量定理和守恒定律，科学家可以预测天文现象，如行星的轨道变 化、卫星的旋转等。这些预测有助于更好地理解宇宙的演化。
在航天工程中的应用
航天器姿态控制
角动量定理和守恒定律在航天工程中用于控制航天器的姿态 。通过合理地布置航天器上的动量轮，可以调整航天器的角 动量，实现姿态的稳定和控制。
L = m × v × r，其中L是 角动量，m是质量，v是 速度，r是转动半径。
角动量单位
在国际单位制中，角动量 的单位是千克·米²/秒 (kg·m²/s)。
角动量定理表述
角动量定理
01
对于一个封闭系统，其总角动量保持不变，即系统内力的力矩
之和为零。
表述形式
02
dL/dt = ΣM = 0，其中dL/dt表示角动量的时间变化率，ΣM表
角动量守恒的应用
角动量守恒定律在许多物理现 象中都有应用，如行星运动、 陀螺仪等。
角动量定理、角动量守恒定律

角动量定理、角动量守恒定律


在 M d L 中 ，若 M 0 dt
即：J J
1
2
M 0 的原因可能有：
则 L常量
（1） F 0 （不受外力）
（2）外力作用于转轴上
（3）外力作用线通过转轴
（4）外力作用线与转轴平行
以上几种情况对定轴转动均没有作用，则刚
体对此轴的角动量守恒。
角动量守恒定律也适用于定轴转动系统。
例1：一个人站在有光滑固定转轴的转动平台上，双臂伸 直水平地举起两哑铃，在该人把此二哑铃水平收缩 到胸前的过程中，人、哑铃与转动平台组成的系统 的：
（A）机械能守恒，角动量守恒 （B）机械能守恒，角动量不守恒 （C）机械能不守恒，角动量守恒 （D）机械能不守恒，角动量不守恒
选C
像其他所有行星一样，太阳是由大量的灰尘雾和早 先充满宇宙空间的气体所组成。在几十亿年的时间内， 这些物质在引力的吸引下，慢慢缩聚起来，刚开始的时 候，这些气体团旋转的很慢，后来随着它们体积的缩小， 旋转速度不断提高，这个道理就和滑冰运动员把自己的 双臂逐渐收拢起来的时候，她的旋转速度就会不断加快 的道理一样。缩聚和旋转速度的加快，使组成太阳的物 质变成一个碟子般的东西。
2、刚体的角动量定理 在定轴转动中
MJaJddJ
dt dt
积分形式：
0 tM d tL L 1 2d L L 2 L 1 J2 J1
左边为对某个固定转轴的外力矩的作用在某段时间内 的积累效果，称为冲量矩。 右边为刚体对同一转动轴的角动量的增量。
3、角动量守恒定律
盘状星系——角动量守恒的结果
例2：有一个半径为R的水平圆转台，可绕通过其中心的竖 直固定光滑轴转动，转动惯量为J，开始时转台以匀 角速度 0 转动，此时有一质量为m的人站在转台中 心。随后人沿半径向外跑去，当人到达转台边缘时 转台的角速度为：
角动量守恒定律

角动量守恒定律




0 L v0 ; L v 2 2
得：
v0 v 9
注意：区分两类冲击摆 质点 质点 柔绳无切向力 （1） o • 水平方向： Fx =0 ， px 守恒
v0
l
m (2)
Fy
M
L • 对 o 点：M 0 ，
m v 0l = ( m + M ) v l
m v 0= ( m + M ) v
守恒
Fx
质点
定轴刚体（不能简化为质点）
o
v0
m
l
轴作用力不能忽略，动量不守恒， 但对 o 轴合力矩为零，角动量守恒
M
mv 0 l ml 2 1 Ml 2 3
v l
回顾习题
P84 4 -10
F
O
m M
F轴 0 m M系统 p 不守恒; M轴 0 m M系统 对O点角动量守恒 m 2 gh R m M vR
角动量守恒定律： 当质点系所受外力对某参考点（或轴）的力矩的矢 量和为零时，质点系对该参考点（或轴）的角动量 守恒。
注意
1.与动量守恒定律对比
当 F外 0 时，
当 M外 0 时，
2.守恒条件 能否为
p 恒矢量 L 恒矢量
或
?
彼此独立
M外 0
M轴 0

M 外 dt 0
m 以速度v 0 撞击 m 2 ，发生完全非弹性碰撞
求：撞后m 2的速率 v ?
解1：m 和 m 2 系统动量守恒
m v 0 = (m + m 2 ) v
A
解2： m 和 (m1 + m 2 )系统动量守恒
-角动量定理角动量守恒定律

-角动量定理角动量守恒定律


太原理工大学物理系
结论： 1）内力对定点的力矩之和为零。 2）只有外力矩才能改变系统的总角动量。 3.质点系的对轴的角动量
L Lxi Ly j Lzk M Mxi M y j Mzk
质点系对x轴的角动量定理
Mx

dLx dt
太原理工大学物理系
质点系的角动量守恒定律可以表示为三 个分量形式
解：小球的合外力矩为 0 ，故角动量守恒 。 有：
L = mvr = 恒量 即： m v1 r1 =m v2 r2
v2

r1v1 r2
太原理工大学物理系
五、质点系的角动量与角动量守恒
1.质点系对定点的角动量
P2
第i个质点对o点的角动量

r2
Li ri Pi
o
质点系对o点的角动量
ri fi 质点系受到的内力矩的矢量和
i
太原理工大学物理系
可以证明：内力 对定 点的力矩之和为零，即
ri fi 0
i
质点系内的重要结论之三

有 M
ri Fi
i
M外

dL dt
质点系的角动量定理：质点系对某定点的角动量的
时间变化率等于质点系对该点的合外力矩。
力矩在y轴方向的分量
M y zFx xFz
力矩在z轴方向的分量
M z xFy yFx
太原理工大学物理系
力矩在某一方向的分量称为力对该轴的力矩。
当质点在oxy平面内运动时，质点
z 所受的力也在该平面时，角动量和力
矩只有在z轴有分量。
Lx 0 Ly 0 Lz L
Mx 0 My 0 Mz M
角动量定理和角动量守恒定律

角动量定理和角动量守恒定律

角动量定理和角动量守恒定律
角动量定理和角动量守恒定律是描述刚体运动时的两个基本定律。

下面进行简单的介绍：
1. 角动量定理
角动量定理是描述角动量变化的定律。

它表示为：物体所受外力矩等于物体角动量对时间的变化率。

即
I*ω= ΔL/Δt
其中，I 为物体的转动惯量，ω为物体的角速度，L 为物体的角动量。

这个定理表明了一个物体的角动量发生变化时，必定受到了外部的力矩作用，即力矩等于角动量的变化率。

2. 角动量守恒定律
角动量守恒定律是描述角动量不变的定律，即如果没有外部力矩作用，系统的总角动量保持不变。

即：
L = L0
其中，L 为系统的总角动量，L0 为系统在某一时刻的总角动量。

这个定律表明，如果没有外部力矩作用，那么系统的总角动量保持不变。

如果一个物体在自由运动时，角动量发生变化，那么它将会改变自身的旋转状态（比如转速、方向等）。

总之，角动量定理和角动量守恒定律是描述刚体运动和角动量变化的基本定理，可以帮助我们更好地理解物体的运动和变化规律。

角动量定理


解：r1 = R + h1 = 6.64 × 10 km
3
h1
r2 = R + h2 = 8.20 × 10 3 km
角动量守恒：1 mv1 = r2 mv 2 r r1 v 2 = v1 = 6.58km ⋅ s −1 r2
作用于杆的力有重力及 轴对杆的支承力 N , N 过 O 点 , l 其力矩为零 .重力矩为 mg cos θ . 2 θ l l A = ∫ mg cos θ dθ = mg sin θ 0 2 2
由转动动能定理得 1 1 2 mgl sin θ = Iω − 0 2 2
还可以用机械能守恒
ω = ( mgl sin θ ) / I = ( 3 g sin θ ) l
1 2 dω dθ 1 2 dω = ml = ml ω 3 dθ dt 3 dθ θ g ω l 分离变量积分 ∫0 2 cosθ dθ = ∫0 3 ω dω 3g ω = (3 g sin θ ) l θ = 300 , ω = 2l 2 3 dt
θ = 900 , ω =
3g l
12
也可以用动能定理
0
θ
∫ ω
0
Idω
I IM θ = ωm = 2 K K
m
10
三、刚体定轴转动的功能关系
dω 将M = Iβ = I 两边同乘以 dθ 并积分 dt ω θ dω ∫θ Md θ = ∫ I dt d θ = ∫ω I ω d ω 1 2 1 2 刚体的动能定理 A = Iω − Iω 0 = Ek − Ek 0 2 2
10 1
∫ Mdt
t0
t
是合力矩对时间的积分，称为冲量矩。
2
（三）刚体对定轴的角动量

3.4 角动量定理 角动量守恒定律


r L
L = rpsinα = mrvsinα
r r 大小： 大小： L = r P sin α
r r 方向： 方向：垂直 r， P 组成的平面
S
α r
P
r r
O
特例： 特例：质点作圆周运动
L = rp = mrv
1
SI
2
kgm /s
2
r 量纲： 量纲： L = M L 2 T
第3章 动量与角动量
m
r0
v
R
OM
v0
θ
质点的动量矩守恒 1 GMm 1 2 GMm 2 mv0 = mv 2 r0 2 R
mv0r0sinθ = mvR
v0r0sinθ v= = 4v0sinθ R
3GM v =v0 1+ 2 v 2R 0
1/ 2
1 3GM sinθ = 1+ 2 4 2R 0 v
∑
i
r r ri × f i = 0
i
i
i
内力对定点的力矩之和为零
(自证 自证) 自证
r 质点系内的重要结论之三 r r dL r L = ∑ Li M外 = i dt
第3章 动量与角动量
13
冲量矩
r r r r r t2 L2 r ∫ M外dt = ∫r dL = L2 L1 = L t1 L1
(3)力对任意点的力矩，在通过该点的任一轴上的投影， (3)力对任意点的力矩，在通过该点的任一轴上的投影， 力对任意点的力矩 等于该力对该轴的力矩。 等于该力对该轴的力矩。 例2：圆锥摆球在水平面内匀速转 ： A r 分别讨论对固定点A和 点 动，分别讨论对固定点 和O点， r Lo T θ 小球受的张力矩，重力矩和角动量。 小球受的张力矩，重力矩和角动量。 LA R v v v 对于A点 解： 对于 点 MA = R ×T r O v v v = mgR sin θ = mgr Mg = R×mg mg v v v LA = R×mv

角动量定理角动量守恒定律

应用牛顿第二定律
在系统整体上应用牛顿第二定律，得到系统受到的合外力矩为零时 的角动量守恒条件。
推导角动量守恒定律
根据系统总角动量和角动量守恒的条件，推导出角动量守恒定律， 即在合外力矩为零时，系统总角动量保持不变。
推导过程中的注意事项与难点解析
注意事项
在推导过程中，需要注意定义和计算过程中的符号约定，以及正确应用牛顿第二 定律。
角动量定理与守恒定律的适用范围
角动量定理适用于描述物体在受到外 力矩作用下的旋转运动，特别是需要 分析力矩对旋转运动的影响时。
角动量守恒定律适用于描述某些特定 条件下物体的旋转运动，如系统不受 外力矩作用或系统内力的力矩相互抵 消等。
04
角动量定理与守恒定律的 推导过程
角动量定理的推导过程
定义角动量
03
角动量守恒定律则是在一定条件下，物体的角动量保持不变 。
角动量定理与守恒定律的区别
角动量定理是一个运动方程，用于描 述旋转运动的物体在外力矩作用下的 运动规律，而角动量守恒定律则是一 个守恒条件，用于描述某些特定情况 下旋转运动的物体角动量的保持。
VS
角动量定理是一个瞬时规律，关注的 是物体在某一时刻的运动状态，而角 动量守恒定律则是一个时间平均规律， 关注的是物体在一段时间内的平均运 动状态。
矩作用会导致旋转物体角动量的增加或减少。
02
揭示旋转运动的本质
角动量定理阐明了旋转运动的本质特征，即旋转物体的角动量是守恒的，
但可以通过力矩作用进行改变。
03
指导设计旋转机械
角动量定理在旋转机械设计和运行中具有指导意义，例如在电动机、发
电机、陀螺仪等设备的设计中，需要考虑力矩作用和角动量的变化。
角动量守恒定律的物理意义

大学课件角动量定理


3-6 角动量定理
L mR2 ( 2g sin )1 2
R
第三章 守恒定律
8
系一小球放在桌面上，另一端用手缓慢拉绳，
开始时小球绕孔运动，半径为r1 ， 速率为 v1 ， 当半径变为r2 时，
f拉பைடு நூலகம்
0 v1
r2
r1
求小球的速率v2
解：小球受力：f 拉
L2 L1
L2 L1
r1mv1 r2mv2
v2
r1 r2
v1
第三章 守恒定律
6
大学
物理
例 一半径为 R 的光滑圆环置于
3-6 角动量定理
竖直平面内. 一质量为 m 的小球
穿在圆环上, 并可在圆环上滑动.
小球开始时静止于圆环上的点 A
(该点在通过环心 O 的水平面上)，
然后从 A点开始下滑．设小球与
圆环间的摩擦力略去不计．求小
球滑到点 B 时对环心 O 的角动量
和角速度．
解 小球受力 P 、FN 作用, FN 的力矩为零，重力矩垂直
· 3.6.2 dL
质点的角动量定理
dr
p
dr
p
r
dp
dt
式中 dr
p
dt
v
p
dt
0
dt
dt dp F dt
定义：外力 F 对参考点O的力矩 M
r
O
F
M r0
r
dL dt
•mF
r
F
力矩的大小： M rF sin r0F
dL M dt
dL Mdt
t
2
M
t1
dt
L2
L1
质点对某一参考点的角动量随时间的变化率等于质点所 受的合外力对同一参考点的力矩。

角动量 角动量定理


d M (r P) dt
定义： L r P ——角动量
——角动量定理
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理
3
作用在质点上的力矩等于质点角动量对时间的变化率。 此即质点对固定点的角动量定理。

t
t0
Mdt L L0

t
t0
Mdt
叫冲量矩
2–5 角动量 角动量定理
2
2 质点的角动量定理
M r F
dP F dt
dP d dr M r (r P) P dt dt dt
P mv
dr v dt
dL M dt
dr P v mv 0 dt
角动量
1. L r P
L 的方向符合右手法则.
L m vrsin
第2章 运动定律与力学中的守恒定律
z L mv

r
2–5 角动量 角动量定理
4
2.质点在垂直于 z 轴平面
上以角速度
作半径为 r
的圆运动，相对圆心
z

o r
90
A
L r p r mv
mv0 (m M )v1
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量定理
9
在由A→B的过程中，子弹、木块系统机械能守恒
1 1 1 2 2 (m M) v 1 (m M) v 2 k (l l0 ) 2 2 2 2
在由A→B的过程中木块在水平面内只受指向O点的 弹性有心力，故木块对O点的角动量守恒，设 v2 与OB方向成θ角，则有

角动量定理公式

角动量定理公式
牛顿第二定律描述了物体运动的基础定律，牛顿第二定律表明物体在受到力的作用下，它的运动对外界力具有相应的反应，即保持状态不变就是物体不会自动移动。

牛顿第二定律从另一个方面更好地描述了物体运动，即角动量定理：物体运动时，角动量是保持不变的，即角动量守恒定律。

角动量定理定义为：质点系统在任何时刻的角动量是一个守恒量，不会受外界的改变而改变，即不会由于内部及外部的力而改变。

用数学符号表示该定理就是：L=L0。

其中，L表示物体角动量的量，L0表示同一时刻物体的总的角动量的初始量。

角动量定理在实际应用中也具有重要的意义，可以说物体的角动量是物体运动的重要参数，在实际的机械应用中神经元行为被证明物体上外力对物体角动量的作用在该定理中得到了完整的描述和表现。

推广一下角动量定理，我们可以证明角动量定理从力学基础的角度阐述的不仅是物体的状态，也表明了在物体运动中，物体的局部运动状态会受到整体运动的限制，这也是物体的自身结构所决定的，角动量定理也完整地反映了这一点。

在实际应用中，角动量定理可以帮助我们快速解决物体运动的相关问题，有助于精确描述物体运动及其受外力影响时形成的物理参数变化，也可以提高计算机实现物体运动模拟的准确率。

总之，角动量定理是物体运动学中一个非常关键的定理，对于探究物体运动的机理和运动规律有重要的意义。

它的应用可以顺利解决很多实际中存在的问题，也可以提升模拟物体运动的精度。

角动量定理是物理定律研究中最为重要的一个定理，它更好地描述了物体运动，为研究物体运动提供了重要的线索。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
求:人和车各自相对地面移动的距离。
解:设人速为u,车速为v。以地面为参考系。
系统在水平方向上动量守恒 ， u
v
Mv+
mu=
0
v
m M
u
x
t
t0
vdt
m M
t
t0
udt
x车地
m M
x人地
x人地 x人车 x车地
x人车 L
Δx人地
ML Mm
Δ x车地
–
mL M m
3、质量流动问题 （有质量流入与流出） 可用动量定理与动量守恒定律来处理。
非惯性系类型不同, 惯性力的表达式不同。
怎么办?
a0
a0m
没问题！
F 0
a球 0
惯性力
R ma0
例3、一光滑的劈，质量为 M ，斜面倾角为 ，并位于
光滑的水平面上，另一质量为 m 的小块物体，沿劈的斜 面无摩擦地滑下， 求劈对地的加速度。
a2
m
M
a1 解：以研设劈究Mm为对对对参象M地照：的的系m加加，、速速建M度度立坐aa21标如图。
速平动参考系。物体除受重 力和斜面的支承力外，还受 到惯性力的作用，如图所示。
设物体沿斜面下滑的加速
r
ma0
rN S
a0
a
mgr h
度为a ,则在平行于斜面的方向上有:
mg sin ma0sin ma
mg sin ma0sin ma
a (g a0)sin
物体沿斜面作匀加速直线运动，
故
若
F合外
0
则 Pi 恒矢量
F1外
注意：（（12））若条件F合F外 合外
0 。(系统所受内力很大，外力可以忽略不计)
0 但 F合外x 0 则 Pix 恒量
（3）普遍适用（高低速、宏微观）。
例3. 水平光滑冰面上有一小车,长度为L,质量为 M。车的一端有一质量为m的人,人和车原 来均静止。若人从车的一端走到另一端,
大学物理 电子教案
(力学3)
3、非惯性系中的力学方程 惯性力
非惯性系中，物体除了受到由相互作用产生的力
（牛顿力）外，还受到由非惯性系加速引起的附加力
称惯性力。
F牛
顿力
R惯性力
ma'
物体相对于非惯性系的加速度
下面只介绍加速平动参考系中惯性力
惯性力
R ma0
R的形式：
加速平动参考系相对于惯性系的加速度
为估算冲力的大小带来方便。
引入平均冲力 F
t2
t1
F
(t )dt
F
(t2
t1
)
则:
F
t2
t1
F
(t
)dt
P2
P1
t2 t1
t2 t1
例1. 设机枪子弹的质量为50g,离开枪口时的速度
为800m/s。若每分钟发射300发子弹，求射手
肩部所受到的平均压力。
解: 根据动量定理
F
t2
t1
F (t )dt
dt
t1
P2ddPt
P1
Fdt dP
微分形式
t2F dt
t1
P2
P1
积分形式
设在时间间隔dt 内，质点所受的力为 F ，
为 F在则dt称时间dI内作F用dt在质点上的冲量。
若质点受力的持续作用， 时间由 t1 t2
I
t2 t1
Fdt
(力的时间累积效应)
动量定理：冲量等于动量的增量。
I
t2
mv(v v0 ) l
2.0300(3000) 6.0105 N 0.3
质点系(推导自学):
t2 t1
F合
外dt
i
Pi 2
i
Pi1
质点系的动量定理：系统在某一段时间内 所受合外力的总冲量等于在同一段时间内
F3外
系统的总动量的增量。
m1•
2、动量守恒定律
•
•m3
内 力
m2
F2外
等效原理：
引力作用与惯性力作用等效。
匀加速运动的非惯性系等效于一个均匀恒定的引力场。
mg
引力
地面
a g
mg
惯性力
太空中
R
mg
g
失重
mg
地面
可知：（1）利用加速系统人造一个引力场。 （2）利用加速系统抵消一个引力场。
（二）动量定理与守恒定律
1、动量定理 一个质点：F
dP
冲量
t2
F
h
sin
S
1 2Βιβλιοθήκη at21 2
(
g
a0
)sin
t2
r
ma0
rN a
S
mgr
a0
h
则物体滑到斜面末端所需的时间为:
t
1
sin
2h g a0
1 sin 30
21 9.8 1.8
1s
问：惯性力是虚拟的力还是真实的力？
有争论！ 力的定义 （1）力是物体间的相互作用。
（2）力使物体运动状态发生变化。
爱因斯坦广义相对论建立基础之一
P2
P1
t2 t1 t2 t1
射手肩部所受到的平均压力为
F FPttmtmvv
300 0.05800 200N 60
例2.飞机以v=300m/s(即1080 km/h)的速度飞行,撞
到一质量为m=2.0kg的鸟,鸟的长度为l＝0.3 m。
假设鸟撞上飞机后随同飞机一起运动, 试估算
它们相撞时的平均冲力的大小。
y,
aR21 x,
N1
mg
受力分析：如图
y
N2
R2
a1
x
Mg
N
' 1
y,
aR21 x,
运动方程：
N1
mg
y
N2 R2
Mg
N
' 1
a1
x
m对M
对m： x, : mg sin R1 cos ma 2 (1)
y, : mg cos N1 R1 sin 0 (2)
对M： x :
N
' 1
s
in
R2
Ma1
0 (3)
y
:
N2
N
' 1
cos
Mg
0
(4)
M对M
（将动力学问题化作静力学问题处理
达朗贝尔原理）
R1 R1
R2
将
N
' 1
N1,
R1
ma1,
R2 Ma1
代入（2）（3）
N1 mgcos ma1sin N1 sin Ma1
m sin cos a1 M m sin2 g M对地
附：将上式代入（1）得
m对M：
(M m)sin a2 M m sin2 g
ma对地a：1 a2
例4、 升降机以加速度a0=1.8m•s -2下降。升降机内
有一与地板成 30角的光滑斜面,一物体从
斜面顶端由相对静止下滑。设斜面顶端离地
板高h=1m。求物体滑到斜面末端所需的时间。
解：选升降机为参考系，它是加
解: 以地面为参考系, 把鸟看作质点,因鸟的速度远 小于飞机的, 可将它在碰撞前的速度大小近似 地取为v0=0 m/s, 碰撞后的速度大小v＝300m/s。
由动量定理可得 mv mv0 I Ft
碰撞经历的时间就取为飞机飞过鸟的长度
l的距离所需的时间，则:
F
mv mv0
t
mv mv0 l/v
t1
Fdt
P2
P1
注意：（1）动量定理适用于惯性参考系。在非惯 性系中还须考虑惯性力的冲量。
（2）动量定理常用于碰撞和打击问题。在这 些过程中，物体相互作用的时间极短，但力却很大 且随时间急剧变化。这种力通常叫做冲力 。
t2
t1
Fdt
P2
P1
冲力的瞬时值很难确定，但在过程的始末两
时刻,质点的动量比较容易测定, 所以动量定理可以