数学人教版九年级上册圆的切线证明与计算

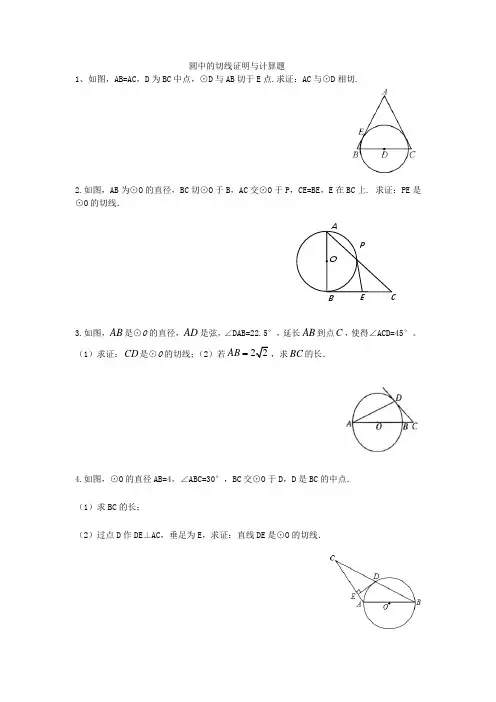
圆中的切线证明与计算题1、如图，AB=AC ，D 为BC 中点，⊙D 与AB 切于E 点.求证：AC 与⊙D 相切.2.如图，AB 为⊙O 的直径，BC 切⊙O 于B ，AC 交⊙O 于P ，CE=BE ，E 在BC 上. 求证：PE 是⊙O 的切线．3.如图，是⊙O 的直径，是弦，∠DAB=22.5°，延长到点，使得∠ACD=45°。

（1）求证：是⊙O 的切线；（2）若，求的长．4.如图，⊙O 的直径AB=4，∠ABC=30°，BC 交⊙O 于D ，D 是BC 的中点． （1）求BC 的长；（2）过点D 作DE ⊥AC ，垂足为E ，求证：直线DE 是⊙O 的切线．AB AD AB C CD 22AB BC OABPE C5.如图,已知A 是⊙O 上一点,半径OC 的延长线与过点A 的直线交于B 点,OC=BC,AC=OB 21. （1）求证:AB 是⊙O 的切线；（2）若∠ACD=450，OC=2,求弦CD 的长.6.如图，在Rt △ABC 中，∠B=90°，∠BAC 的平分线交BC 于点D ，E 为AB 上的一点，DE=DC ，以D 为圆心，DB 长为半径作⊙D ，AB=5，EB=3. （1）求证：AC 是⊙D 的切线; （2）求线段AC 的长.7.如图，在两个同心圆⊙O 中，大圆的弦AB 切小圆于点C. （1）求证：AC=BC;（4分）（2）若AB=8，求两圆之间圆环的面积(结果保留Π).(4分)8.如图，在⊙O中，弦BC⊥半径OA于点D，点F是CD上一点，AF交⊙O于点E，点P为BC延长线上一点，PF=PE.（1）求证：PE是⊙O的切线;(3分)（2)若AD=2,BC=8，DF=1，求PE的长.(5分)9.如图，在Rt△ABC中，∠ABC＝90°，∠BAC的平分线交BC于D，以D为圆心，DB长为半径作⊙D，求证：AC与⊙D相切．10.如图，在△ABC中，AB＝AC，以AB为直径的⊙O与边BC交于D，与边AC交于E，过D作DF AC于F.（1）求证：DF为⊙O的切线；（2）若DE AB＝5，求AE的长.11.如图，在△ABC中，AB＝AC，以边AB为直径作⊙O，交BC于D，过D作DE⊥AE. （1）求证：DE是⊙O的切线；（2）连接OC，若∠CAB＝120︒，求DEOC的值.12.如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M，与AB、AD分别相交于点E、F.求证：CD与⊙O相切.13.如图，AB为⊙O的直径，C为⊙O上一点，D是BC的中点，DE⊥AB于E，I是△ABD的内心，DI的延长线交⊙O于N.（1）求证：DE是⊙O的切线；（2）若DE＝4，CE＝2，求⊙O的半径和IN的长.14.如图，在△ABC中，AB＝AC，I是△ABC的内心，⊙O交AB于E，BE为⊙O的直径. （1）求证：AI与⊙O相切；（2）若BC＝6，AB＝5，求⊙O的半径.=，点M为BC上一点，且CM＝AC.15．如图，AB是⊙O的直径，AC CE（1）求证：M为△ABE的内心；（2）若⊙O的半径为5，AE＝8，求△BEM的面积.16.如图，AB＝AC，点O在AB上，⊙O过点B，分别交BC于D、AB于E，DF⊥AC. （1）求证：DF为⊙O的切线；（2）若AC切⊙O于G，⊙O的半径为3，CF＝1，求AC.。

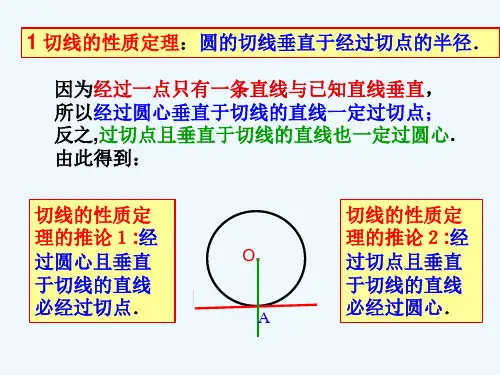
中考数学与圆的切线相关的证明与计算圆的切线：经过半径的外端并且垂直于这条半径的直线是圆的切线 .一、圆的切线的判定及相关计算1.如图，以△ABC 的边AB 为直径作⊙O，与BC 交于点D，点E 是弧BD 的中点，连接AE 交BC 于点F，∠ACB＝2∠BAE .求证：AC 是⊙O 的切线．例题1图【分析】连接AD，利用等弧所对圆周角相等及∠ACB＝2∠BAE 可得到∠BAD＝∠BCA，再结合直径所对圆周角为直角即可得证．证明：如解图，连接AD.例题1解图∵点E 是弧BD 的中点，∴弧BE ＝弧DE，∴∠1＝∠2 .∵∠BAD＝2∠1, ∠ACB＝2∠1，∴∠ACB＝∠BAD.∵AB为⊙O 直径，∴∠ADB＝∠ADC＝90°.∴∠DAC＋∠C＝90°.∵∠C＝∠BAD，∴∠DAC＋∠BAD＝90°.∴∠BAC＝90°，即AB⊥AC. 又∵AB 是⊙O 的直径，∴AC 是⊙O 的切线．证明切线的常用方法：1．直线与圆有交点，“连半径，证垂直”．(1) 图中有90°角时，证垂直的方法如下：①利用等角代换：通过互余的两个角之间的等量代换得证；②利用平行线性质证明垂直：如果有与要证的切线垂直的直线，则证明半径与这条直线平行即可；③利用三角形全等或相似：通过证明切线和其他两边围成的三角形与含90°的三角形全等或相似得证．(2)图中无90°角时：利用等腰三角形的性质，通过证明半径为所在等腰三角形底边的中线或角平分线，再根据“三线合一”的性质得证．2．直线与圆无交点，“作垂线，证相等”．2.如图，在Rt△ABC 中，∠C＝90°，⊙O 是△ABC 的外接圆，点D 在⊙O 上，且弧AD＝弧CD , 过点D 作CB 的垂线，与CB 的延长线相交于点E，并与AB 的延长线相交于点F .(1) 求证：DF 是⊙O 的切线；(2) 若⊙O 的半径R＝5，AC＝8，求DF 的长．例题2图【解析】(1) 证明：如解图，连接DO 并延长，与AC 相交于点P.例题2解图∵弧AD = 弧CD，∴DP⊥AC.∴∠DPC＝90°.∵DE⊥BC，∴∠CED＝90°.∵∠C＝90°.∴∠ODF＝90°，而点D 在⊙O 上，∴DF 是⊙O 的切线；(2) 解：例题2解图∵∠C＝90°，R＝5，∴AB＝2R＝10.在Rt△ABC 中，根据勾股定理可得，BC＝6 .∵∠DPC＋∠C＝180°，∴PD∥CE.∴∠CBA＝∠DOF.∵∠C＝∠ODF，∴△ABC ∽△FOD.∴CA / DF = BC / OD , 即8 / DF = 6 / 5 ,∴DF = 20 / 3 .类型二、切线性质的相关证明与计算3.如图，AB 是⊙O 的直径，AC 是⊙O 的弦，过点B 作⊙O 的切线DE，与AC 的延长线交于点D，作AE⊥AC 交DE 于点E .(1) 求证：∠BAD＝∠E；(2) 若⊙O 的半径为5，AC＝8，求BE 的长．例题3图【解析】(1) 证明：∵⊙O 与DE 相切于点B，AB 为⊙O 的直径，∴∠ABE＝90°.∴∠BAE＋∠E＝90°.又∵∠DAE＝90°，∴∠BAD＋∠BAE＝90°.∴∠BAD＝∠E；(2) 解：如解图，连接BC.例题3解图∵AB 为⊙O 的直径，∴∠ACB＝90°，∵AC＝8，AB＝2 ×5＝10 .∴在Rt△ACB 中，根据勾股定理可得BC = 6 .又∵∠BCA＝∠ABE＝90°，∠BAD＝∠E，∴△ABC ∽△EAB .∴AC / EB = BC / AB , 即8 / EB = 6 / 10 ,∴BE＝40 / 3 .4.如图，⊙O 的半径OA＝6，过点A 作⊙O 的切线AP，且AP＝8，连接PO 并延长，与⊙O交于点B、D，过点B 作BC∥OA，并与⊙O 交于点C，连接AC、CD.(1) 求证：DC∥AP；(2) 求AC 的长．例题4图【解析】(1) 证明：∵AP 是⊙O 的切线，∴∠OAP＝90°.∵BD 是⊙O 的直径，∴∠BCD＝90°.∵OA∥CB，∴∠AOP＝∠DBC，∴∠BDC＝∠APO.∴DC∥AP；(2) 解：∵AO∥BC，OD＝OB，例题4解图∴如解图，延长AO 交DC 于点E，则AE⊥DC，OE＝1/2 BC，CE＝1/2 CD.在Rt△AOP 中，根据勾股定理可得：OP＝10.由(1) 知，△AOP∽△CBD，∴BD/OP = BC/OA = CD/AP , 即12/10 = BC/6 = DC/8 ,∴BC = 36/5 , DC = 48/5 .∴OE = 18/5 , CE = 24/5 , AE = OA + DE = 6 + 18/5 = 48/5 ,在Rt△AEC 中，根据勾股定理可得：AC = 24√5 / 5 .5.如图，AC 是⊙O 的直径，AB 是⊙O 的一条弦，AP 是⊙O 的切线．作BM＝AB，并与AP 交于点M，延长MB 交AC 于点E，交⊙O 于点D，连接AD.(1) 求证：AB＝BE；(2) 若⊙O 的半径R＝5，AB＝6，求AD 的长．例题5图【解析】(1) 证明：∵AP 是⊙O 的切线，∴∠EAM＝90°，∴∠BAE＋∠MAB＝90°，∠AEM＋∠AME＝90°. 又∵AB＝BM，∴∠MAB＝∠AMB，∴∠BAE＝∠AEB，∴AB＝BE；(2) 解：如解图，连接BC.例题5解图∵AC 是⊙O 的直径，∴∠ABC＝∠EAM＝90°，在Rt△ABC 中，AC＝10，AB＝6，根据勾股定理可得：BC = 8 . 由(1) 知，∠BAE＝∠AEB，∴△ABC∽△EAM，∴∠C＝∠AME，AC/EM = BC/AM , 即10/2 = 8/AM ,∴AM = 48/5 .又∵∠D＝∠C，∴∠D＝∠AMD.∴AD＝AM＝48/5 .。

人教版数学九年级上册24.2.2.2《切线的判定和性质》说课稿一. 教材分析《切线的判定和性质》是人教版数学九年级上册第24章《圆》的第二个知识点。

本节内容是在学生已经掌握了圆的定义、性质以及圆的基本运算的基础上进行学习的。

本节内容主要介绍了切线的定义、判定和性质，以及切线与圆的位置关系。

这些知识对于学生理解和掌握圆的性质，解决与圆有关的问题具有重要意义。

二. 学情分析九年级的学生已经具备了一定的数学基础，对于圆的性质和运算已经有了一定的了解。

但是，对于切线的定义、判定和性质以及切线与圆的位置关系可能还比较陌生。

因此，在教学过程中，我需要注重引导学生从已知的圆的性质出发，推导出切线的性质，从而帮助学生理解和掌握切线的相关知识。

三. 说教学目标1.知识与技能目标：使学生理解和掌握切线的定义、判定和性质，以及切线与圆的位置关系。

2.过程与方法目标：通过观察、思考、讨论和操作，培养学生的观察能力、逻辑思维能力和动手操作能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养学生的团队合作意识和自主学习能力。

四. 说教学重难点1.教学重点：切线的定义、判定和性质，以及切线与圆的位置关系。

2.教学难点：切线的判定和性质的推导过程，以及切线与圆的位置关系的理解。

五. 说教学方法与手段在本节课的教学中，我将采用讲授法、引导发现法、小组合作学习和动手操作相结合的教学方法。

同时，利用多媒体课件和几何画板等教学手段，帮助学生直观地理解切线的性质和判定。

六. 说教学过程1.导入：通过复习圆的性质，引导学生思考与圆有关的问题，激发学生的学习兴趣。

2.引导发现：引导学生从已知的圆的性质出发，观察和思考切线的性质，引导学生发现切线的判定和性质。

3.讲解与示范：讲解切线的定义、判定和性质，以及切线与圆的位置关系，并通过几何画板进行演示。

4.动手操作：让学生利用几何画板或者手工画图，自己尝试作出圆的切线，并判断其性质。

5.小组合作学习：让学生分组讨论，总结切线的性质和判定，以及切线与圆的位置关系。

切线的概念、切线的判定和性质-人教版九年级数学上册教案一、切线的概念1. 切线的定义在圆上取一点P，连接P与圆心O，若通过点P的直线与圆相交于点P，则这条直线称为该圆在点P处的切线。

2. 切线的性质切线只与圆相交于切点，且垂直于半径。

二、切线的判定1. 判定方法1在圆上任取一点P，连接P与圆心O。

若连接P与圆心O的线段与已知直线L 垂直，则L与圆的交点就是切点，而L即为此点处的切线。

2. 判定方法2在圆上任取一点P，连接P与圆心O。

作过点P并与已知直线L平行的直线，与圆相交于点Q。

再连接点Q与圆心O，则Q与L的交点即为圆在点P处的切点，L即为点P处的切线。

三、切线性质的应用1. 切线定理若一条直线与圆相交于点A、B，则与这条直线垂直的切线分别过点A、B。

2. 判定定理在圆上任取两点P、Q，以这两点为端点连一条线段，若该线段平分圆周角，则它的延长线必过圆的圆心。

3. 弦割定理两条互相垂直的弦互相垂直。

4. 弦长定理两条互相垂直的弦所对圆周的两段弧相等。

5. 弧上点角定理圆周上一点的任意两个角所对的弧长相等。

四、练习题1.已知圆O，半径为3.4cm，P为圆上一点，PA为一条直线，且PA=8.1cm。

求PA的垂线与OP的夹角。

2.已知圆的直径是20cm，D,E,F,G均在圆上。

若DE⊥FG，DE=12cm，FG=9cm，求DG的长。

3.已知圆心角ACB的弧度是20度，线段AB上一点D是圆上的一点，求角ADC的角度。

五、课堂小结1.切线的定义和性质。

2.切线判定方法和定理。

3.切线性质的应用。

4.练习题的解答。

六、作业1.完成课堂练习题。

2.独立思考，将切线定理、判定定理、弦割定理、弦长定理和弧上点角定理的证明写出来。