控制理论作业二答案
- 格式:doc
- 大小:1.30 MB
- 文档页数:17

2024年化工自动化控制仪表作业证理论考试练习题I、(判断题)在带定位罂的谢节阀校验中,应该先校调节阀,在与定位器联校。
参考答案:正确2,(判断题)串联电路中,电路两端的总电压等于各电阻两端的分压之和。
参考答案:正确3、(判断题》请判断下列SIMATICS7∙300系列P1.C中的模板的安装顺序是否正确。
电源模板、CPU、扩展模板、信号模板、通讯模板、功能模板。
参考答案:错误4、(判断题)某压缩机出口压力为450KPa,实际操作时最大允许有±12.6Kpa的测量误差,那么选用用力表的量程和精度等级各是675KPa:1.5级。
参考答案:错误5、(判断题)我们常讲的紧急停车系统(ESD),安全联锁系统(SlS).仪表保护系统(IPS)、故障安全控制系统(FSC)均可称为安全仪表系统(SIS).参考答案:正确6、(判断题)干扰通道的放大系数尽可能大些,时间常数於可能小些,干扰作用点尽出第近调节阀,加大对象干扰通道的容责滞后,使干扰对被控变圻的影响减小.参考答案:错误7、(判断题)蝶阀特点是结构荷单、流阻小,泄漏量大,适用于口径较大、大流量、低压差的场合。
参考答案:正确8、(判断即)西门子S7-300系列P1.C,不可以带电更换模板、卡件。
参考答案:正确9、(判断题)苛性钠和它的溶液遇火既不会燃烧又不能助燃。
参考答案:错误10,(判断题)国标规定:调节阀在1.1倍公称压力下,填料至上、下阀盖连接处不应有渗漏现象,在1.5倍公称压力卜.,持续3mn以上时间,其法体不应有肉眼可见的渗漏。
参考答案:错误20、(判断题)当阀体直立,阀杆卜.移时,阀芯与阀座间的流通面积减小的称为正装。
参考答案:正确21、(判断题)CENTUMCS3000系统中.回路的报警状态显示为HH,这意味着该回路的PV值过高,发生了高高报警。
参考答案:正确22、(判断题)在电路中,通常把参考点的电位规定为零电位。
参考答案:正确23、(判断题)空气过滤质压器是最典型的附件,它用于净化来自空气压缩机的气源,并能把压力调整到所需的压力值,具有自动稳压的功能,参考答案:正确24、(判断题)可编程序控制器采用循环扫描工作方式,这种工作方式可以避免继电器接触控制的触点竞争和时序失配问题•参考答案:正确25、(判断题)化工装置内的常温设备管道同样需要保温.参考答案:错误26、(判断即)比值控制系统确定主动量的原则是在生产过程中起主导作用、可测不可控、且较为昂贵的物料流量一般为主动量。
![地大《现代控制理论》在线作业二[60467]](https://uimg.taocdn.com/e1976da4b307e87100f6969d.webp)
地大《现代控制理论》在线作业二
一、单选题
1.保证稳定是控制系统正常工作的必要前提,对受控系统通过反馈使其极点均具有负实部,保证系统渐近稳定称为()。
A.能控性
B.能观性
C.系统镇定
D.稳定性
答案:C
2.对于能控能观的线性定常连续系统,采用静态输出反馈闭环系统的状态()。
A.能控且能观
B.能观
C.能控
D.以上三种都有可能
答案:A
3.对于同一个系统,可有()个状态空间表达式。
A.1个
B.2个
C.3个
D.无穷多个
答案:D
4.由状态空间模型导出的传递函数()。
A.惟一
B.不惟一
C.无法判断
D.皆有可能
答案:A
5.维数和受控系统维数相同的观测器为()。
A.降维观测器
B.全维观测器
C.同维观测器
D.以上均不正确
答案:B
6.根据线性二次型最优控制问题设计的最优控制系统一定是()的。
A.渐近稳定
B.稳定
C.一致稳定
D.一致渐近稳定
答案:A
7.下列语句中,正确的是()。
A.系统状态空间实现中选取状态变量是唯一的,其状态变量的个数也是唯一的
B.系统状态空间实现中选取状态变量不是唯一的,其状态变量的个数也不是唯一的。
第九章 线性系统的状态空间分析与综合9-1 设系统的微分方程为u x x x=++23 其中u 为输入量,x 为输出量。
⑴ 设状态变量x x =1,xx =2,试列写动态方程; ⑵ 设状态变换211x x x +=,2122x x x --=,试确定变换矩阵T 及变换后的动态方程。
解:⑴ u x x x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡1032102121 ,[]⎥⎦⎤⎢⎣⎡=2101x x y ; ⑵ ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2121x x T x x ,⎥⎦⎤⎢⎣⎡--=2111T ;⎥⎦⎤⎢⎣⎡--=-11121T ;AT T A 1-=,B T B 1-=,CT C =; 得,⎥⎦⎤⎢⎣⎡--=2111T ;u x x x x ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡1110012121 ,[]⎥⎦⎤⎢⎣⎡=2111x x y 。
9-2 设系统的微分方程为u y y yy 66116=+++ 其中u 、y 分别系统为输入、输出量。
试列写可控标准型(即A 为友矩阵)及可观标准型(即A 为友矩阵转置)状态空间表达式,并画出状态变量图。
解:可控标准型和可观标准型状态空间表达式依次为,[]x y u x x 0061006116100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---= ;[]xy u x x 1000066101101600=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---= ; 可控标准型和可观标准型的状态变量图依次为,9-3 已知系统结构图如图所示,其状态变量为1x 、2x 、3x 。
试求动态方程,并画出状态变量图。
解:由图中信号关系得,31x x= ,u x x x 232212+--= ,32332x x x -= ,1x y =。
动态方程为 u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=020********* ,[]x y 001;状态变量图为9-4 已知双输入双-输出系统状态方程和输出方程23213213212161162u x x x xu u x xu x x+---=-+=+= ,32122112x x x y x x y -+=-=, 写出其向量-矩阵形式并画出状态变量图。


第三章3-1 已知二阶系统闭环传递函数为 369362++=s s G B。
试求单位阶跃响应的t r , t m ,δ% , t s 的数值?解:[题意分析]这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n ω参数,而后把n ω代入性能指标公式中求出r t ,m t ,%δ,s t 和N 的数值。
上升时间 t r 峰值时间t m 过度过程时间t s 超调量δ%3-2 设单位反馈系统的开环传递函数为试求系统的性能指标,峰值时间,超调量和调节时间。
解:[题意分析]这是一道给定了开环传递函数,求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数(ζ,n ω)的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为与二阶系统传递函数标准形式2222nn ns s ωζωω++相比较可得12,12==n n ζωω,即n ω=1,ζ=0.5。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为3-3 如图1所示系统,假设该系统在单位阶跃响应中的超调量%δ=25%,峰值时间m t =0.5秒,试确定K 和τ的值。
K,τ与ζ,n ω的关系;δ联系起来。
由系统结构图可得闭环传递函数为 与二阶系统传递函数标准形式相比较,可得由题目给定: %25%100%21=⨯=--ζζπδe即 25.021=--ζζπe两边取自然对数可得 依据给定的峰值时间: 5.012=-=ζωπn mt (秒)所以 85.615.02=-=ζπωn (弧度/秒)故可得τ≈0.13-4 已知系统的结构图如图2所示,若)(12)(t t x ⨯= 时,试求: (1) 当τ=0时,系统的t r , t m , t s 的值。
(2) 当τ≠0时,若使δ%=20%,τ应为多大。
可得 )/(07.750秒弧度==n ω由于ss X 2)(=输出的拉氏变换为 则拉氏反变换为(2) 当τ≠0时,闭环传递函数由 %20%100%21=⨯=--ζζπδe两边取自然对数 61.12.0ln 12-==--ζζπ, 可得故 73.85.)107.746.0(2=-⨯=o τ3-5(1) 什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。



西交《自动控制理论》在线作业
试卷总分:100 得分:100
一、多选题(共13 道试题,共39 分)
1.关于传递函数正确的说法有( )
A.传递函数的分母与系统的输入无关
B.传递函数分母中s的阶次不小于分子中s的阶次
C.传递函数是无量纲的
D.不同物理类型的系统,可以具有相同形式的传递函数
E.在零初始条件下,系统输出的拉氏变换取决于输入和其传递函数答案:ABDE
2.选取输入信号应当考虑以下几个方面()。
A.典型
B.简单
C.复杂
D.能使系统在最恶劣的情况下工作
答案:ABD
3.带宽越大,快速性与过渡过程的上升时间有何特点。
()
A.快速性越好
B.上升时间越小
C.上升时间越大。

第三章3-1 已知二阶系统闭环传递函数为 369362++=s s G B 。
试求单位阶跃响应的t r , t m ,δ% , t s 的数值?解:[题意分析]这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n ω参数,而后把n ω代入性能指标公式中求出r t ,m t ,%δ,s t 和N 的数值。
上升时间 t r峰值时间t m 过度过程时间t s 超调量δ%3-2 设单位反馈系统的开环传递函数为试求系统的性能指标,峰值时间,超调量和调节时间。
解:[题意分析]这是一道给定了开环传递函数,求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数(ζ,n ω)的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为与二阶系统传递函数标准形式2222nn n s s ωζωω++相比较可得12,12==n n ζωω,即n ω=1,ζ=0.5。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为3-3 如图1所示系统,假设该系统在单位阶跃响应中的超调量%δ=25%,峰值时间m t =0.5秒,试确定K 和τK,τ与ζ,n ω的关系;%δ,m t 与ζ,nω 由系统结构图可得闭环传递函数为 与二阶系统传递函数标准形式相比较,可得由题目给定: %25%100%21=⨯=--ζζπδe即 25.021=--ζζπe两边取自然对数可得 依据给定的峰值时间: 5.012=-=ζωπn m t (秒)所以 85.615.02=-=ζπωn (弧度/秒)3-4 已知系统的结构图如图2所示,若)(12)(t t x ⨯= 时,试求:(1) 当τ=0时,系统的t r , t m , t s 的值。
(2) 当τ≠0时,若使δ%=20%,τ应为多大。
求出可得 )/(07.750秒弧度==n ω 由于ss X 2)(=输出的拉氏变换为 则拉氏反变换为(2) 当τ≠0时,闭环传递函数由 %20%100%21=⨯=--ζζπδe两边取自然对数 61.12.0ln 12-==--ζζπ, 可得故 73.85.)107.746.0(2=-⨯=o τ3-5(1) 什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。

、单选题(共40道试题,共80分。
V欠阻尼二阶系统的令叫都与c )1匚有关 B.超无关C* □有关D. fp无关A.B.* C.D.满分:2分2.适合于应用传递函数描述的系统是()A.非线性定常系统B.线性时变系统* C.线性定常系统D.非线性时变系统满分:2分3.最小相角系统闭环稳定的充要条件是()* A.奈奎斯特曲线不包围(-1,jO )点B.奈奎斯特曲线包围(-1,jO )点C.奈奎斯特曲线顺时针包围(-1,jO )点D.奈奎斯特曲线逆包围(-1,jO )点4.二阶系统的闭环增益加大()A.快速性越好,■■■■'I B.超调量越大厂C.峰值时间提前忖D.对动态性能无影响满分:2分欠阻尼二阶系统的務叫,都与()5直-"J有关 B. b%无关 C.—有关乩S无关C A.B.护C.厂D.满分:2分6.某系统单位斜坡输入时务二叫说明该系统<〉* A.是0型系统'B.闭环不稳定「C.闭环传递函数中至少有一个纯积分环节厂D.幵环一定不稳定满分:2分冈环系统幅频特性如图所乎;则系统带宽频率是!)'、理比® C・D.佟0? 1-闭环幅频特性满分:2分8.讨论系统的动态性能时,通常选用的典型输入信号为()忖A.单位阶跃函数B.单位速度函数厂C.单位脉冲函数第I D.单位加速度函数满分:2分9.二阶系统的闭环增益加大()A.快速性越好'B.超调量越大C.峰值时间提前炖D.对动态性能无影响满分:2分单位反愦最彳湘角系统的开环对数频率特性如圄所示,萝用串联校正方式使校正后系统满足条件/ >50%则应采用()A.豁前较正迟后较正C.迟后超前较正D.用串麻檢正方式不可能满足梭正要求i 1(dB「D.满分:2分A.B.C.* D.满分:2分12.典型欠阻尼二阶系统,当幵环增益K 增加时, A.* B.C.D.满分:2分13.1型单位反馈系统的闭环增益为()* A.与幵环增益有关 单位反惯系统的开环传递函数®对= 16 5(S +4 其幅值裕度五等于(、 11. A. 0C. L€dB 系统()B.与传递函数的形式有关15. 盘O 一 3) ■ 7737+15 a +3r-F?y + lQ D* as +3应 T+sTTioA.B.C.D. 广C.1D. 与各环节的时间常数有关满分:2分幵环系统弘%图如图所示」对应的幵环传递匡嗷GO )应该是<)14.C.D.满分: 已知系痢环传色i 砂=芦时,讓谿係统根轨述则麟沏环传酒数应该是(>—+1D*—+110已知串联枝正装蚤的号递国数为兽g(> s + 10满分:2分若二阶系统处于元阳尼狀态,则系统的阻尼比£应为()A・。
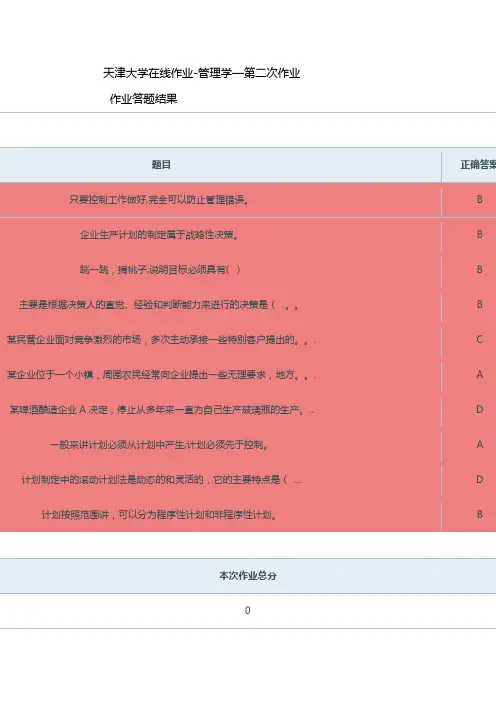
天津大学在线作业-管理学—第二次作业作业答题结果题目正确答案只要控制工作做好,完全可以防止管理错误。
B企业生产计划的制定属于战略性决策。
B跳一跳,摘桃子,说明目标必须具有( ) B 主要是根据决策人的直觉、经验和判断能力来进行的决策是( .。
B 某民营企业面对竞争激烈的市场,多次主动承接一些特别客户提出的。
. C 某企业位于一个小镇,周围农民经常向企业提出一些无理要求,地方。
. A 某啤酒酿造企业A决定,停止从多年来一直为自己生产玻璃瓶的生产。
.. D 一般来讲计划必须从计划中产生,计划必须先于控制。
A 计划制定中的滚动计划法是动态的和灵活的,它的主要特点是( ... D 计划按照范围讲,可以分为程序性计划和非程序性计划。
B本次作业总分作业答题结果题目正确答案比较优选原则主要是指任何决策都有利有弊,故决策者只能在利弊之... A 企业的具体环境中最主要的是: () A 应用头脑风暴法时,需要限制参与人发言以保证讨论围绕主题进行。
B 计划制定中的滚动计划法是动态的和灵活的,它的主要特点是( 。
D 经济学中所谓“资源是稀缺的”,这一说法隐含的深意是:( .。
C 决策拟定的方案越多越好. B 美国克莱斯勒汽车公司的总经理艾柯卡普曾经说过,“等到委员会讨.。
D 主要是根据决策人的直觉、经验和判断能力来进行的决策是( .。
B 某啤酒酿造企业A决定,停止从多年来一直为自己生产玻璃瓶的生产。
.. D 决策首先必须识别机会或是发现问题。
A本次作业总分作业答题结果题目正确答案企业生产计划的制定属于战略性决策。
B 行为决策学派认为决策是一个优选过程,所以决策结果是基于已有资。
. B 某民营企业面对竞争激烈的市场,多次主动承接一些特别客户提出的... C 一般来讲计划必须从计划中产生,计划必须先于控制。
A 国家宏观经济政策是构成企业以下哪种类型的要素之一?() C 计划制定中的滚动计划法是动态的和灵活的,它的主要特点是( .。
西交《自动控制理论》在线作业
试卷总分:100 得分:100
一、多选题(共13 道试题,共39 分)
1.相位超前校正具有以下特点()
A.系统带宽变窄,降低了系统响应的快速性
B.增益和型次未改变,稳态精度变化不大
C.加大带宽,加快了系统的响应速度,即改善系统的瞬态性能
D.增大相位裕度,提高了系统的相对稳定性
答案:BCD
2.属于代数稳定性判据的有()。
A.奈奎斯特判据
B.波德判据
C.胡尔维兹判据
D.劳斯判据
答案:CD
3.关于传递函数正确的说法有( )
A.传递函数的分母与系统的输入无关
B.传递函数分母中s的阶次不小于分子中s的阶次
C.传递函数是无量纲的
D.不同物理类型的系统,可以具有相同形式的传递函数。
自动控制原理随堂练习答案一、选择题1. 在自动控制系统中,用来感知被控对象状态的装置是( B )。
A. 电源B. 传感器C. 执行器D. 控制器答案:B. 传感器解析:传感器是自动控制系统中用来感知被控对象状态的装置,通过将被控对象的状态转化为电信号或者其他形式的信号,提供给控制器进行处理。
2. PID控制器中的P、I、D分别代表( C )。
A. 位置、速度、加速度B. 功率、电流、电压C. 比例、积分、微分D. 压力、温度、流量答案:C. 比例、积分、微分解析:PID控制器是一种常用的控制器,其中P代表比例控制,I代表积分控制,D代表微分控制。
这三个控制参数可以根据被控对象的特性进行调节,以实现控制系统的稳定性和响应速度的要求。
3. 在自动控制系统中,被控对象是指( D )。
A. 控制器B. 传感器C. 执行器D. 需要控制的物理系统答案:D. 需要控制的物理系统解析:被控对象是指需要通过控制器来控制的物理系统,例如温度控制系统中的温度传感器感知温度值,控制器根据温度值调节执行器控制加热或者制冷设备,以达到控制温度的目标。
4. 在自动控制系统中,控制器的作用是( B )。
A. 感知被控对象状态B. 根据反馈信号调节执行器C. 将被控对象状态转化为电信号 D. 提供电源给被控对象答案:B. 根据反馈信号调节执行器解析:控制器是自动控制系统中的核心部份,其作用是根据传感器反馈的信号,通过对执行器的调节,改变被控对象的状态,使其达到预定的目标状态。
5. 在自动控制系统中,负反馈的作用是( A )。
A. 提高系统的稳定性B. 提高系统的灵敏度C. 提高系统的响应速度D. 提高系统的抗干扰能力答案:A. 提高系统的稳定性解析:负反馈是自动控制系统中常用的控制策略,其作用是通过将被控对象的输出信号与期望输出进行比较,产生误差信号,然后根据误差信号来调节执行器,以减小误差,提高系统的稳定性。
二、填空题1. 自动控制系统的基本组成部份包括传感器、控制器和(执行器)。
现代控制理论第一次作业1-1.由图1-1所示,可得:1311322323313112121()331()122x u x s x u x x x u x x x u x s x x x x y x x u s y x x u⎧=-⎪+=--⎧⎪⎪⎪=--=-⎪⎪⇒+⎨⎨=⎪⎪=⎪⎪=++⎩⎪⎪=++⎩ 则状态空间可表示为:()301101112000110x x uy x u--⎛⎫⎛⎫⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=+ 1-4.由101,111A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭。
11210()()1110111(1)1s s sI A s s s s ---⎛⎫Φ=-= ⎪--⎝⎭⎛⎫ ⎪-⎪= ⎪ ⎪--⎝⎭则,110[()]t Attt e e L sI A tee --⎛⎫=-= ⎪⎝⎭, ()010()()1()t ttA t t t e eBu d u d t e e τττττττττ----⎛⎫⎛⎫=⎪ ⎪-⎝⎭⎝⎭⎰⎰,()1u τ= 则,()0()(0)()1010212tAtA t t t t t t t t x t e x e Bu d e e te e te e te τττ-=+⎛⎫⎛⎫-⎛⎫=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫-= ⎪⎝⎭⎰1-5.(1)极点多项式为: 由()2rank G s =, 一阶子式公分母:2(1)s s + 二阶子式公分母:22(1)s s + 极点多项式为:22(1)s s + (2)零点多项式为:二阶子式:2222212(1)()212(1)(1)s s s s s s s s --+-++=++ 零点多项式为:1(1)()2s s -+现代控制理论第二次作业1-7.系统的状态方程为:x Ax bu =+其中,01101001n A a a a -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥---⎣⎦,001b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦。
1101111101111011000()011**1001**111n n n n n n n n n s sI A b s s s s s s s s s s s ααααααααα----------⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥-⎢⎥⎢⎥+⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥++++⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥=⎢⎥++++⎢⎥⎣⎦1-8.反证法:设1121[]n rank b AbA b n n -=<,则存在一个非零向量α使得: 11111011[]00n n n bAbA b b Ab A b αααα---=+++=不防设110n α-≠,则,11111201211()n n n n A b b Ab A b αααα----=-+++两边同乘A ,则11111201211()n n n n A b Ab A b A b αααα---=-+++则可看出1n A b 能用12(,,)n b Ab A b -线性表出,以此类推,可得11+1n n n A b A b A b (,)均可由12(,,)n b Ab A b -线性表出,则:121[]n rank b AbA b n n -=≠ 与已知矛盾,假设不成立,所以有111[]n rank b AbA b n -=1-9.(1)解:010110001A ⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦,011b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,[]121C =可控性矩阵2011110111U bAbA b -⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥⎣⎦,det 0U ≠,故系统可控。
现代控制理论试卷作业一.图为R-L-C 电路,设u 为控制量,电感L 上的支路电流11121222121212010Y x U R R R R Y x R R R R R R ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦+++⎢⎥⎢⎥⎣⎦⎣⎦和电容C 上的电压2x 为状态变量,电容C 上的电压2x 为输出量,试求:网络的状态方程和输出方程(注意指明参考方向)。
解:此电路没有纯电容回路,也没有纯电感电路,因有两个储能元件,故有独立变量。
以电感L 上的电流和电容两端的电压为状态变量,即令:12,L c i x u x ==,由基尔霍夫电压定律可得电压方程为:从上述两式可解出1x ∙,2x ∙,即可得到状态空间表达式如下:⎥⎦⎤⎢⎣⎡21y y =⎥⎥⎦⎤⎢⎢⎣⎡++-211212110R R R R R R R ⎥⎦⎤⎢⎣⎡21x x +u R R R ⎥⎥⎦⎤⎢⎢⎣⎡+2120 二、考虑下列系统:(a )给出这个系统状态变量的实现;(b )可以选出参数K (或a )的某个值,使得这个实现或者丧失能控性,或者丧失能观性,或者同时消失。
解:(a )模拟结构图如下:则可得系统的状态空间表达式:(b ) 因为 3023A -⎡⎢=⎢⎢⎣ 0013 k k a -⎤⎥-⎥⎥-⎦ 110b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦所以:当1a =时,该系统不能控;当1a ≠时,该系统能控。
又因为:[2C = 1 ]0所以:当0k =或1a =时,该系统不能观;当0k ≠且1a ≠时,该系统能观。
综上可知:当1a =时或0k =且1a =时,该系统既不能控也不能观。
三、已知系统.Ax x =∙的状态转移矩阵为:(1)试确定矩阵A ,并验证At e 确为上式。
(2)已知A 求At e ,以下采用三种方法计算At e ,并对计算结果进行讨论。
解:(1)利用书上P53状态转移矩阵的性质四:对于状态转移矩阵,有A t t A t )()()(φφφ==∙ 即A e Ae e dtd At At At == 当t=0时 I =)0(φ I =-)0(1φ验证At e :(利用P59的公式(2-24)来验证)解得:221-==λλ,13-=λ,有一对复根,重根部分按公式(2-24)处理,非重根部分的i a 仍按公式(2-23)计算。
第三章3-1 已知二阶系统闭环传递函数为 369362++=s s G B 。
试求单位阶跃响应的t r , t m ,δ% , t s 的数值?解:[题意分析]这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n ω参数,而后把n ω代入性能指标公式中求出r t ,m t ,%δ,s t 和N 的数值。
)/(636秒弧度==n ω(弧度)秒(弧度72.041.411)/97.3166.0175.0292122=︒=-==-⋅==-==-ζζθζωωζωζtgn d n上升时间 t r 秒61.097.372.014.3=-=-=d r t ωθπ 峰值时间t m 秒79.097.314.3===d m t ωπ 过度过程时间t s %)2(89.0675.044秒=⨯==ns t ωζ%)5(70.0675.033秒=⨯==ns t ωζ超调量δ%%8.2%100%100%66.075.012=⨯=⨯=---πζπζδee3-2 设单位反馈系统的开环传递函数为 )1(1)(+=s s s G K试求系统的性能指标,峰值时间,超调量和调节时间。
解:[题意分析]这是一道给定了开环传递函数,求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数(ζ,n ω)的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为 11)()()(2++==s s s X s Y s G B 与二阶系统传递函数标准形式2222nn n s s ωζωω++相比较可得12,12==n n ζωω,即n ω=1,ζ=0.5。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为秒秒秒615.033%)5(815.044%)2(%4.16%100%63.31212=⨯===⨯===⨯==-⋅=--ns ns n m t t et ζωζωδζωπζπζ3-3 如图1所示系统,假设该系统在单位阶跃响应中的超调量%δ=25%,峰值时间m t =0.5秒,试确定K 和τ的值。
图1解:[题意分析]这是一道由性能指标反求参数的题目,关键是找出:K,τ与ζ,n ω的关系;%δ,m t 与ζ,n ω的关系;通过ζ,n ω把%δ,m t 与K,τ联系起来。
由系统结构图可得闭环传递函数为 Ks K s Ks K s s K s X s Y s G B +++=+++==)1()1()1()()()(2ττ 与二阶系统传递函数标准形式相比较,可得221212;nn n n K K ωζωττζωω-=+==或由题目给定: %25%100%21=⨯=--ζζπδe即 25.021=--ζζπe两边取自然对数可得 3863.125.0ln 12-==--ζπζ4.03863.13863.122=+=πζ依据给定的峰值时间: 5.012=-=ζωπn m t (秒)所以 85.615.02=-=ζπωn (弧度/秒)故可得4795.462≈==n K ωτ≈0.13-4 已知系统的结构图如图2所示,若)(12)(t t x ⨯= 时,试求:(1) 当τ=0时,系统的t r , t m , t s 的值。
(2) 当τ≠0时,若使δ%=20%,τ应为多大。
图2解:[题意分析]这是一道二阶系统综合练习题。
(1)练习输入信号不是单位阶跃信号时,求性能指标。
关键是求出 n ω,ζ,θ。
(2)的求法与例4-3-3相似。
(1) 由结构图可知闭环传递函数为 50250)()()(2++==s s s X s Y s G B 可得 )/(07.750秒弧度==n ω弧度43.195.811;14.02221=︒=-===-ζζθωζtgn由于ss X 2)(=输出的拉氏变换为 22222)(nn ns s Y ωζωω++⋅=则拉氏反变换为[]%)2(71.307.714.044%)5(78.207.714.03345.099.007.714.3124.099.007.743.114.31%64%100%100%)95.817sin(01.112)sin(112)(2299.044.01995.022秒秒秒秒=⨯===⨯===⨯=-==⨯-=-⋅-==⨯=⨯=︒+-=⎥⎥⎦⎤⎢⎢⎣⎡+⋅--=-----ns ns n m n r d tt t t t eet e t e t y n ζωζωζωπζωθπδθωζζζωζ(2) 当τ≠0时,闭环传递函数50)5.02(50)()()(2+++==s s s X s Y s G B τ )/(07.750秒弧度==n ω5.0)1(25.022-=+=n n ζωττζω得由 %20%100%21=⨯=--ζζπδe2.021=--ζζπe两边取自然对数 61.12.0ln 12-==--ζζπ, 可得46.061.161.122=+=πζ故 73.85.)107.746.0(2=-⨯=o τ%)2(92.007.746.033秒=⨯==ns t ζω3-5(1) 什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。
(2) 时间响应由哪几部份组成?各部份的定义是什么?答:时间响应由瞬态响应和稳态响应两部分组成。
瞬态响应是系统受到外加作用后,系统从初始状态到最终稳定状态的响应过程称瞬态响应或者动态响应或称过渡过程。
稳态响应是系统受到外加作用后,时间趋于无穷大时,系统的输出状态或称稳态。
(3) 系统的单位阶跃响应曲线各部分反映系统哪些方面的性能?答:时间响应由瞬态响应和稳态响应两部分组成。
瞬态响应反映系统的稳定性,相对稳定性及响应的快速性;稳态响应反映系统的准确性或稳态误差。
(4) 时域瞬态响应性能指标有哪些?它们反映系统哪些方面的性能?答:延迟时间d t ;上升时间r t ;峰值时间m t ;调节时间s t ;最大超调量%δ.d t ,r t ,m t ,s t 反映系统的快速性,即灵敏度,%δ反映系统的相对稳定性。
3-6设系统的特征方程式为 0611126234=++++s s s s试判别系统的稳定性。
解:特征方程符号相同,又不缺项,故满足稳定的必要条件。
列劳斯表判别。
36)61(0455)6(36610116612101234s s s s s 同乘同乘 由于第一列各数均为正数,故系统稳定。
也可将特征方程式因式分解为 0)1)(3)(2(2=++++s s s s根2321,3,24,321j s s s ±-=-=-=均有负实部,系统稳定。
3-7设系统的特征方程式为 02223=+++s s s解:列劳斯表212210123εs s s s将特征方程式因式分解为 0)2)(1(2=++s s根为 2,132,1-=±=s j s系统等幅振荡,所以系统临界稳定。
3-8 单位反馈系统的开环传递函数为 )125.0)(11.0()(++=s s s Ks G k试求k 的稳定范围。
解:系统的闭环特征方程: 035.0025.00)125.0)(11.0(23=+++=+++K s s s K s s s列劳斯表Ks K Ks Ks s 012302.035.035.01025.0-系统稳定的充分必要条件 K>00.35-0.025K>0得 K<14所以保证系统稳定,K 的取值范围为0<K<14。
3-9(1) 系统的稳定性定义是什么?答:系统受到外界扰动作用后,其输出偏离平衡状态,当扰动消失后,经过足够长的时间,若系统又恢复到原平衡状态,则系统是稳定的,反之系统不 稳定。
(2) 系统稳定的充分和必要条件是什么?答:系统的全部特征根都具有负实部,或系统传递函数的全部极点均位于[S]平面的左半部。
(3) 误差及稳态误差的定义是什么?答:输出端定义误差e(t):希望输出与实际输出之差。
输入端定义误差e(t);输入与主反馈信号之差。
稳态误差,误差函数e(t),当t →∞时的误差值称为稳态误差,即3-10已知单位反馈随动系统如图3所示。
若16=K ,s T 25.0=。
试求: (1)典型二阶系统的特征参数ζ和n ω; (2)暂态特性指标pM 和)5(00s t ;(3)欲使016=p M ,当T 不变时,K 应取何值。
图3随动系统结构图解: 由系统结构图可求出闭环系统的传递函数为T Ks T s TK K s Ts K s Φ++=++=1/)(22与典型二阶系统的传递函数比较 2222s (s)n n n s Φωζωω++=得KT T K n 21,==ζω已知K 、T 值,由上式可得25.021),/(825.016=====KT s rad TKn ζω于是,可%47%100%100%2225.0125.01=⨯=⨯=----πζζπe eM p)%5(5.1825.033=∆=⨯=≈s t ns ζω为使016=p M ,由公式可求得5.0=ζ,即应使ζ由0.25增大到0.5,此时425.025.04141=⨯⨯=≈ζT K 即K 值应减小4倍。
3-11控制系统框图如图4所示。
要求系统单位阶跃响应的超调量%5.9=p M ,且峰值时间st p 5.0=。
试确定1K 与τ的值,并计算在此情况下系统上升时间r t 和调整时间)2(00s t 。
图4 控制系统框图解:由图可得控制系统的闭环传递函数为:12110)101(10)()(K s s K s R s C +++=τ系统的特征方程为010)101(12=+++K s s τ。
所以τξωω1012,1021+==n n K 由题设条件:095.0%10021=⨯=--ξξπeM p ,st n p 5.012=-=ξωπ可解得854.7,6.0==n ωξ,进而求得84.01012,15.61021=-===n nK ζωτω 在此情况下系统上升时间radst n r 9273.01.53)(cos 35.01012====--=-ζθζωθπ调整时间85.04%)2(=≈ns t ζω3-12设系统的特征方程式分别为1.05432234=++++s s s s 2.0122234=++++s s s s 3.022332345=+++++s s s s s试用劳斯稳定判据判断系统的稳定性。
解:解题的关键是如何正确列出劳斯表,然后利用劳斯表第一列系数判断稳定性。
1.列劳斯表如下s4 1 3 5 s3 2 4 s2 1 5 s1 -6 s0 5劳斯表中第一列系数中出现负数,所以系统不稳定;又由于第一列系数的符号改变两次,1→-6→5,所以系统有两个根在s 平面的右半平面。