字母表示数计算顺序

用字母表示数书写时注意6点
用字母表示数书写时，需要注意以下6点：
1．字母与字母相乘时，可省去乘号，并注意均数的单位名称是否消失。

2．乘方时，指数写在底数的右上角，并且字母与字母相乘时，可省去乘号，并注意均数的单位名称是否消失。

3．代数式中出现的乘方，一般改写为指数形式，用幂的形式表示。

4．用字母表示数的代数式中，含有加、减、除运算时，最后的结果通常用括号括起来。

5．用字母表示数的代数式中，要注意代数式意义的说明。

6．用字母表示数的代数式，一般写成立方、平方、立方或几次方和的形式；含有分数或根号的字母周围的数字和根号根据需要进行分节。

1、常用的长度单位：千米：km 米：m 分米：dm 厘米：cm 毫米：mm2、常用的面积单位;平方千米:k㎡平方米：㎡平方分米：d㎡平方厘米：c㎡3、重量单位吨:t 千克：kg 克：g运算定律：1、两个数相加，交换加数的位置，它们的和不变。

用字母表示为：a + b=b + a加法结合律：三个数相加，先把前两个数相加，再把第三个数相加，或者先把后两个数相加，再同第一个数相加，它们的和不变。

用字母表示为：（a+b）+c=a+（b+c）3、乘法交换律：两个数相乘，交换因数的位置，它们的积不变。

用字母表示为：a×b=b×a4、乘法结合律：三个数相乘，先把前两个数相乘，再同第三个数相乘，或者先把后两个数相乘，再同第一个数相乘，它们的积不变。

用字母表示为：（a×b）×c=a×（b×c）5、乘法分配律：两个数的和同一个数相乘，可以把这两个数分别同这个数相乘，再把所得的积加起来，结果不变。

用字母表示为：（a + b）×c=a×c + b×c6、在含有字母的式子里，乘号可以记作小圆点，也可以省略不写。

如：X×2或2×X都可以记作2·X或2X，但要注意在省略乘号的时候要把数写在字母的前面。

7、1与任何字母相乘时，1可以省略不写，如1×b，或b×1，都可以记作b。

8、字母和字母相乘，中间的乘号也可以记作小圆点，或省略不写。

如a×b，记作a·b或ab。

两个相同的字母相乘，如b×b，可以记作b ，读作b的平方。

9、只有字母与字母之间、数字与字母之间的乘号才能省略不写。

在省略乘号时，应当把数字写在字母前面。

10、几点说明：（1）a×2＝2×a＝2a （2）a×b = a b = a b（3）数与数相乘时用“×”号。

（4）和式中出现单位需加括号。

用字母表示数的书写要求(一)用字母表示数的书写1. 引言在数学和科学领域中，为了方便表达和计算，人们经常使用字母来表示数字。

这种书写方式可以简化复杂的数值运算，并提供了更灵活的表达能力。

本文将阐述用字母表示数的书写的相关要求，并通过举例解释说明。

2. 相关要求字母与数字的对应关系在用字母表示数的书写中，每个字母都与一个特定的数字相对应。

这种对应关系可以是一一映射的，也可以是多对一映射的。

不同的领域和应用中，可能会有不同的字母与数字对应规则。

大写与小写字母的使用通常情况下，大写字母用于表示常数或不变量，小写字母用于表示变量。

这样的规则更容易区分字母所代表的含义，增加了书写的清晰度和可读性。

表达式的书写顺序用字母表示数的书写时，通常按照从左到右的顺序书写，和传统的数学表达式书写方式一致。

这种书写顺序可以减少歧义，并使表达更加准确和简洁。

3. 举例解释数学公式中的字母表示数在数学领域中，用字母表示数的书写是非常常见的。

例如，著名的质能方程E=mc²中的字母E代表能量，m代表物体的质量，c代表光速。

这种书写方式使得质能方程更加简洁明了，方便进一步的计算和研究。

编程语言中的字母表示数在编程语言中，常常使用字母表示数来定义变量和存储数据。

例如，在Python中，可以用字母x表示一个整数，而字母y表示一个浮点数。

这样的书写方式使得程序的逻辑更加清晰，并且方便变量的调用和赋值。

物理学中的字母表示数在物理学中，用字母表示数的书写是必不可少的。

例如，力学中的运动方程s=vt中，字母s代表位移，v代表速度，t代表时间。

这种书写方式可以简化运动方程的表达，从而更方便地分析和计算物理现象。

结论用字母表示数的书写在数学、科学和编程等领域中扮演着重要的角色。

了解相关要求，并灵活运用这种书写方式，可以提高表达和计算的效率，使问题更加清晰明了。

希望本文对读者有所帮助，并激发更多关于用字母表示数的探讨和应用。

第二单元《用字母表示数》知识点背诵1.在数学教学中，我们经常用字母表示（数），用含有字母的式子表示（数量关系或计算公式）。

2.通常用t表示时间，t分钟的节水量表示为10×t。

3.在含有字母的式子中，字母和字母、字母和数字之间的乘号（“×”）可以记作“∙”或省略不写，并且数字在前，字母在后。

如：10×t可以写作：10t。

一般字母与字母相乘按照英文字母的排序决定简写顺序，如：a×b写作：ab。

（总结：数字在前、字母在后，乘号省略）代数式中的“+”“-”“÷”不能省略不写。

4.在用含有“+”“-”“÷”的代数式表示结果需要加单位时，需要把整个代数式加“（）”。

例如：（3m+5）元、（n÷4）个。

5.求含有字母式子的值（也就是代入求值）：先写出含有字母的式子，然后将式子中所有字母换成所取的值进行计算，最终计算结果后不加单位！！写答的时候要加上单位，和以前写答一样。

例如：当a=4时，3a+6 先写原始的代数式=3×4+6脱式计算，等号对齐=18 （这里没有单位！）答：小明花了18元。

如果代数式中有两个及以上字母，要分别把数值带入替换对应的字母正确求值。

如：当a=2,m=4时，3a + 2m=3×2+2×4=146.在数学上，我们通常用字母s表示路程，v表示速度，t表示时间；路程=速度×时间，用含有字母的式子表示为：s=v×t或s=vt速度=路程÷时间，用含有字母的式子表示为：v=s÷t时间=路程÷速度，用含有字母的式子表示为：t=s÷v已知其中两个量可以求第三个，如：甲车行驶的速度为60米/分，若t=5,那么甲车走了多远？（此题已知速度和时间，求路程，所以用到：s=v×t这个关系式）当t=5时，代入求值：s=v×t=60×5 注意格式和单位（没有单位） =300答：甲车5分钟走了300米。

用字母表示数书写时注意6点
摘要：
1.字母表示数的概念和用途
2.书写时需要注意的6个要点
3.总结与建议
正文：
字母表示数是数学中的一种表示方法，尤其在代数中应用广泛。

通过字母表示数，可以更方便地表示和解决数学问题。

但在书写过程中，我们需要注意以下6点：
1.字母选择：尽量选择容易理解的字母，如a、b、c等，避免使用易混淆的字母，如x、y、z等。

2.字母顺序：遵循字母表的顺序，从a开始，按顺序排列。

如果需要表示多个数，可以继续使用字母表中的字母，如a、b、c、d等。

3.指数表示：当需要表示一个数的幂时，可以在字母后面加上指数，如
a、b等。

注意，指数应使用阿拉伯数字表示。

4.乘法表示：在表示乘法时，应使用“·”或“*”符号。

例如，a·b或a*b 表示a与b的乘积。

5.除法表示：在表示除法时，应使用斜杠“/”符号。

例如，a/b表示a除以b。

6.分数线表示：在表示带分数时，应使用分数线“/”符号。

例如，a/b表示a除以b的商，a/(b+c)表示a除以b与c的和。

总之，在书写字母表示数的数学问题时，我们需要注意字母的选择、顺序、指数表示、乘法表示、除法表示以及分数线表示这6个方面。

四年级数学下册知识结构总结用字母表示数一、用字母表示数的格式（默写）1、用字母表示数：在含有字母的式子里，数字和字母、字母和字母中间的乘号可以记作“.”，也可以省略不写。

省略时，通常把数字写在字母前面。

如：5×a x×3 a×x x×y×6 1×b 7×7 a×b a×b×c （a—b）÷3写为：5a 3x ax 6xy b 7•7 ab abc a/3－b/3或1/3(a－b)2、求含有字母的式子的值时要注意格式：首先写出字母等于几，再写出含有字母的式子，然后利用脱式计算的形式，将字母换成数再计算即可。

例：超市原有b台彩电，卖出70台后，超市还有彩电（b—70）台。

当b=150台时，超市还有彩电：b—70=150—70=80（台）二、用字母表示数量关系，1、表示路程公式：s=vt；（默写）例：一辆汽车，每小时行驶a千米，上午行驶了4小时，下午行驶了b千米，这辆汽车共行驶了（4a+b）千米。

当a=80 b=200时，这辆汽车行驶了：4a+b=4×80+200=520（千米）。

2、含字母的式子比较大小：如: “< = ˃”2Χ一定（）Χ²。

1）大于2）小于3）等于4）不能确定注意：a²和2a，当a=2时，其值相等；当a≠2时，无法确定。

3、表示面积、周长公式:（默写）正方形的面积公式：s=a•a 或s=a²长方形的面积：S=ab正方形的周长：C=4a长方形的周长：C=2•(a+b) 或c=2(a+b)4、应用类：①某班有女生X人，女生比男生少8人，则某班全体同学的人数是（2X+8）人。

如果X=23时，则某班人数为2x+8=46+8=54（人）②青青林场栽了梧桐树和雪松各X排，已知梧桐树每排12棵，雪松树每排14棵，栽梧桐树和雪松树共计（12+14）X棵。

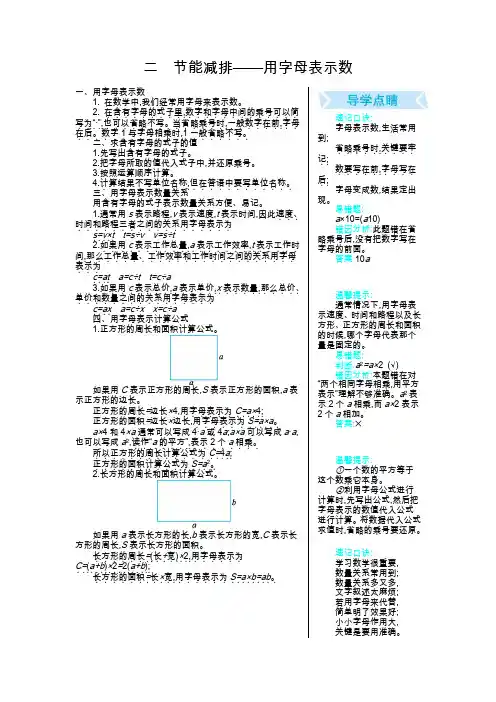
二 节能减排——用字母表示数一、用字母表示数1. 在数学中,我们经常用字母来表示数。

2. 在含有字母的式子里．．．．．．．．．,．数字和字母中间的乘号可以简．．．．．．．．．．．．．写为“．．．·”．,．也可以省略不写。

当省略乘号时．．．．．．．．．．．．．．,．一般数字在前．．．．．．,．字母．．在后。

数字．．．．．1．与字母相乘时．．．．．．,．1．一般省略不写。

．．．．．．．二、求含有字母的式子的值 1.先写出含有字母的式子。

2.把字母所取的值代入式子中,并还原乘号。

3.按照运算顺序计算。

4.计算结果不写单位名称．．．．．．．．．．,．但在答语中要写单位名称。

．．．．．．．．．．．． 三、用字母表示数量关系用含有字母的式子表示数量关系方便、易记。

1.通常用s 表示路程,v 表示速度,t 表示时间,因此速度、．．．时间和路程三者之间的关系用字母表示为．．．．．．．．．．．．．．．．．．s=v×t ．．．．． t=s÷v v=s÷t 2.如果用．．．c ．表示工作总量．．．．．．,．a ．表示工作效率．．．．．．,．t ．表示工作时．．．．．间．,．那么工作总量、工作效率和工作时间之间的关系用字母．．．．．．．．．．．．．．．．．．．．．．．．表示为．．．c=at ．．．． a=c÷t t=c÷a 3.如果用．．．c ．表示总价．．．．,．a ．表示单价．．．．,．x ．表示数量．．．．,．那么总价、．．．．．单价和数量之间的关系用字母表示为．．．．．．．．．．．．．．．．c=ax ．．．．a=c÷x x=c÷a 四、用字母表示计算公式1.正方形的周长和面积计算公式。

如果用C 表示正方形的周长,S 表示正方形的面积,a 表示正方形的边长。

正方形的周长=边长×4,用字母表示为．．．．．．C=a×．．．．4．;． 正方形的面积=边长×边长,用字母表示为．．．．．．S=a×a ．．．．．。

数学符号运算优先级
数学符号运算优先级通常是指在进行算术运算时的规则顺序。

对于大部分算术表达式，运算的顺序是从左到右。

但当一个算式中有多种运算符时，我们必须先计算优先级高的运算符。

以下是常见的数学运算符及其优先级（从高到低）：
1.括号：括号内的运算总是优先于括号外的运算。

例如，(a+b)*c 先
计算括号内的a+b。

2.指数运算符：如^、** 或pow(a, b) 表示a 指数为b。

例如，
2^3 或pow(2, 3) 等于8。

3.乘法、除法和取余：包括*、/ 和%。

例如，在表达式a*b+c/d 中，
先计算a*b 和c/d。

4.加法和减法：包括+ 和-。

例如，在表达式a+b-c*d 中，先计算
c*d。

5.一元运算符：如-a 或+a。

这些在一元运算符之后进行。

6.比较运算符：如==, !=, <, >, <=, >=。

这些通常用于比较和条件表
达式中，优先级较低。

但要注意的是，虽然以上规则提供了一个通用的运算优先级顺序，但在实际数学或编程中，有时候会使用括号来明确指定运算的顺序，以确保得到预期的结果。

括号可以改变默认的运算顺序。

用字母表示数的书写要求在现代社会中，我们经常需要使用字母来表示数字。

无论是在数学、科学、计算机科学还是日常生活中，字母表示数都是非常常见和重要的技能。

在本文中，我将为您介绍如何正确地使用字母来表示数，并提供一些书写要求。

让我们来看一下如何使用字母表示整数。

在英语中，我们使用26个字母来表示数字。

例如，字母"A"表示1，字母"B"表示2，以此类推，字母"Z"表示26。

如果我们需要表示一个大于26的整数，我们可以将字母按照字母表的顺序重复使用。

例如，27可以表示为"AA"，28可以表示为"AB"，依此类推。

对于更大的整数，我们可以使用更多的字母组合来表示。

当然，在使用字母表示数字时，我们需要遵循一些书写规范。

首先，我们应该确保在文章中不插入任何网络地址（http）。

这是为了避免文章中出现无关的链接，保持文章的纯粹性和流畅性。

我们在文章中不得包含数学公式或计算公式。

这是为了保持文章的简洁性和易读性。

如果需要进行数学计算，可以使用文字描述或者使用具体的数字来代替公式。

我们需要确保文章内容的独一性，避免内容重复出现。

这样可以增强文章的阅读体验，避免读者感到枯燥和重复。

为了使文章结构合理，段落明晰，我们需要使用适当的标题来组织内容。

标题可以帮助读者更好地理解文章的结构和内容，提高阅读的流畅性。

在文章中，我们不应该插入任何形式的图片链接。

这是为了避免文章的复杂性和混乱性。

如果需要插入图片，可以使用文字描述或者提供具体的示例来说明。

我们也应该避免使用依赖图像的语句，如“如图所示”等字眼。

这样可以使文章更加自然和流畅，避免给读者带来困惑。

在文章中，我们应该避免反复提出同一个问题。

这样可以使文章更加简洁和清晰。

如果需要解决多个问题，可以使用适当的分段和标题来组织内容。

我们也不需要在文章中过多自我介绍。

文章的重点应该放在如何正确地使用字母来表示数字上，而不是个人经历或背景。

字母表示数、代数式一．字母表示数1、用字母表示数的意义和作用用字母表示数，可以把数量关系简明的表达出来，同时也可以表示运算的结果。

如：（1）加法交换律：a b b a +=+ （2）加法结合律：()()a b c a b c ++=++ （3）乘法交换律：ab ba = （4）乘法结合律：()()ab c a bc = （5）分配律：()a b c ab ac +=+2、用字母表示数的要求： 1．省略上的要求字母和数，字母和字母相乘时，可不写“× ”号，用“• ”表示，也可以什么符号都不写，直接把数或字母写在一起。

例如， a ×b ×c 可写成 a •b •c 或 abc7x y ⨯⨯可写成7x y ⋅⋅或7xy 。

字母和1相乘时，可不写1。

例如， 1×a 就写成a ， 1×b 就写成b 。

2．顺序上的要求字母和数相乘时，省略乘号，必须把数写在字母的前面。

例如，5a ⨯要写成5a ⋅或5a ，不能写成a5 。

字母和字母相乘时，习惯上按英文字母顺序写（不是必须这样写）。

例如：x a ⨯ 一般写成ax ，3b a ⨯⨯一般写成3ab 。

3．写法上的要求相同的字母相乘，要写成乘方的形式。

例如，a a ⨯ 写成 2a ，x x x ⨯⨯写成3x ，()()a b a b -⨯-写成()2a b -。

带分数与字母相乘，省略乘号后，要将带分数化为假分数。

例如，112a ⨯写成32a ，而不能写成112a 。

4．单位名称上的要求用含有字母的代数式表示一个数量时，要在最后写上单位名称，如果代数式是数与字母相乘的形式，不必用括号把代数式括起来；如果代数式有加减关系，要把代数式用括号括起来，再在括号外边写上单位名称。

例如，每千克苹果 a 元，买8千克应付8a 元。

这里的8a 不用括号。

一大箱苹果 a 千克，一小箱苹果 b 千克，4大箱苹果比3小箱苹果多()43a b - 千克。

用字母表示数板书一、用字母表示数的意义在数学中，用字母表示数是一个非常重要的工具，它可以帮助我们更简洁、更清晰地表达数学概念和规律。

用字母表示数可以让我们从具体的数字转移到更为一般和抽象的符号，从而更好地理解数学的本质。

二、用字母表示数的实例1. 加法交换律：a+b=b+a解释：通过用字母a和b表示两个数，我们可以清楚地看到加法交换律的规律。

这个规律表明，两个数的和与这两个数的顺序无关。

2. 减法结合律：-a=a+(-a)=(-a)+(-a)=-(a-a)=0解释：通过用字母a表示一个数，我们可以看到减法结合律的规律。

这个规律表明，减法运算满足结合律，即可以先减后面的数，再减前面的数。

3. 代数方程：ax=b的解解释：用字母a表示未知数x，并给出方程ax=b，我们可以求出x的值，即方程的解。

三、用字母表示数的应用1. 代数式：如2x+3y，x2+y2等。

2. 函数：如y=x+5，f(x)=x2等。

3. 几何中的点、线、面可以用字母表示，如点A、B，直线AB 等。

4. 代数方程、不等式、函数等都可以用字母表示，从而更好地研究和解决问题。

四、用字母表示数的注意事项1. 明确表示符号的含义：在用字母表示数时，要明确表示符号的含义，不要混淆符号和数字的意义。

2. 避免混淆符号的顺序：在用多个不同的符号表示同一个数时，要避免混淆符号的顺序，以免引起误解。

3. 注意符号的运算规则：在用字母表示数时，要遵守相应的符号运算规则，以便正确求解代数式或函数。

4. 正确求解方程的解：在用字母表示数时，要正确求解方程的解，以便得到正确的结果。

总之，用字母表示数是一种重要的数学工具，它可以帮助我们更简洁、更清晰地表达数学概念和规律。

通过明确表示符号的含义、避免混淆符号的顺序、遵守符号运算规则和正确求解方程的解，我们可以更好地运用这一工具解决数学问题。

五、例题解析例题：解方程3x+2=5x-1解析：将方程中的未知数x用字母a表示，得到3a+2=5a-1，解得a=3。

用字母表示数的格式
用字母表示数需要遵循一定的格式和规则，以确保数学表达的准确性和规范性。

以下是用字母表示数的基本格式和注意事项：
1.变量命名：通常使用小写字母来表示变量，例如a、b、c 等。

如果
需要表示多个变量，可以使用下划线或连字符来连接，例如a_1、b_2、c_x 等。

2.代数表达式：用字母表示数时，通常会使用代数表达式来表示数学关
系。

例如，如果需要表示两个数的和，可以写成 a + b 的形式。

3.幂运算：当需要表示数的幂时，应该使用指数表示法。

例如，a^2 表
示a 的平方，2^3 表示2 的三次方。

4.单位：在用字母表示数时，如果涉及到单位，应该明确指出单位。

例
如，速度v = 10m/s，其中m 表示米，s 表示秒。

5.变量范围：如果变量的取值范围有限制，应该在使用字母表示数时指
明。

例如，在概率论中，p 表示概率，取值范围为0 <= p <= 1。

6.符号约定：对于一些常用的符号或缩写，应该遵循数学界的约定。

例
如，π 表示圆周率，e 表示自然对数的底数等。

7.方程式：在用字母表示数时，方程式的书写也非常重要。

应该确保方
程式的左右两边平衡，并且等号两边对应的项具有相同的数学意义。

8.代数运算：在用字母表示数进行代数运算时，应该遵循代数的基本法
则和运算顺序。

例如，先乘除后加减，括号内的运算优先等。

总之，用字母表示数需要注意数学表达的准确性和规范性，遵循代数的基本规则和符号约定。

正确的格式和书写方式有助于提高数学表达的清晰度和可读性。

用字母表示数书写时注意6点摘要：一、引言二、用字母表示数的基本概念三、书写时需要注意的六点四、总结正文：一、引言在数学中，我们经常使用字母来表示数，这样可以简化表达式，使问题更加清晰易懂。

然而，在用字母表示数的过程中，有些细节需要我们注意，这将帮助我们更准确地表达数学概念。

本文将介绍用字母表示数时需要注意的六个要点。

二、用字母表示数的基本概念用字母表示数，就是用字母来代替数字，表示数的一种方法。

常见的表示方法有：a+b、a-b、ab 等。

在代数学中，字母通常用于表示未知数，而在其他数学领域，字母也可以表示已知数。

三、书写时需要注意的六点1.区分大小写：在代数学中，字母通常表示未知数，而数字则表示已知数。

为了区分大小写，通常将未知数用小写字母表示，已知数用大写字母表示。

2.不要使用模糊的字母：在表示数时，应尽量避免使用容易混淆的字母，如i、j、l 等。

可以使用较为清晰的字母，如a、b、c 等。

3.不要使用特殊符号：在表示数时，应尽量避免使用特殊符号，如@、#、$等。

这些符号可能会引起歧义，影响表达的准确性。

4.保持简洁：在表示数时，应尽量保持简洁。

避免使用过于复杂的表达式，以免增加理解难度。

5.注意运算顺序：在表示数时，应清楚地表示出运算顺序。

例如，a+b 表示先加a，再加b；而a-b 表示先减b，再减a。

6.遵循数学公式的书写规范：在表示数时，应遵循数学公式的书写规范。

例如，乘法应使用乘号×，除法应使用除号÷或分数线。

四、总结总之，在用字母表示数时，我们需要注意以上六个要点。

字母表示数计算顺序字母表示数计算顺序是指使用英文字母来表示数字，从而更容易进行数学计算的一种方式。

这种技术可以被用来帮助计算机编程，也可以帮助人们更轻松地进行简单的计算。

字母表示数计算顺序有助于我们更好理解数学思想并有助于儿童的数学学习。

使用字母表示数学计算的方式主要有三种：斯特灵数学（Stern-Brocot Mathematics）、拉斯维加斯模式（Las Vegas Model）以及古希腊数学（Greek Mathematics）。

斯特灵数学是一种简单的数学模式，它使用字母表示数字，例如A、B、C或D来表示1、2、3或4等数字。

斯特灵数学的基本原理是把不同的字母代表不同的数字，并可以运用英文字母组合进行数学计算。

这种方法促进了孩子们学习数学基础知识，能让他们更好地理解数学概念，并能够熟练运用英文字母进行数学计算。

拉斯维加斯模式也是一种使用字母表示数字计算的方式，它使用英文字母来表示大小为1~10的数字。

计算机以及数学家都熟悉这种表达大小为1~10的数学技术。

拉斯维加斯模式的优势在于它可以把不同的数字表达成不同的字母，以此降低计算的难度，帮助计算机和科学家计算更复杂的数学问题。

古希腊数学也被用于表示数字的计算，它使用字母和符号来表示数字，例如α（alpha）、β（beta）、Γ（gamma）等。

古希腊数学技术使用古希腊字母表示数字，使用不同的符号来表示不同的数字，从而实现快速简单的数学计算。

同时，这种方式还能激发孩子们对古希腊文化的兴趣，随着学习的深入，可以帮助建立孩子的数学思维。

通过分析可以看出，字母表示数计算顺序可以帮助人们更容易理解数学概念，使用字母表示也有助于激发孩子们对数学学习的兴趣。

学习这种方式能够丰富孩子们的科学素养和数学思维，使他们在学习过程中更容易理解数学概念，甚至可以帮助计算机编程。

另外，掌握字母表示数计算顺序能够培养孩子们对不同文化的认识，同时也能帮助他们更好地理解数学问题。

一些字母表示数的知识点一、用字母表示数的意义。

1. 概括性。

- 用字母表示数可以把数量关系简明地表示出来。

例如，在行程问题中，如果速度用v表示，时间用t表示，路程用s表示，那么路程s = vt。

这个式子可以概括所有速度、时间和路程之间的关系，不管速度和时间具体是多少数值，都可以用这个式子来计算路程。

2. 普遍性。

- 用字母表示数具有普遍性。

比如在表示加法交换律时，用a + b=b + a，这里的a和b可以代表任意的数，无论是整数、小数还是分数等，这个规律都成立。

二、用字母表示数的书写规则。

1. 数字与字母相乘。

- 数字与字母相乘时，数字在前，字母在后，乘号可以省略不写。

例如3× a 可以写成3a。

- 如果数字是1，1与字母相乘时，1省略不写，如1× b = b。

2. 字母与字母相乘。

- 字母与字母相乘时，乘号可以省略。

例如a× b = ab。

3. 带分数与字母相乘。

- 带分数要化成假分数后再与字母相乘。

例如1(1)/(2)× a=(3)/(2)a，而不能写成1(1)/(2)a。

4. 除法表示。

- 用字母表示除法时，一般写成分数形式。

例如a÷b=(a)/(b)(b≠0)。

三、求代数式的值。

1. 定义。

- 用数值代替代数式里的字母，按照代数式中的运算关系计算得出的结果叫做代数式的值。

例如，代数式2x + 3，当x = 5时，把x = 5代入代数式得2×5+3 = 10 + 3=13，13就是当x = 5时这个代数式的值。

2. 注意事项。

- 在代入求值时，要注意原来代数式中的运算顺序。

如果代数式中有括号，先算括号里面的。

例如，对于代数式(a + b)÷2，当a = 3，b = 5时，先计算a + b = 3+5 = 8，再计算8÷2 = 4。

所有用字母表示数的加法结合律和加法交换律在数学中，加法是最基本的运算之一。

我们通常使用数字来表示加法，但是在某些情况下，我们也会使用字母来表示数。

在这篇文章中，我们将探讨所有用字母表示数的加法结合律和加法交换律。

一、加法结合律加法结合律是指，当我们对三个或更多的数进行加法运算时，无论我们以什么顺序进行加法运算，得到的结果都是相同的。

例如，对于三个数a、b和c，我们可以按照以下两种方式进行加法运算：(a + b) + ca + (b + c)无论我们选择哪种方式，最终的结果都是相同的。

这就是加法结合律。

二、加法交换律加法交换律是指，当我们对两个数进行加法运算时，无论我们以什么顺序进行加法运算，得到的结果都是相同的。

例如，对于两个数a和b，我们可以按照以下两种方式进行加法运算：a + b无论我们选择哪种方式，最终的结果都是相同的。

这就是加法交换律。

三、应用举例现在，我们来看一些具体的例子，以更好地理解加法结合律和加法交换律。

例1：对于三个数a、b和c，我们可以按照以下两种方式进行加法运算：(a + b) + ca + (b + c)无论我们选择哪种方式，最终的结果都是相同的。

例如，当a=2，b=3，c=4时，我们可以得到以下结果：(2 + 3) + 4 = 92 + (3 + 4) = 9例2：对于两个数a和b，我们可以按照以下两种方式进行加法运算：a + b无论我们选择哪种方式，最终的结果都是相同的。

例如，当a=5，b=7时，我们可以得到以下结果：5 + 7 = 127 + 5 = 12四、总结在数学中，加法结合律和加法交换律是非常基本的概念。

它们不仅适用于数字，也适用于字母表示的数。

加法结合律告诉我们，无论我们以什么顺序进行加法运算，得到的结果都是相同的。

加法交换律告诉我们，无论我们以什么顺序进行加法运算，得到的结果都是相同的。

这些概念在数学中有着广泛的应用，对于我们理解和解决各种数学问题都非常重要。

用字母表示数的书写要求用字母表示数的书写是一种特殊的表示方式，它将数字用字母来代替，从而形成一种独特的数学表达方式。

这种书写方式在某些场合下非常有用，比如在密码学、计算机科学、代数等领域中经常会用到。

在用字母表示数的书写中，我们通常使用26个英文字母来代表数字，即A表示1，B表示2，依此类推，Z表示26。

这种书写方式可以使数字更加简洁、便于计算和理解。

在用字母表示数的书写中，我们需要遵守一些规定。

首先，字母的大小写可以有所区别，大写字母表示正数，小写字母表示负数。

例如，A表示正1，而a表示负1。

其次，字母的顺序表示数的大小，即字母越靠前，所表示的数越大。

比如，B表示2，而C表示3，所以B小于C。

此外，我们还可以使用字母的组合来表示更大的数，比如AB表示27，BC表示29，依此类推。

用字母表示数的书写有很多优点。

首先，它可以使数字更加简洁，减少书写的复杂性。

其次，它可以减少数字在传输和存储过程中的错误率，因为字母的识别和处理相对较为容易。

此外，用字母表示数的书写还可以在一定程度上保护数字的隐私性，因为只有了解规则的人才能够理解所表示的具体数值。

在实际应用中，用字母表示数的书写方式有很多具体的用途。

比如，在密码学中，我们可以通过将字母转换为数字来进行加密和解密操作。

在计算机科学中，我们可以使用字母来表示不同的变量和常量，从而简化程序的编写和理解。

在代数中，我们可以使用字母来表示未知数和系数，从而解决方程和求解问题。

用字母表示数的书写方式是一种独特而有用的数学表达方式。

它可以简化数字的书写和理解过程，减少错误率，并在许多领域中发挥重要作用。

虽然这种书写方式需要遵循一些规定，但一旦掌握了规则，就可以轻松地进行转换和计算。

希望通过本文的介绍，大家对用字母表示数的书写方式有了更加清晰的认识。